例談高中數學中數列遞推問題的處理方法
◇ 安徽 黃振東
數列是高中數學的重要知識點,但學生遇到較為復雜的遞推問題時,常常不知道如何下手,失分率較高.為避免這一情況的發生,教學中應注重篩選經典的例題,為學生講解數列遞推問題的處理方法,使學生掌握相關的解題技巧,實現快速解題.
1 新定義遞推問題
這類問題在高考中經常出現,主要考查學生的分析應用能力.解題時應深入理解題干,根據要求解的問題靈活應用數列通項公式的遞推方法.
例1設數列{an}滿足a1=2,an+1=an+2(n+1),若[x]表示不超過x 的最大整數(如[1.6]=1,[-1.6]=-2),則
A.2020 B.2019 C.2018 D.2017
解析
由已知條件an+1=an+2(n+1),可推出an+1-an=2(n+1),又因為a1=2,則an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=2n+2(n-1)+2(n-2)+…+4+2=n(n+1),則因此=2+1+1+…+1=2019,故選B.
2 奇偶項通項公式不同問題
高中數列問題中有一部分數列奇偶項的通項公式不同,問題難度較大.解答時需要進行分類,找到奇數項與偶數項之間的關系,再正確求解奇數項與偶數項的通項公式.
例2已知數列{an}的前n 項和Sn滿足Sn-則S100=( ).
解析
很多學生看到該題不知如何下手.事實上在突破該類問題時仍然需要應用所學的基礎知識,找到奇數項與偶項數之間的遞歸關系.
因為數列{an}的前n 項和Sn滿足
當n≥2時,得
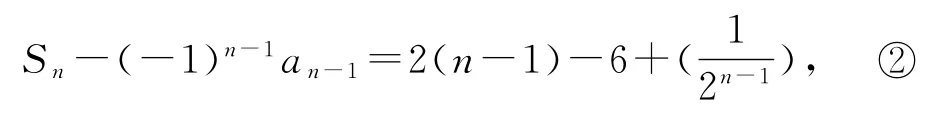
①-②得an-(-1)nan+(-1)n-1an-1=2-,所以當n 為偶數 時即n=102時,當n 為奇數時101時,2a101+a100=,因此,,即S100=a100+200-6+=200,故選B.
3 兩個數列問題
高中數列的部分習題涉及兩個數列,解答該類問題有時需要求解出其中一個數列的通項公式,有時則需要找到兩個數列之間的關系.
例3已知數列{an}滿足a1==+3an+1,若,設數列{bn}的前n 項和為Sn,則使得|S2019-k|最小的整數k 的值為( ).
A.0 B.1 C.2 D.3
解析
由an+1=an2+3an+1,可得an+1-an=+2an+1=(an+1)2≥0,故數列{an}為遞增數列,而an+1+1=+3an+2=(an+1)(an+2),因 此,,則,則
高中數列遞推問題難度較大,教學中教師應注重篩選經典例題,為學生深入細致地講解,同時組織學生開展相關的訓練活動,使學生真正地掌握相關的解題技巧,提升學習能力.

