例析高中數學函數解題思路的多元化
◇ 山東 伊淑橋
1 直接觀察法(定義域法)
例1求解函數的定義域及值域.
解析
由此推出函數的值域為[3,+∞).
點評
針對較為簡單的函數類問題,根據題目所給條件,利用觀察法我們就可以快速地分析出此題重點考查學生算術平方根的性質,隨后再根據算術平方根的性質即可正確解題.
2 函數單調性法
例2求解函數f(x)=3ln的定義域及值域.
解析
點評判斷函數的單調性有多種方法,學生可以使用定義法直接判斷所給函數在給定區間是否單調,同時還可利用復合函數分析法,由“同增異減”來確定函數單調性.另外,針對較為常見的函數,學生也可以利用圖象法來判斷函數的單調性.
3 反函數求解法
例3求解函數的值域.
解析
點評
反函數在高中階段并不常用,但教師在教學過程中要引導學生掌握一定的反函數基礎,為進一步的數學學習奠定基礎.
4 數形結合法
數形結合法是一種重要的解題方法,教師在日常的數學教學中可以借助現代化信息技術,培養學生應用數形結合思想解題的思維.例如利用幾何畫板等軟件為學生展示標準圖形,讓學生更加直觀清晰地了解函數圖象的變化過程,加深學生對于函數作圖步驟的印象,從而有效提升學生的解題效率.
5 巧用對稱性
常見的對稱類型函數包括:過原點的一次函數、三次函數(其函數圖形為中心對稱圖形),正弦、余弦函數(其函數圖象為軸對稱圖形)……
例4若函數f(x)=2sin(2x+t-)(0<t<π)是偶函數,求t的值.
解析
方法1定義法
因為f(x)為偶函數,所以對任意實數x,f(-x)=f(x)恒成立.
從而我們可以得到
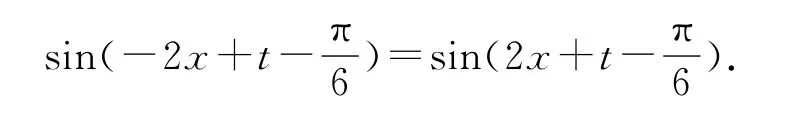
方法2巧用對稱性
因為f(x)為偶函數,所以函數y=f(x)的圖象關于x=0對稱.所以,當x=0時,函數f(x)取得最
點評根據題目所給信息,將偶函數問題轉化成對稱問題,再利用三角函數特殊的對稱性來解決問題,進而可以顯著減少解題運算量,幫助學生更好地理解數形結合思想的本質.
6 三角換元法
三角換元法是高中階段數學教師應逐步引導學生形成、領會的一個重要的解題方法.
例5已知函數,求函 數f(x)的定義域及值域.
解析
由算數平方根的性質得6-x≥0并且6x≥0,我們可以很容易地得出f(x)的定義域為[0,6].
易知f(x)≥0,令x=6sin2t,其中t 的取值范圍為代入f(x)表達式得

點評
利用三角函數sin2x+cos2x=1 的性質,采取三角函數的特殊換元形式對根式下的內容進行化簡,進一步降低了數學計算的復雜性,提高了學生數學解題的正確率.
7 結語
作為高考數學的重要題型之一,函數知識是學生高中階段數學知識學習的重點,同樣也是難點,并且貫穿于整個高中數學知識學習中,在高中數學各個知識點之間起著重要的銜接作用.因此,掌握多樣化的函數題解題技巧,利用多種思維方式求解與函數有關的題目,不僅對于發展學生的創新思維能力、實際應用能力等具有極其重要的作用,同樣也對提升學生的數學學科核心素養具有極其重要的價值.

