發展不平衡視角下地方監管沙盒競爭的演化博弈分析
張紅偉,陳小輝,文 佳,吳永超
(1.四川大學經濟學院,四川 成都 610064;2.中國人民銀行海口中心支行,海南 海口 570105;3.四川大學研究生院,四川 成都 610064)
1 引言
在新一輪科技革命和產業變革的背景下,金融科技(FinTech)成為金融與科技深度融合創新的產物[1],與科技金融是概念截然不同的兩個概念[2]。Arner等[3]進一步指出,2008年以來全球FinTech已進入3.0時代。FinTech使金融體系面臨著一種DNA式的變化,FinTech為代表的金融創新是中國金融崛起的新路徑[4]。另一方面,徐忠等[5]在分析FinTech的風險特性后指出,FinTech還存在監管套利與法律風險,在宏觀層面,一旦風險暴露可能在短時間內迅速演變為大規模的系統性金融風險。柴瑞娟[6]研究指出,FinTech使科技安全風險和傳統金融風險疊加。羅福周等[7]也從機構層面、系統層面剖析了金融科技為金融業發展帶來的風險。
實際上,美國、英國和日本等發達國家也同樣面臨FinTech給其金融體系帶來的積極意義和挑戰問題。怎么辦?2015年3月,英國政府率先提出監管沙盒概念,同年11月英國金融行為局發布監管沙盒白皮書,開始實行監管沙盒,力求促進金融科技發展。新加坡、澳大利亞、泰國、韓國、中國香港和臺灣地區紛紛效仿,相繼推出監管沙盒。
在相關國家和地區紛紛實踐監管沙盒的同時,國內外學者圍繞監管沙盒的概念、積極作用、局限性和中國實施監管沙盒的必要性等進行了較為廣泛的研究。
關于監管沙盒的概念。Castri和Plaitakis[8]認為,監管沙盒是一個受控環境,在該環境中金融創新者可在一定期限內測試其方案而不必立即承擔常規監管成本,且其金融產品也無需滿足現行法律要求。Bromberg等[9]認為,監管沙盒是一個“安全”環境,在這“安全”環境中企業可測試FinTech創新產品,監管機構可視具體案例放松監管規則。蔡瑞娟[6]認為,監管沙盒是一種新的監管工具,旨在為具有破壞性和眾多風險的金融創新提供安全的測試環境和監管實驗區。尹海員[10]認為,監管沙盒主要是以實驗的方式,創造一個“安全區域”,適當放松參與實驗的創新產品和服務的約束,激發創新活力。四個概念均強調監管沙盒可放松監管、促進創新的本質特性。
關于監管沙盒的積極作用。Arner等[11]認為,監管機構在“監管沙盒”中的積極態度,有助于促使監管模式發生轉變。監管機構借助“監管沙盒”建立監管新框架,可提振市場信心[12]。Bromberg等[9]指出,一個良好的監管沙盒應該在測試階段以一種良好的方式保護消費者權益,同時達到緩和金融風險和穩定金融市場的作用。Fan[13]認為,監管沙盒能很好地平衡鼓勵金融創新、保護金融消費者和維護金融穩定三者之間的關系。Chang-Hsien和Peng[14]指出,監管沙盒以一種“輕觸”式監管促進金融創新,同時保護金融消費者權益和防范潛在系統性金融風險。Lee[15]認為,監管沙盒作為一種放松監管的工具,可用于鼓勵金融創新據此發展金融中心。申嫦娥和魏榮桓[16]提出我國要采取友好型監管方式尋找FinTech發展與監管之間的平衡點。徐忠等[5]認為,監管沙盒可為企業提供完善產品和服務的可靠依據,防范潛在金融風險。張景智[17]認為,監管沙盒是現行法律框架下的相機決策制度安排,具有甄別、宣示和窗口作用。這些學者對監管沙盒的作用進行了準確界定。Lee[15]的研究結論表明監管沙盒除作為監管工具外,還是一種“招商引資”工具,中國地方政府推出監管沙盒,“招商引資”也是其主要目的之一。
關于監管沙盒的局限性。Zetzsche等[18]認為監管沙盒高度依賴于現行的監管體制,具有一定的局限性。趙杰等[19]認為,其可能產生新的不公平競爭。
關于中國實施沙盒監管的必要性。徐忠等[5]、蔡瑞娟[6]、張紅偉和陳小輝[20]均傾向于,中國有必要借鑒國外經驗,結合中國實際情況,建設中國監管沙盒,對金融科技實施沙盒監管;徐忠等[5]更進一步,將監管沙盒置于包容性監管體系之內。這些研究成果,在一定程度上解決了中國監管沙盒的必要性問題。
黃震和蔣松成[21]指出,中國和英國已于2017年就金融科技監管沙盒達成了合作協議。截止目前,中國北京市房山區、貴州省貴陽市、江西省贛州市等地方也推出了監管沙盒。那么,在中國幅員遼闊且發展不平衡的背景下,若各地方紛紛推出監管沙盒,其最終結局如何呢?本文基于地方政府的有限理性,采用演化博弈模型,討論前述問題。
本文的創新點和貢獻主要體現在以下三個方面:一是基于中國發展不平衡的基本國情,利用演化博弈模型,率先研究中國各地方監管沙盒競爭的最終結局問題。二是基于支付函數,根據演化博弈分析結果,首次進行了增益分析并據此得出相關命題和推論。三是在相關命題和推論基礎上,首次有針對性地提出了對地方監管沙盒進行中央層面管理的相關政策建議。
2 研究假設
為促進本地金融、經濟發展,地方政府可基于監管沙盒的放松管制和促進FinTech創新等功能實行招商引資。但與其他制度安排不同,監管沙盒在放松管制、促進FinTech創新的同時,會衍生金融風險,并且還可能向異地外溢。另一方面,基于發展不平衡的基本國情,經濟發達地區符合FinTech創新相關風險控制標準的企業和個人(簡稱“潛在適格客戶”)較多,同等條件下FinTech從業機構收入較多,地方政府的收入也較多(這里的地方政府收入指除財政收入等直接收入外,還包括FinTech從業機構解決當地就業問題產生的間接收入);反之,經濟欠發達地區,潛在適格客戶相對較少,同等條件下FinTech創新給地方政府帶來的收入較少。由于FinTech創新始終伴隨著風險,一旦風險發生導致風險事件,將可能給地方政府帶來風險損失成本,此外地方政府推行監管沙盒還將產生固定成本。
地方政府推出監管沙盒后,入駐沙盒內的FinTech從業機構數量記為x,x個FinTech從業機構實施的FinTech創新數量記為y,潛在適格客戶數量記為z,FinTech創新的業務量記為w,則地方政府的收入函數f=f(x,y,z,w)。監管沙盒的風險發現能力記為d,監管沙盒內FinTech從業機構的平均風險管理水平記為l,則監管沙盒內的風險數量r=g(y,w,d,l),風險帶來的損失成本v=v(r),監管沙盒產生的固定成本記為F。則地方政府實施監管沙盒的凈收益
NR=f(x,y,z,w)-v(g(y,w,d,l))-F
(1)
為簡化分析,本文作如下假設。
假設1:邊際收入遞減假設。因給地方政府帶來高收入的FinTech從業機構數量相對有限,隨著入駐監管沙盒內的FinTech從業機構數量x增加,地方政府的收入增加,但邊際收入遞減。由于潛在適格客戶及其有效需求有限,地方政府的收入隨著FinTech創新數量y和業務量w的增加而增加,但邊際收入遞減。因高凈值適格客戶有限,故隨著潛在客戶數量的增加,地方政府的收入會增加,但邊際收入遞減。f(x,y,z,w)的完整假設為在[0,∞)上連續,在(0,∞)內可導,并且具有如下性質:
fx(x,y,z,w)>0,fxx(x,y,z,w)<0;
fy(x,y,z,w)>0,fyy(x,y,z,w)<0;
fz(x,y,z,w)>0,fzz(x,y,z,w)<0;
fw(x,y,z,w)>0,fww(x,y,z,w)<0。
k=x,y,z,w
(2)
假設2:邊際風險遞增假設。因風險的外溢性,風險數量r隨著FinTech創新數量y的增加而增加,且增速遞增。因優質客戶(如信用良好的客戶)數量及其需求相對有限,風險數量r隨著業務量w的增加而增加,且增速遞增。因越隱蔽風險越難發現和管理,風險數量r隨著監管沙盒風險發現能力d和監管沙盒內FinTech從業機構平均風險管理水平l的增加而減少,但減速遞減。g(y,w,d,l)的完整假設為在[0,∞)上連續,在(0,∞)內可導,并且具有如下性質:
gy(y,w,d,l)>0,gyy(y,w,d,l)>0;
gw(y,w,d,l)>0,gww(y,w,d,l)>0;
gd(y,w,d,l)<0,gdd(y,w,d,l)<0;
gl(y,w,d,l)<0,gll(y,w,d,l)<0。
k=y,w
(3)
假設3:邊際損失成本遞增假設。由于風險的傳染性,風險帶來的損失成本v隨著風險數量r的增加而增加,且增速遞增。v(r)的完整假設為在[0,∞)上連續,在(0,∞)內可導,并且具有如下性質:
v′(r)>0,v″(r)>0,v(0)=0。
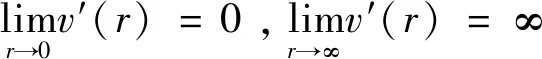
(4)
假設4:凈收益地區差異假設。中國幅員遼闊,但發展不平衡,發達地區和欠發達地區經濟金融發展差距較明顯。FinTech從業機構比較青睞發達地區地方政府的監管沙盒,且入駐發達地區地方政府監管沙盒的FinTech從業機構整體實力較強,發達地區的金融、經濟實力和人才也更具優勢。故,假設發達地區地方政府單獨實施監管沙盒時,其凈收益為正,發達地區地方政府與欠發達地區地方政府同時實施監管沙盒時,發達地區的凈收益可正、可負、也可為零,而欠發達地區地方政府不管單獨實施還是和發達地區地方政府同時實施,其凈收益均可正、可負,也可為零。
3 模型設定
3.1 模型總述
(1)博弈方
根據假設4,中國34個省級、334個地市級和2876個縣級行政單位可劃分為發達地區和欠發達地區,演化博弈在發達地區地方政府群體和欠發達地區地方政府群體之間進行。故,博弈方分別為發達地區地方政府即Developed博弈方,欠發達地區地方政府即Developing博弈方。
(2)博弈方策略
Developed與Developing博弈方均存在“推出監管沙盒,實放松管制和促進FinTech創新”策略和“不推出監管沙盒”策略。故, Developed和Developing博弈方的博弈策略均為(實施、不實施)。
(3)演化博弈穩定點
設Developed和Developing群體中選擇“實施”策略的比例分別為p、q。在qp平面內,按Friedman[22]均衡算法,Developed和Developing博弈方動態博弈的均衡點為E1(0,0)、E2(0,1)、E3(1,0)、E4(1,1)、E5(p**,q**)。當演化博弈結果收斂于穩定點E2(0,1)時,q=0、p=1,即欠發達地區地方政府均選擇“不實施”策略,而發達地區地方政府100%選擇“實施”策略。其他穩定點類推。
(4)博弈方目標
博弈方的目標為最大化其凈收益,博弈雙方的凈收益函數(即博弈方的支付)均為公式(1)、具體變量有別且均受假設1—4約束。具體變量如下:
Developed和Developing博弈方監管沙盒內的FinTech從業機構數量分別記為Ae、Ai。Developed和Developing博弈方監管沙盒內的FinTech創新數量分別記為Ie、Ii。設Developed和Developing博弈方所在地的潛在適格客戶數量分別為Ce、Ci,FinTech創新吸納本地潛在適格客戶的比例為α。
發達地區經濟金融發達,潛在適格客戶較多。因此,設為:
Ce>Ci
(5)
由于FinTech創新具有跨地域服務能力,監管沙盒內的FinTech創新出吸引本地潛在適格客戶外,還會吸引異地潛在適格客戶。設Developed和Developing博弈方監管沙盒內的FinTech創新吸引Developing和Developed博弈方所在地的潛在適格客戶的比例分別為βe、βi,則Developed和Developing博弈方監管沙盒內的FinTech創新吸引的Developing和Developed博弈方所在地的客戶數量分別為βeCi和βiCe。Developed和Developing博弈方監管沙盒內FinTech創新的業務量分別記為We、Wi。
FinTech創新在吸引異地適格客戶的同時,也會向異地外溢風險。設風險外溢因子為γ,則Developed博弈方監管沙盒內FinTech創新產生的風險數量為r時,向Developing博弈方外溢風險的數量為γr。Developing博弈方向Developed博弈方外溢的風險數量也為γr。Developed和Developing博弈方監管沙盒的風險發現能力分別記為de、di。Developed和Developing博弈方監管沙盒內的FinTech從業機構的平均風險管理水平分別記為le、li。設發達地區和欠發達地區監管沙盒的固定成本分別為Fe、Fi。
(5)博弈雙方的支付矩陣
博弈雙方的支付矩陣如表1所示。其中,Developed和Developing博弈方均選擇“實施”策略時,Developed博弈方的支付(payoffs)記為F11,Developing博弈方的支付記為R11。其它情形類推。

表1 Developed博弈方與Developing博弈方的支付矩陣
博弈雙方的支付因雙方策略選擇不同而異,具體如下。
3.2 支付函數
(1)F11和R11
Developed和Developing博弈方均選擇“實施”策略時,Developed博弈方監管沙盒內的FinTech創新的適格客戶總數為αCe+βeCi,Developing博弈方監管沙盒內的FinTech創新吸引的適格客戶總數為αCi+βiCe。
Developed和Developing博弈方監管沙盒內FinTech創新產生的風險數量分別為g(Ie,We,de,le)、g(Ii,Wi,di,li)。
則Developed博弈方承受的風險總數量為:
g(Ie,We,de,le)+γg(Ii,Wi,di,li)
(6)
Developing博弈方承受的風險總數量為:
γg(Ie,We,de,le)+g(Ii,Wi,di,li)
(7)
因此,
F11=f(Ae,Ie,αCe+βeCi,We)-v(g(Ie,We,de,le)+γg(Ii,Wi,di,li))-Fe
(8)
R11=f(Ai,Ii,αCi+βiCe,Wi)-v(γg(Ie,We,de,le)+g(Ii,Wi,di,li))-Fi
(9)
(2)F12和R12
Developed博弈方選擇“實施”策略,Developing博弈方選擇“不實施”策略時,Developed博弈方監管沙盒內的FinTech創新的適格客戶總數為αCe+βeCi,其承受的風險總數量為g(Ie,We,de,le)。Developing博弈方承受的風險總數量為γg(Ie,We,de,le)。因此,
F12=f(Ae,Ie,αCe+βeCi,We)-v(g(Ie,We,de,le))-Fe
(10)
R12=-v(γg(Ie,We,de,le))
(11)
由假設4知:
F12>0
(12)
(3)F21和R21
Developed博弈方選擇“不實施”策略,Developing博弈方選擇“實施”策略時,Developing博弈方監管沙盒內的FinTech創新的適格客戶總數為αCi+βiCe,其承受的風險總數量為g(Ii,Wi,di,li)。Developed博弈方承受的風險總數量為γg(Ii,Wi,di,li)。因此,
F21=-v(γg(Ii,Wi,di,li))
(13)
R21=f(Ai,Ii,αCi+βiCe,Wi)-v(g(Ii,Wi,di,li))-Fi
(14)
4 演化分析
4.1 復制動態方程與雅克比矩陣
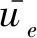
uec=qF11+(1-q)F12
(15)
ueu=qF21
(16)
(17)
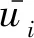
uic=pR11+(1-p)R21
(18)
uiu=pR12
(19)
(20)
則Developed群體選擇“實施”策略的比例的復制動態方程為:
(21)
Developing群體選擇“實施”策略的比例的復制動態方程為:
(22)
為簡化討論,令A=F11-F21,B=F12,D=R11-R12,E=R21。
由(8)式和(13)式,得:
A=f(Ae,Ie,αCe+βeCi,We)-v(g(Ie,We,de,le)+γg(Ii,Wi,di,li))-Fe+v(γg(Ii,Wi,di,li))
(23)
由(9)式和(11)式,得:
D=f(Ai,Ii,αCi+βiCe,Wi)-v(γg(Ie,We,de,le)+g(Ii,Wi,di,li))-Fi+v(γg(Ie,We,de,le))
(24)
由(21)式和(22)式可得雅克比矩陣:
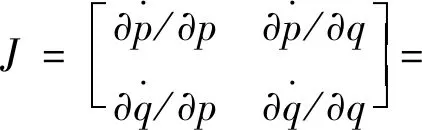
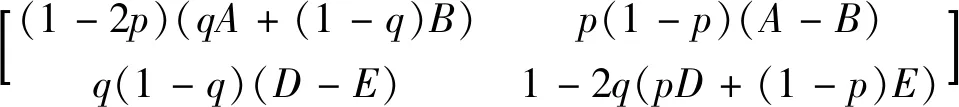
(25)
4.2 復制動態相位圖
4.2.1 Developed博弈方
由(12)式知,B=F12>0。由(10)式和(23)式,得:
B-A=v(g(Ie,We,de,le)+γg(Ii,Wi,di,li))-v(γg(Ii,Wi,di,li))-v(g(Ie,We,de,le))
(26)
構造輔助函數可證明(證明過程可索取):
B-A≥0
(27)
盡管q**取值不在[0,1]上時無意義,但為進行動態關系分析,仍需進行討論:當B=A時,q**=∞;當A=0時,q**=1;當A>0時,q**>1;當A<0時,0 (1)q**=∞ 當B=A時,q**=∞。由(21)式知,dp/dt>0,此時p*=1為ESS(圖1a)。 (2)1 當A>0時,1 (3)q**=1 當A=0時,q**=1。由(21)式知,dp/dt>0,此時p*=1為ESS(圖1c)。 圖1 q**≥1時Developed博弈方復制動態相位圖 (4)0 當A<0時,0 圖2 0 4.2.2 Developing博弈方 由(14)式和(24)式,得: E-D=v(γg(Ie,We,de,le)+g(Ii,Wi,di,li))-v(γg(Ie,We,de,le))-v(g(Ii,Wi,di,li)) (28) 同理,可得: E-D≥0 (29) D和E的符號均不確定,但受(29)式約束。存在p**<0,p**=0,0 均衡點為E1(0,0)、E2(0,1)、E3(1,0)、E4(1,1)、E5(p**,q**)。將q**的四種情況合并為q**>1、q**=1和0 4.3.1q**>1 (1)p**<0。因p**、q**均無意義,因此E5(p**,q**)不在qp單位平面內。此時只有E1(0,0)、E2(0,1)、E3(1,0)、E4(1,1)四個均衡點。此時,(A=B∨A>0)∧(E<0∧D≤E),式中“∨”表示邏輯“或”運算,“∧”表示邏輯“與”運算。當(A=B)∧(E<0∧D≤E)時,由(12)和(25)式可得雅克比矩陣的行列式和跡的符號,由此判斷均衡點的穩定性情況如表2。 表2 雅克比矩陣局部均衡分析 結合相位圖,動態關系及穩定性如圖3a。同理,當(A>0)∧(E<0∧D≤E)時,動態關系及穩定性如圖3a。因此,當(A=B∨A>0)∧(E<0∧D≤E)時,E2(0,1)是穩定點。 其余十四種情形類推,動態關系及穩定點分析如下: (2)p**=0。(A=B∨A>0)∧(E=0∧D<0)時,E2(0,1)是穩定點,動態關系及穩定點如圖3a。 (3)0 (4)p**=1。(A=B∨A>0)∧(E>0∧D=0)時,E4(1,1)是穩定點,動態關系及穩定性如圖3c。 (5)p**>1。(A=B∨A>0)∧(E>0∧D>0∧E≥D)時,E4(1,1)是穩定點,動態關系及穩定性如圖3c。 4.3.2q**=1 (1)p**<0。A=0∧E<0∧DSymbolcB@E,E2(0,1)是穩定點,動態關系及穩定點如圖3a。 (2)p**=0。A=0∧E=0∧D<0,E2(0,1)是穩定點,動態關系及穩定點如圖3a。 (3)0 (4)p**=1。A=0∧E>0∧D=0,E4(1,1)是穩定點,動態關系及穩定性如圖3c。 (5)p**>1。A=0∧E>0∧D>0∧E≥D,E4(1,1)是穩定點,動態關系及穩定性如圖3c。 4.3.3 0 (1)p**<0。A<0∧E<0∧D≤E,E2(0,1)是穩定點,動態關系及穩定點如圖3d。 (2)p**=0。A<0∧E=0∧D<0,E2(0,1)是穩定點,動態關系及穩定點如圖3d。 (3)0 (4)p**=1。A<0∧E>0∧D=0,E3(1,0)是穩定點,動態關系及穩定性如圖3f。 (5)p**>1。A<0∧E>0∧D>0∧E≥D,E3(1,0)是穩定點,動態關系及穩定性如圖3f。 圖3 復制動態關系及穩定性 綜上,Developed群體與Developing群體演化博弈的最終結果可分為四種情形:一個穩定點E2(0,1)、一個穩定點E3(1,0)、一個穩定點E4(1,1)、同時存在E2(0,1)和E3(1,0)兩個穩定點,其具體條件如表3。 穩定點E2(0,1)E3(1,0)E4(1,1)E2(0,1)和E3(1,0)具體條件其他A<0∧E>0∧D≥01.(A=B∨A>0)∧(E>0∧D≥0)2.A=0∧E>0∧D≥0A<0∧E>0∧D<0 表3表明,穩定點的具體條件取決于A、D、B、E取值。影響四者取值的因素及方向如下: 5.1.1 Developed共生增益A A=F11-F21,也就是Developing博弈方選擇“實施”策略時,Developed博弈方選擇“實施”策略與選擇“不實施”策略相比,Developed博弈方增加的支付。由于此時兩博弈方均可能選擇“實施”,故將該支付稱為“Developed共生增益”。A的具體表達式見公式(23)。 (23)式中,Developed博弈方所在地的潛在適格客戶數量Ce和Developing博弈方所在地的潛在適格客戶數量Ci、Developed博弈方監管沙盒的固定成本Fe為外生變量,不受Developed博弈方控制。風險外溢因子γ,Developed博弈方也極難控制,本文將其視為不受Developed博弈方控制。Ii、Wi、di、li四個變量受Developing博弈方控制。因此,Developed博弈方可控制或影響的變量為Ae、Ie、α、βe、We、de、le。其中,Developed博弈方監管沙盒內的FinTech從業機構數量Ae,由其在實施監管沙盒時制定的相關準入政策以及后續招商力度控制;Developed博弈方監管沙盒內的FinTech創新數量Ie,Developed博弈方可通過監管沙盒內的制度約束放松程度、監管沙盒內人才吸引政策等予以控制;FinTech創新吸引本地潛在適格客戶的比例α,Developed博弈方具有一定的影響力,在風險可控條件下,允許FinTech從業機構采用更多的宣傳工具提高α,反之,也可降低α。Developed博弈方監管沙盒內的FinTech創新吸引Developing博弈方所在地的潛在適格客戶的比例βe,Developed博弈方可通過控制跨地域經營的FinTech從業機構數量,影響βe。Developed博弈方監管沙盒內FinTech創新的業務量We,出于防范風險等需要,Developed博弈方可能通過規定最高業務量限額等措施施加影響之。Developed博弈方監管沙盒的風險發現能力de,Developed博弈方可通過改進監管沙盒的質量進行控制。Developed博弈方監管沙盒內的FinTech從業機構的平均風險管理水平le,Developed博弈方既可以通過監管沙盒的準入政策予以控制,也可采取后續風險提示、專業人員培訓等方式進行控制。Ae、Ie、α、βe、We、de和le等變量的影響方向,具體如下: (1)Ae、α、βe 公式(23)對Ae求偏導,結合(2)式得:?A/?Ae=fAe>0。因此,監管沙盒內FinTech從業機構數量越多,Developed共生增益越大。同理,(23)式分別對α、βe求偏導,結合(2)式可得:?A/?α>0、?A/?βe>0,即A隨著α、βe的增加而增加。 (2)創新數量Ie 公式(23)對Ie求一、二階偏導,由(2)、(3)、(4)式知,存在唯一ξIe∈(0,∞),在其他條件不變情況下,當Ie∈(0,ξIe)時,A隨著Ie增加而增加;當Ie∈(ξIe,∞)時,A隨著Ie增加而減少。 (3)業務量We 公式(23)對We求一、二階偏導,結合(2)和(3)式知,存在唯一ξWe∈(0,∞),在其他條件不變情況下,當We∈(0,ξWe)時,A隨著We增加而增加,當We∈(ξWe,∞)時,A隨著We增加而減少,當We=ξWe時,A取最大值。 (4)de和le 另一方面,受Developing博弈方控制的Ii、Wi、di、li四個變量,也會對Developed的共生增益產生影響。具體如下: (5)Ii和Wi 公式(23)對Ii求一階偏導,得?A/?Ii=γgIi[v′(γg(Ii,Wi,di,li))-v′(g(Ie,We,de,le)+γg(Ii,Wi,di,li)],由(3)和(4)式知,?A/?Ii<0。同理,對Wi求一階偏導,可得,?A/?Wi<0。即,Developed共生增益A隨著Developing博弈方監管沙盒內的創新數量Ii和監管沙盒內創新的業務量Wi的增加而減少,且與自身沙盒內的創新數量Ie、和業務量We不同,Ii和Wi并不存在臨界點,而是隨著兩者的增加而單調減少。 (6)di和li 公式(23)對di求一階偏導,?A/?di=γgdi[v′(γg(Ii,Wi,di,li))-v′(g(Ie,We,de,le)+γg(Ii,Wi,di,li)],由(3)和(4)式知,?A/?di>0。同理,對li求一階偏導,可得,?A/?li>0。與Ii和Wi相反,Developed共生增益A隨著di和li的增加而單調增加。 綜合對Developed共生增益A的分析,可得如下命題1。 命題1:Developed和Developing博弈方均可改變Developed共生增益A。但雙方控制的變量和影響方向不同。Developed博弈方可控制的變量有Ae、Ie、α、βe、We、de、le,其中A隨Ae、α、βe、de和le的增加單調增加,le和We存在臨界點,臨界點以下A隨Ie和We的增加單調增加,臨界點以上隨Ie和We的增加單調減少,臨界點處取最大值。Developing博弈方可控制的變量有Ie、We、de、le,其中A隨Ii和Wi的增加單調減少,隨di和li的增加單調增加。 5.1.2 Developing共生增益D D=R11-R12,Developed博弈方選擇“實施”策略時,Developing博弈方選擇“實施”策略與選擇“不實施”策略相比,Developing博弈方增加的支付。同理,將該支付稱為“Developing共生增益”。D的具體表達式見公式(24)。 由于(23)式和(24)式具有對稱性,比照命題1,可得命題2。 命題2:Developed和Developing博弈方均可改變Developing共生增益D。但雙方控制的變量和影響方向不同。Developing博弈方可控制的變量有Ai、Ii、α、βi、Wi、di和li,其中D隨Ai、Ii、α、βi、di和li的增加單調增加,Ii和Wi存在臨界點,臨界點以下D隨Ii和Wi的增加單調增加,臨界點以上隨Ii和Wi的增加單調減少,臨界點處取最大值。Developed博弈方可控制的變量有Ie、We、de、le,其中D隨Ie、We的增加單調減少,隨de和le的增加單調增加。 由命題1和命題2,可得如下推論1、2、3。 推論1:Developed和Developing雙方之間的博弈,競爭FinTech從業機構并非唯一路徑,改進自身監管沙盒質量、提高監管沙盒風險發現能力,提供風險提示等服務、改善FinTech從業機構平均風險管理水平等也是可能路徑,而且是更可控制的精細化路徑。 推論2:監管沙盒風險發現能力和監管沙盒內FinTech從業機構平均風險管理水平的提高,具有正外部性;監管沙盒內FinTech創新數量和創新業務量具有負外部性。 推論3:在承擔風險損失成本(即對監管沙盒內的風險承擔責任)的情況下,出于提高共生增益A、D考慮,地方政府將會理性控制其建立的監管沙盒內的FinTech創新數量和創新的業務量,不會讓其無限度增加。但若不承擔風險損失成本,則其出于提高共生增益A、D考慮,將可能無限度增加其建立的監管沙盒內的FinTech創新數量和創新的業務量。 5.2.1 Developed獨建增益B B=F12,即Developing博弈方選擇“不實施”策略時,與選擇“不實施”策略獲得的支付相比,Developed博弈方增加的支付。由于此時僅Developed博弈方選擇“實施”,故將該支付稱為“Developed獨建增益”。B的具體表達式見公式(10)。公式(10)中,Ae、Ie、α、βe、We、de和le為Developed博弈方可控制的變量,Ce、Ci和Fe為外生變量,但與共生增益A不同的是,Developing博弈方并不能影響B。對(10)式求偏導,可得命題3。 命題3:僅Developed博弈方可改變Developed獨建增益B。Developed博弈方可控制的變量有Ae、Ie、α、βe、We、de和le,其中B隨Ae、α、βe、de和le的增加單調增加,Ie和We存在臨界點,臨界點以下B隨兩者的增加單調增加,臨界點以上隨兩者的增加單調減少,臨界點處取最大值。 5.2.2 Developing獨建增益E E=R21,即Developed博弈方選擇“不實施”策略時,與選擇“不實施”策略獲得的支付相比,Developing博弈方增加的支付。同理,稱為“Developing獨建增益”。E的具體表達式見公式(14)。由于(14)式和(10)式具有對稱性,比照命題3,可得如下命題4。 命題4:僅Developing博弈方可改變Developing獨建增益E。Developing博弈方可控制的變量有Ai、Ii、α、βi、Wi、di和li,其中E隨Ai、α、βi、di和li的增加單調增加,Ii和Wi存在臨界點,臨界點以下E隨兩者的增加單調增加,臨界點以上隨兩者的增加單調減少,臨界點處取最大值。 由命題3和命題4,可得推論4。 推論4:在承擔風險損失成本(即對監管沙盒內的風險承擔責任)的情況下,出于提高獨建增益B、E考慮,地方政府將會理性控制其建立的監管沙盒內的FinTech創新數量和創新的業務量,不會讓其無限度增加。但若不承擔風險損失成本,則其出于提高獨建增益B、E考慮,將可能無限度增加其建立的監管沙盒內的FinTech創新數量和創新的業務量。 根據表3,結合增益分析,可得如下結論: (一)地方監管沙盒具有較好的可行性。從表3可知,發達地區和欠發達地區地方政府群體演化博弈的最終結果并不收斂于E1(0,0)。因此,地方監管沙盒具有較好的可行性。 (二)欠發達地區監管沙盒仍有一定生存空間。從表3可知,在本文討論的十五種情形中,有兩種情形僅欠發達地區地方政府群體100%選擇“實施”監管沙盒,而發達地區100%選擇“不實施”;四種情形下,發達地區和欠發達地區地方政府群體均 100%選擇“實施”監管沙盒;一種情形下,欠發達地區地方政府可能100%選擇“實施”監管沙盒,而發達地區100%選擇“不實施”,取決于初始情況。總之,欠發達地區地方監管沙盒仍有一定生存空間。 (三)地方監管沙盒的最終結局具有較高的依存性。在發達地區和欠發達地區均選擇“實施”監管沙盒的情況下,兩類群體演化博弈的最終結局未必是均100%選擇“實施”監管沙盒。依據四個命題及相應推論,最終結局取決于各自的獨建增益和共生增益,但獨建增益和共生增益除受自身控制外,共生增益還受對方正外部性和負外部性的影響。因此,不管是發達地區還是欠發達地區地方政府,任何一方均無法單方面決定自身監管沙盒的最終結局,兩者之間存在較高的依存性。 依據推論1、3、4,建議如下: (一)建議中央層面對地方監管沙盒的質量(尤其是風險發現能力)及監管沙盒內FinTech從業機構的平均風險管理水平進行適度評價,一來緩解地方監管沙盒之間對FinTech從業機構的競爭,二來增加地方監管沙盒的正外部性以對沖FinTech創新給其他地方帶來的負外部性。 (二)地方監管沙盒對鼓勵FinTech創新、防控金融風險具有重要意義。為避免地方政府逆向選擇,建議中央層面明確監管沙盒內FinTech創新產生的風險損失成本應由建設監管沙盒的地方政府承擔,以促使其自覺將創新數量和業務量控制在可控范圍之內。 綜合全文看,本文利用演化博弈模型對發達和欠發達兩類地區之間的監管沙盒競爭問題進行了研究,得出了兩類地區監管沙盒之間存在較高依存關系等結論,并給出了相關建議。但中國金融監管機構若推出監管沙盒,其與地方監管沙盒之間將是怎樣的關系?兩類監管沙盒之間將如何協調聯動?在“有風險沒有及時發現就是失職”之新問責機制下,各類監管沙盒將如何演進?這些問題均有待進一步研究。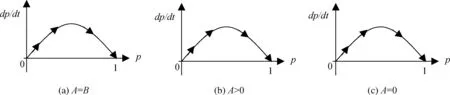
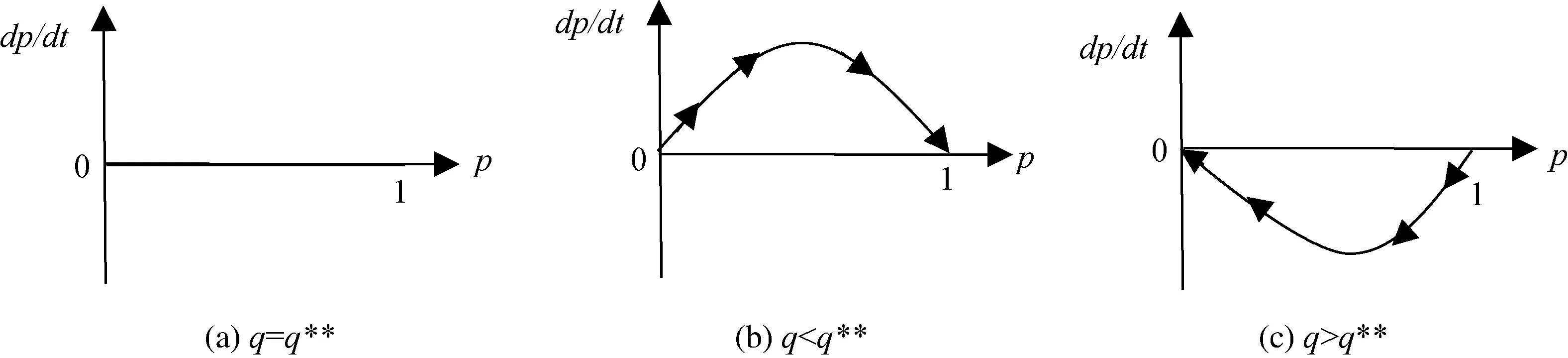
4.3 復制動態的關系及穩定性分析

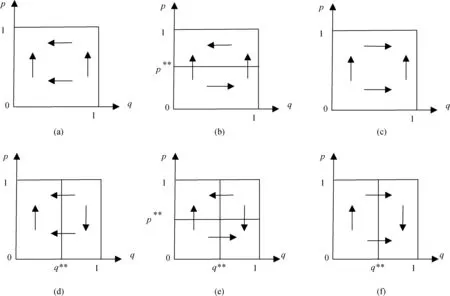
5 增益分析
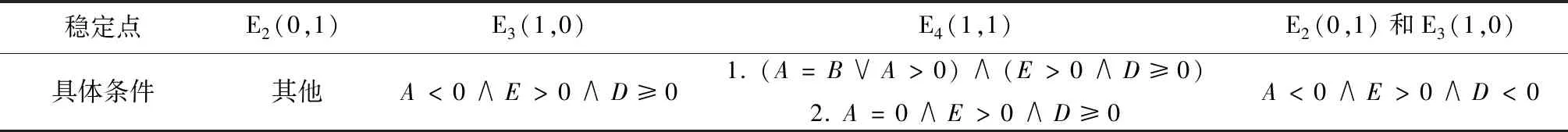
5.1 共生增益A、D、分析
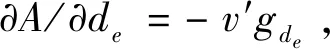
5.2 獨建增益B、E分析
6 結語

