班輪企業合并背景下的服務網絡優化

趙曉燕， 胡堅堃， 黃有方

(上海海事大學 物流研究中心, 上海 201306)

近年來，隨著世界各國國內生產總值(Gross Domestic Product,GDP)增速減慢、貿易總量增長乏力，航運市場整體需求不振，集裝箱運輸市場供需嚴重失衡，多數班輪企業出現業績虧損、入不敷出的情況，運營壓力持續增大。2016年起，我國的大型航運公司開始進行兼并重組，與以往班輪聯盟采取共同派船、艙位租用等手段聯合調度不同，班輪企業合并之后仍面臨著服務網絡深層次調整的需求等諸多問題。本文主要研究班輪企業合并后如何對服務網絡進行優化調度，實現資源的進一步整合。

目前，國內外對服務網絡優化的研究已取得不少成果，例如:MENG等[1]研究班輪服務網絡設計問題,并具體介紹“航段”的概念；壽涌毅等[2]在船舶調度問題中引入港口時段和班次要求；張芳軍等[3]通過箱種代用的方式優化班輪公司航線，減少空箱調運量；MONEMI等[4]研究班輪網絡設計、船隊部署和空箱調運的問題，將服務網絡的數量和設計作為內生變量進行求解；AKYUZ等[5]考慮船速和運輸時間限制因素，研究服務網絡分配和集裝箱路徑問題；楊秋平等[6]在規劃期內以獲得最大的折現值為目標，提高班輪公司的營運現金流量，進行船隊規劃；張芳軍[7]采用多類型集裝箱箱種代用和投入使用可折疊空箱兩種方式優化空箱調運,并進行對比分析；于冬艷[8]基于降低運輸成本的目標，考慮碳排放造成的環境成本。此外，關于班輪公司聯盟或合并問題的研究也有很多，例如：PANAYIDES等[9]對班輪航運全球聯盟的穩定性進行評估；ALIX等[10]強調聯盟并不是在全球航運業中生存的唯一途徑，為后來班輪企業合并提供借鑒；吳瓊等[11]以獲得聯盟整體利潤最大為目標，研究班輪聯盟網絡優化問題；陳繼紅等[12]在航運聯盟下，采用改進的班輪配船模型研究箱位租賃問題，并進行航線規劃;楊華龍等[13]基于集裝箱運輸需求的隨機波動性，研究近洋航線艙位互租與艙位分配綜合規劃問題。

以往的研究也存在一些不足：

1) 對集裝箱調度優化問題的研究大多以單個承運人航線運營收益最大或成本最小為目標，對班輪公司合并后資源整合的研究較少；

2) 以往的航運聯盟是基于艙位租用和共同派船等方式實現戰略聯合調度的，很少涉及服務網絡變化和航線結構調整。

本文從服務網絡整合的角度出發，考慮船型配置、船速設定和空重箱運輸之間的關聯性，建立班輪公司合并后服務網絡調度優化模型，并以原中國遠洋運輸集團(以下簡稱中遠)與原中國海運集團(以下簡稱中海)合并為例進行模型驗證，對班輪公司合并前后的航線網絡和運輸成本進行對比。

1 問題描述

將班輪航線的掛靠港口作為節點，由節點和有向邊組成班輪服務網絡，建立基于多港掛靠和軸輻式網絡的班輪服務網絡優化模型。該模型在混合運輸網絡下運行，即各港口之間既有直線運輸又有中轉運輸。甲和乙在亞洲—大洋洲區域的班輪網絡分別見圖1和圖2。

航線1：上海—新加坡—布里斯班—悉尼—墨爾本—橫濱—上海(如圖1所示)。航線2：新加坡—墨爾本—悉尼—布里斯班—新加坡(如圖1所示)。航線3：上海—香港—悉尼—墨爾本—布里斯班—高雄—香港—上海(如圖2所示)。航線4：巴生—新加坡—悉尼—墨爾本—阿德萊德—巴生(如圖2所示)。

2個班輪網絡均覆蓋上海港、新加坡港、布里斯班港、悉尼港和墨爾本港。首先確定甲、乙兩公司的船型運力和運營成本，然后隨機生成運輸需求，將5個重合港口的運輸需求合并。結合航段集、航程集、港口空箱數據和重箱運輸計劃，并將船型、航速、重箱量、空箱量和航行時間等作為決策變量，將航行成本和在港成本構成的總運輸成本最小作為目標函數，確定航線配船類型、數量、船速、空重箱調運方案和裝卸時間等。

2 班輪服務網絡優化調度模型

2.1 模型假設

1) 班輪航線、掛港順序和船型種類已給定。

2) 假設每條航線的規劃期相同。

3) 假設所有集裝箱都是國際標準箱，不考慮集裝箱的大小差異。

4) 假設空箱可在任何港口中轉。

5) 假設同一船型船舶在不同港口的裝卸費和裝卸效率相同。

2.2 參數和決策變量

2.2.1航線和船舶參數

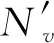
2.2.2時間參數

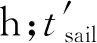
2.2.3成本參數

Cv為v類型船舶每周的航行費用，包括船員工資、船舶折舊費、保險費、維護維修費和管理費用等；Qvs為v類型船舶在sv的速度下的油耗量，t/h；η為油價，美元/t；fh為重箱的單位裝卸成本，美元/箱次；fe為空箱的單位裝卸成本，美元/箱次；ft為船舶在港口的停靠成本，美元/h；e為港口的裝卸效率，h/TEU。

2.2.4決策變量

αlvs為0或1變量，當航線l上分配的v類船舶以速度s航行時，αlvs=1，否則αlvs=0；αvl為0或1變量，當航線l上分配v類型船舶時,αvl=1，否則αvl=0；Qdl為從港口m到港口n這段航程d上運輸的重箱量；Qkl為通過航線l運輸的重箱運輸方案k上的重箱運輸量；Qpyl為在航線l上港口p裝運的空箱作業量；Qpxl為在航線l上港口p卸載的空箱作業量；Qel為在航線l上兩個相鄰港口組成的航段k運輸的空箱量。

2.3 成本分析

總運輸成本主要分為航行成本和在港成本，其中:航行成本是指在船舶航行時產生的成本，與航行時間有關；在港成本是指船舶到港后產生的成本，主要與船舶噸位和裝卸箱量有關，包括進港費用、裝卸成本和在港等待的時間成本等。

2.3.1航行成本

航行成本分為船舶的油耗費用和船舶的固定運營成本2種，主要包括船員工資、船舶折舊費、保險費、維護維修費和管理費用等。由于不同航線的里程不同,不同船舶的單位油耗也不同。在一周的時間內,所有航線的航行總成本為

(1)

2.3.2在港成本

船舶在港成本分為2種:一種是重箱和空箱的裝卸費，與裝卸的集裝箱量和單個集裝箱的裝卸費用有關；另一種是船舶在港等待發生的時間成本。裝卸成本和時間成本合計為在港成本，即

(2)

2.4 模型建立

minW=W1+W2

(3)

(11)

(12)

(13)

αlvs∈{0,1},l∈L;v∈V;s∈Sv

(14)

αvl∈{0,1},l∈L;v∈V

(15)

Qd,l≥0,Qkl≥0,Qpyl≥0,Qpxl≥0,Qel≥0

(16)

Nvl∈{0}∪Z+

(17)

式(3)由船舶油耗成本、周固定運營成本、重箱空箱裝卸成本和在港等待時間成本等4部分構成，使總運輸成本最小;式(4)為當運行完單個航次的時間為tsail時，在規劃期t內，為確保掛靠頻率為fl，班輪公司在航線l上要投入運營的船舶總數量約束；式(5)為班輪公司投入到航線l上v類型船舶的數量不超過其擁有的v類型船舶的數量；式(6)為合并后的班輪公司在航線l上要投入運營的船舶總數量約束；式(7)為合并后的班輪公司投入到航線l上v類型船舶的數量不超過其擁有的v類型船舶的數量；式(8)為容量限制，在航線的任何航段或航程中，重箱和空箱的數量不超過該航線上船舶的運載能力；式(9)假定每條航線只配置1種船舶或取消運營；式(10)為需求守恒約束，要求每個OD需求被滿足；式(11)為空箱調運平衡約束，即航線上所有的空箱需求量被滿足；式(12)為保證從第1個港口到第n個港口的空箱需求得到滿足；式(13)為保證航行時間、重箱裝卸時間、空箱裝卸時間之和不超過航行規劃期的最大時間；式(14)為航線l上分配的v類型船舶以速度s航行時，αlvs=1，否則αlvs=0；式(15)為航線l上分配v類型船舶時，αvl=1，否則αvl=0；式(16)為對某些決策變量的非負約束；式(17)為某決策變量的正整數約束。

3 算例與分析

3.1 算例描述

以原中國遠洋集裝箱運輸集團有限公司(A)、原中國海運集裝箱運輸有限公司(B)兩家班輪公司在亞洲—大洋洲—歐洲區域具有代表性的部分航線為實例，對上述模型進行驗證。其中:A公司的班輪網絡包括22個港口12條候選航線(見表1)；B公司的班輪網絡包括43個港口11條候選航線(見表2)；2家公司和合并后的公司船隊中各有4種類型的船舶，分別對各公司各類型船舶每周的航行費用進行統計(見表3～表5)。不同類型的船舶在不同航速下消耗的燃油有所不同(見表6)。

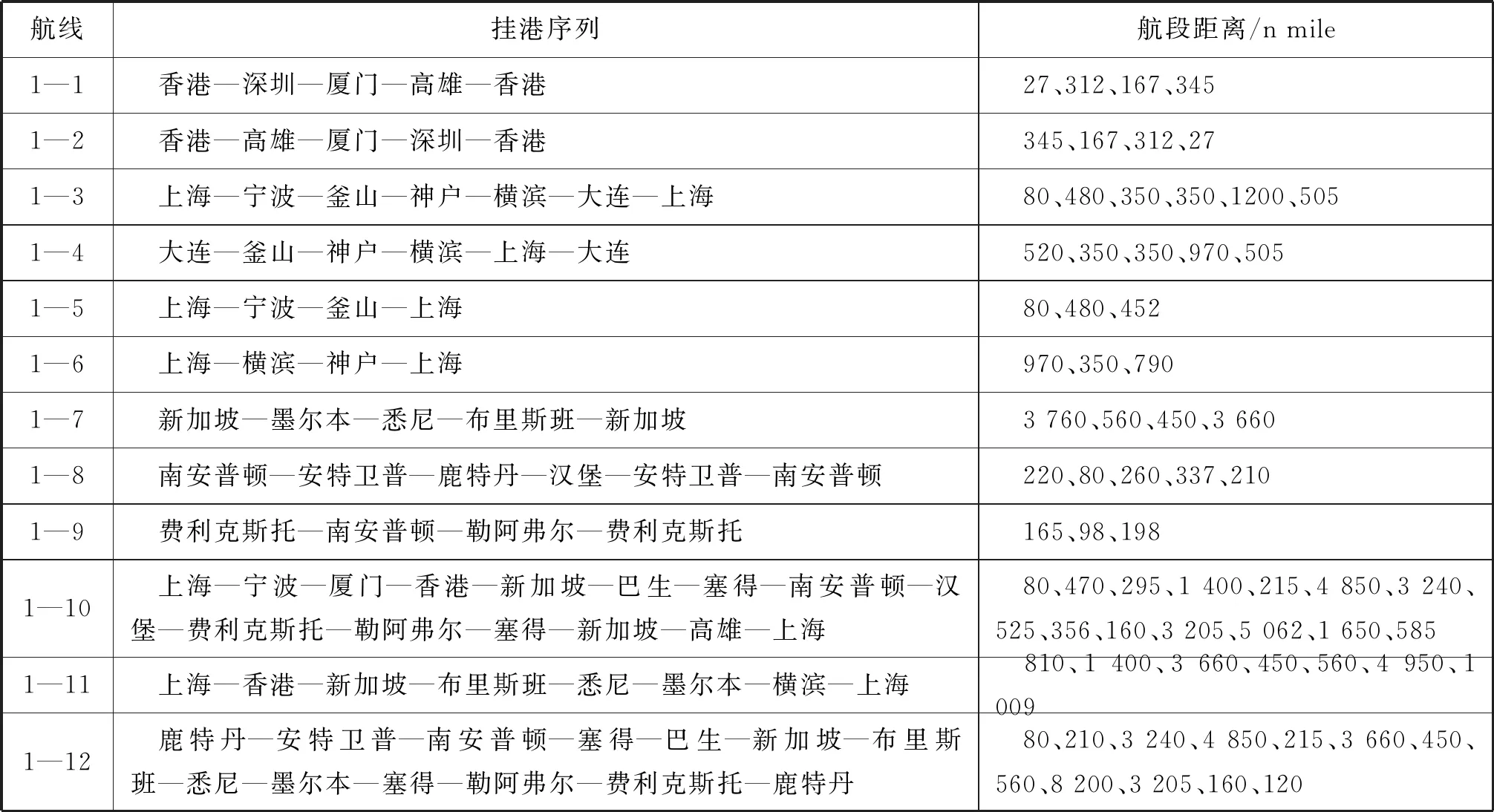
表1 A公司部分航線

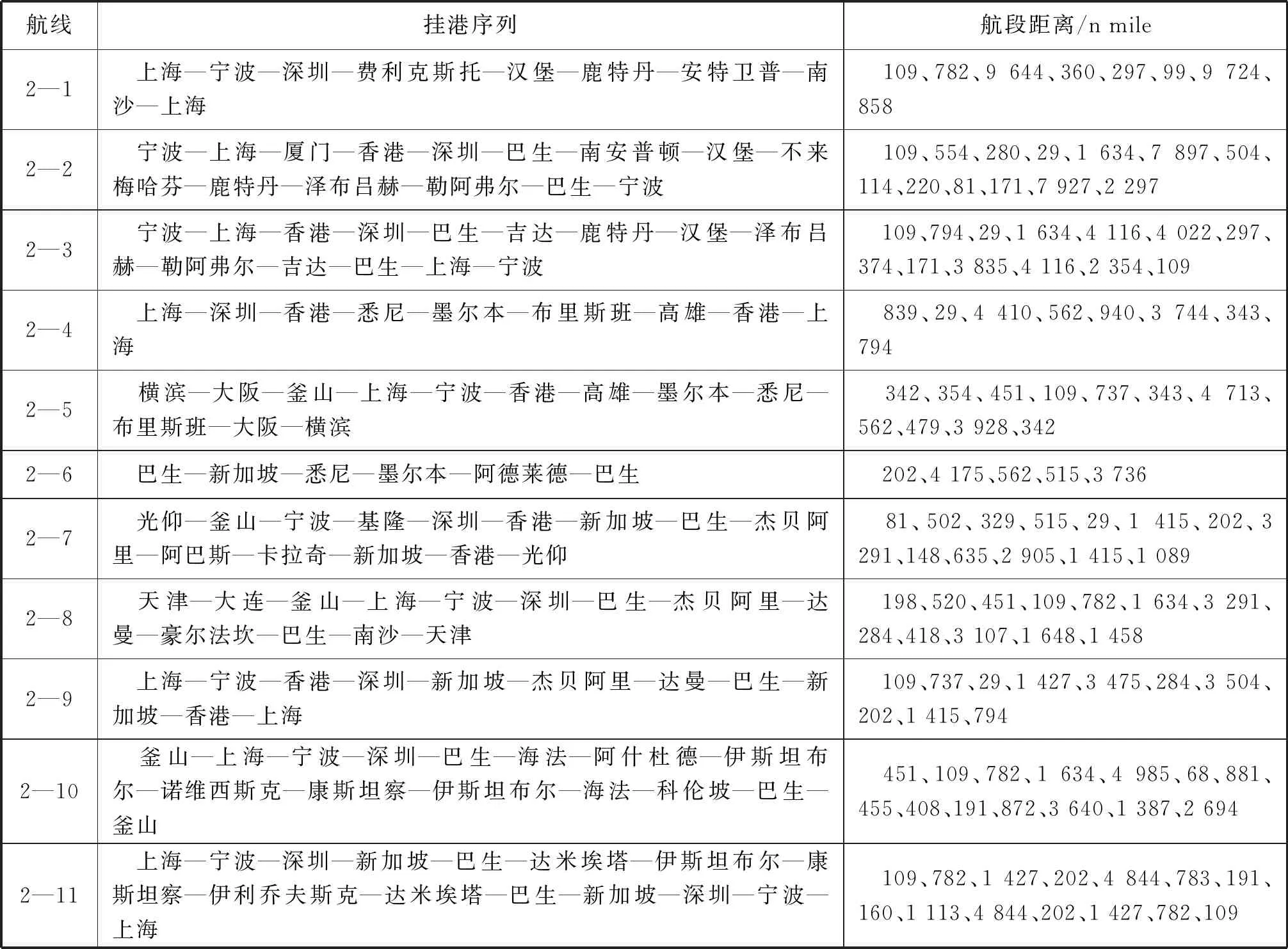
表2 B公司部分航線

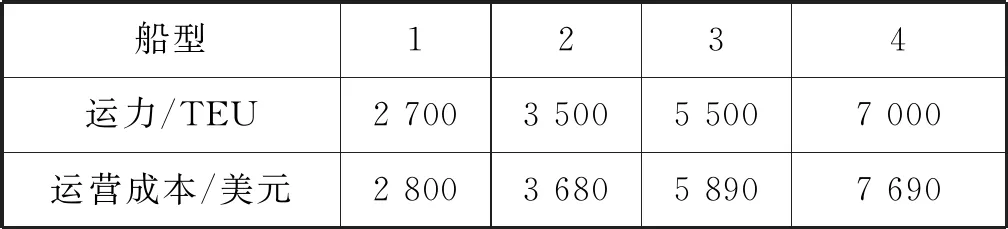
表3 A公司主要船型的運力和運營成本

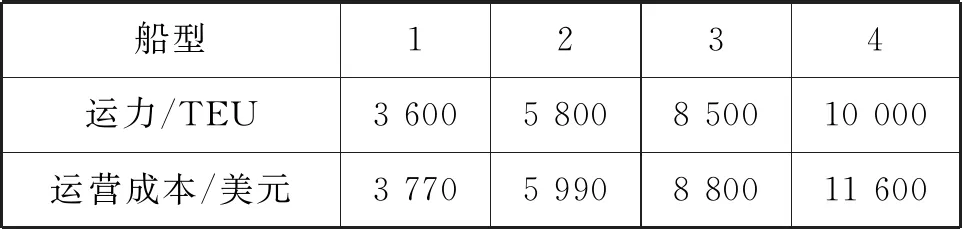
表4 B公司主要船型的運力和運營成本

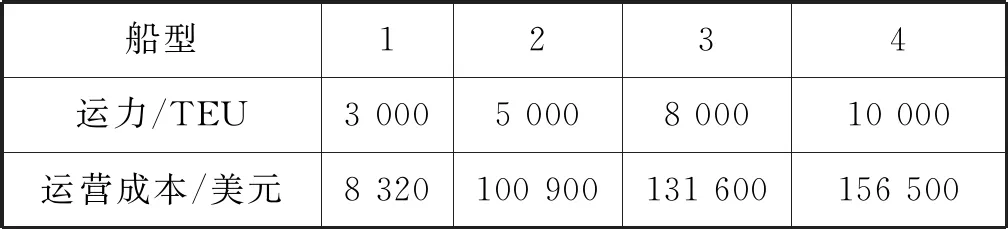
表5 A公司和B公司合并后的船型運力和運營成本

3.2 優化結果和分析

隨機生成OD(Origin-Destination)運轉需求，符合[50，200]的均勻分布。令油價η為620美元/t，空箱裝卸費為50美元/TEU，重箱裝卸費為70美元/TEU。在VS2010環境下調用Gurobi求解器對模型進行求解。在對航線進行篩選和更新后，得到優化結果見表7，其中數據表示A公司和B公司合并后14條航線的船型配置、航速和航行時間情況。由于運輸需求的合并，航線1—1、1—4、1—5、1—6、1—7、1—9、1—11、2—3和2—6均未被選擇。通過算例可知：當A公司和B公司獨自承擔運輸時，在航行周期內最小運輸成本分別為28 878 846美元和43 318 270美元，合計為72 197 116美元；而在A公司與B公司合并之后，運輸成本為63 569 120美元，較合并之前降低13.57%。

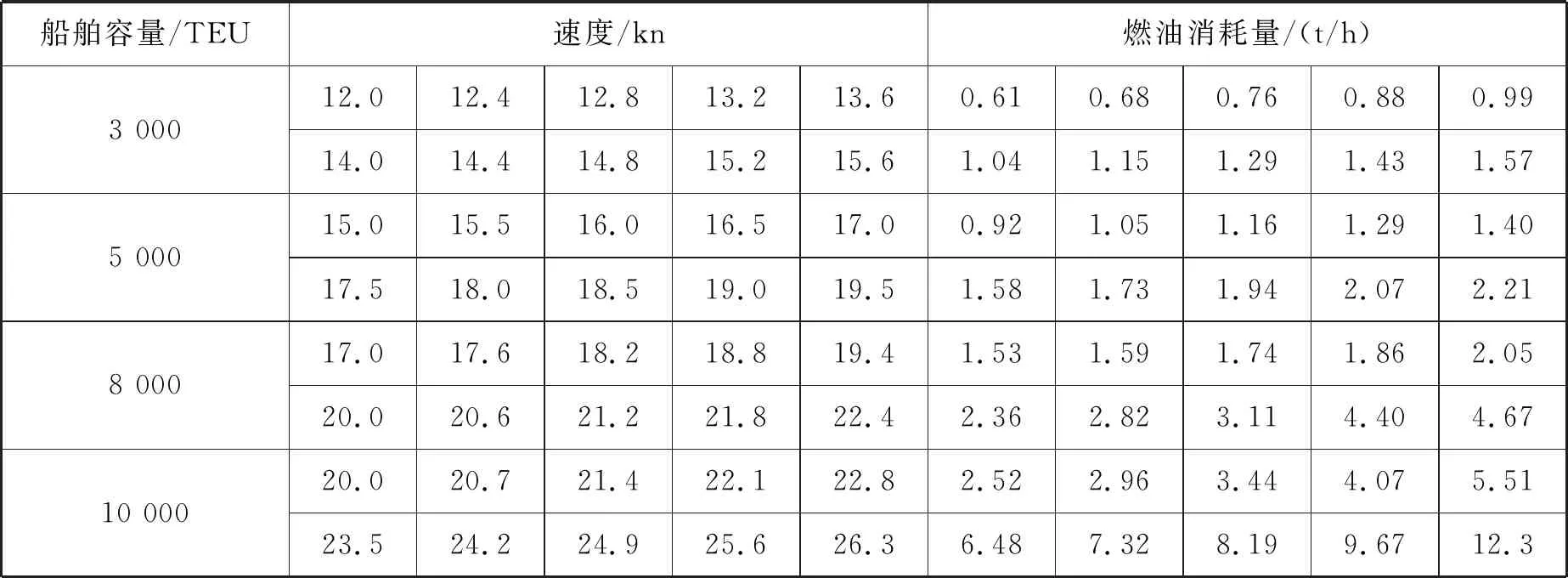
表6 船舶燃油消耗和運行成本

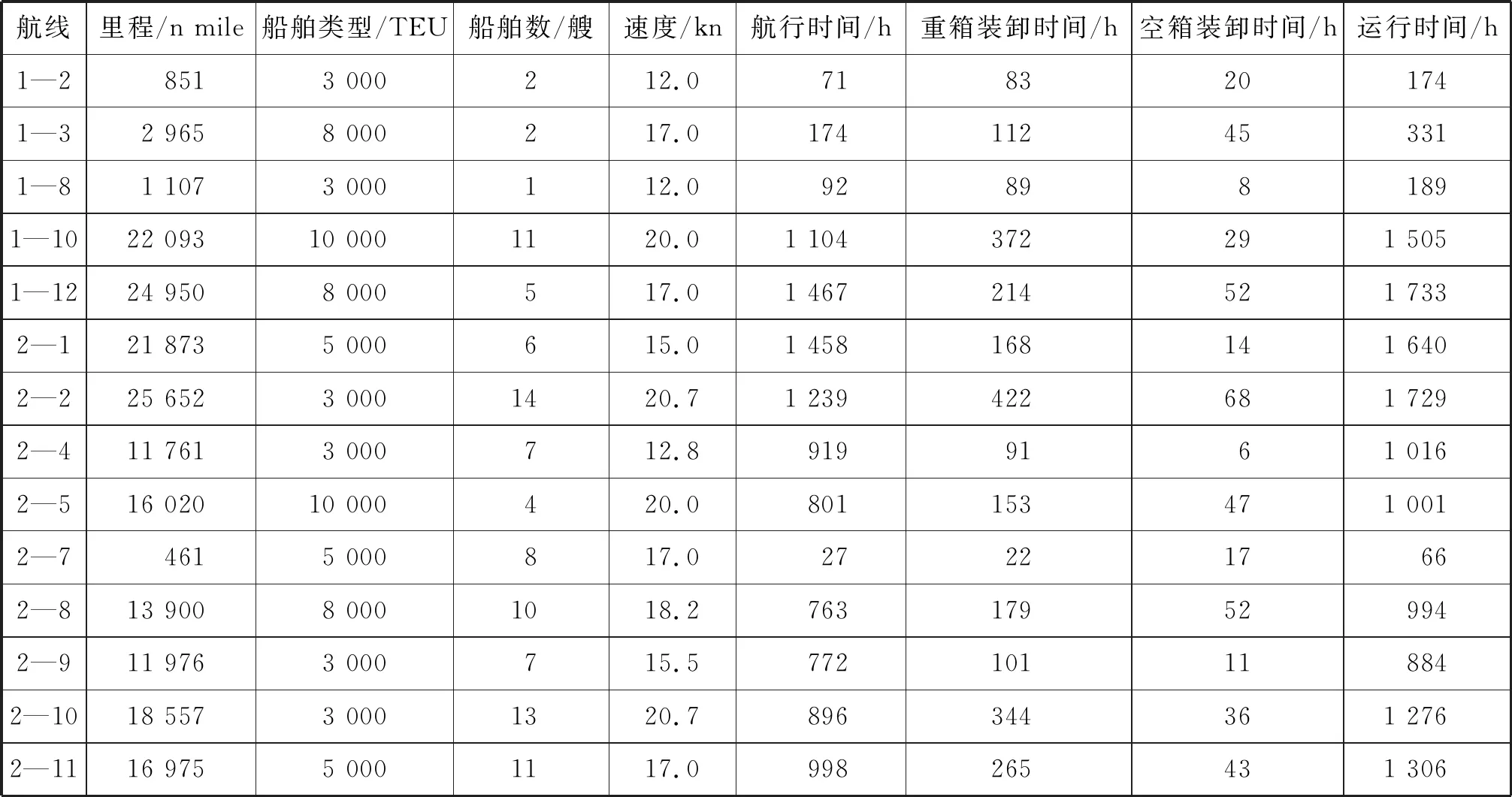
表7 優化結果

3.3 靈敏度分析

為考查重箱裝卸費對班輪公司合并后路徑選擇和運輸成本的影響(見圖3)，在空箱裝卸費和油價不變的情況下，分析重箱裝卸費為50美元、70美元和100美元時服務網絡調度的變化。結果顯示：當重箱裝卸費變化時，2家公司合并后的路徑選擇沒有發生變化，仍為14條航線，這是由于重箱裝卸費的變化在所有航段同時發生。此外，重箱裝卸費的增加使得班輪公司合并后的港口成本大幅提高，迫使船舶提升裝卸效率、縮短裝卸時間和航行周期，從而將增加的港口裝卸成本轉移到航行成本中。

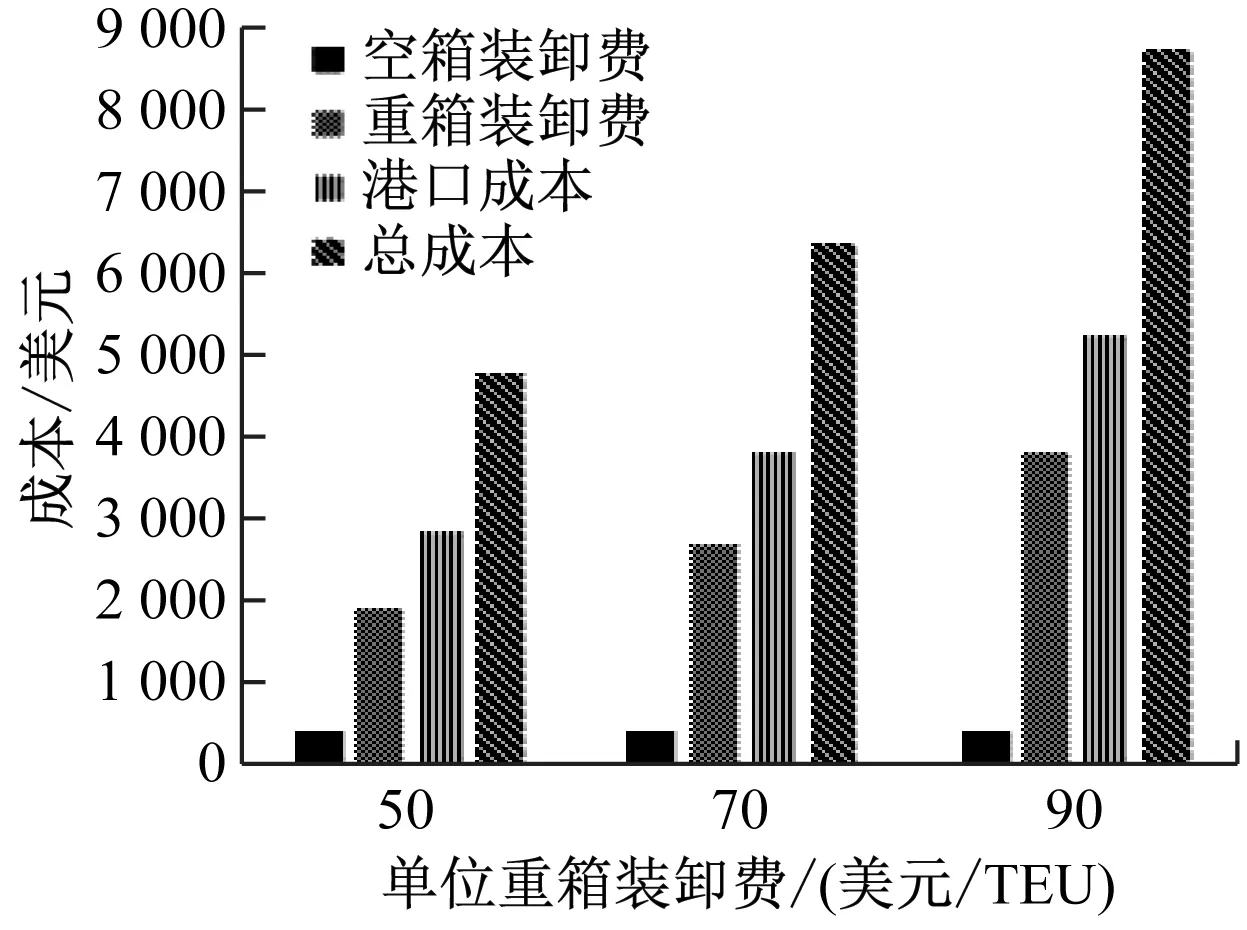
圖3 班輪公司合并后重箱裝卸費對運輸成本的影響

4 結束語

本文討論企業合并的背景下班輪公司服務網絡調度優化問題，考慮船舶油耗成本、周固定運營成本、重箱空箱裝卸費和在港等待時間成本，建立基于混合運輸網絡的服務網絡優化模型。同時，采用A公司和B公司合并的航線和運行數據進行實證分析。優化結果表明：通過公司合并實現對服務網絡的優化調度，可節省運輸成本8 627 996美元，比合并前下降約13.57%；靈敏度分析結果表明：重箱裝卸費的增加迫使船舶提升裝卸效率，將增加的港口裝卸成本轉移到節約的航行成本中。

本文對集裝箱網絡運輸問題的研究還存在一些不足之處，后續可在以下2方面拓展研究：

1) 模型未涉及同一航線配置多種船型的情形，可在模型中加入該情形進行研究。

2) 著重研究班輪公司合并后服務網絡的初步變化，并未深入分析航線網絡結構的調整問題，需在以后的研究中進一步拓展。