噴漿臺車機械臂的靜動態特性分析及拓撲優化

李若昕，姜永正, ，陸小龍，夏啟航

（1.湖南科技大學 機電工程學院，湖南 湘潭 411201；2.湖南科技大學 機械設備健康維護湖南省重點實驗室，湖南 湘潭 411201）

0 引言

噴漿臺車是當前隧道、涵洞等地下建筑進行噴漿支護時的主要工具，隨著現代工程建設的大規模開展，對噴漿臺車的需求量大大增加[1]。現代的噴漿機械臂朝著大型化和智能化方向發展，機械臂的響應快速性和穩定性是一個很重要的設計要求[2]。又因為地下建筑的施工環境較為惡劣，機械臂的俯仰運作頻繁，機械臂受力情況復雜，導致機械臂在運作過程中易開裂，對施工人員的生命安全造成威脅[3]。為保證施工人員的生命財產安全，提高施工效率，延長噴漿臺車機械臂的使用年限，對噴漿臺車機械臂的分析研究顯得十分必要。

據調查了解，在大部分工廠中，他們對于機械臂開裂問題的解決方法多是對開裂處進行加厚處理，這解決了一時的開裂問題，但是未從機械臂強度等方面對機械臂本身的缺陷進行分析，加厚的機械臂后期仍然會出現問題，故這種解決方法治標不治本[4]。在航天、航空、汽車等高科技工業領域中，面對臂管開裂的情況，設計者廣泛應用拓撲優化這一優化方法加以解決。如S.Mantovani 等[5]對汽車的儀表板進行了拓撲優化，最終設計出了一款高性能跑車儀表板；M.Imran 等[6]對飛機起落架進行有限元分析，并對飛機起落架結構進行了合理的改進。

綜上所述，拓撲優化能夠在材料均勻分布的設計空間中找出最佳的分布方案[7]，并且能夠為實物的優化改進設計提供良好的理論基礎。但是在傳統的工業領域中，拓撲優化的運用卻略顯匱乏。因此本文以噴漿臺車機械臂作為研究對象，且為了研究靜態情況下以柔度為目標函數的機械臂拓撲結構，建立了機械臂的有限元模型，利用美國Altair公司HyperMesh系列軟件中Optistruct 對機械臂單獨進行有限元分析，并通過對比有限元仿真模擬實驗[8]結果，對機械臂進行了簡單的拓撲優化分析。并通過拓撲優化所得結果對機械臂進行了改良，分析結果對比證實該優化取得了良好的效果。

1 現有機械臂建模及特性分析

1.1 機械臂有限元模型

噴漿臺車大臂的結構組成見圖1。

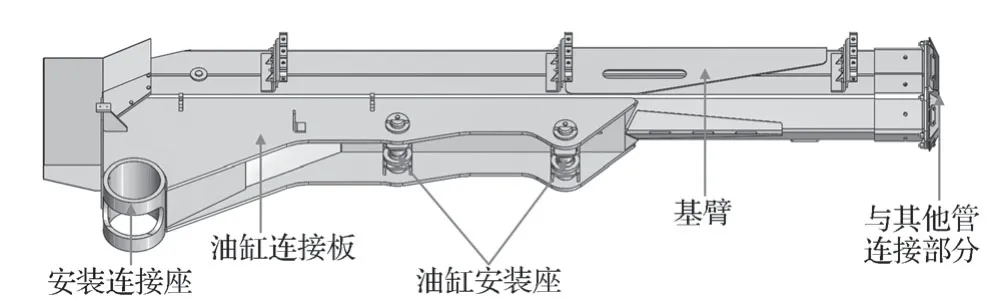
圖1 噴漿臺車機械臂大臂結構示意圖Fig.1 Schematic diagram of large arm structure of shotcreting trolley

如圖1所示，噴漿臺車機械大臂可分為臂管、安裝座連接軸和兩個油缸安裝座。機械臂具體型號為GL3515，其施工能力為35 m3/h。

由于噴漿臺車大臂結構復雜，主要由各種厚度的鋼板焊接而成。為簡化計算，只取噴漿臺車機械臂大臂的主要臂管部分進行有限元分析。其中測得噴漿臺車機械臂大臂的基臂長3 306 mm，寬274 mm，厚度為6 mm；油缸連接板長約2 180 mm，兩板間相距226 mm，板厚16 mm；油缸安裝座長120 mm，寬226 mm，板厚10 mm；安裝連接座半徑120 mm，板厚20 mm；與其他管連接部分長208 mm，寬274 mm，板厚14 mm。在HyperMesh中建立其有限元模型，如圖2所示。

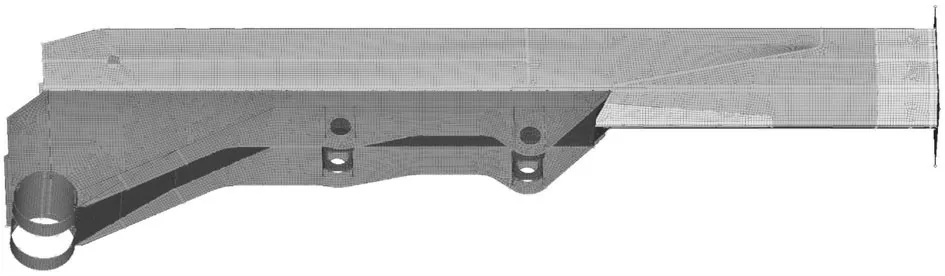
圖2 噴漿臺車機械臂有限元模型Fig.2 Finite element model of the shotcreting trolley mechanical arm

課題組主要使用shell單元對大臂基臂進行離散，對安裝座連接軸、兩個油缸安裝座以及右端桿連接部分結構用rigid單元進行模擬。機械臂大臂的材料為HG70高強度焊接結構鋼，其化學成份如表1所示。

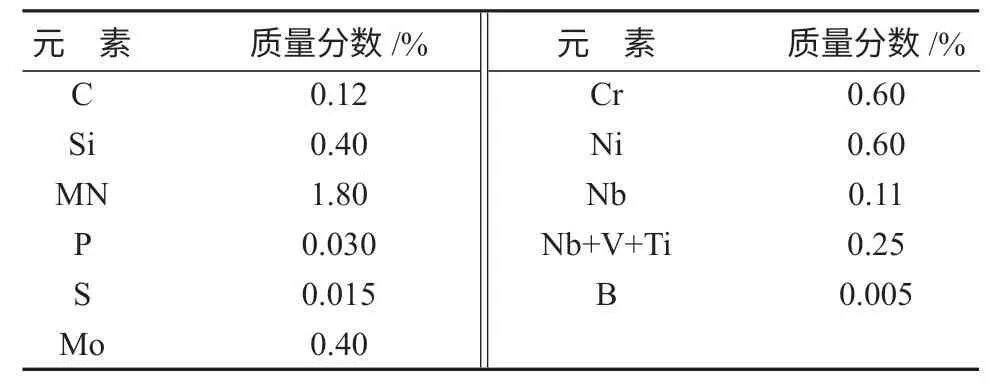
表1 HG70高強度焊接結構鋼化學成份Table1 Chemical composition of HG70 high strength welded structural steel

HG70高強度焊接結構鋼的力學性能指標如表2所示。

表2 HG70高強度焊接結構鋼力學指標Table2 Mechanical indexes of HG70 high strength welding structural st eel

該材料的密度為7 850 kg/m3，彈性模量為200 GPa，泊松比為0.3。經過測量，得出原噴漿臺車機械臂總體積為5.554e+07 mm3。由“質量=密度×體積”公式可得，原機械臂的質量為：7 850 kg/m3×5.554e+07 mm3≈436 kg。

1.2 剛強度分析

圖3所示為機械大臂在工作過程中的受力情況示意圖。

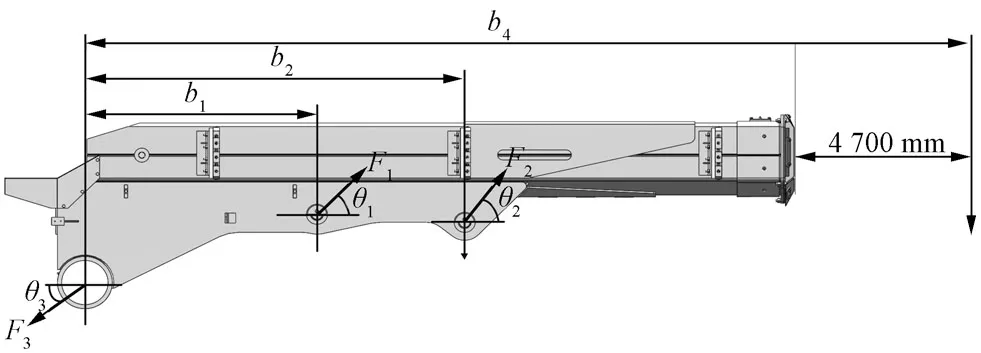
圖3 機械臂受力情況示意圖Fig.3 Schematic diagram of mechanical arm under force

機械大臂受到兩個斜向上的支撐力F1、F2，一個斜向下但方向不定的力F3，以及一個垂直向下的力F4的作用，在4個力的共同作用下，大臂保持平衡。以點A為基點，對大臂進行受力分析，可得：

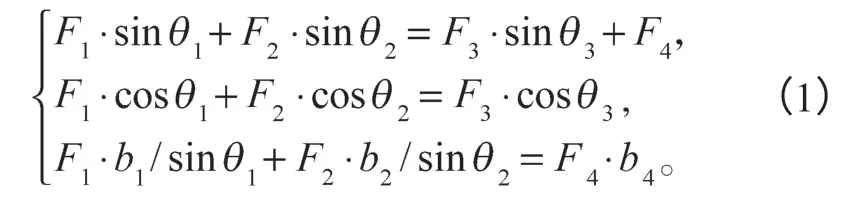
根據實際情況和計算要求，對機械臂建立一個工況。在安裝座連接軸所在面和兩個油缸安裝座所處圓孔處進行全方位約束。在大臂右側與機械臂其它臂管連接部分的不規則孔處建立rigid單元，將rigid單元沿x軸方向剛性平行移動4 700 mm，考慮到動載系數，于是在rigid單元上施加一個沿y方向向上的、大小為19 500 N×1.2倍的力。

通過計算求解得出該工況下的機械臂應力分布如圖4所示，其中圖b是對圖a中應力最大部分的放大細節。

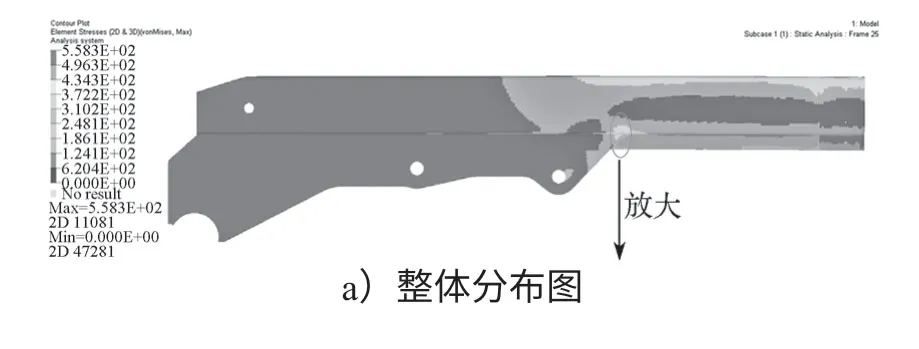
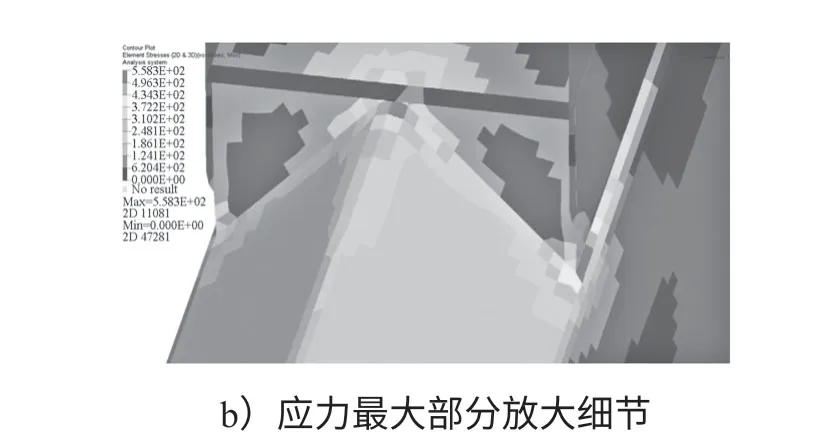
圖4 原機械臂應力分布圖Fig.4 Original mechanical arm stress distribution diagram

由圖可見，原機械臂所受應力最大部分主要集中在基臂和油缸連接板的接合處，最大應力達到了558.3 MPa，而油缸連接板部分所受應力很小，應力分布極其不均，因此對其進行拓撲優化很有必要。

1.3 模態分析

模態分析[9-10]是研究物體動力特性的一種方法，其中模態是指物體機械結構的固有振動頻率。其矩陣表達式為

其對應的特征方程為

式（2）（3）中：M為結構質量矩陣；

K為剛度矩陣；

ω為自由振動固有頻率。

求解出方程（2）即可求出系統的固有頻率和振型。由于單純機械激勵頻率[11]多在10 Hz 以內，在Optistruct中對機械臂進行模態分析，根據需要提取前6階模態結果，前6階模態頻率如表3所示。

表3 機械臂大臂的前6階頻率Table3 First 6 frequencies of the big arm of the manipulator arm

第1、3、4、6階模態的振型如圖5a～d所示。由圖可知第1階模態固有頻率為81.23 Hz，振型由左右擺動為主；第3階模態固有頻率為152.76 Hz，振型由上下擺動為主；第4階模態固有頻率為170.67 Hz，振型由整個機械臂振動，帶動機械臂大臂與其他管連接部分上下擺動；第6階模態固有頻率為179.55 Hz，振型由機械臂基臂靠近安裝連接座部分局部左右擺動。

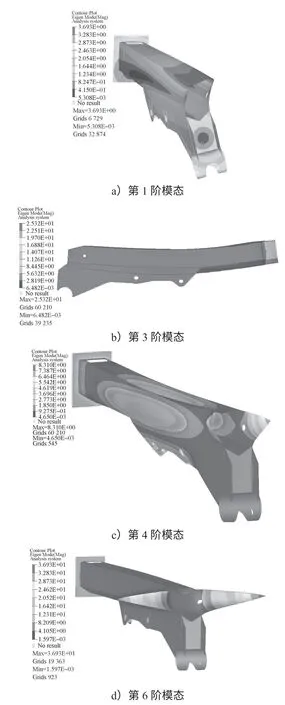
圖5 原機械臂模態分析圖Fig.5 Original mechanical arm modal analysis diagram

2 機械臂拓撲優化

2.1 目標與約束條件

拓撲優化是一種根據給定的負載情況、約束條件和性能指標，在給定的區域內對材料分布進行優化的一種結構優化方法。拓撲優化相較于尺寸優化和形狀優化，具有更多的設計自由度，從而能獲得更大的設計空間。

優化過程的數學模型如下。

設計變量：

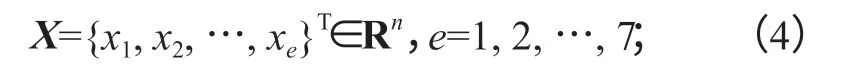
目標函數為

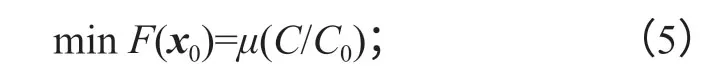
狀態變量為：

式（4）～（6）中：Rn為一個n維實歐氏空間，稱為設計空間；

C0為進行剛度優化時的最初拓撲值；

μ為權系數，取值區間為[0,0.1]；

V(x)為機械臂油缸連接板的設計部分的體積分數。

課題組在對機械臂進行工況處理時，在有限元模型上對安裝座連接軸所在面和兩個油缸安裝座所處圓孔處進行全方位約束。在大臂右側與機械臂其他臂管連接部分的不規則孔處建立rigid單元，將rigid單元沿x軸方向剛性平行移動4 700 mm，并施加一個沿y方向向上的19 500 N的力。以該工況下大臂柔度最小作為優化目標，以油缸連接板體積不超過原大臂總體積的0.2，且機械臂所受應力小于500 MPa 作為約束條件。在機械臂的尺寸優化中，以臂管厚度作為設計變量，在Hypermesh中，將機械臂的臂管按照所處位置及初始厚度分為7個組件。在Optistruct軟件中用0階方法進行優化計算，經過10次迭代計算后得到優化結果。

2.2 優化結果

經過10次迭代計算后的優化結果如圖6所示。

圖6 原機械臂10次迭代后的拓撲優化圖Fig.6 Topology optimization diagram after ten iterations of the original manipulator

圖6為單元密度分布圖，圖中油缸連接板內側部分單元密度值較低，說明此部分材料分布較為富余，在機械臂形貌的重新設計中，可以刪去以減輕機械臂的質量。與原機械臂相比，油缸連接板側板處有較大不同，原油缸連接板上部分不必要的筋板被刪除，原來的4 塊面板也變成了一塊面板加4 塊小三角形筋板的形式。

3 拓撲結構重設計及性能對比

3.1 結構重設計

由于拓撲優化完之后，以刪除單元為形式，導致大臂表面不光滑，或某些地方不連續，所以需要進行平整化處理。根據形貌優化后的結果對機械臂大臂進行重新設計，優化前后的機械臂結構對比圖如圖7所示。

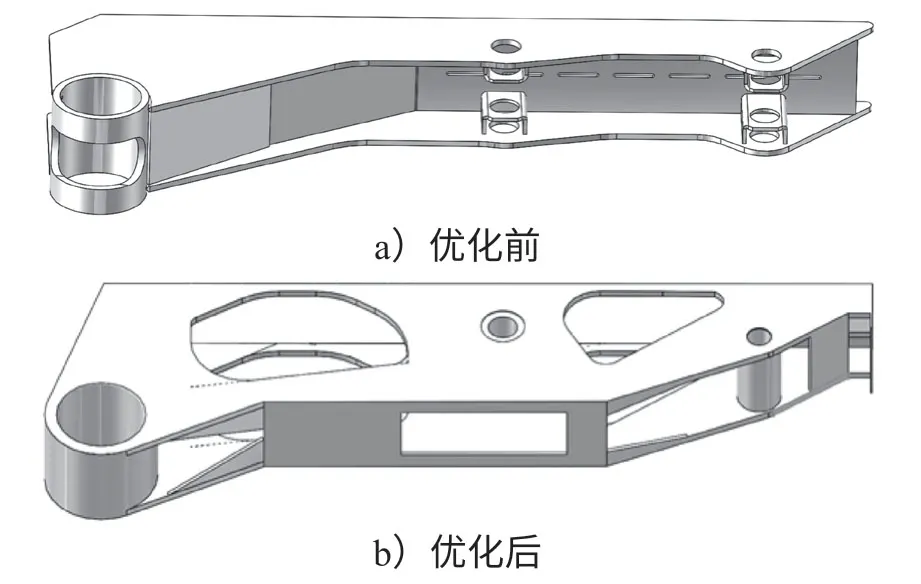
圖7 優化前后機械臂模型結構Fig.7 Model structure of the manipulator before and after optimization

由圖7可清晰看出機械臂優化前后油缸連接側板及3 塊面板的變化，刪去了油缸連接板側板處不必要的筋板，將3 塊面板減少成1 塊面板加4 塊小三角形筋板的形式。

通過測量機械臂優化前后的總體積，算得：

優化前機械臂質量為7 850 kg/m3×5.554e+07 mm3≈436 kg；

優化后機械臂質量為7 850 kg/m3×5.091e+07 mm3≈399 kg。

機械臂的質量由原來的436 kg 減少到399 kg，降幅超過8%，使機械臂結構更合理，同時也降低了制造成本。

3.2 優化前后性能對比

對優化后的機械臂進行靜力學和模態分析。優化后機械臂的最大應力由初始的553.8 MPa 減小到503.7 MPa，并且受力比原來更均勻。優化后機械臂的前6階模態如表4所示。

表4 優化后機械臂大臂的前6階頻率Table4 First 6 frequencies of the robot arm after optimization

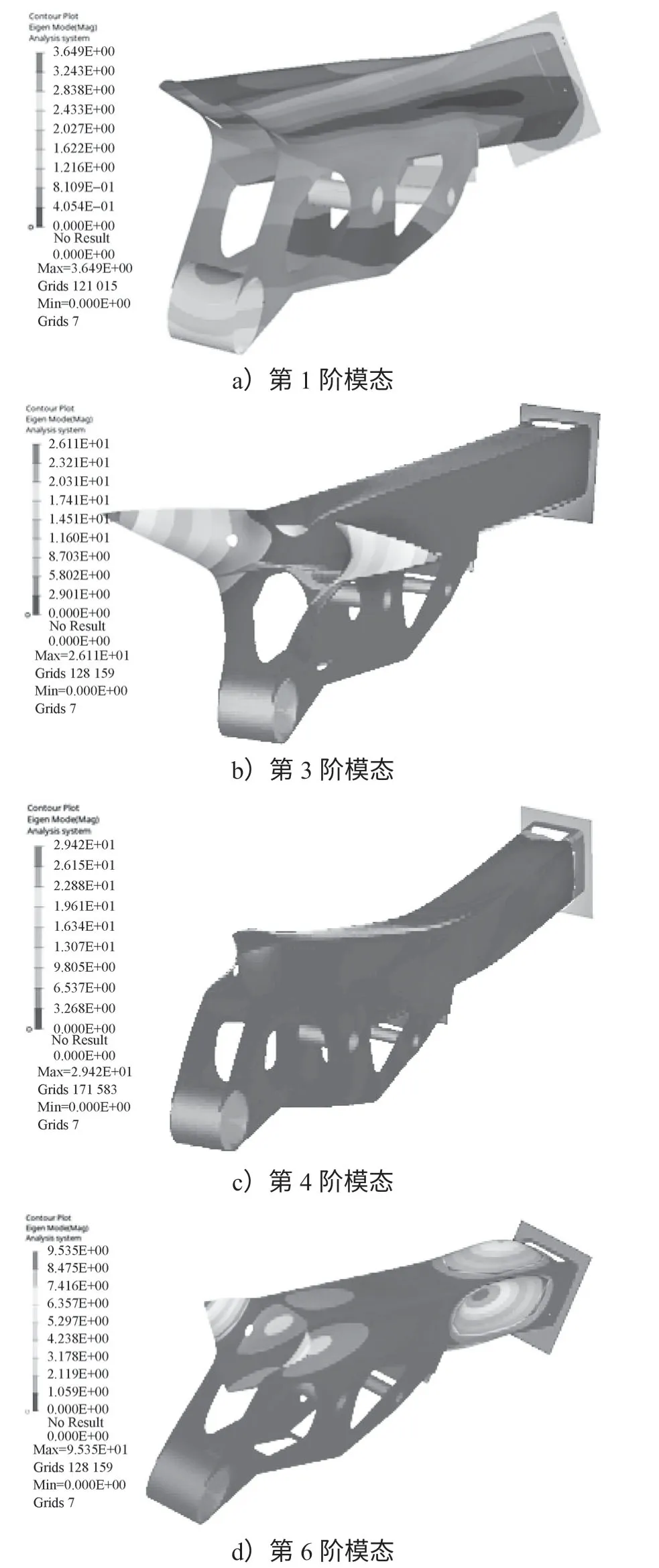
圖8 優化后機械臂模態分析圖Fig.8 Modal analysis diagram of the optimized manipulator

優化后的機械臂的模態分析圖如圖8所示。

由圖8中的4張圖可清晰看出第1、3、4、6階模態的振型。對比表3和表4可以得出，機械臂的頻率及振型都有較大的變化。從理論上來說，固有頻率2=剛度/質量,增加剛度會提高固有頻率。優化前后的機械臂固有頻率對比如表5所示，由表中數據對比可見新機械臂的第一階彈性模態固有頻率由原來的81.23 Hz 提高到89.09 Hz，固有頻率的提高代表著機械臂整體結構剛度得到了提升。提升機械臂的剛度能減少機械臂的變形和應力，從而對結構起到較好的保護作用。

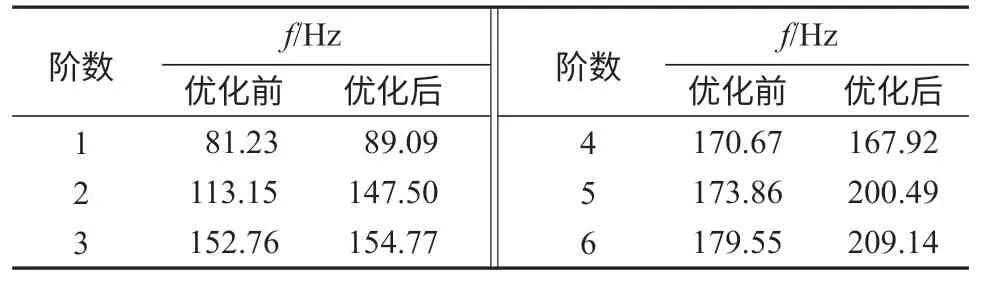
表5 優化前后機械臂大臂的固有頻率Table5 Natural frequency of the manipulator arm before and after optimization

優化前后機械臂所受應力大小如圖9所示。對比優化前后兩圖可以得出，機械臂的最大應力由553.8 MPa 減小到503.7 MPa，原機械臂所受應力最大部分主要集中在基臂和油缸連接板的接合處，經過優化后的機械臂所受應力最大部分集中于基臂上，并且受力比原來更均勻。

圖9 優化前后機械臂所受應力大小對比圖Fig.9 Comparison diagram of stress on mechanical arm before and after optimization

4 結語

本文建立了針對噴漿臺車機械臂大臂的有限元模型，并對其進行了靜態模態分析和拓撲優化。以柔度最小為優化目標，優化后的新機械臂質量減少了37 kg，減少了約8%的質量。第一階彈性模態固有頻率由81.23 Hz 提高到89.09 Hz，最大應力在規定工況下降低9%。綜上可看出，噴漿臺車機械臂大臂結構綜合靜態性能得到了較大的改善，為后期噴漿臺車機械臂的優化設計提供了理論基礎。