各向異性電介質二維無限域拉普拉斯方程定解問題

許景生

（嶺南師范學院 基礎教育學院，廣東 湛江 524037）

陳燊年、洪清泉等系統地研究了介質為各向異性（限于有且只有三個正交主軸方向的電介質）的電磁場[1]，其中各向異性電介質拉普拉斯方程的定解問題是各向異性電介質靜電場的基本問題之一。拉普拉斯方程的定解問題可分為有限域和無限域兩種情形，求解有限域拉普拉斯方程的方法有分離變量法、角基函數法、變分正則法和變分迭代法等，其中分離變量法較常用[2-5]；求解無限域拉普拉斯方程的方法有積分變換法、分離變量法等，其中積分變換法較常用[6]。分離變量法和積分變換法均可求解無限域拉普拉斯方程，但這兩種解法求得的解具有不同的數學形式。分離變量法求解無限域拉普拉斯方程，除了方程和邊界條件必須是齊次的之外，對區域的形狀也有明顯限制，要求空間區域的邊界面必須是正交曲面坐標系的坐標面；若空間區域是無限域的，本征值將過渡為連續譜，則求得的解及解中的展開系數用傅里葉積分表示。陳燊年等、李文略等應用分離變量法求解有限域拉普拉斯方程的定解問題[1，7-9]，但未涉及各向異性電介質無限域拉普拉斯方程的定解問題。李文略等研究了三維或二維無限域泊松方程的定解問題，其中涉及了應用積分變換的求解方法，但并未涉及驗證兩種解的等價性[10-11]。顧樵[12]分別應用分離變量法和積分變換法求解熱傳導穩定溫度場的拉普拉斯定解問題，并指出結果是等價的。受此啟發，本研究分別應用分離變量法和傅里葉變換法求解各向異性電介質二維無限域拉普拉斯方程的定解問題，并舉典型算例間接驗證所得解的等價性。

1 各向異性電介質二維無限域拉普拉斯方程定解問題的確定

設各向異性電介質1和電介質2有相同的主軸坐標系O- x1x2x3，坐標面O- x1x3為這兩種電介質的分界面，在分界面上方（x2＞0的區域）充滿各向異性電介質1(設ε11、ε22、ε33分別為電介質1沿著主軸坐標系x1軸、x2軸、x3軸的介電常數)，在x2≤0的區域充滿各向異性電介質2。電介質1所在的區域是無源的，且其中的電勢分布僅用O- x1x2平面即可確定，例如在電介質2中過x2軸并沿著x3軸方向放置一無限長的均勻帶電密度為λ的直導線，則該帶電直導線在電介質1中激發的電勢滿足二維無限域拉普拉斯方程的定解問題，該定解問題用方程組表示為

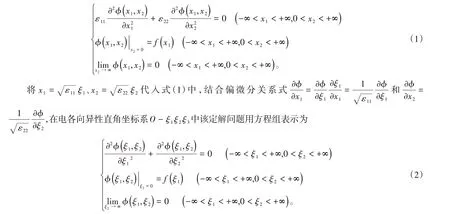
2 應用分離變量法求解二維無限域拉普拉斯方程的定解問題

設式（2）中的泛定方程有分離變量的形式解φ(ξ1,ξ2)= X(ξ1)Y(ξ2)，代入泛定方程中得到

式中，λ為分離常數。

當λ ＜0和λ= 0時，都會導致平庸解φ(ξ1,ξ2)= 0。當λ ＞0時，式（3）中第一個方程的通解為

式中，p、q為任意常數，由于受到式（2）中自然邊界條件的約束，故p= 0。

將式（4）和（5）代入形式解φ(ξ1,ξ2)= X(ξ1)Y(ξ2)中，得到泛定方程的解

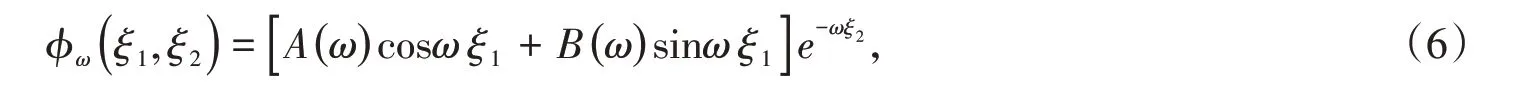
式中，A(ω)= aq，B(ω)= bq。因為泛定方程是線性的，對式（6）進行疊加構成一般解，因為ω是連續變化的，所以一般解是對ω的連續積分，得

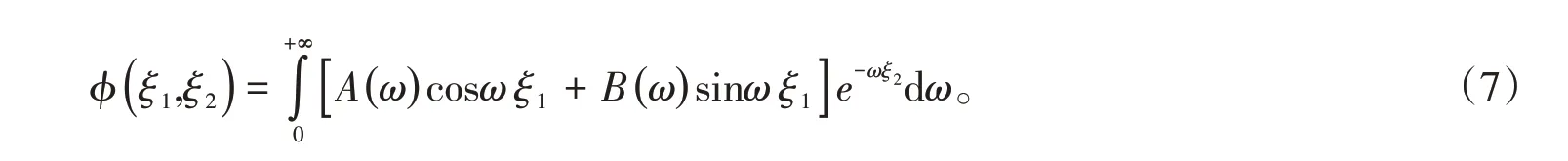
一般解須滿足式（2）中的第一類邊界條件，有

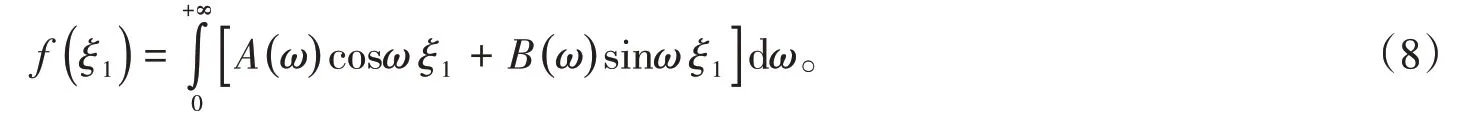
可知，式（8）為邊界函數f(ξ1)的傅里葉積分表示式，可得展開系數

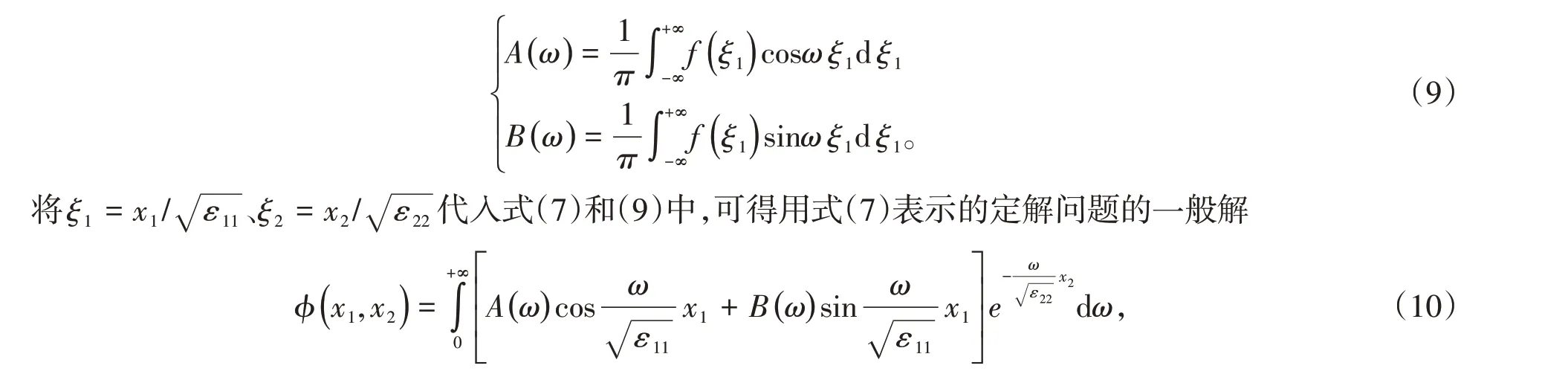
式中，展開系數為

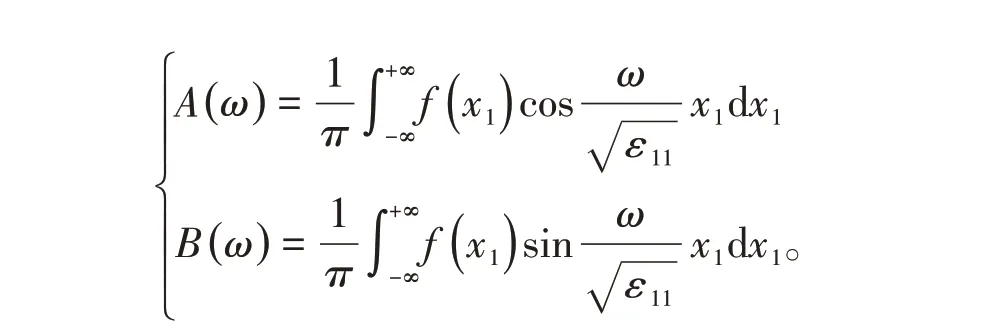
由求解的過程可知，因為分離常數λ是連續的，所以求解的過程不出現分立的本征值和相應的本征函數，解是用連續積分（含傅里葉積分）表示的。

3 應用傅里葉變換法求解二維無限域拉普拉斯方程的定解問題

由定義域-∞＜ξ1＜+∞，可對式（2）取關于ξ1的傅里葉變換

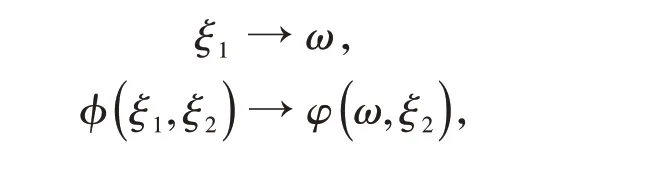
有

式（11）中泛定方程的通解為

式（12）須滿足式（11）中的第一類邊界條件，故有φ(ω,0)= F(ω)= C，將其代入式（12）中，得

對式（13）作傅里葉反變換

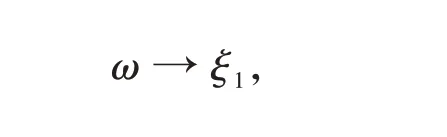
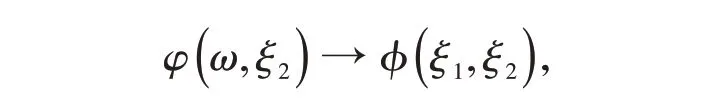
有

式中，“*”號表示傅里葉卷積。應用傅里葉變換法求解該定解問題時，所得的解用傅里葉卷積表示。

4 列舉算例間接驗證解的等價性

應用分離變量法或傅里葉積分法求解式（1）表示的各向異性電介質二維無限域拉普拉斯方程定解問題，所得的解用式（10）或式（15）表示，顯然解的具體數學形式不一樣。由靜電場的唯一性定理可知，這兩種解必然是等價的。現舉三個典型的例子間接驗證解的等價性。

（Ⅰ）設f(x1)= 0，將f(x1)代入式（10）中，有A(ω)= B(ω)= 0，φ(x1,x2)= 0；對于式（15）而言，f(τ)= 0 即是f(x1)= 0，將其代入式（15）中，亦可得φ(x1,x2)= 0。

對應這種情形的物理模型可以是各向異性電介質1 和電介質2 的分界面處放置接地的無限大導體平面。由所得結果φ(x1,x2)= 0可知，接地導體平面上方電介質1所在的區域是靜電屏蔽的，倆解是等價的，符合物理客觀事實。

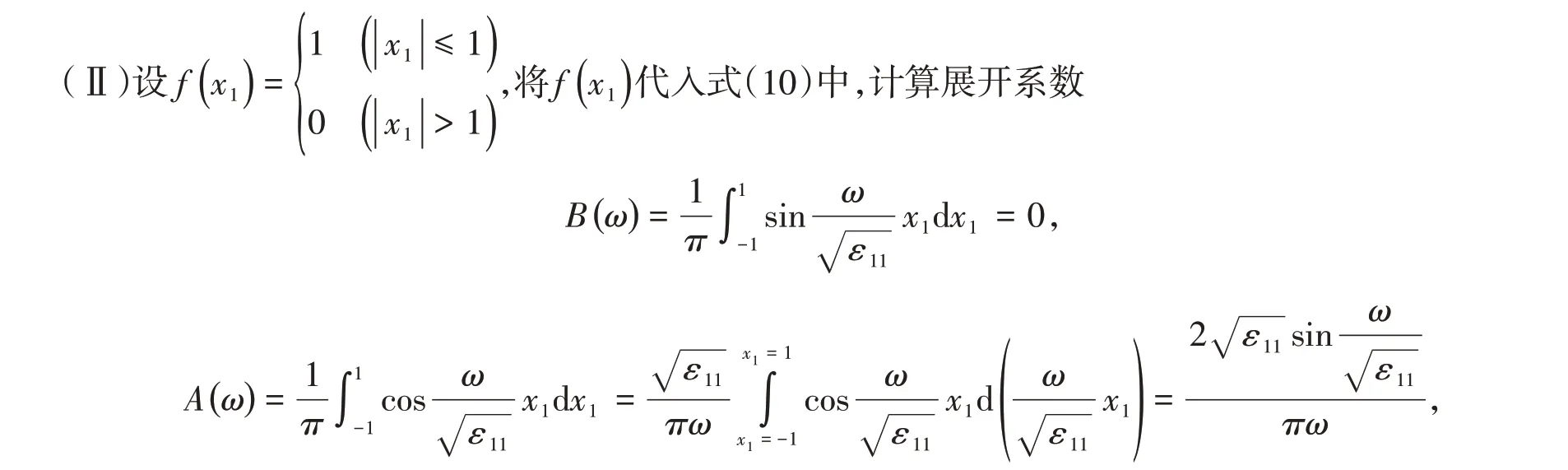
則解為

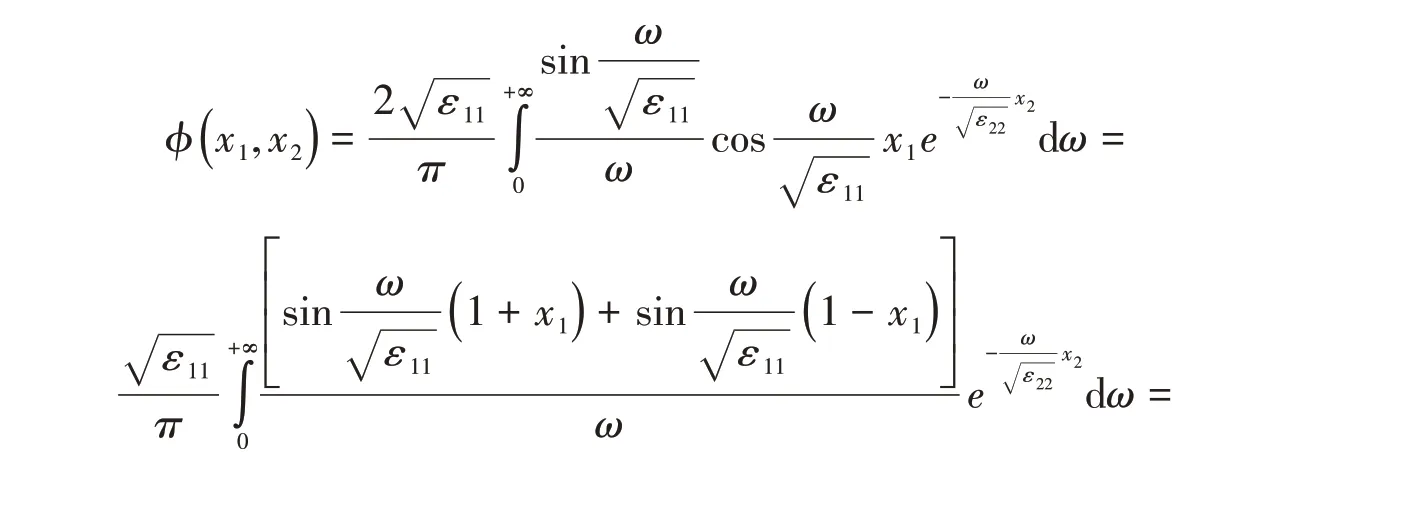
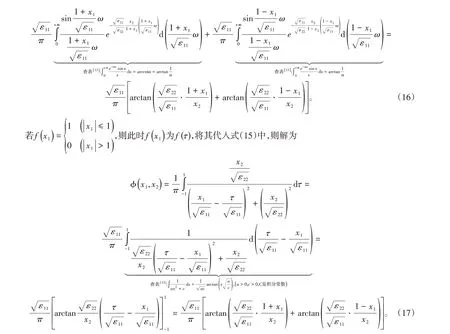
可知式（16）和（17）表示的解是相等的。對應這種情形的物理模型可以是各向異性電介質1和電介質2的分界面處放置了三片無限大的導體平面，分別位于( - ∞＜x1＜-1)和(1 ＜x1＜+∞)區域的導體平面接地，而位于( - 1 ≤x1≤1)區域的導體平面是不接地的等勢體。由所得的結果可知，無限大平面上方電介質1所在的區域不能實現靜電屏蔽，電勢分布由式（16）或（17）描述。

則解為

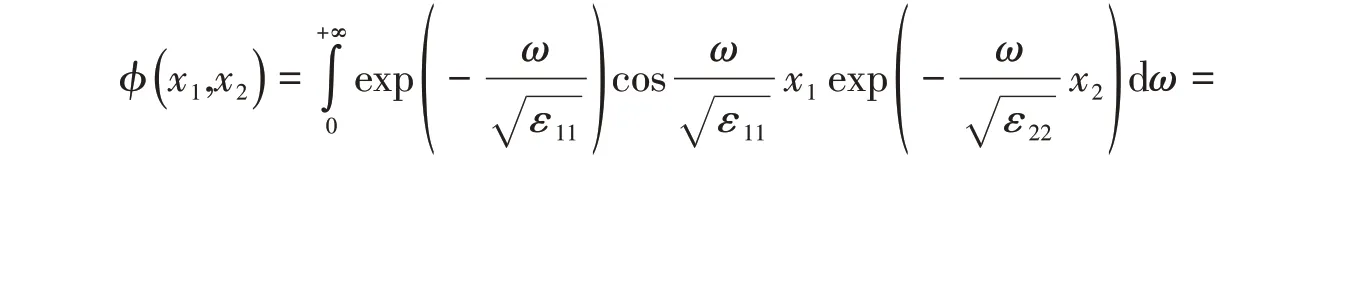
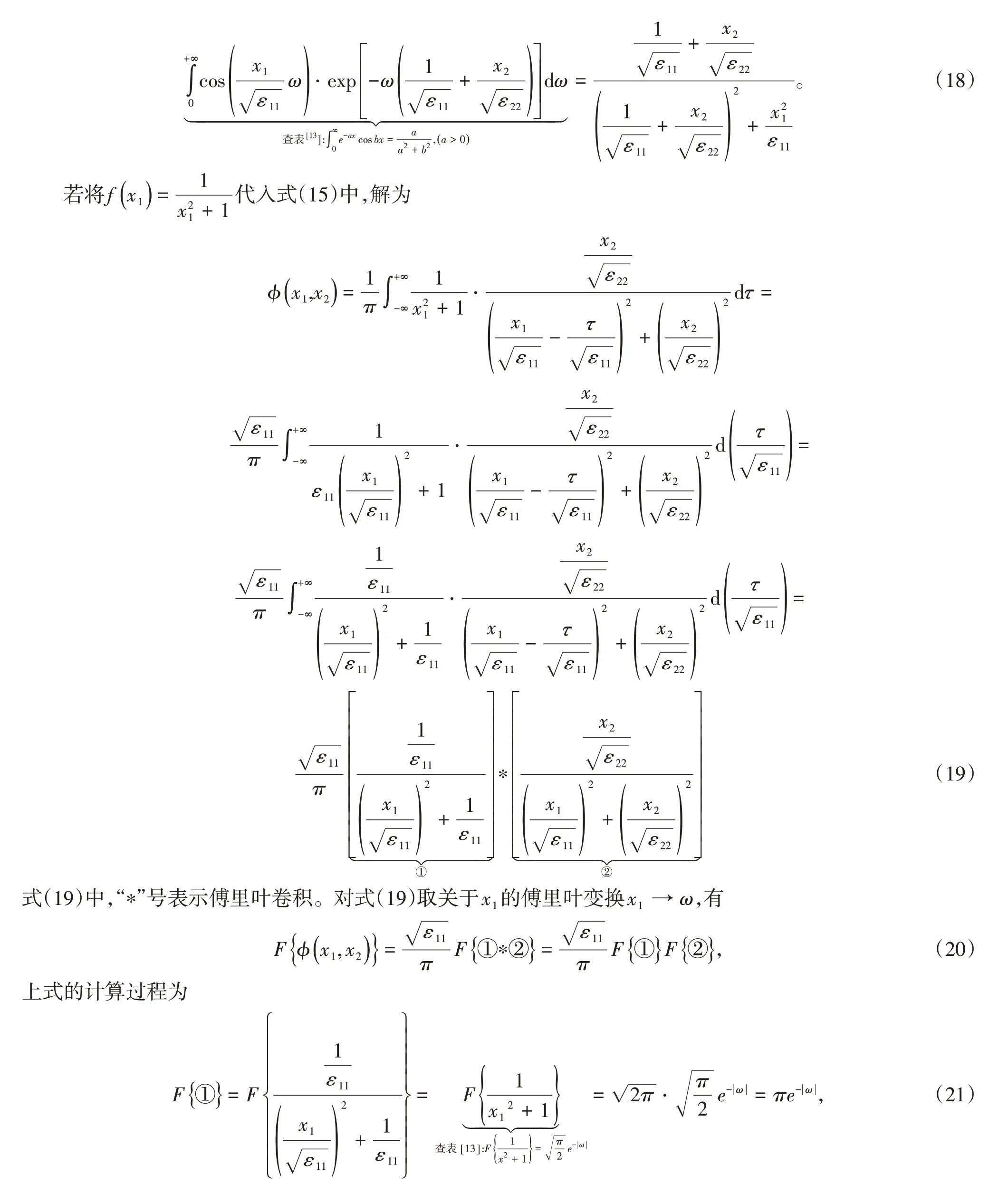
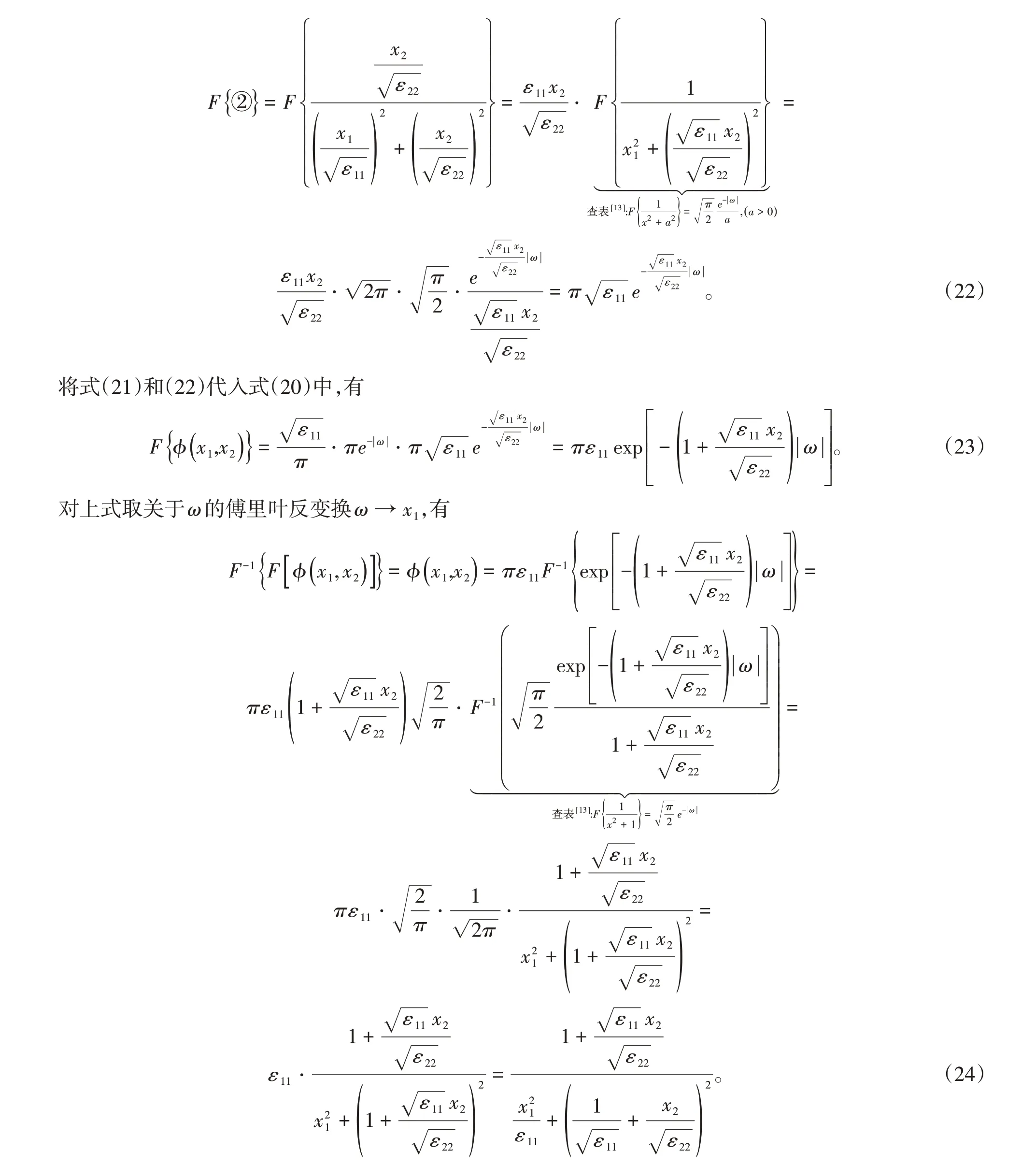
可知式（18）和式（24）表示的解是相等的。對應這種情形的物理模型可以是在各向異性電介質1和電介質2的分界面下方（電介質2所處的區域）有電荷分布，此時電介質的分界面不再是等勢面，分界面處的電勢關于主軸x2軸對稱，且電勢隨著遠離主軸x1軸而衰減。電介質分界面上方區域無源，電勢滿足拉普拉斯方程，電勢分布由式（18）或式（24）描述。

綜合以上的計算過程可知，在求解各向異性電介質二維無限域拉普拉斯方程定解問題時，總是先將主軸坐標系中描述的定解問題[由方程組（1）表示]通過變量代換轉化為在電各向異性坐標系中來描述[由方程組（2）表示]，求得解之后再通過變量逆變換得到在主軸坐標系下的解，這是研究各向異性電介質泊松方程（或拉普拉斯方程）常用的方法。由靜電場的唯一性定理可知，分別應用分離變量法和傅里葉變換法求得的解是等價的。以上所舉例子中表示第一類邊界條件的函數f(x1)有取零的特殊情形、有取分段函數的情形也有取連續函數的情形，且均給出了與這三種情形相對應的物理模型，由此可推斷解的等價性具有普遍性也符合物理客觀事實。若要直接證明兩種數學形式的等價性，則需證明式（7）與式（14）是相等的，即

觀察式（25）可知，要分別求得等號左右兩邊廣義積分的結果，可拓展至復平面上進行計算，但由于函數f(ξ1)或f(η)的具體形式不可知，因而無法確定被積函數的奇點，無法應用留數定理求得結果；若函數f(ξ1)或f(η)的具體形式已知，則相當于給出了特例，即是文中的間接驗證其等價性的方法。

若兩各向異性電介質分界面上方和下方的區域分別填充的是介電常數分別為ε1和ε2的各向同性電介質，則文中描述的各向異性電介質二維無限域拉普拉斯方程的定解問題可過渡為各向同性電介質二維無限域拉普拉斯方程的定解問題。若將ε11= ε22= ε33= ε1代入式（10）中，可應用分離變量法求得

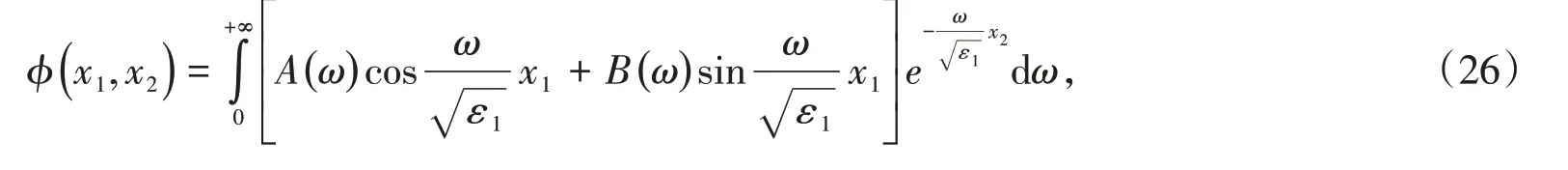
式中，展開系數為

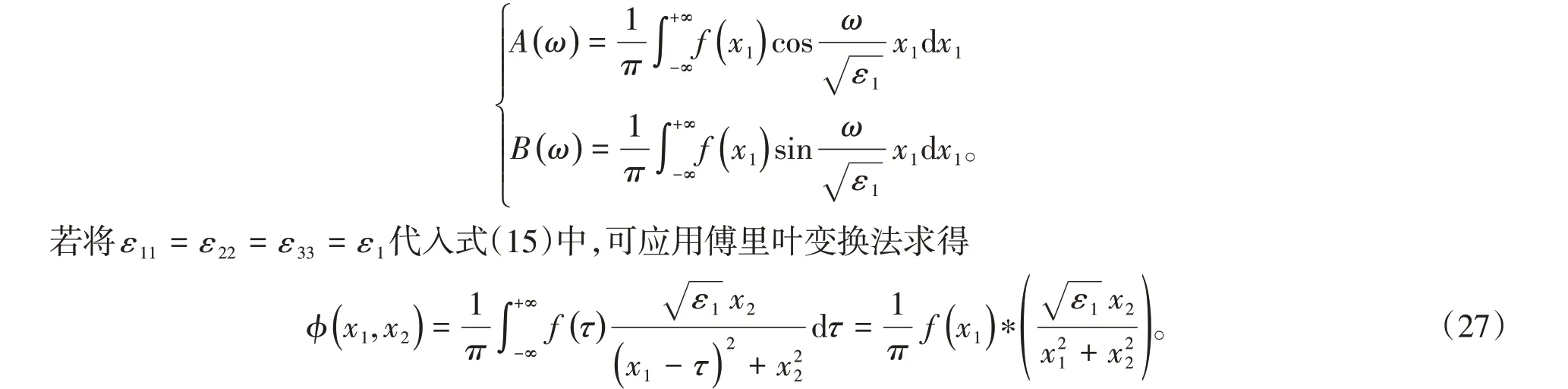
式（26）和式（27）是等價的，可用算例間接驗證，計算過程在此不再贅述。