高速沖床肘節機構的運動特性研究*

李義強，戴惠良*，張治軍，彭進利

(1.東華大學 機械工程學院,上海 201620；2.浙江帥鋒精密機械制造有限公司,浙江 嘉興 314300)

0 引 言

高速沖床已有近百年的發展史，應用范圍廣泛，其傳動機構從曲柄滑塊機構演變為各種各樣的多連桿機構，如肘節機構。

傳統高速沖床多采用對心曲柄滑塊機構，被廣泛用于板材沖壓，其滑塊運動多為正弦規律[1]。肘節式高速沖床在沖壓時下死點速度低、急回特性好；沖壓過程產生的振動以及沖擊都較小[2]。此前很多學者對沖床傳動機構進行了運動特性分析。袁丁益等[3]運用ADAMS軟件對多連桿壓力機傳動機構運動過程的特性進行了分析；蔡玉強等[4]采用聯立約束法通過Matlab/Simulink對曲柄滑塊機構進行了建模并仿真分析了其運動特性；GAWANDE S H等[5]對肘桿夾緊機構進行了數學建模及優化設計，并借助計算機輔助分析軟件進行了受力分析；BALASUBRAMANYAM C等[6]采用閉環法對雙肘桿機構的運動以及連桿長度對機構停留時間的影響進行了研究；張慶飛等[7]用解析法研究了高速沖床傳動機構存在慣性力的原因；鄺衛華[8]運用幾何分析法對沖床滑塊機構進行了動力學特性的研究。

很多學者對沖床傳動機構的運動特性進行了分析，但大多數的研究是對傳統的曲柄滑塊機構進行分析，很少有研究人員對肘節機構進行系統研究。帥鋒公司主要沖床產品為曲柄式和肘節式兩種，曲柄滑塊機構因其本身結構的限制，難以獲得良好的沖壓曲線且振動較大。為了滿足企業需求，迫切需要了解肘節式傳動機構的運動特性。

本研究將結合帥鋒公司Best-30沖床，以肘節機構為研究對象，進行運動原理的推導驗證、運動曲線仿真及影響因素探究，并實地搭建測試平臺，測試下死點動態精度，獲得滑塊運動曲線，探究肘節機構的運動特性。

1 肘節機構理論分析

1.1 肘節機構原理分析

高速沖床傳動機構運動簡圖如圖1所示。

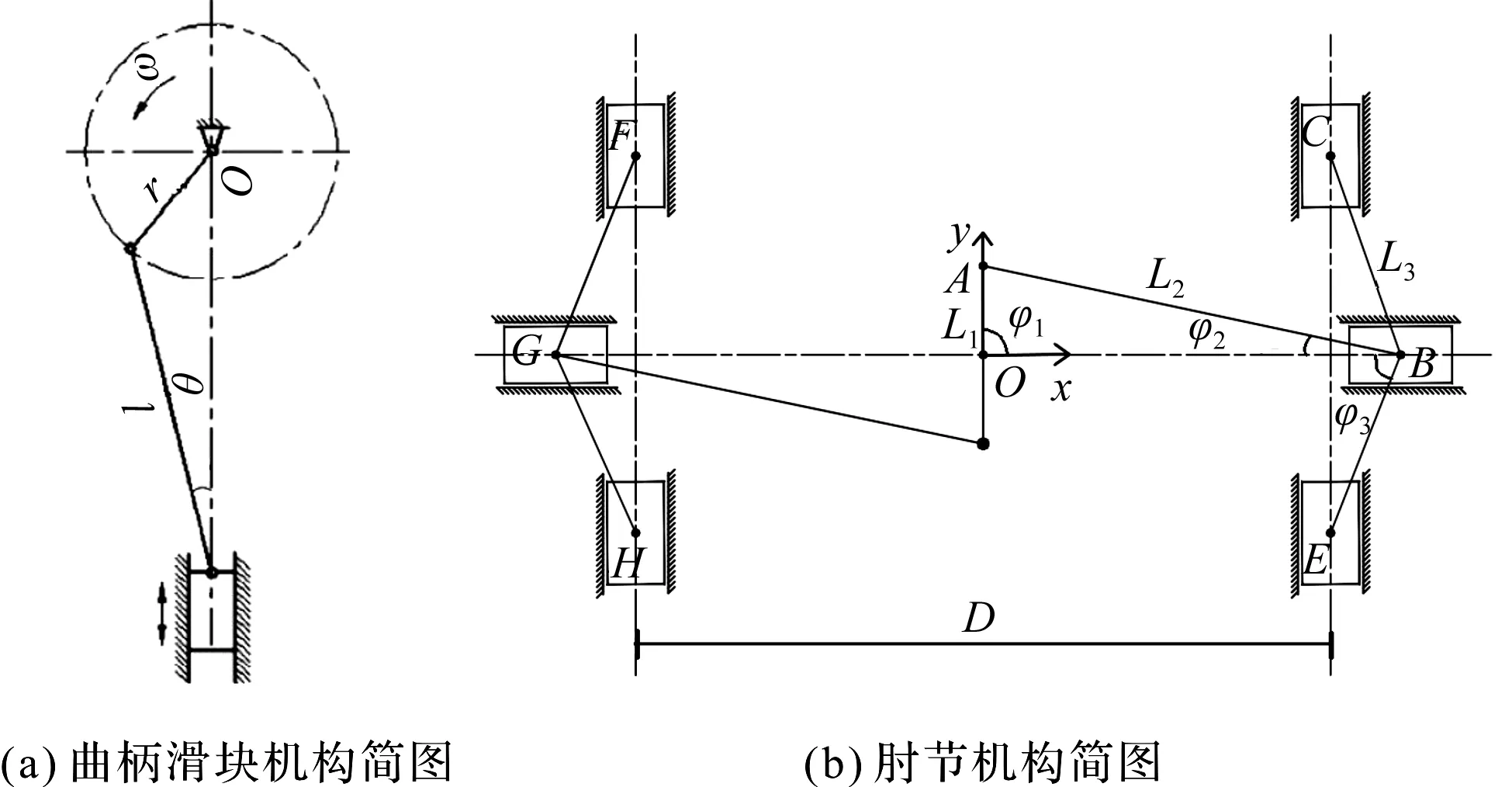
圖1 傳動機構運動簡圖r—曲柄半徑；l—連桿長度；OA—曲柄半徑；AB—連桿；BC，BE—上、下連桿，BC=BE；B，G—輔助滑塊；C，F—動平衡塊；E，H—沖壓滑塊；D—導柱中心距離

由圖1可知，肘節機構是在橫置的曲柄滑塊機構基礎上增加了上、下連桿及滑塊。肘節機構上下、左右均對稱，連桿AB與滑塊B構成橫置的曲柄滑塊機構，通過輔助滑塊B的平動帶動滑塊C、E豎直運動以完成沖壓過程。

1.2 位移、速度、加速度方程

設OA角速度為ω，AB、BC、BE的長度為L1、L2、L3，OA、AB、BE的角位移為φ1、φ2、φ3，其中：φ1—角速度ω的旋轉角位移。

(1)

(2)

式中：XB—輔助滑塊B的水平位移。

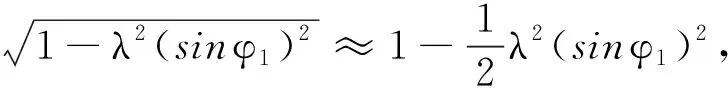
(3)

即滑塊E的位移SE、速度vE、加速度aE分別為：

(4)

(5)

(6)

肘節機構滑塊的運動參數SE、VE、aE都是φ1的函數，滿足關系式Y=f(φ1)，所以給定曲柄角位移φ1的大小，將D/2、L1、L2、L3代入即可得滑塊位移、速度、加速度。

1.3 靜力分析

曲柄轉動時，運動構件的慣性力(力矩)都較大，需要進行受力分析。

筆者依據達朗貝爾原理對肘節機構各部件進行動態靜力學分析，機構各部件靜力分析圖如圖2所示。

圖2 機構各部件靜力分析圖F1,2ax，F1,2ay，F1,2bx，F1,2by—曲柄在x、y軸上力的分量；Md—平衡力矩；m1—曲柄質量；F2a,IIIax，F2a,IIIay，F1,2ax，F1,2ay，F2b,IIIbx，F2b,IIIby，F1,2bx，F1,2by—連桿作用力在x、y軸上的分解力；m2a，m2b—連桿質量；F2a,IIIax，F2a,IIIay，FIIIa,3ax，FIIIa,3ay，FIIIa,4ax，FIIIa,4ay，F2b,IIIbx，F2b,IIIbay，FIIIb,3bx，FIIIb,3by，FIIIb,4bx，FIIIb,4by—輔助滑塊作用力在x、y軸上的分解力；FIIIa,0，FIIIb,0，Mra，Mrb—輔助滑塊所受約束反力(力矩)；mIIIa，mIIIb—輔助滑塊質量；FIIIa,3ax，FIIIa,3ay，F3a,IIx，F3a,IIy，FIIIb,3bx，FIIIb,3by，F3b,IIx，F3b,IIy—上連桿作用力在x、y軸上的分解力；m4a，m4b—上連桿質量；FIIIa,4ax，FIIIa,4ay，F4a,Ix，F4a,Iy，FIIIb,4bx，FIIIb,4by，F4b,Ix，F4b,Iy—上連桿作用力在x、y軸上的分解力；m4a，m4b—上連桿質量；F4a,Ix，F4a,Iy，F4b,Ix，F4b,Iy—沖壓滑塊作用力在x、y軸上的分量；F沖x，F沖y，M沖—沖壓滑塊所受沖力(力矩)；F3a,IIx，F3a,IIy，F3b,IIx，F3b,IIy—平衡滑塊作用力在x、y軸上的分量；FII0，Mrn—平衡滑塊所受沖力(力矩)；mI，mII—沖壓、平衡滑塊質量

考慮重力忽略摩擦力，分別對各構件進行動態靜力學分析。

由圖2得，各構件力平衡方程分別為：

(7)

(8)

(9)

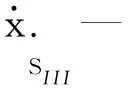
(10)

(11)

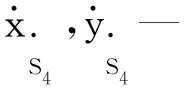
(12)

(13)

由以上分析可得，肘節機構可列出一個方程組數與作用力數相等的33元線性方程組：

AR=B

(14)

式中：A—力(力矩)系數矩陣；R—作用力(力矩)；B—慣性力(力矩)或重力等。

未知量與方程組數相等，方程有確定的唯一解，可運用Matlab求解具體的作用力(力矩)數值。

2 虛擬樣機模型

虛擬樣機建模包括幾何模型以及各構件的約束，各零部件約束由軟件直接定義，零部件形體細節部分無需完全一致，只要保證實際構件的質量、慣性屬性與幾何模型一致即可[9-10]。隨著加工精度、速度要求的變高，分析時不能忽略彈性變形[11]，因此需要對變形較大的構件進行柔性建模。

根據文獻[12]，肘節機構在沖壓過程中連桿受力復雜，彈性變形與彎曲變形均存在，所以在分析時須將連桿視為柔性體考慮。ADAMS中柔性體是用有限的離散結點來近似表示物體自由度[13]，直接運用ADAMS創建連桿柔性體模型并替換。

肘節機構模型圖如圖3所示。

圖3 肘節機構模型圖

3 肘節機構仿真分析

3.1 運動學與動力學分析

本文以滑塊行程25 mm，行程次數700 spm為約束條件，確定曲柄滑塊機構的尺寸為：r=12.5 mm，l=137.5 mm；確定肘節傳動機構的各桿件尺寸為：L1=25 mm,L2=260 mm,L3=150 mm,D=390 mm,λ≈0.1。利用ADAMS/view進行運動仿真，曲柄角速度取700 r/min，設置仿真時間為0.05 s，仿真步數為1 000步，初始位置為曲柄轉角φ1等于0。

動不平衡問題是桿組機構的固有特性，對桿組末端執行機構的運動精度影響較大。因此，筆者在運動學分析基礎上，設置邊界條件step(360 d*time)，對肘節機構各連桿進行動力學分析。設滑塊質量為600 kg，忽略其余桿件質量，僅考慮豎直方向受力。

曲柄滑塊機構、肘節機構運動曲線以及曲柄旋轉一周各連桿的動力學分析如圖4所示。

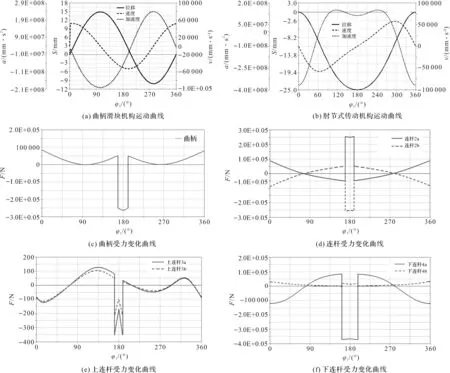
圖4 肘節機構仿真分析圖

高速沖床性能的優劣由滑塊的位移、速度、加速度表征[14-15]。

由圖4(a)可得，曲柄運動曲線基本遵循正弦規律，區別在于相位不同。滑塊的最大速度值5.17×104mm/s，下死點加速度即最大加速度值為2.4×108mm/s2；速度、加速度曲線呈周期變化，無急回特性。

由圖4(b)可得，在相同條件下肘節機構有明顯的急回特性，去程與回程角度比為2 ∶1。下死點速度變化緩慢,最大速度為5.86×104mm/s，最大加速度為3.68×108mm/s2,下死點加速度為1.13×108mm/s2，相比曲柄機構速度幅值增大了13.34%，下死點加速度值減小了52.92%。

由圖4(c～f)可得，當曲柄轉角在160°～ 200°范圍時，即滑塊在下死點附近時，機構中各桿件受力突變且幅值最大。曲柄力值為2×105N；兩連桿力值約為2.5×105N；兩上連桿力值存在突變，峰值分別為200 N，400 N；兩下連桿受力相差較大，峰值分別為3.5×105N，0.3×105N。

分析各桿件受力情況，其中連桿受力波動最大，較易損壞；下連桿中的軸向力波動明顯，力值相差較大，表明載荷主要作用對象是下連桿。因此應注意與下連桿相連接的滑塊導柱的強度問題。

3.2 影響因素分析

高速沖床曲柄的半徑、轉速對滑塊的運動特性有直接的影響，因此有必要對其展開研究。

Best-30沖床的行程等于曲柄半徑，當曲柄半徑分別取值15 mm、20 mm、25 mm、30 mm、35 mm時，得到不同曲柄半徑滑塊的運動曲線。

Best-30沖床曲柄最大轉速為1 200 r/min，考慮到設備使用壽命，實際沖壓速度應在最大速度的80%以內，即不超過960 r/min。在速度允許范圍內以25 mm行程沖床為例，筆者選取500 r/min、600 r/min、700 r/min、800 r/min、900 r/min 5種工作轉速進行分析。

曲柄半徑、轉速對滑塊運動影響分析曲線如圖5所示。

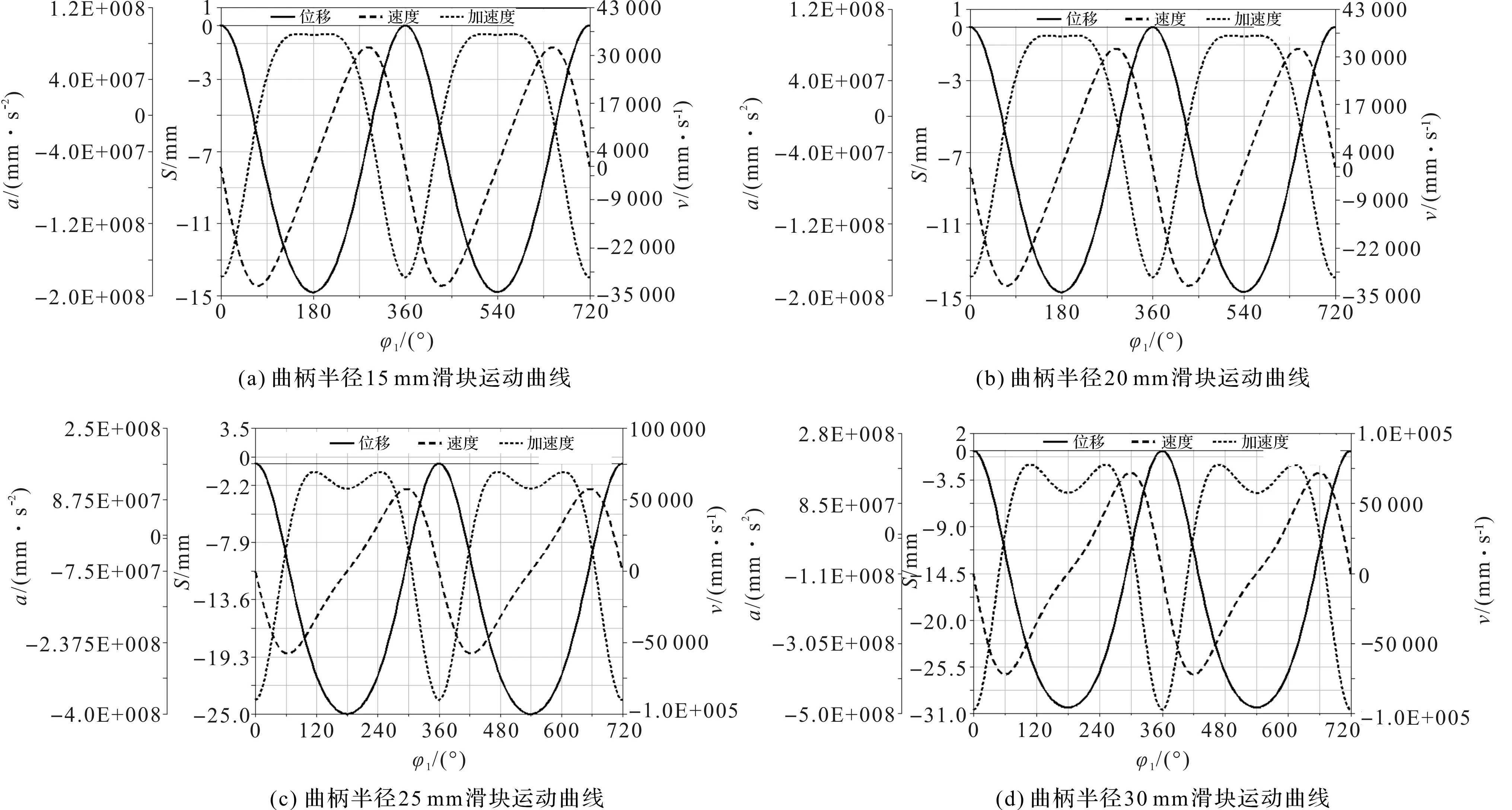
圖5 曲柄半徑、轉速對滑塊運動影響分析曲線

由圖5(a～e)可得，隨著曲柄半徑增加，滑塊行程不斷增大且與曲柄半徑相等，滑塊位移曲線的底部逐漸隆起即表明下死點的沖壓精度有所降低；滑塊速度、加速度波動變大，曲柄半徑為35 mm時，速度波動最大，下死點加速度降幅也最大。

由圖5(f～h)可得，隨著速度增大，位移曲線開口有微小緊縮，運動誤差有所增大，與理想狀態相比，位移誤差分別為0.017 mm、0.019 mm、0.020 mm、0.022 mm、0.025 mm。

當曲柄轉速增大，下死點附近速度曲線的斜率越來越大且速度、加速度峰值也變大，速度峰值增長率均在13%以上，加速度峰值增長率在22%以上，下死點加速度增長率在20%以上。在相同周期內，速度、加速度的最值之差逐漸變大，下死點加速度值先下降后上升的趨勢越來越明顯。

4 試驗及結果分析

4.1 測試平臺的搭建

本文用微米級帶表卡尺調平沖壓滑塊，測試儀器為日本理研RM-72型檢測儀，傳感器為RS-833H。通過自制夾具將測試探頭、傳感器固定在工作臺上。沖壓運動帶動滑塊進行上下運動，通過探頭和傳感器之間的距離變化來表征下死點變化。

4.2 結果分析

下死點動態精度測試結果如圖6所示。

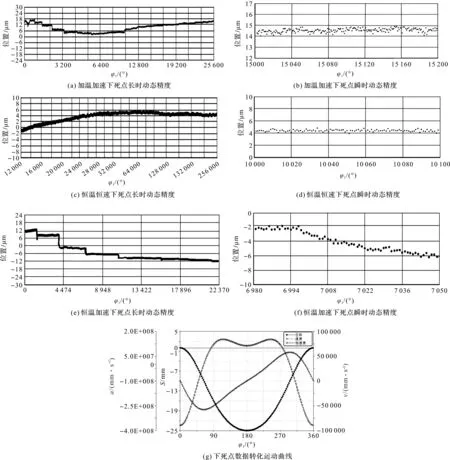
圖6 下死點動態精度測試圖

從圖6(a～b)中可以看出：沖床低速運轉達到熱平衡后，以恒定速度900 r/min運行3 h，加溫加速狀態下死點的長時位置誤差為15.374 μm，瞬時動態精度為1 μm。

從圖6(c～d)中可以看出：沖床恒速700 r/min、恒溫25 ℃運行2 h后，達到熱平衡，恒溫恒速狀態下死點的長時位置誤差為7.881 μm，瞬時動態精度為1 μm。

從圖6(e～f)中可以看出：沖床恒溫25 ℃、速度為100 r/min狀態下運轉至熱平衡狀態，分別以500 r/min，600 r/min，700 r/min，800 r/min，900 r/min速度運轉不低于5 min，恒溫加速狀態下死點的動態精度為26.111 μm，瞬時精度為4 μm。3種狀態的下死點精度允差均滿足GB/T29548-2013中規定的精密等級沖床的要求，這表明肘節式高速沖床具有較好的運動特性，具有較高的零件加工精度，符合設計需求。

下死點精度允差值如表1所示。

表1 下死點精度允差值

滑塊運動曲線圖是通過下死點測試儀器獲取的數據分析整理而成。

對比圖4(b)與圖6(g)得，滑塊位移為24.984 mm，與理論位移25 mm的誤差為0.016 mm，吻合度為99.94%；滑塊的最大速度值約為5.69×104mm/s，與仿真結果相差700 mm/s，吻合度為98.78%；最大加速度值約為3.63×108mm/s2，下死點加速度值約為1.15×108mm/s2，分別與仿真結果相差5×106mm/s2和2×106mm/s2，吻合度分別為98.64%和98.26%。

這表明了高速沖床肘節機構的設計合理性，也驗證了仿真結果的正確性。

5 結束語

本研究采用桿組分析法及靜力分析法推導肘節機構的運動方程和桿件受力情況，運用ADAMS軟件對其進行了運動學和動力學分析，并通過測試數據對仿真結果進行了驗證。

研究結果表明：

(1)與曲柄滑塊機構相比，肘節機構運動規律更理想，急回特性更好，回程時間約為去程時間的1/2；其在下死點附近的速度波動更小、加速度值下降約52.9%，下死點的停留時間更長，沖壓穩定性更好；

(2)肘節機構的曲柄半徑、轉速過小或者過大，都會導致滑塊運動特性變差，在設計或使用時應合理選取；

(3)肘節機構的測試結果與仿真結果吻合度在98%以上，下死點精度達到精密級沖床允差的要求。