基于斯塔克伯格博弈的邊緣協同計算研究

黎作鵬 王浩翔

摘? 要： 小型基站（Small?cell base stations，SBSs）被認為是邊緣計算環境中重要的組成部分。但由于自身計算資源有限，當計算工作負載過大時，為用戶提供的服務質量將面臨重大的挑戰。因此，針對小型基站間協同計算展開研究。首先，以最優化小型基站的個人效用為目標，結合多主多從斯塔克伯格（stackelberg）博弈模型，提出一種可實現小型基站間協同計算的算法。然后，通過循環迭代的方式求解小型基站之間非合作博弈的納什均衡解。最后，通過Matlab進行實驗，驗證了該算法的可行性和有效性。

關鍵詞： 小型基站; 邊緣計算; 協同計算; Stackelberg博弈; 納什均衡; 仿真分析

中圖分類號： TN929?34? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標識碼： A? ? ? ? ? ? ? ? ? ? ? 文章編號： 1004?373X（2020）14?0079?04

Research on edge cooperative computing based on Stackelberg game

LI Zuopeng1，2， WANG Haoxiang1，2

（1. School of Information and Electrical Engineering， Hebei University of Engineering， Handan 056038， China;

2. Hebei Key Laboratory of Security Information Perception and Processing， Hebei University of Engineering， Handan 056038， China）

Abstract：The small?cell base stations （SBSs） are considered as an important part of the edge computing environment. Since SBSs′ own computing resources are limited， the service quality provided to users will be faced with major challenges when the computing workload is too large. Therefore， the collaborative computing between SBSs is studied. With the goal of optimizing the personal utility of SBSs， an algorithm to realize the collaborative computing between SBSs is proposed in combination with the Stackelberg game model with multi?master and multi?slave. The Nash equilibrium solution of non?cooperative game between SBSs is solved by means of the loop iteration. The feasibility and effectiveness of the algorithm are verified by the experiments with Matlab.

Keywords： small base station; edge computing; collaborative computing; Stackelberg game; nash equilibrium; simulation analysis

0? 引? 言

隨著萬物互聯時代[1]的到來，數據呈現出爆炸性的增長，這使得傳統的集中式云計算模型在應用服務實時性、用戶隱私保護和數據傳輸能耗等方面都出現了問題。在此背景下，一種新的在網絡邊緣執行計算的模型，即邊緣計算隨之誕生。

小型基站（SBSs）被認為是邊緣計算中關鍵的支撐設備，具有計算和存儲能力，可以作為云的替代品，為終端用戶提供任務卸載計算。但與云數據中心相比，SBS計算資源是有限的，依賴單個SBS會極大地限制邊緣計算的性能[2]。幸運的是，下一代（5G）移動網絡中SBSs的部署非常密集[3]，這為鄰近的SBSs間實現協同計算提供了可能。

本文中的SBSs是由個人部署的，因此每個SBS無法獲得全局信息。本文結合Stackelberg博弈模型，提出一種以最優化SBSs個人效用函數為目標的SBSs間協同計算算法。在該算法中考慮了SBSs間的通信和計算的過程[4]，將其產生的時延和能耗分別建模并歸一化為運行開銷[5]，同時為了SBS能夠更好地參與到邊緣計算協同當中，引入了激勵機制。針對上述兩種開銷，過載的SBSs對任務進行本地計算或協同計算的選擇[6]。最后通過循環迭代的方法求解非合作博弈的納什均衡。

1? 模型分析與算法實現

1.1? 網絡模型

本文對網絡場景做了如下假設：在一定范圍內密集部署了x個SBSs（[SBSi∈{SBS1，SBS2，…，SBSx}]），由于設備都只具有有限的計算能力，所以本文假設[SBSi]在時隙t最大的卸載任務接收量（下轄終端用戶卸載的任務）為[wmaxi]，同時在時隙t終端用戶向[SBSi]卸載的總任務量為[λi]。根據公式[αi?wmaxi-λi]對[SBSi]在時隙t的情況進行分類。如果[αi<0]，表示[SBSi]有空閑計算資源，可幫助其他有需求的SBSs進行協同計算，本文稱其為資源供應點（后簡稱為供應點），將符合這種情況的SBSs設為集合[SBSS={SBSS1，SBSS2，…，SBSSm}]。如果[αi>0]，表示[SBSi]需要其他SBSs來協助完成計算，本文稱其為資源請求點（簡稱為請求點），將符合的SBSs設為集合[SBSB={SBSB1，SBSB2，…SBSBn}]。每個SBS的狀態是呈現時空變化性的，但本文基于當前時隙t內各個SBS的負載狀態進行分析。由于SBSs間是純分布式的，無集中式管理的，結合文獻[7]中多主多從Stackelberg博弈模型，本文假設“資源供應點”為領導者，“資源請求點”為跟隨者。其中[SBSSj]的出價為[pj]，所有供應點的策略向量定義為[p=（p1，p2，…，pm）]。一個請求點可通過向多個不同的供應點訂購一定量的計算資源，來彌補自身的不足。假定[dij]表示[SBSBi]當前請求[SBSSj]協同處理的任務量，定義[di=（dij，d-ij）]為[SBSBi]向[SBSS]請求的協同計算總任務量，其中[d-ij]表示[SBSBi]向[SBSSj]以外的其他供應點請求協同計算的任務量。[d=（d1，d2，…，dn）]表示網絡中所有[SBSB]的請求協同計算的策略。為了便于計算，假設每個任務的數據為單位大小，所需計算周期為一個CPU周期。同時定義[αSj]為[SBSSj]的剩余可接收任務量，對于[SBSSj]幫助[SBSBi]協同完成的任務量[dij]，則需要滿足[0≤dij≤αSj]，同時對于[SBSSj]上所有請求協同計算的任務量，也需要滿足[i=1ndij≤αSj]。為了能夠更好地反映博弈中一個參與者對選擇策略的滿意程度，本文在上述研究背景下，建立了[SBSBi]和[SBSSj]的效用函數并進行了分析。

1.2? 資源請求點效用函數

對于請求點而言，它們之間構成了非合作博弈關系。同時由于隱私的原因，請求點之間相互獨立且不會互相告知彼此的信息。在此背景下，本文針對請求點中過載任務量的效用函數進行了分析。該效用函數主要由三部分組成：協同計算開銷、本地計算開銷和激勵機制開銷。下面對這三部分進行建模分析。

1.2.1? 協同計算

協同計算過程的開銷主要分為兩部分，一部分是將數據[dij]從[SBSBi]傳輸至[SBSSj]的傳輸時延和傳輸能耗，其公式分別為：

[tB，trij=1rij]? ? ? ? ? ?（1）

[eB，trij=pij1rij]? ? ? ? ? （2）

式中：[rij]為[SBSBi]與[SBSSj]之間的傳輸速率;[pij]為[SBSBi]向[SBSSj]傳輸時的功率。

另一部分是在[SBSSj]上的計算時延，本文根據M/M/1排隊系統對計算時延進行建模，每個任務的平均計算延遲（包括任務等待時間和處理時間）公式如下：

[tS，lij=1fSj-ωSj]? ? ? ? ? （3）

式中，[ωSj]為[SBSSj]上的總任務量，[ωSj=λSj+i=1ndij]，[i=1ndij]為[SBSSj]終端卸載任務量與協同任務量之和。

因此，[SBSBi]請求協同計算時的開銷為：

[CB，tri=i=1n[dijeB，trij+υ（tB，trijdij+tS，lijωSj）]] （4）

式中，[υ]為延遲成本和能量成本的歸一化系數。

1.2.2? 激勵機制

SBSs通常由個人用戶（例如家庭/企業所有者）擁有和部署，因此如果沒有適當的激勵機制，SBSs將不愿意參與邊緣的協同計算過程。結合網絡模型中供應點的出價，可得當[SBSBi]向[SBSSj]請求協同計算的任務量為[dij]時，需要向[SBSSj]支付的價格為[sij=qijpj]。

因此，[SBSBi]向[SBSS]支付的總費用為：

[SBi=j=1mdijpj]? ? ? ? （5）

1.2.3? 本地計算

在時隙t時，可能會出現協同計算成本高于本地計算成本的情況，所以可能部分過載任務會選擇在本地進行計算。針對[SBSBi]本地計算任務時的開銷進行建模。首先利用M/M/1排隊系統對計算時延進行建模，每個任務的平均計算延遲（包括任務等待時間和處理時間）為：

[tB，li=1fBi-ωBi]? ? ? ? ? （6）

式中，[ωBi]表示在[SBSBi]處理的工作負載大小，[ωBi=λBi-j=1mdij]。同時根據文獻[8]可知[SBSBi]處理每個任務的計算能耗與CPU速度的平方成正比，可以表示為：

[eB，li=κ（fBi）2]? ? ? ? ? （7）

式中，[κ]表示常量，取決于CPU架構。

因此，在[SBSBi]上完成任務的計算開銷為：

[CB，li=βBi（eB，li+υtB，li）]? ? ?（8）

式中，[βBi]是過載任務量，[βBi=αBi-j=1mdij]。

1.2.4? 效用函數

根據上述三個模型，本節給出了請求點的效用函數，假定存在請求點[SBSBi]，其效用函數定義為[FBi（p，di，d-i）]，可以表示為：

[FBi（p，di，d-i）=-（CB，tri+CB，li+SBi）] （9）

每個請求點根據當前的價格策略[p]，調整自身策略，最終實現效用函數[FBi]的最優化，即[max{FBi（p*，di，d*-i）}]，其中[p*]和[d*-i]表示博弈中的其他參與者都各自選擇了最優的價格策略和協同計算策略。

1.3? 資源供應點效用函數

本文中的供應點效用函數只考慮了出售計算資源得到的收益，所以供應點效用函數可以利用收益函數[Gj（pj，q）]來表示。定義[SBSSj]的收益函數為[Gj（pj，d）=Qjpj]，其中[Qj=i=1ndij]表示請求點向[SBSSj]請求的協同計算任務總量。因為請求點的選擇會根據供應點價格不同而產生變化，所以提供點的價格并不是越高越好，而是選擇使自身收益最大化的價格策略。假設[SBSSj]的最優價格策略是[p*j]，則其最大收益為[max{Gj（pj，p*-j，d）}]，其中[p*-j]和[d*]表示博弈中其他參與者都選擇了使自身效用最優的價格策略和協同計算策略。

1.4? 資源請求點非合作博弈的納什均衡點

納什均衡是非合作博弈問題的關鍵，同時也是非合作博弈的解。當達到納什均衡后，非合作博弈中的每個參與者的效用函數都達到最大值，且參與者單方面改變自身的策略不會增加自身的收益。本節對納什均衡解的存在性進行了證明。

定理1 職對于供應點價格策略[p=（p1，p2，???，pm）]給定的情況下，請求點之間存在非合作博弈，并存在納什均衡點[d*-i]，使所有請求點的效用函數最優化，即[max{FBi（p*，di，d*-i）}]。

證明? 顯然，任意請求點[SBSBi]的任務協同計算策略[di]是歐幾里得空間中的有界閉集。此外，用戶的效用函數[FBi]在其策略空間上是連續的。對任意請求點[SBSBi]的效用函數求一階偏導得：

[fi（dij）=?FBi（p，di，d-i）?dij? ? ? =-（eB，trij-eB，trij+υtB，trij+pj）+υfSj（fSJ-ωSj）2-? ? ? 1（fBi-ωBi）2-βBi1（fBi-ωBi）2] （10）

對[SBSBi]的效用函數求二階偏導得：[?F2i（p，di，d-i）?d2ij=-2υfSj（fSj-ωSj）3+? ? ? ? ? ? ? ? ? ? ? ? ? ?1（fBi-ωBi）2+βBi（fBi-ωBi）3<0] （11）

式中，[βBi>0，fSj>0，υ>0]，可見請求點的效用函數是凹函數，確保了納什均衡的存在性[9]。

1.5? Stackelberg博弈問題的求解

由于SBS無法獲取全局信息，因此，本文采用了一種循環迭代的方法來求解Stackelberg博弈的納什均衡。假設在t 時供應點的價格策略為p（t），請求點根據當前價格調節協同計算策略，達到納什均衡。其中，協同計算任務量的變化率與請求點效用函數的梯度成正比。

[ddijdτ=dij～=?Fi（p，di，d-i）?dij]? ? ? （12）

式中，[τ]是時間變量。效用函數凹函數的特性保證了迭代算法能夠收斂到博弈的納什均衡點[7]，因此，[SBSBi]協同計算任務量迭代方程可表示為：

[dij（τ+1）=dij（τ）+ξidij～]? ? （13）

式中，[ξi>0]表示請求點卸載任務調節步長。

在請求點之間達到納什均衡后，供應點根據各請求點的任務協同計算策略來調整自己的出價。供應點的價格變化率可通過其邊際效用來表示，因此對任意資源供應點[SBSsj]的價格迭代方程為：

[pj（t+1）=pj（t）+ψj?Gj（p（t），d（t））?pj（t）] （14）

式中，[ψj>0]表示供應點價格策略調節步長。

資源供應點的邊際效用可以通過一個小的變化量[ε]（例如[ε=10-4]）來計算其對效用產生的影響[8]。因此，邊際收益可以粗略的計算為：

[?Gj（p（t），d（t））?pj（t）≈[Gj（…，pj（t）+ε，…）-? ? ? ? ? ? ? ? ? ? ? ? ? ? Gj（…，pj（t）-ε，…）]（2ε）-1] （15）

在請求點達到納什均衡過程中，供應點保持價格不變，觀察并等候請求點的任務協同計算策略達到穩定。這一等候時間即是供應點一次迭代的間隔時間[Δt]，[Δt]也是所有請求點迭代并達到納什均衡的時間間隔。所以供應點根據式（14）和式（15）在多個[Δt]內進行價格迭代。每個[Δt]中多個請求點根據式（12）和式（13）在時間間隔[Δτ]中進行迭代。對整個網絡而言，迭代的最終結果是請求點和供應點得到了各自最優的協同計算策略[d*]和價格策略[p*]，算法的時間序列如圖1所示。在上述的迭代過程分析的基礎上，給出實現協同計算的算法流程圖，如圖2所示。

2? 實驗仿真與分析

本文選擇了Matlab 2014a仿真平臺進行實驗，輔助以Origin 9.0和Office 2010繪圖。

2.1? 參數設定

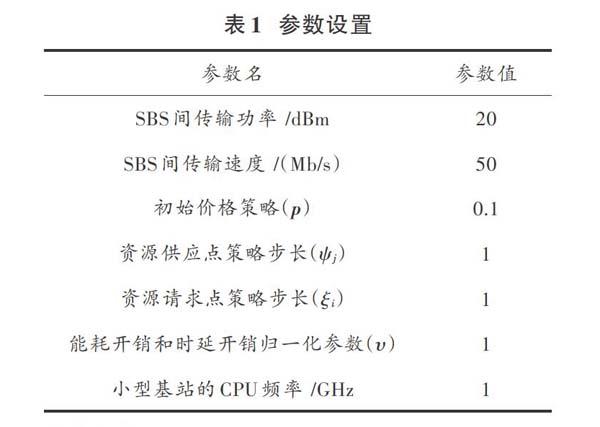
本節對仿真系統的參數進行了設置[9?10]，具體情況如表1所示。假設整個無線網絡環境為100 m×100 m×100 m，仿真環境中部署了10個同構的小型基站，每個小型基站接收到的終端用戶卸載任務到達速率（單位：個/s）為[λi∈（0，300）]。

2.2? 結果分析

本次實驗從資源供應點和資源請求點兩個集合中分別選取一個小型基站進行分析，并將其迭代運行情況進行繪圖，如圖3、圖4所示。首先由圖3可知，在迭代的過程中，資源請求點的效用函數整體呈現增長的趨勢，在趨向收斂的過程中略微有所減小，但達到納什均衡點后，收益最終趨于穩定。隨著本地計算開銷的減少，協同計算開銷和激勵機制的開銷都在增長，但在達到納什均衡之后趨于平穩。這是由于在達到納什均衡后，更改任何策略都無法使效用函數的值更優，因此不再改變任務協同計算策略。圖4中，從曲線上可以看出資源供應點的效用函數是基于價格的凹函數。在價格從0.1逐漸增大的過程中，資源供應點的效用函數隨之先增大后減小，在0.37左右達到最大值。這是由于在競爭的過程中，提高價格可以提升自身的效用函數，但是如果價格過高，就會失去競爭力，資源請求點就會選擇其他的資源提供點來進行協同計算。

3? 結? 語

本文針對邊緣環境中的小型基站間的協同計算進行研究，在同時考慮了請求點和供應點的效用函數最優的情況下，通過Stackelberg博弈分析了兩者的交互關系，提出了一種邊緣協同計算的方法。并通過仿真實驗證明循環迭代的方法可使其達到納什均衡，可以使每個小型基站的效用函數最大化，同時也提供了網絡的資源利用率。本文下一步的工作是對復雜任務的情況進行分析，另外在計算資源供應點效用時還需對其運行開銷進行考慮。

參考文獻

[1] 施巍松，孫輝，曹杰，等.邊緣計算：萬物互聯時代新型計算模型[J].計算機研究與發展，2017，54（5）：907?924.

[2] 周悅芝，張迪.近端云計算：后云計算時代的機遇與挑戰[J].計算機學報，2018，41（25）：1?24.

[3] ANDREWS J G， BUZZI S， CHOI W， et al. What will 5g be？ [J]. IEEE journal on selected areas in communications， 2014， 32（6）： 1065?1082.

[4] ZHANG H Q， XIAO Y， BU S R， et al. Computing resource allocation in three?tier IoT fog networks： a joint optimization approach combining Stackelberg game and matching [J]. IEEE Internet of Things journal， 2017， 4（5）： 1204?1215.

[5] 孟陳融.面向邊緣計算的數據中心服務資源調度機制研究[D].北京：北京郵電大學，2018.

[6] 李波，黃鑫，牛力，等.車載邊緣計算環境中的任務卸載決策和優化[J].微電子學與計算機，2019，36（2）：78?82.

[7] 田厚平，郭亞軍，王學軍.一類基于進化博弈的多主多從Stackelberg對策算法[J].系統工程學報，2005（3）：303?307.

[8] CHEN L X， XU J. Socially trusted collaborative edge computing in ultra dense networks [C]// Proceedings of the Second ACM/IEEE Symposium on Edge Computing. San Jose： ACM， 2017： 9.

[9] 姜永，陳山枝，胡博.異構無線網絡中基于Stackelberg博弈的分布式定價和資源分配算法[J].通信學報，2013，34（1）：61?68.

[10] CHEN L X， ZHOU S， XU J X. Computation peer offloading for energy?constrained mobile edge computing in small?cell networks [J]. IEEE/ACM transactions on networking， 2018， 26（4）： 1619?1632.