含細觀孔隙Al/Al2O3梯度功能材料彈性模量研究

何濟滄 劉齊文 沈 強 劉立勝

（1 武漢理工大學新材料力學理論與應用湖北省重點實驗室，武漢 430070）

（2 武漢理工大學材料復合新技術國家重點實驗室，武漢 430070）

0 引言

預測多相復合材料的有效彈性模量一直是一個經典、重要而富有挑戰性的問題，在所有與力學相關的領域都有應用［1-6］。眾所周知，多相復合材料的有效彈性模量不僅取決于各組分相應的彈性性能和體積分數，還與其細觀結構有關。

Al/Al2O3梯度功能材料是一種先進的多相復合材料，由于其具有密度小、耐高溫、耐磨損、抗熱震等特點，被廣泛的應用于現代航天工業中［7］。Al/Al2O3梯度功能材料中各組分材料的彈性模量相差較大，細觀結構較為復雜，在制造和運輸的過程中還極易產生孔隙，導致其彈性模量的精準預測較為困難，受到了許多專家學者的關注。MOON 等［8］對比了多種預測Al/Al2O3梯度功能材料彈性模量的方法，發現采用適當微觀結構形狀因子的EMA方法計算的結果更加準確。WANG 等［9］在預測Al/Al2O3梯度功能材料彈性模量的時候發現細觀孔隙的影響是不可忽略的。SENTHIL 等［10］利用漸近均勻化方法預測了Al/Al2O3梯度功能材料的彈性模量，預測的彈性模量與自洽方法的結果十分接近。

而對于多孔復合結構等效彈性模量的預測，漸近均勻化方法已經經歷了20 多年的發展。早在1997年，HASSANI 等［11］就已經開始利用漸近均勻化方法對周期性多孔復合結構的力學性能進行了預測。莊守兵等［12］把漸近均勻化理論應用于多孔材料彈性本構的數值模擬，通過對正方形孔洞蜂窩材料有效模量的計算比較，表明漸近均勻化方法可以得到較準確的有效彈性模量。張斌［13］利用漸近均勻化理論測定了松質骨的彈性模量，通過多項式擬合得到了表觀密度與等效彈性模量之間的數值關系。張新等［14］利用漸近均勻化方法預測了多孔混凝土的等效彈性模量，計算結果表明隨機單胞模型能反映細觀的非均質性，三維均勻化理論計算得到的等效彈性模量變化趨勢比較符合試驗結果。

目前對Al/Al2O3梯度功能材料彈性模量的研究僅限于完美的Al/Al2O3梯度功能材料，而對于Al/Al2O3梯度功能材料中真實存在的細觀孔隙，研究還相對較少。本文利用漸近均勻化方法在研究多孔復合結構等效力學性能方面的優勢，對含細觀孔隙Al/Al2O3梯度功能材料的彈性模量進行研究，分析細觀孔隙的個數、大小、位置和孔隙率對材料彈性模量的影響。最后在忽略孔隙個數等次要因素的情況下，擬合與孔隙率和Al2O3體積分數相關的含細觀孔隙Al/Al2O3梯度功能材料彈性模量的預測公式。

1 漸進均勻化方法

漸近均勻化方法是利用漸近展開和周期性假設來代替具有快速振蕩系數微分方程的一種極限理論。這種方法不僅能計算非均質材料的宏觀物理性能，還能對結構進行多尺度分析。目前已經有很多研究將漸近均勻化方法運用到各種不同材料和結構的等效宏觀性能預測中。

隨著漸近均勻化理論的發展，在漸近均勻化方法中引入了一種更接近于實際情況的局部周期性假設，即假定非均質材料僅在局部區域滿足周期性假設，這一假設的引入擴大了漸近均勻化方法的使用范圍，使其能解決如梯度功能材料等更為復雜的復合材料等效模量計算［15］。

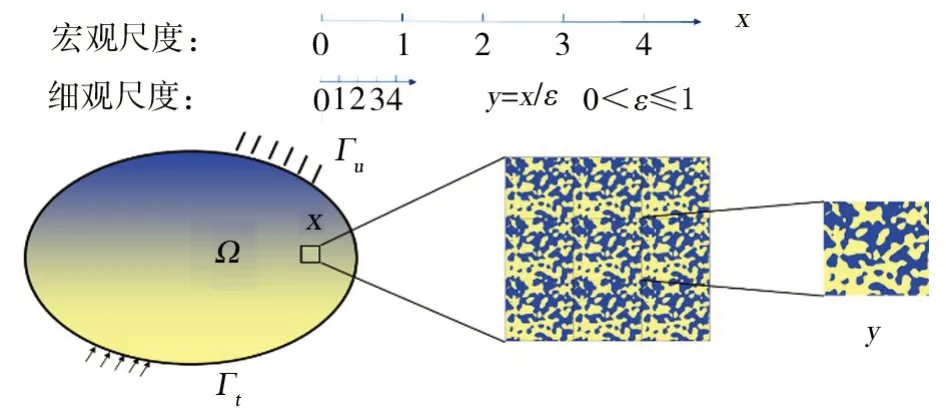
圖1 功能梯度結構多尺度模型示意圖Fig.1 Schematic diagram of multi-scale model of functional gradient structure

圖1為一個功能梯度結構，在宏觀位置x處周圍非常小的范圍內可認為是由單胞反復堆積形成的周期性結構。單胞的尺度y相對于宏觀的幾何尺寸為小量。對于非均勻的材料來說，宏觀結構在外部作用下位移和應力等結構場變量將隨宏觀位置的改變而改變。同時由于細觀上的復雜結構，使得這些結構場變量在宏觀位置x處非常小的鄰域內也會有很大的變化。因此所有的變量都依賴于宏觀和細觀兩種尺度，即:

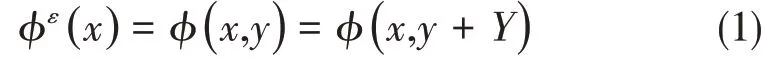
式中，單胞的周期為Y，y為細觀坐標，x為宏觀坐標，y=x/ε。

虛功原理表示的線彈性控制微分方程為:

將位移進行漸近展開:

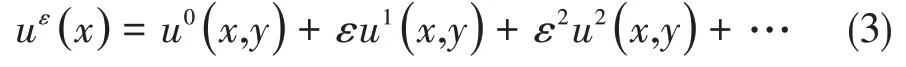
將位移的漸進展開式代入虛功原理表示的線彈性控制方程中得:

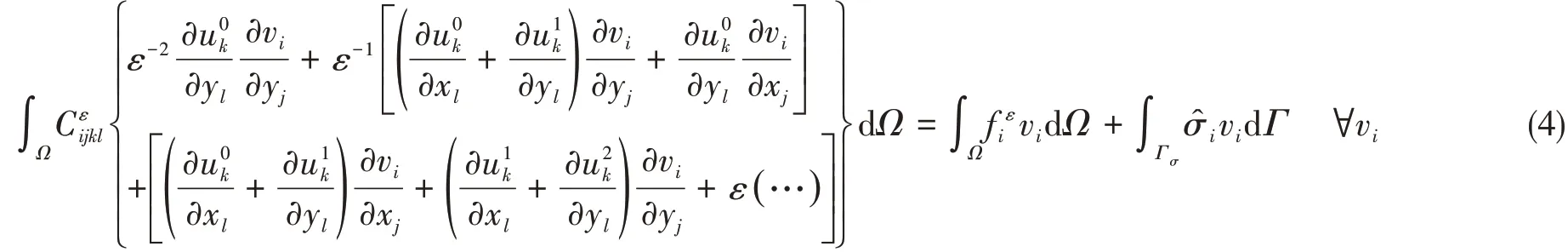
對于任意的ε，（4）式均成立，所以位移場漸近展開的第一項僅依賴于宏觀坐標x，即u0k(x，y)=u0k(x)。

在u0(x)已知的情況下，則u1(x，y)可以用u0(x)表示［16］，即:

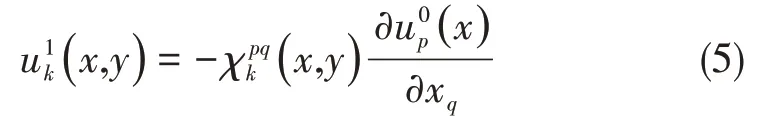
將式（4）與ε相乘，并取ε→0+和vi=vi(y)，再將（5）帶入得:

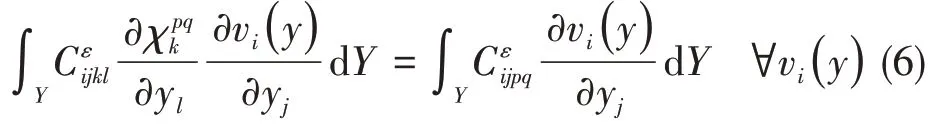
在確定的χpqk下，均勻化的彈性矩陣被求得:

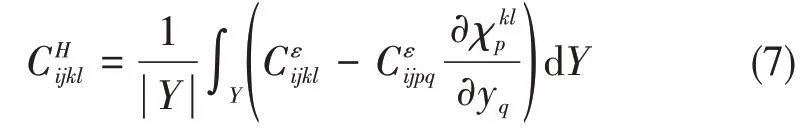
將細觀單胞用有限元方法進行離散得到均勻化問題的有限元形式為:

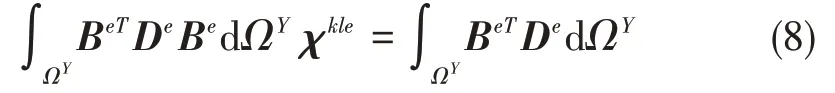
式中，e是單胞ΩY區域內離散后的單元，De是單元彈性矩陣，Be是單元應變矩陣，χkle是相應單元的節點位移。

單胞離散后，可以采用有限元形式對單元宏觀結構的彈性性能進行表述:

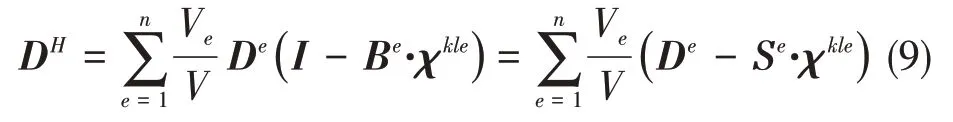
式中，DH是均勻化方法計算所得到的宏觀有效彈性矩陣，n是單胞單元總數，Ve是單元的體積，De是單元彈性矩陣，V是單胞結構的總體積，I是單位矩陣，Se是單元應力矩陣。

2 細觀模型

對于Al/Al2O3梯度功能材料細觀模型的構建，采用二維高斯函數在單胞區域內隨機疊加的方法，構成細觀形貌函數:

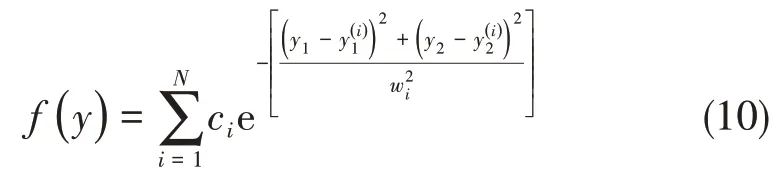
式中，N代表二維高斯函數的疊加次數，高斯函數中的ci∈[ - 1，1]和都為隨機數，wi是一個取決于N的空間寬度:

式中，l為單胞寬度。

通過在隨機形貌函數上確定截面值，當f(y)≥的時候為相，當f(y)＜的時候為相，生成隨機分布的兩相非均質材料單胞。圖2（a）是N為800，相體積分數為40%的單胞，圖2（b）為真實Al/Al2O3梯度功能材料細觀形貌。后文中所采用的單胞尺寸均為30μm。

圖2 單胞形貌Fig.2 Single cell morphology

實際的Al/Al2O3梯度功能材料中，孔隙的形狀各式各樣，孔隙大小和位置均為隨機分布，為了對孔隙的影響進行定量分析，假設Al/Al2O3梯度功能材料各細觀組分都是理想均勻、各向同性的彈性材料，采用不同半徑的圓孔模擬材料中的孔隙。由于材料的細觀結構和隨機孔隙的位置、大小均不確定，為體現結果的一般性，所有的結果都為生成10 次隨機細觀結構計算得到的平均值。圖3為孔隙率為10%，Al2O3體積分數為40%的含9 個隨機孔隙的Al/Al2O3梯度功能材料單胞網格模型。

圖3 單胞網格模型Fig.3 Single cell grid model

3 結果與討論

3.1 實驗對比

為了驗證漸近均勻化方法計算Al/Al2O3梯度功能材料彈性模量的有效性和準確性，將漸近均勻化方法計算未含細觀孔隙的Al/Al2O3功能梯度結構得到的彈性模量和文獻［8］中實驗得到的彈性模量進行對比。均勻化過程中需要的Al 和Al2O3材料彈性參數如表1所示。均勻化計算得到的結果如表2所示，漸近均勻化方法求得的等效模量與實驗結果趨勢相同，說明漸近均勻化方法預測Al/Al2O3梯度功能材料的等效彈性模量是可行的。當Al2O3體積分數接近100%的時候均勻化計算結果與實驗相對誤差較小，僅為0.25%，而當Al2O3體積分數逐漸減小，Al 和Al2O3在細觀上形成交互結構的時候，漸近均勻化結果相對于實驗的結果誤差增大，最大達到了10.16%。這一結果可以歸結于兩個方面的影響:（1）當Al 和Al2O3在細觀上形成交互結構的時候，細觀結構變得復雜，而每個樣品的細觀結構又都是不確定的，這將增大梯度功能材料等效彈性模量的預測難度；（2）Al/Al2O3梯度功能材料中有許多的細觀孔隙，在預測梯度功能材料力學性質的時候，忽略孔隙的存在將會使預測的彈性模量大于實際的彈性模量。

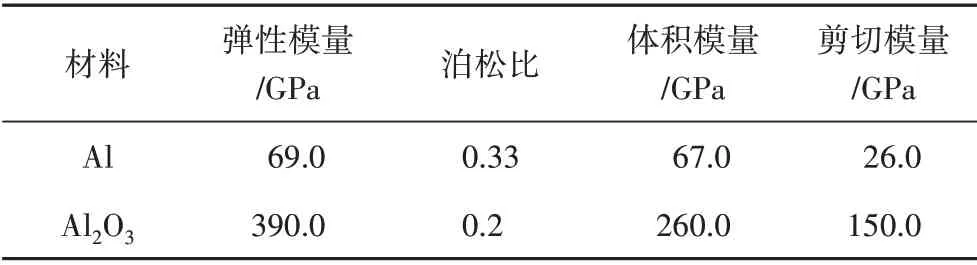
表1 材料參數［8］Tab.1 Material parameters

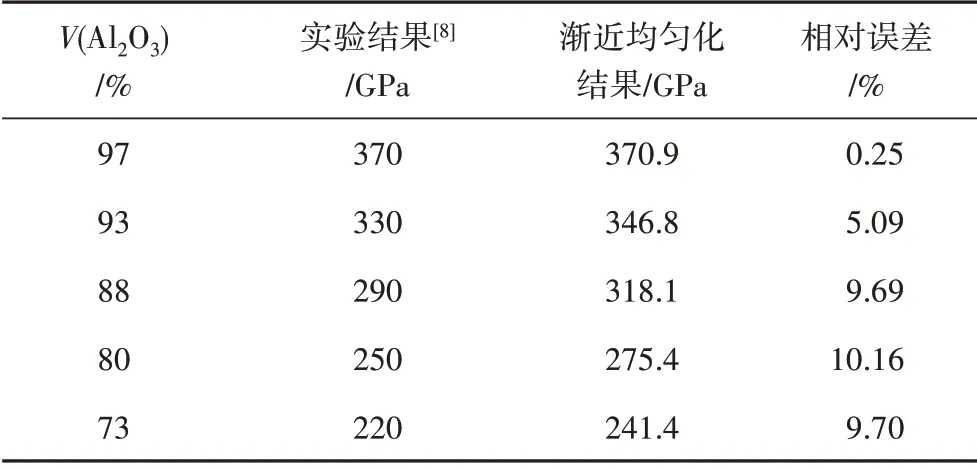
表2 Al/Al2O3梯度功能材料均勻化等效模量和實驗對比Tab.2 Comparison of homogenization equivalent modulus and experiment of Al/Al2O3 FGM

3.2 細觀孔隙對Al/Al2O3梯度功能材料彈性模量的影響

在細觀層面上，Al/Al2O3梯度功能材料中的孔隙各式各樣，為了研究可能的影響因素，利用漸近均勻化方法分別分析了孔隙的個數、位置、大小和孔隙率對含細觀孔隙Al/Al2O3梯度功能材料彈性模量的影響。

3.2.1 孔隙數量的影響

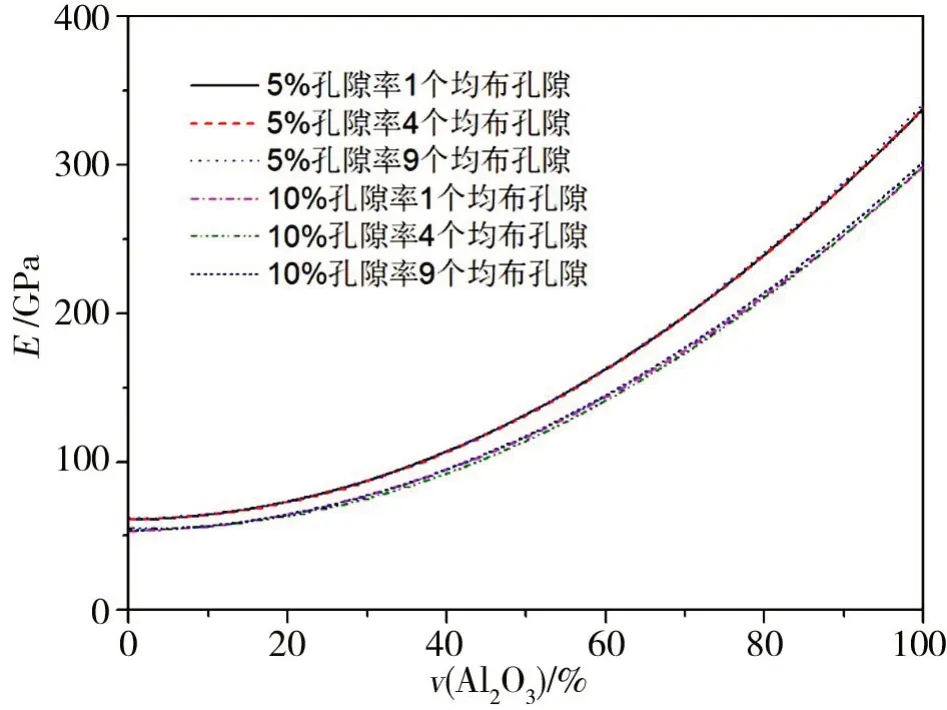
圖4 孔隙個數對Al/Al2O3梯度功能材料均勻化等效模量的影響Fig.4 Influence of the number of pores on the homogenization equivalent modulus of Al/Al2O3 FGM

圖4為孔隙個數對Al/Al2O3梯度功能材料均勻化等效模量的影響。結果表明，在孔隙率和孔隙形狀都不變的情況下，孔隙的個數對Al/Al2O3梯度功能材料彈性模量的影響非常小，在任何體積分數下，Al/Al2O3梯度功能材料的彈性模量變化均不超過1%。

3.2.2 孔隙位置和大小的影響

圖5展示了5%和10%孔隙率下孔隙位置和大小對Al/Al2O3梯度功能材料彈性模量的影響。

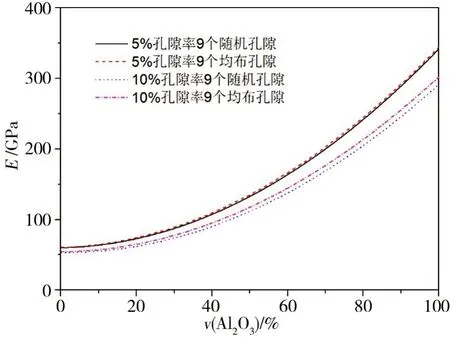
圖5 孔隙位置和大小對Al/Al2O3梯度功能材料彈性模量的影響Fig.5 Influence of pore location and size on the homogenization equivalent modulus of Al/Al2O3 FGM

通過比較含9 個隨機孔隙單胞與含9 個均勻孔隙單胞在不同體積分數下彈性模量發現:在任何體積分數下，彈性模量含均布孔隙單胞的均高于隨機孔隙單胞的。在孔隙率為10%時，彈性模量含均布孔隙單胞的與隨機孔隙單胞的差別更大。在孔隙率為10%、Al2O3體積分數100%時，彈性模量含均布孔隙單胞的比隨機孔隙單胞的大10.5 GPa。而在孔隙率為5%時，相同體積分數下彈性模量含均布孔隙單胞的僅比隨機孔隙單胞的大3.2 GPa。

3.2.3 孔隙率的影響

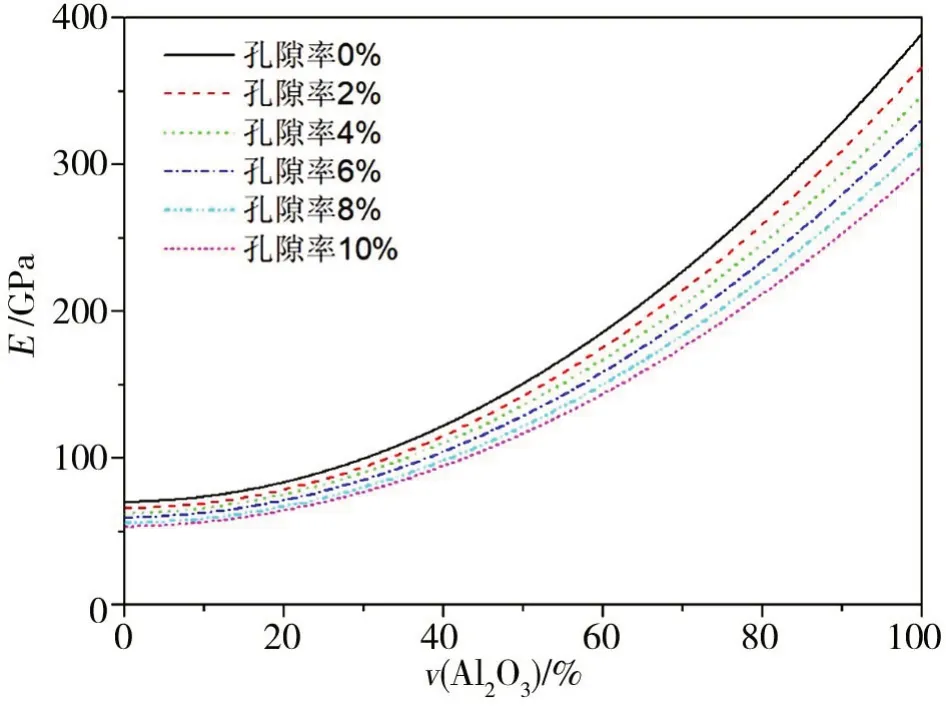
圖6 Al/Al2O3梯度功能材料不同孔隙率下均勻化等效模量Fig.6 Homogenization equivalent modulus of Al/Al2O3 FGM with different porosity

在考慮孔隙數量、大小和位置等影響因素的基礎上，在不同孔隙率和Al2O3體積分數的單胞內分別生成9 個隨機的圓形孔隙，并計算其彈性模量。圖6為不同孔隙率下Al/Al2O3梯度功能材料的均勻化等效彈性模量。

由圖6可知，隨著孔隙率的增大，含細觀孔隙Al/Al2O3梯度功能材料的彈性模量逐漸下降。隨著Al2O3體積分數的增加，Al/Al2O3梯度功能材料彈性模量下降的幅度越來越大。如Al2O3體積分數為0 時，孔隙率為10.0%的Al/Al2O3梯度功能材料相對于孔隙率為0 的僅下降了15.97 GPa，而在Al2O3體積分數為100%時，孔隙率為10.0%的Al/Al2O3梯度功能材料相對于孔隙率為0的下降了90.78 GPa。

3.3 Al/Al2O3梯度功能材料彈性模量預測公式

由于孔隙的數量對Al/Al2O3梯度功能材料彈性模量的影響很小，而實際的Al/Al2O3梯度功能材料內部的孔隙都是隨機分布的，利用不同孔隙率和體積分數下含9 個隨機孔隙單胞的等效彈性模量擬合出了一個關于孔隙率和Al2O3體積分數的彈性模量預測公式。圖7為彈性模量與孔隙率和Al2O3體積分數關系的示意圖。

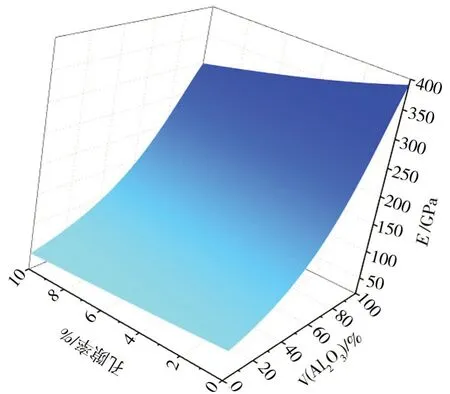
圖7 彈性模量與孔隙率和Al2O3體積分數關系的示意圖Fig.7 Schematic diagram of relationship between elastic modulus and porosity and Al2O3 volume fraction

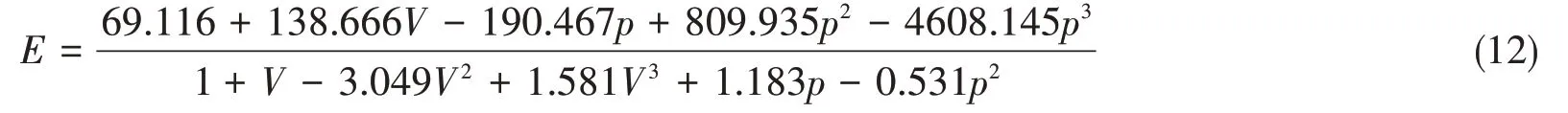
式中，V為Al2O3的體積分數，p為孔隙率，E為彈性模量。公式（12）僅在孔隙率小于10%的情況下有效。

4 結論

基于漸近均勻化方法對含細觀孔隙Al/Al2O3梯度功能材料的彈性模量進行了研究，在忽略孔隙個數等次要因素的情況下，擬合得到了與孔隙率和Al2O3體積分數相關的含細觀孔隙的Al/Al2O3梯度功能材料彈性模量的預測公式。并通過分析孔隙個數、大小、位置和孔隙率對梯度功能材料彈性模量的影響得到了以下結論:

（1）預測Al/Al2O3梯度功能材料的彈性模量時，忽略孔隙的影響將會導致預測的彈性模量值偏大；

（2）在相同孔隙率下，孔隙個數對Al/Al2O3梯度功能材料的彈性模量影響不大，孔隙的大小和位置對Al/Al2O3梯度功能材料的彈性模量有著明顯的影響，在各個體積分數下，彈性模量含隨機分布孔隙的單胞均小于均勻分布孔隙的單胞；

（3）隨著孔隙率的增加，Al/Al2O3梯度功能材料的彈性模量在任何體積分數下均減小，且下降幅度隨著Al2O3體積分數的增加而變大。