基于響應曲面法的高速內冷銑削AISI304不銹鋼銑削力

薛 姣 李廣慧 尹凝霞 沈 燦 譚光宇

（廣東海洋大學機械與動力工程學院，湛江 524088）

文 摘 針對硬質合金刀具高速內冷銑削AISI304不銹鋼時，切削力大、切削溫度高及加工表面質量低的問題。基于響應曲面中心復合設計方法進行高速內冷銑削實驗，建立了銑削力分量二階回歸預測模型，并進行了實驗驗證。對比了干式與內冷銑削后的加工表面質量，分析了銑削參數對銑削力分量的影響規律，以銑削力分量最小為目標優化了銑削參數。結果表明：進給力和徑向力的預測值與實驗值的誤差分別為4.77%和6.16%；內冷銑削的Ra 為0.193～0.327μm；對銑削力分量的影響是銑削深度＞轉速＞進給量，隨著銑削深度和轉速的增加，進給力先升高后降低，徑向力逐步增加，銑削深度與轉速的交互作用對進給力和徑向力的影響顯著；轉速11 643.63 r/min、銑削深度1 mm、進給量0.08 mm/r為最優銑削參數組合。

0 引言

AISI304 不銹鋼因在高溫腐蝕的環境下依然具有優良的綜合性能而廣泛應用于航空、船舶、醫療等高技術領域，是一種常用的宇航材料，如飛機發動機冷端葉片［1］。但其熱導率低、塑性強使它在切削加工過程中具有切削力大、表面質量難以控制以及加工硬化嚴重的特點，導致刀具磨損加劇、粘屑、耐用度降低［2-3］。

高速銑削是一個復雜的非線性銑削加工過程，加工表面的質量和切削力都與切削過程中的冷卻方式緊密相關。張春燕等［4］對鈦合金進行了內冷式MQL 銑削實驗，分析了銑削參數對已加工表面質量的影響。邵軍杰等［5］對1Cr18Ni9Ti 奧氏體不銹鋼進行了平面銑削實驗，建立了表面粗糙度和銑削力模型。孫燕華等［6］通過正交實驗和多元線性回歸建立了0Cr18Ni9銑削力模型。但是對0Cr18Ni9銑削力及刀具的研究主要是干式或外冷的銑削環境，內冷式微量潤滑設備昂貴且操作復雜。內冷銑削是指切削液經過刀具內部螺旋孔，從刀具低刃端直接噴到切削區域對刀具及切削區域進行冷卻潤滑。切削液能夠有效達到切削區，并在刀具與切屑間形成潤滑膜，大大降低了刀屑之間的摩擦，減少了刀具磨損，提高了表面加工質量。因而研究高速內冷銑削過程中銑削力的變化規律，影響銑削力的主要銑削因素，建立可靠的銑削力模型對減少刀具的磨損、保證加工完整性等具有重要意義［7-9］。

本文重點對高速內冷銑削力進行研究，通過響應曲面中心復合實驗與單因素實驗，建立銑削力分量預測模型，分析銑削參數對銑削力的影響規律，以銑削力分量最小為目標得出最優銑削參數組合，擬為工程實踐提供參考。

1 高速銑削實驗

1.1 設備

采用VMC1000P 主軸出水立式加工中心（主軸最高轉速15 000 r/min，機床額定功率11 kW），Kistler9119AA1 切削力測量系統（測量范圍0～4 kN，靈敏度進給力Fx≈-26 Pc/N，徑向力Fy≈-13 Pc/N），采樣頻率13～26 kHz；Mar Surf PS1 粗糙度測量儀，BT40 刀柄，動平衡等級G2.5/2000 RPM，實驗測力原理示意圖如圖1所示。

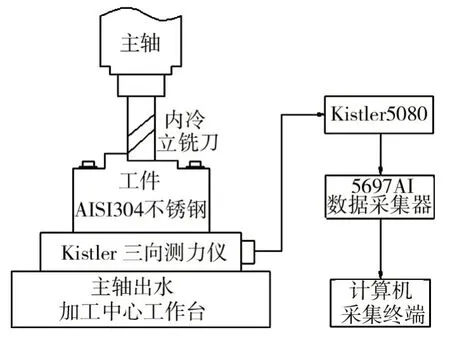
圖1 測力原理示意圖Fig.1 Schematic diagram of force measurement

1.2 實驗條件與方案

采用GU20整體硬質合金4刃雙螺旋內冷孔立銑刀，直徑10 mm，前角5°，后角15°，螺旋角30°，內冷孔直徑1.4 mm，內冷壓力0.3 MPa（表壓）。測試材料是AISI304不銹鋼［10］，尺寸為64 mm×40 mm×80 mm，DX-2型切削液，采用高速內冷銑削，銑削方式為平面順銑。中心復合設計（CCD）方法具有能評估高階多項式預測模型、實驗循環次數少、建模便捷以及預測結果貼近真實值等優勢而在工程中廣泛應用［11］。

根據機械加工工藝手冊、工件及銑刀材料選擇實驗銑削參數，實驗設計如表1所示。

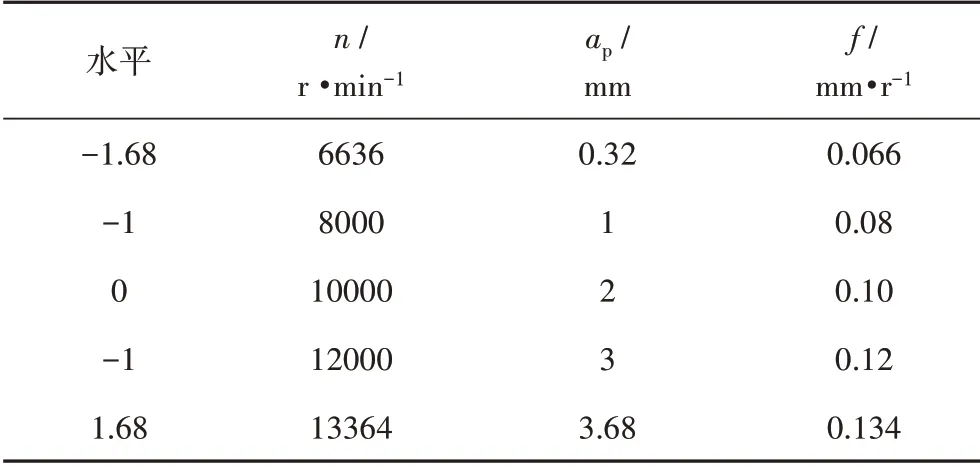
表1 實驗因素與水平Tab.1 Experimental factors and levels

2 結果分析與討論

2.1 實驗結果

通過銑削實驗獲得三個方向銑削力，其中軸向力Fz在銑削過程中波動較小且關于零軸對稱分布，故本文只分析Fx和Fy，銑削力取切削穩定區連續30個峰值的平均值，1～20 組為中心復合實驗，21～26 組為補充實驗，實驗結果如表2所示。

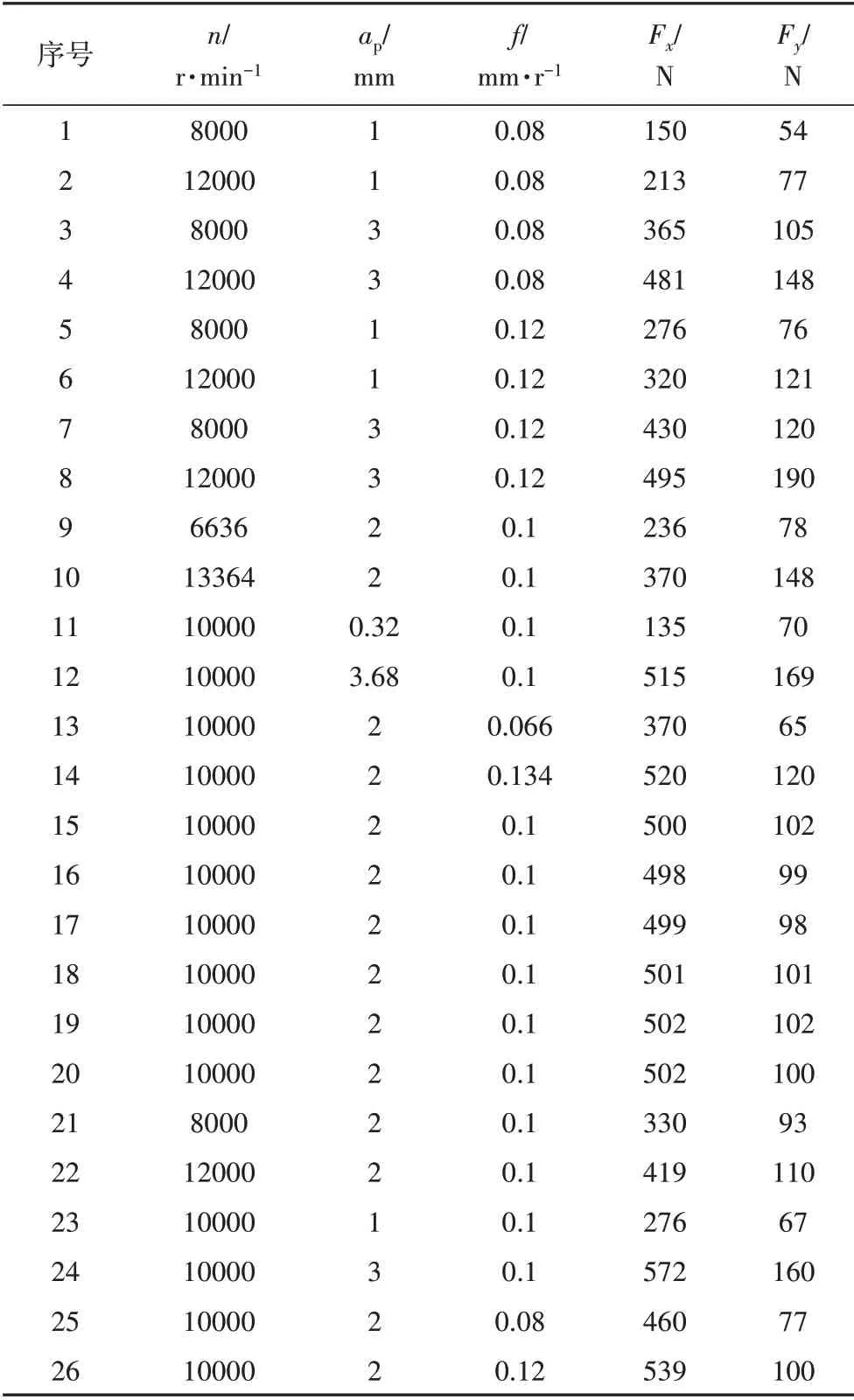
表2 實驗結果Tab.2 The experimental results

2.2 內冷銑削力模型的建立與方差分析

響應曲面法能夠反映響應值與響應因子之間的關系，克服了正交實驗不能給出直觀圖的缺陷。假設影響因素顯著性水平P＜0.05，采用響應曲面中心復合法對銑削力分量與銑削參數之間的關系進行分析，根據實驗數據運用最小二乘法擬合二階回歸方程模型，并對其進行方差分析以判別模型擬合的優良程度，二階數學模型如下［12］:

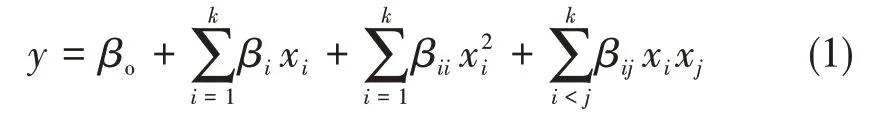
式中，y為響應值，x為銑削因子變量，βo、βi、βii、βij分別為各項系數。

通過形式轉換，把實驗因素的自由變量和銑削力分量值轉換成矩陣形式，再運用最小二乘法得到上式中的系數值，最后經過銑削參數轉換，建立銑削力分量與銑削因子間的多元回歸預測模型，即:

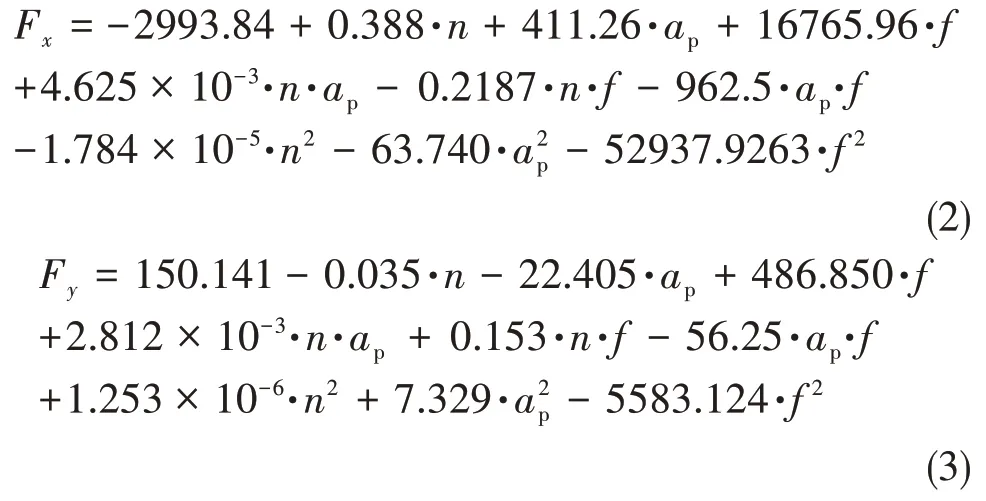
建立二階回歸模型后，進行方差分析，結果見表3［13］。

表3 回歸模型方差分析表Tab.3 ANOVA table for the regression model

由表3可知，Fx方差分析模型中P＜0.000 1，模型非常顯著，多元相關系數R2=0.997 1，校正后的多元相關系數Radj2=0.994 6，表明二階模型擬合結果較好。Fy方差分析模型中P＜0.000 1，模型非常顯著，多元相關系數R2=0.947 6，校正后的多元相關系數Radj2=0.940 4，對實驗結果的擬合程度高。

2.3 銑削力分量模型的驗證及單因素對銑削力分量的影響分析

通過三組單因素實驗進行驗證模型的準確性，并分析了單因素對銑削力分量的影響，具體結果如圖2所示。從圖2中看出，不管是Fx還是Fy，內冷實驗值與預測值在不同轉速、不同銑削深度、不同進給量下變化趨勢均一致，Fx的內冷實驗值與預測值的誤差是4.77%，Fy的內冷實驗值與預測值的誤差是6.16%，表明銑削力分量預測模型的可靠性高。

圖2 單因素對銑削力分量的影響Fig.2 Effect of single factor on milling component force

Fx內冷實驗值高于干式實驗值，是因為在切削液的作用下，切削溫度下降，減小了加工表面的熱軟化，使得銑削力增大［14］；其次，切削液經內冷孔噴出，在離心力的作用下沖擊待加工表面，增大了銑削力。Fy的內冷實驗值略低于干式實驗值，不同的銑削環境對Fy的影響不明顯。對加工后的表面進行測量，內冷銑削后的工件Ra為0.193～0.327μm，干式銑削后的工件Ra為0.330～0.488μm，內冷銑削的表面質量優勢顯著。在圖2中，當轉速在6 636～10 000 r/min時，Fx增加，在10 000～13 364 r/min時，Fx減小，最大值為500 N。這是高速切削的特征之一［15-16］，當工件材料被切削的速度超過了其本身滑移變形的速度時，材料還沒有來得及完成滑移變形就被切掉了；第二切削速度的增加使得被切材料脆性化，銑削力減小。銑削深度在1～3 mm時，Fx增加，在3～4 mm時，Fx減小，最大值為572 N；隨著進給量的增加，Fx緩慢增加。

Fy隨著轉速和進給量的增加增速較小，隨著銑削深度的增加，先增加后平緩減小。

2.4 交互因素對銑削力分量的影響

根據二階回歸方程模型做出銑削參數間交互作用的三維立體響應曲面，結果如圖3和圖4所示。

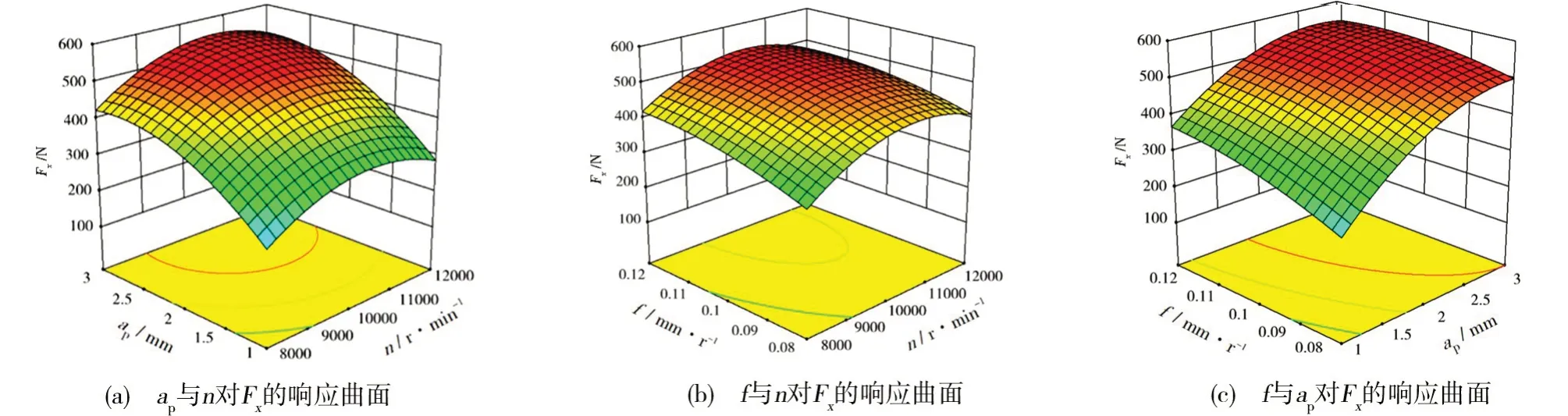
圖3 Fx的響應曲面圖Fig.3 Response surface diagram of Fx

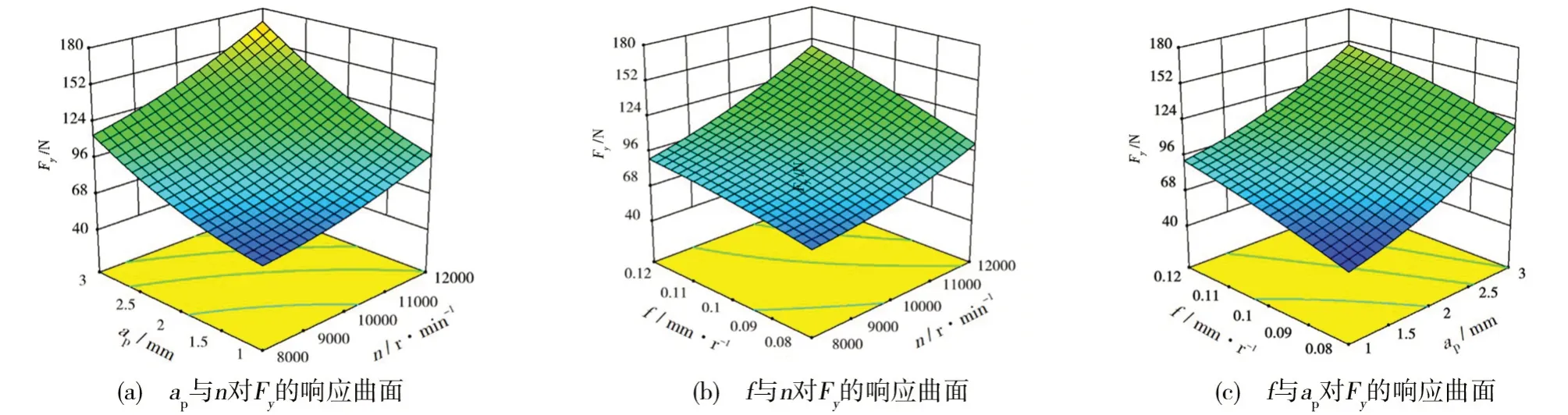
圖4 Fy的響應曲面圖Fig.4 Response surface diagram of Fy

在圖3（a）中的曲面彎曲幅度和目標值范圍明顯大于圖3（b）和圖3（c），可知銑削深度與轉速之間的交互作用對Fx的影響大于銑削深度與進給量的交互用及進給量與轉速的交互作用。從圖3（a）和圖3（b）中得知在銑削深度和進給量不變的情況下，Fx隨著轉速的增加先增大后減小，其原因與上述高速機理相似。由圖3（a）和圖3（c）中得知在轉速和進給量不變的情況下，Fx隨著銑削深度的增大先增加后緩慢減小；由圖3（b）和圖3（c）中得知在銑削深度和轉速不變的情況下，Fx隨著進給量的增加緩慢增加至趨于穩定。

從圖4（a）和圖4（b）中得知在銑削深度和進給量不變的情況下，Fy隨著轉速的增加穩步增大；由圖4（a）和圖4（c）中得知在轉速和進給量不變的情況下，Fy隨著銑削深度的增大而線性增長；由圖4（b）和圖4（c）中得知在銑削深度和轉速不變的情況下，Fy隨著進給量的增加緩慢增加至趨于穩定。

2.5 銑削參數優化

根據上述高速內冷銑削單因素實驗及銑削參數的交互作用對銑削力分量的影響變化分析可知，對銑削力分量的影響是銑削深度＞轉速＞進給量，因此應選擇低的銑削深度、高轉速和小進給量來獲得最小銑削力分量。以此為基礎，在所選的銑削參數范圍內，結合二階響應模型采用最小二乘法求解，得到轉速11 643.63 r/min、銑削深度1 mm、進給量0.08 mm/r，此為銑削力分量最小的銑削參數組合。

3 結論

（1）建立高速內冷銑削的銑削力分量預測模型，并通過方差分析和實驗驗證了預測模型的可靠性高。Fx和Fy的預測值與實驗值的誤差分別為4.77%和6.16%。

（2）對銑削力分量的影響是銑削深度＞轉速＞進給量。Fx隨著銑削深度和轉速的增加先增加后減小，轉速在10 000 r/min 時達到最大值500 N，銑削深度為3 mm 時達到最大值572 N，隨著進給量的增加，Fx緩慢增加，直至趨于穩定；Fy隨著銑削深度、轉速和進給量的增加慢慢升高。銑削深度與轉速同時增加Fx先增加后逐漸減小，Fy持續增加。

（3）Fx內冷銑削高于干式銑削，二者的Fy相差不大，內冷銑削加工質量高，工件Ra為0.193～0.327μm；以銑削力分量最小為優化目標，獲得一組最優銑削參數:轉速11 643.63 r/min，銑削深度1 mm，進給量0.08 mm/r。