90°彎管內流動特性數值研究

秦明坤,李 強，王建普

（1.菏澤泰諾環境科技有限公司，274000；2.菏澤市生態環境局定陶區分局：山東 菏澤 274100）

彎曲管道作為基本的流體運輸管道組成部分，在汽車及航空發動機連接管道、氣力輸送、燃煤及核動力設備管道等方面有著廣泛的應用[1-2]。受管道內輸送介質和彎管內部二次流的影響，管內熱邊界層和流動邊界層會發生不能程度的變化，這些變化會顯著影響管道彎頭部分的傳熱性能，進而影響到管道彎頭的局部應力，給整個設備的安全穩定運行帶來極大的風險，因此，彎曲管道的內部流動狀況成為基礎科學領域的重要研究內容[3-4]。

早期的彎管內的流動狀況研究以實驗為主，采用激光多譜勒測速儀對管內不同雷諾數下的湍流和層流狀態進行分析，探究彎管各位置的壁面壓力和時均速度分布[5-7]。隨著計算機技術的發展，數值模擬逐漸成為更為科學便捷的研究方式。相比實驗研究，數值模擬可以得到大量工程測試無法獲得的數據結果，加快了彎管內流動狀況研究的速度。目前，標準k-epsilion 湍流模型、RNG k-epsilion 湍流模型和大渦模擬是在彎管流動計算中應用應用較多的數值模型，而已有的實驗和數值模擬結果表明，利用標準k-epsilon模型計算結果與實驗符合較好[2-4]。

基于以往研究的基礎，本研究采用fluent 軟件，標準k-epsilon湍流模型，SIMPLE算法，六面體網格，建立90°大曲率彎管內部流場中Navier-Stokes方程，研究了Re數（Re=ρuD/μ，ρ為流體密度，u為入口速度，D為彎管水力直徑，μ為流體動力黏度）、管彎曲度對壓力損失和二次流的影響，分析流場中出現的物理現象和規律。

1 模型的建立

1.1 幾何模型及網格劃分

水平放置的90°圓形彎管各段的幾何尺寸、坐標系定義及網格劃分情況見圖1和圖2。

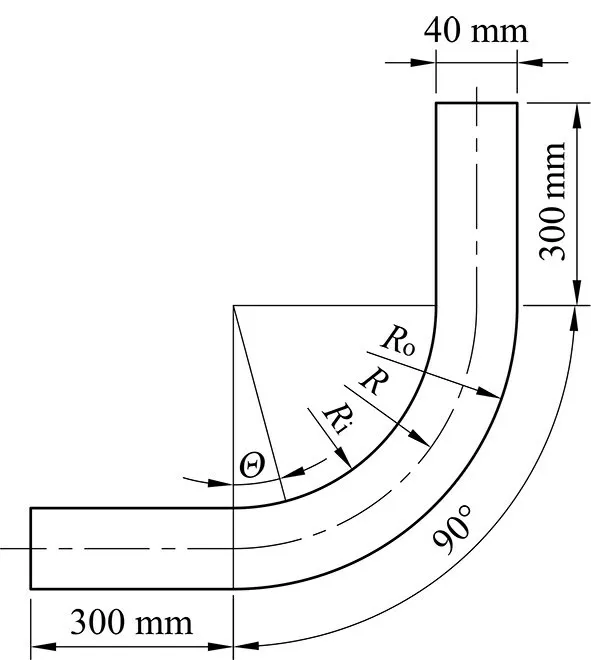
圖1 彎管的幾何尺寸Fig 1 Physical dimension of angle pipe

圖2 彎管結構和網格劃分Fig 2 angle pipe structure and its mesh generation

彎管的彎曲度定義為R/D，其中R為彎曲段平均半徑（R=Ri+Ro，Ri和Ro分別為彎曲段內外徑）。在彎曲段，沿主流方向的坐標定義為圓心角Θ。采用六面體網格劃分方法，入口直管段網格逐漸加密，遞增因子1.03；彎管段流動復雜，網格較密；由彎管至出口處網格由密到疏，遞增因子0.99；壁面設置10 層邊界層，第1 層厚度0.2 mm，遞增因子1.2。

1.2 數學模型及操作參數

管內流體的流動為三維、定常，不可壓縮流動，介質為常溫下（298 K）的水，不考慮換熱和介質所受重力作用，物性參數見表1。

表1 介質參數及邊界條件Tab 1 Parameters of medium and its boundary conditions

流動過程的通用微分方程式為：

[?(ρφ)/?t]+div(ρ ?u φ)=div(Γ grad φ)+S。 (1)

式中，Г為擴散系數，S 為源項，?u 為流體速度矢量，t為非穩態時間；對于特定意義的φ，Г和S具有特定的量。

對于定常流，連續方程為：

將式（1）寫成時均形式后，雷諾應力項的存在造成了雷諾時均方程的不封閉，需要引進相應的湍流模型來實現方程組的封閉。由于Launder等提出的k-epsilon雙方程模型具有較高的計算精度且計算量較小，故選用標準k-epsilon模型來進行雷諾應力項的封閉，近壁面選用Enhanced Wall Treatment進行修正。

采用分離求解器進行求解，壓力-速度耦合方式為SIMPLE，為保證求解物理意義上的準確性和結果的精確性，對流項采用二階迎風差分格式。

2 結果及討論

2.1 管彎曲度對壓力損失的影響

管路壓力損失是衡量管路特性的重要指標。在一般的工業應用中，測算等管徑彎管損失時，常假定管道中速度不變，而通過測量彎管出口后2D或4D處的壁面平均壓力來確定管路損失，如果依靠這種方法來確定損失會得出壓力損失為負的錯誤結論。準確確定管路損失的方法應該將壓力和速度都考慮在內，即采用不同斷面上的總壓差來確定管路損失[3]。采用總壓阻力系數CP對彎管流動的壓力損失進行分析，定義式為(3)，阻力系數越小，經濟性越好。

式中，p 和ps分別為入口和出口總壓，uo為來流速度。

管內流動的阻力損失由2部分組成，分別是沿程阻力損失和局部阻力損失。沿程阻力損失由壁面無滑移粘性阻力造成，局部阻力損失由彎管、變徑、閥門等局部構件引起的流體湍流混合造成。保持Re=50×103，入口段和出口段長度不變，R/D對壓力損失的影響見表2。

表2 R/D對壓力損失的影響Tab 2 Effect of R/D value to pressure loss

由表2 可知，R/D 增加，使得沿程阻力損失增大，然而，流動方向變化變緩，局部阻力損失減小。由圖2知，R/D=1時，管彎曲程度較高，內部流體運動方向發生急劇變化，局部阻力損失占主導地位，沿程阻力損失的減小不明顯，因此阻力系數較高。隨著R/D 的增大，局部阻力損失減小，沿程阻力損失增大，總的阻力損失在R/D≈2.5時最小。

2.2 Re對壓力損失的影響

保持R/D=1.5，研究壓力損失隨Re數的變化情況，結果見圖3。

圖3 Re對壓力損失的影響Fig 3 Effect of Re value to pressure loss

由圖3 可知，隨著Re 數的增大，壓力降成二次曲線性增加，這與壓力損失的理論計算公式相符。阻力系數CP在低Re 數時，達到7.70，當流動處于湍流范圍時（Re≥2 300），CP降至2 以下，更高Re 下的阻力系數在0.4～0.7，這也與已有研究相符[3]。

2.3 管彎曲度對內外壁靜壓分布的影響

保持Re=50×103，研究管彎曲度對內外側靜壓分布的影響，結果如圖4所示。

圖4 管彎曲度對內外壁靜壓分布的影響Fig 4 Effect of the pipe blend degree to static pressure contribution of inside and outside wall

由圖4 可知，R/D=1.0 彎管曲率較大，流動方向急劇變化，內外側靜壓差在Θ=0°時約為0.8 kPa，在Θ=45°時大至1.6 kPa，在Θ=90°時又減至0.9 kPa。隨著R/D的增大，管內流體流動方向變化緩慢，內外側靜壓差逐漸變小，Θ=45°處4種情況的靜壓差分別為1.6、1.10、0.55、0.45 kPa，外側壁面流體向內側壁面流動的推動力減小，這會導致二次流強度的消弱。

2.4 Re對內外壁靜壓分布的影響

保持R/D=1.5，研究壓力損失隨Re數的變化情況，結果見圖5。

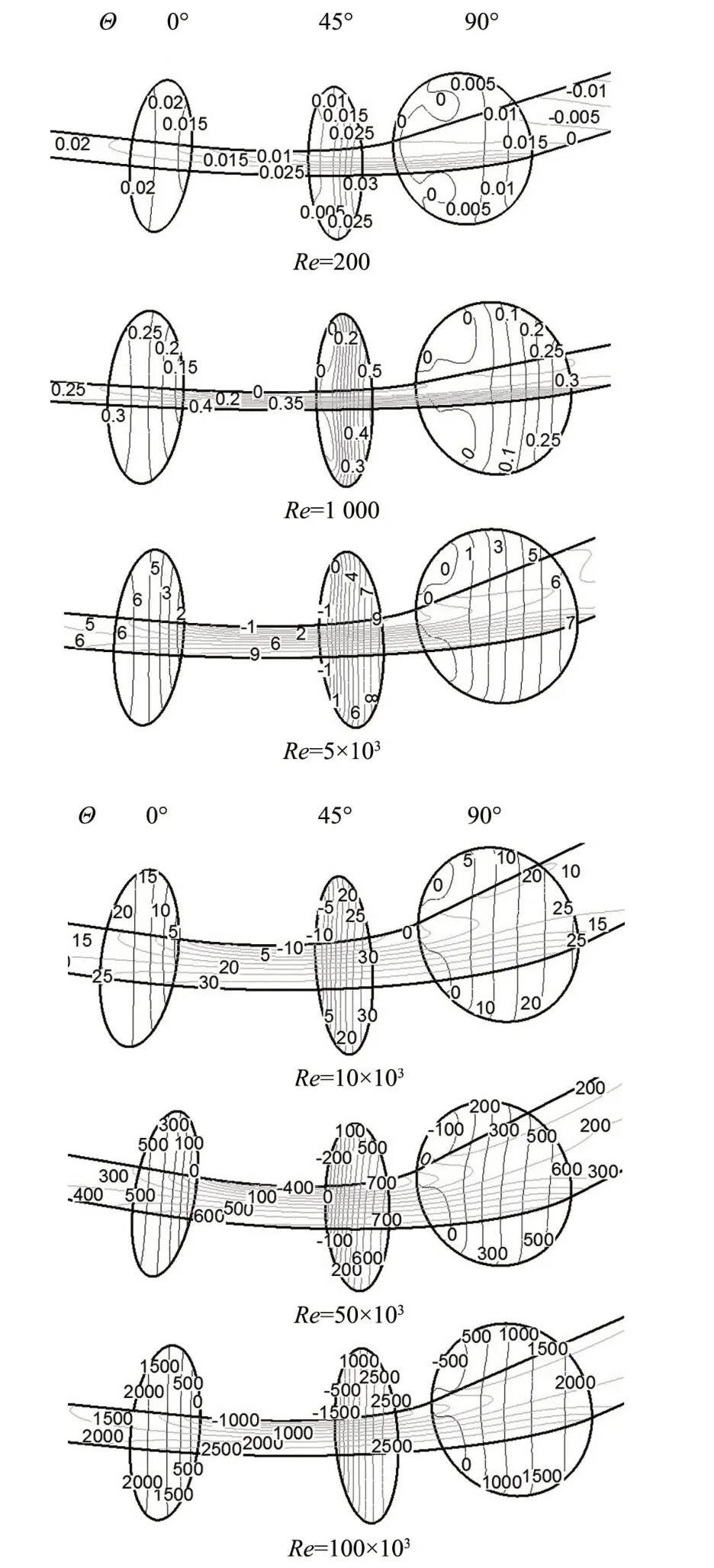
圖5 Re對內外壁靜壓分布的影響Fig 5 Effect of Re value to static pressure contribution of inside and outside wall

由圖5 可知，當流動處于層流狀態時（Re=200、1 000），管內靜壓較小，壓力損失也很小，管內外側壁面的壓力差不到1 Pa，由于壓力差造成的二次流強度將會很小。隨著Re 數的增大，流動達到湍流狀態外側壁面的靜壓力迅速增大，由10 Pa左右升至2.5 kPa，內外側壓力差也有10 Pa 左右升至4.0 kPa左右。并且最高壓力和最大壓力差都在45°左右，因此Re 數對彎管內流體內外側壓力分布有著顯著影響。

2.5 管彎曲度對二次流的影響

保持Re=50×103，研究管彎曲度對二次流的影響。均勻流體垂直進入管道，該條件下的速度云圖和二次流跡線分布見圖6。

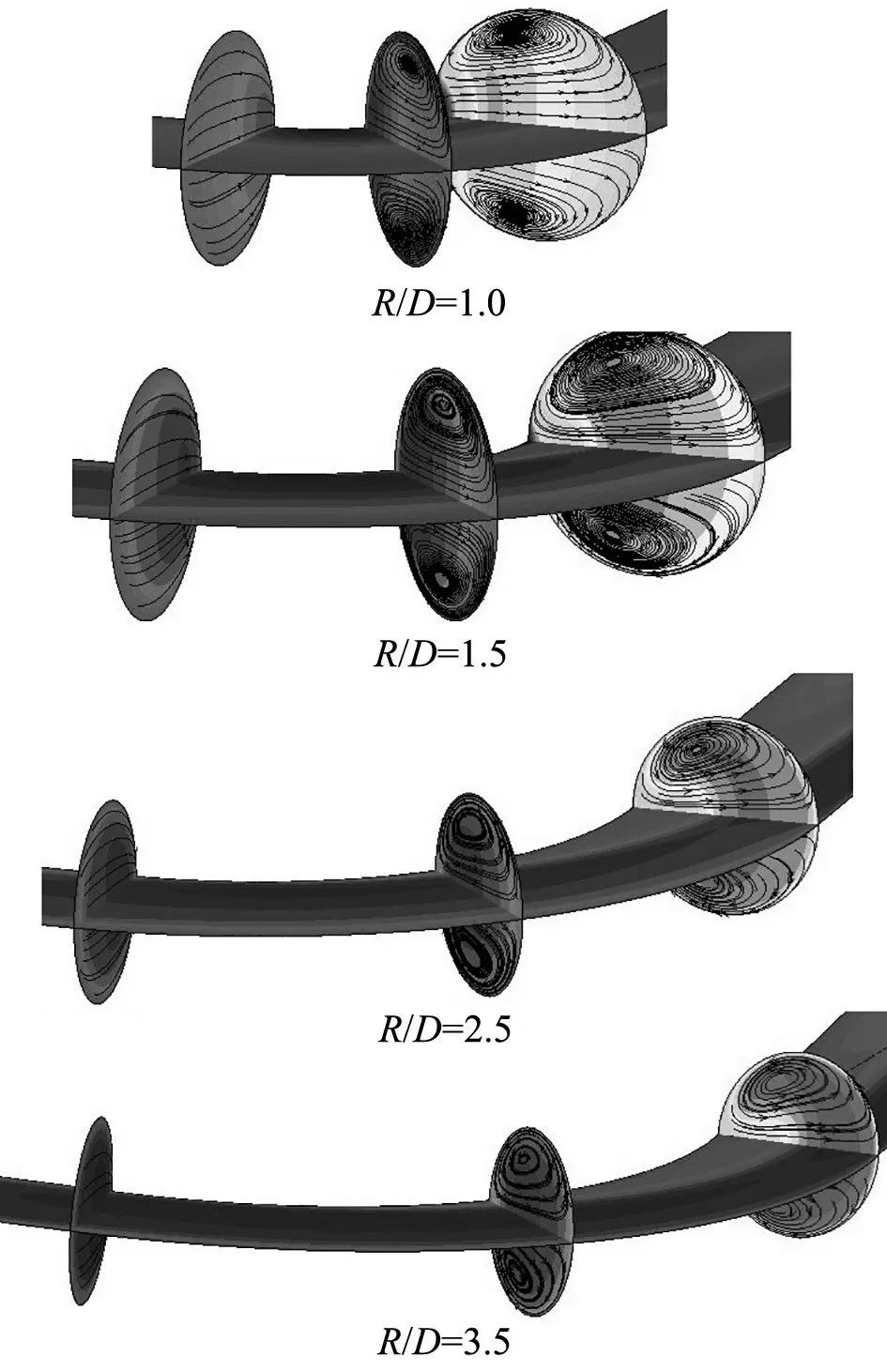
圖6 管彎曲度對二次流的影響Fig 6 effect of the pipe blend degree to the secondary flow

由圖6 可知，由于彎管的主流入口截面Θ=0°的位置受管道曲率的影響很小，因此沒有出現明顯的回流現象，二次流速度也很小。彎曲段出口截面Θ=90°上二次流速度較大，已出現一對渦流，且2個主渦的渦心靠近內側壁面，說明外側壁面附近的壓力大于內側壁面，推擠流體向內側壁面流動。彎曲段出口截面Θ=90°上二次流速度與Θ=90°位置處相近。

有研究表明，二次流在Θ=60°時強度達到最大，隨著流體向彎管下游流去，壓力梯度逐漸減小，二次流逐漸減弱，二次流圖像中主渦的渦心也會遠離內側壁面，接近外側壁面。從圖6中二次流分布也可以定性看出，R/D=1時，管彎曲程度較高，二次流強度大，隨著R/D 的增大，曲率變小，二次流強度會進一步削弱。

2.6 Re對二次流的影響

保持R/D=1.5，研究Re數對二次流的影響，見圖7。

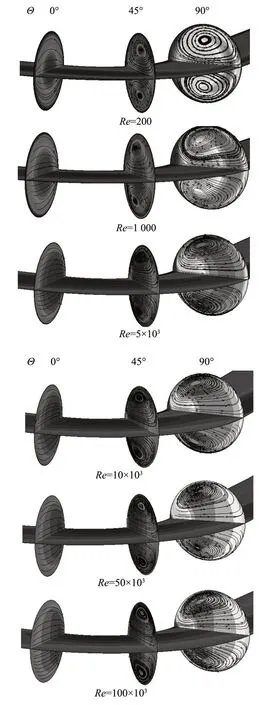
圖7 管彎曲度對二次流的影響Fig 7 Effect of Re value to the secondary flow

由圖7可知，Re數對二次流的影響通過內外壁的壓力差來體現，Re 數越大，內外側壁面的靜壓力差越大，流體受到的沿外壁向內壁的推動力也越大，致使二次流的產生，推動力越大，二次流越強。

3 結 論

本文通過Fluent軟件，標準k-epsilon模型，對90°彎曲管道內湍流流動進行數值模擬。研究了Re數和管彎曲度對管內流動壓力損失、內外側壁面壓力分布和二次流的影響。結果發現，當Re=50×103 時，總的流動阻力損失在R/D≈2.5 時達到最小；阻力系數Cp在流動處于湍流范圍時降至2 以下，更高Re數下的阻力系數在0.4～0.7，與已有研究結果相符；隨著R/D的增大，內外側靜壓差逐漸變小，Θ為45°處內外側壁面靜壓差大于Θ為0°和90°；管內流動狀態對彎管內流體內外側壓力分布有著顯著影響；二次流強度隨R/D 減小和Re 數的增大而增加。