基于加速度頻響函數小波分解的模型修正方法

彭珍瑞，曹明明，劉滿東

蘭州交通大學 機電工程學院，蘭州 730070

在航空、航天、機械、土木結構和武器系統的研制過程中，有限元仿真和試驗分析已成為2種不可或缺的重要手段[1]。但是在建模過程中的許多不確定性因素會導致有限元模型與試驗模型存在一定的差異，因此需要利用試驗模型的測試數據對有限元模型進行修正，使修正后的有限元模型能較準確地反映結構的動態特性[2]。其中，基于模態參數和基于頻響函數(FRFs)的模型修正方法較為常見[3]。相比較而言，基于頻響函數的模型修正方法直接利用測量得到的頻響函數進行模型修正不需要模態識別，從而避免了識別誤差的引入，具有一定的優越性[4]。文獻[5-6]分別從理論上介紹了設計參數型頻響函數修正法在工程應用中的優勢及局限。殷紅等[7]利用位移頻響函數結合結構損傷識別，得到了與結構實際參數相符的模型修正結果。Esfandiari等[8]采用基于頻響函數的模型修正方法，實現了對一標準桁架結構的損傷識別。楊海峰等[9]使用加速度頻響函數對一簡支梁進行了有限元模型修正。雖然基于頻響函數的模型修正方法有一定的優勢，但因其包含大量頻率點信息，所以頻率點的選擇對于修正結果有重要影響，目前尚無統一方法。Kwon和Lin[10]引入測量依賴性指標和參數依賴性指標來選擇最優頻率點。張勇等[11]利用頻響函數截斷奇異值分解進行模型修正避開了頻率點的選擇難題。

目前，作為一種可以替代有限元模型進行快速分析的代理模型技術，引起了眾多學者的關注。代理模型通過建立一個顯式的函數來代替模型參數與結構響應之間復雜的隱式關系，近年來逐漸被應用到結構模型修正與確認中[12]。常用的代理模型有響應面法(RSM)、徑向基函數(RBF)、神經網絡(NN)、支持向量回歸機(SVR)、Kriging模型等[13]。其中Kriging模型是基于Kriging插值技術的一種等效模型，與其他代理模型不同的是，Kriging模型除了能給出對未知函數的預估值，還能得到預估值的誤差估計[14]，只用少量的樣本就可以較準確地描述結構輸入與輸出間的關系，在航天飛行器設計和結構優化設計等領域應用較為廣泛。文獻[15-17]將Kriging方法應用于頻響函數模型修正中，減少了求解時間，提高了頻響函數模型修正的效率。

在上述背景下，為保留利用頻響函數進行模型修正的優點，同時避免頻率點的選擇難題和提高模型修正效率，本文提出了一種基于加速度頻響函數小波分解的模型修正方法。將計算得到的加速度頻響函數進行小波分解，用小波分解得到的第1層幅值較大的小波系數來表征頻響函數作為Kriging模型的輸出，以模型待修正參數作為Kriging模型的輸入，并通過混合灰狼算法對Kriging模型相關系數進行尋優來構建精確的Kriging代理模型。然后，以實測的加速度頻響函數小波分解得到的第1層小波系數與代理模型輸出小波系數的差值最小作為目標函數，通過水循環算法進行待修正參數的求解。最后，通過一空間桁架結構證明了本文方法的有效性，特別是對于隨機噪聲的魯棒性。

1 加速度頻響函數小波分解

1.1 加速度頻響函數

頻域內，一個n自由度阻尼系統在簡諧激勵作用下的運動方程可以表示為

(-ω2M+iωC+K)X(ω)=F(ω)

(1)

式中：M、K和C分別表示質量矩陣、剛度矩陣和阻尼矩陣；ω為激勵頻率；F(ω)為簡諧激勵；穩態響應X(ω)可表示為

X(ω)=H(ω)F(ω)

(2)

其中：H(ω)為加速度頻響函數，可表示為

(3)

1.2 小波變換

小波變換是信號處理領域的一種重要研究方法，被用于圖像壓縮、信號濾波、數據融合和特征提取等很多方面。Donoho[18]提出了小波軟、硬閾值消噪法。該方法計算量小且容易實現，得到了廣泛的關注和應用。

一維含噪信號可以表示為

y(t)=s(t)+o(t)t=0,1,…,T-1

(4)

式中：y(t)為含噪信號；s(t)為有用信號；o(t)為噪聲信號；t為采樣點；T為采樣點數，其小波變換為

(5)

其中：λjk為含噪信號的小波系數，ψ(·)為小波函數。因為小波變換是線性變換，所以式(5)可以變為

λjk=λjk(s)+λjk(o)

(6)

其中：λjk(s)和λjk(o)分別為有用信號和噪聲信號的小波系數。

小波變換特別是正交小波變換具有很強的去數據相關性，它能夠在小波域中使信號的能量集中在一些大的小波系數中；而噪聲的能量卻分布于整個小波域內。因此，經小波分解后，有用信號的小波系數幅值要大于噪聲信號的系數幅值。可以認為，幅值比較大的小波系數一般以有用信號為主，而幅值比較小的系數在很大程度上是噪聲信號[19]。對比多次試驗效果，設定小波基為db4，當無噪聲或者弱噪聲(信噪比為30 dB、20 dB)干擾時分解層數設為5，當強噪聲(信噪比為10 dB、5 dB)干擾時分解層數設為4，用加速度頻響函數經小波分解后的第1層幅值較大的小波系數作為加速度頻響函數的特征量進行模型修正。

2 基于Kriging模型的模型修正理論

2.1 Kriging模型的建立

Kriging模型是一個基于隨機過程的代理模型，最初在地質統計學中提出。模型包含了線性回歸部分和非參數部分：

(7)

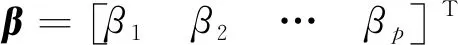
Cov [z(xi)，z(xj)]=σ2R(xi,xj)

(8)

其中：σ2為z(x)的方差；xi和xj為樣本中任意2個樣本點；R(xi,xj)是相關函數，表示樣本點間的空間相關性。選計算效率較好的高斯函數為相關函數：

(9)

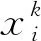
(10)

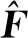
(11)

其中：n為試驗點數；σ2和β均為θk的函數，那么Kriging模型中唯一未知數即為相關系數θk，其決定著預測響應精度，本文采用混合灰狼算法對相關系數θk進行尋優。

(12)

式中：rT(x0)=[R(x0,x1)R(x0,x2)…R(x0,xn)]。

2.2 混合灰狼算法

混合灰狼算法(DE-GWO)是由Zhu等[20]提出，該算法將差分進化算法(DE)強大的搜索能力融入灰狼算法(GWO)中，使GWO能夠跳出停滯區，降低了GWO尋得局部最優值的可能性，加快了收斂速度，優于粒子群(PSO)算法、差分進化算法(DE)和灰狼算法(GWO)。算法流程如下：

1) 參數初始化。設置種群規模Npop、最大迭代次數MaxIt、自變量維數nVar、縮放因子下上界beta_min和beta_max，交叉概率pCR，參數下上界lb和ub。

2) 對種群個體進行DE變異操作，產生中間體；并進行競爭選擇操作形成父代種群、子代種群和變異種群個體。

3) 社會等級。計算種群中每個灰狼個體的適應度值，并依據適應度值的大小進行排序，確定灰狼種群中的社會等級，最優解Xα為頭狼，第2和第3最優解Xβ和Xδ為狼群中第2和第3等級狼，其余的候選解X為狼群中最低等級狼。

4) 搜索包圍獵物。灰狼搜索獵物過程中，灰狼接近并包圍獵物行為可以表示為

D=|C·Xp(t)-X(t)|

(13)

X(t+1)=Xp(t)-A·D

(14)

式中：D為灰狼與獵物之間的距離；Xp(t)和X(t)分別是第t次迭代獵物和灰狼的位置向量；C和A為系數向量，且C=2r1，A=2ar2-a，其中r1和r2為[0，1]之間的隨機向量，a是一個動態向量，隨著迭代次數的增加從2線性遞減至0。

5) 追捕獵物。當灰狼搜索到獵物所在位置時，首先，頭狼Xα帶領狼群對獵物進行包圍；然后，頭狼Xα帶領Xβ狼和Xδ狼對獵物進行攻擊捕捉。在灰狼群體中，Xα、Xβ、Xδ狼距離獵物位置最近，因此可以通過這三者的位置來計算灰狼個體向獵物移動的位置。并根據式(15)計算出種群中最優個體Xα、Xβ和Xδ與其他灰狼個體之間的距離，再根據式(16)計算出其余灰狼的移動方向。最后由式(17)更新灰狼位置。

(15)

(16)

(17)

式中：X1(t)、X2(t)和X3(t)代表最優個體Xα、Xβ和Xδ與其他灰狼個體X指導后更新的位置；X(t+1)為子代灰狼的最終尋優位置。

6) 對種群個體進行交叉、選擇操作保留優良成分并產生新子代個體，計算個體的適應度值。

7) 更新灰狼Xα、Xβ和Xδ及其他對應的位置信息。

8) 判斷是否達到最大迭代次數MaxIt，如果是則停止并輸出當前最優解，否則返回3)繼續執行。

2.3 混合灰狼算法優化Kriging模型

Kriging模型中的相關系數θk決定著預測響應值精度，只有當所建立Kriging模型精度足夠高時，代理模型對修正結果的誤差影響才會最小。所以相關系數的確定對于構建代理模型至關重要。本文采用拉丁超立方抽樣方法抽取一定數量的樣本點，然后把抽取的樣本點分成訓練集和測試集。以訓練集作為Kriging模型的輸入變量，以加速度頻響函數小波分解得到的第1層小波系數作為響應值來構建Kriging模型，以測試集Kriging模型的均方誤差(MSE)均值平均值作為混合灰狼算法的目標函數，尋得最優相關系數。最后以訓練集作為樣本點建立Kriging模型。

2.4 模型修正

當Kriging模型構造完成時，模型修正歸根結底是一優化問題，在目標函數最小的條件下，通過求解該優化問題，得到設計參數的修正值。當激勵點和響應點確定時，目標函數為

(18)

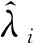
在優化求解時，除了靈敏度方法外，智能算法也是很簡便的。水循環算法(WCA)[21]的基本概念和思想來源于自然，并基于現實世界中的水循環過程，具有良好的隨機搜索能力、魯棒性和快速收斂等優點。故本文使用水循環算法進行優化求解待修正參數，模型修正流程如圖1所示。

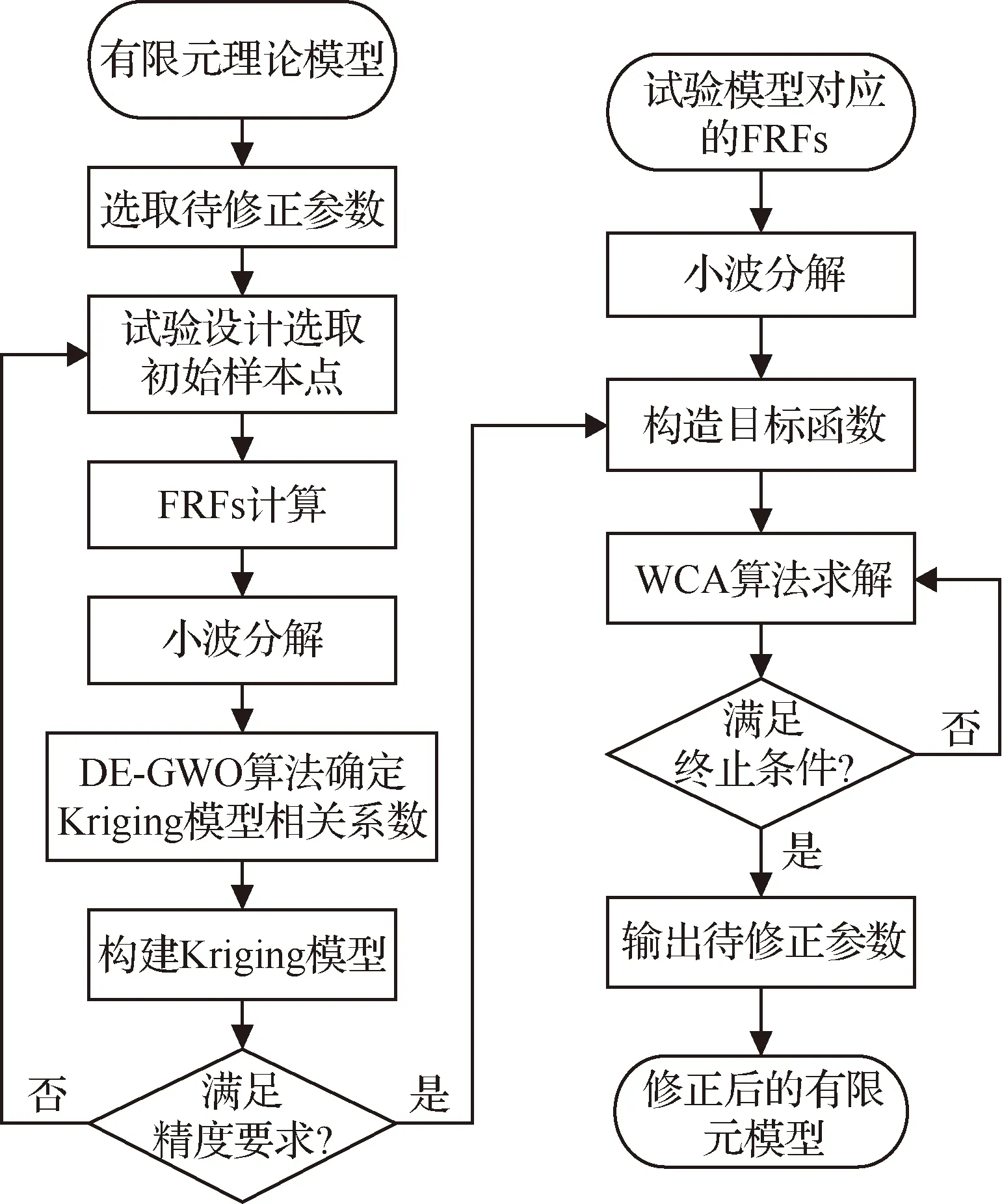
圖1 模型修正流程圖Fig.1 Flow chart of model updating

3 數值算例

選擇一空間桁架結構來驗證本文方法。該結構包括28個節點，66個單元和48個自由度。桁架約束條件為4個支座固定(節點編號:1、8、9、16)，節點鉸接，如圖2所示，桁架結構參數如表1所示。

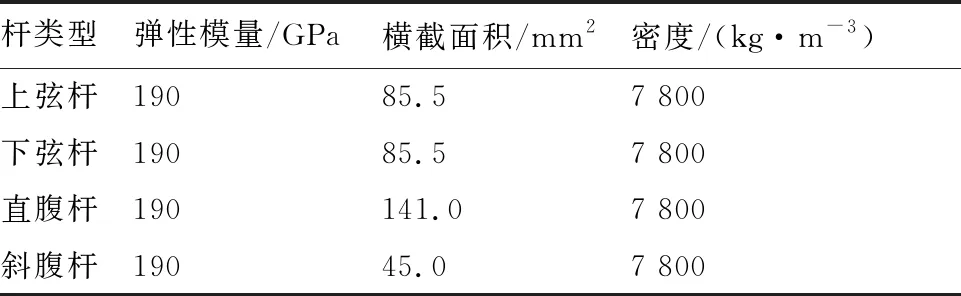
表1 三維桁架結構參數Table 1 Structure parameters of three-dimensional truss

根據樣本點參數，運用動力學方法計算其質量矩陣、剛度矩陣并且添加一定的比例阻尼，將其代入式(3)中計算出其加速度頻響函數矩陣。由于本文所用方法間接利用頻響函數，避開了頻率點選擇問題，所以在頻率點的選擇問題上，只需保證頻響函數在感興趣頻帶內有足夠數量的共振峰。所選結構的激勵點和響應點如圖2所示。

3.1 待修正參數選取與試驗設計

根據表1將各桿的彈性模量E和密度ρ、上弦桿橫截面積A1、下弦桿橫截面積A2、直腹桿橫截面積A3、斜腹桿橫截面積A4，這6個參數作為初選待修正參數。以表1中的各參數數值作為“試驗模型”參數，然后對“試驗模型”參數進行偏移得到“有限元模型”參數。其中，彈性模量E增加10%，密度ρ減小10%，上弦桿橫截面積A1增加10%，下弦桿橫截面積A2減小10%，直腹桿橫截面積A3增加10%，斜腹桿橫截面積A4減小10%，得到對應的有限元模型參數值如表2所示。

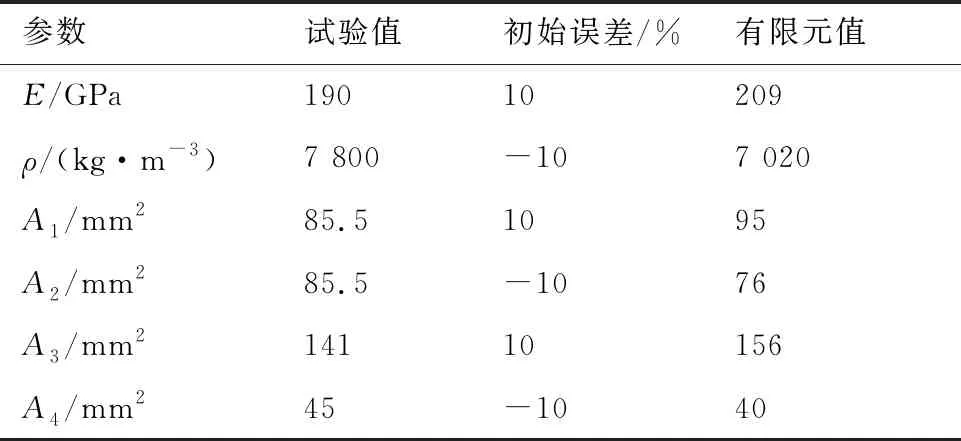
表2 試驗模型和有限元模型參數Table 2 Parameters of test model and finite element model

對于全局優化問題，比較好的方法是通過試驗設計(DoE)來選取一組樣本點。對于Kriging模型，初始樣本點數理論上不受設計空間維數的限制，且優化效率對初始樣本點數的依賴也不明顯[14]。為此，采用拉丁超立方抽樣在上述有限元模型6個參數的±20%區間內抽取200個樣本點，使所構建Kriging模型滿足精度要求。根據樣本點運用全局靈敏度中的Sobol法計算各參數對于響應的靈敏度值，將各參數靈敏度值歸一化并轉換成百分比形式，如圖3所示。

由圖3可以看出，各桿的彈性模量E、密度ρ和上弦桿橫截面積A1靈敏度最高，而其他桿的橫截面積靈敏度相對較小，所以選擇E、ρ、A1作為待修正參數進行模型修正。

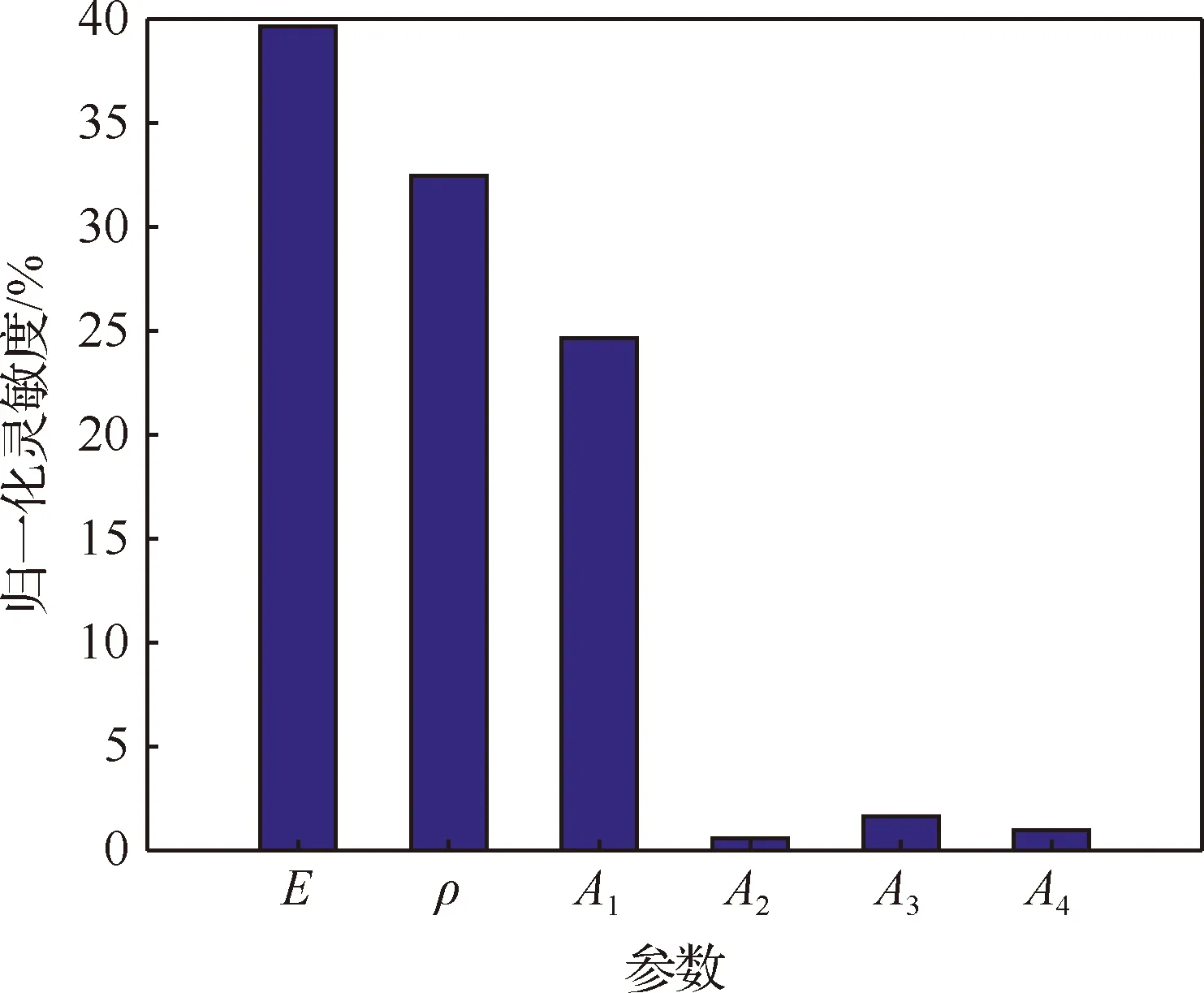
圖3 各參數靈敏度Fig.3 Sensitivity of each parameter

3.2 Kriging模型的構造及評估

基于拉丁超立方抽樣抽出的200個樣本構造Kriging模型。用前150個樣本數據作為訓練集，后50個數據作為測試集。以訓練集作為Kriging模型的輸入，以訓練集所對應的加速度頻響函數小波分解得到的第1層的小波系數作為輸出，構造初始Kriging模型。以測試集Kriging模型的均方誤差(MSE)均值平均值最小作為混合灰狼算法的個體目標函數，尋得最優相關系數θk。混合灰狼算法參數設置：種群規模Npop=40，最大迭代次數MaxIt=300，自變量維數nVar=1，縮放因子上下界beta_max和beta_min分別為0.2和0.8，交叉概率pCR=0.2，參數上下界ub和lb分別為0.01和100。最終尋得最優相關系數為0.875 8，迭代曲線如圖4所示。

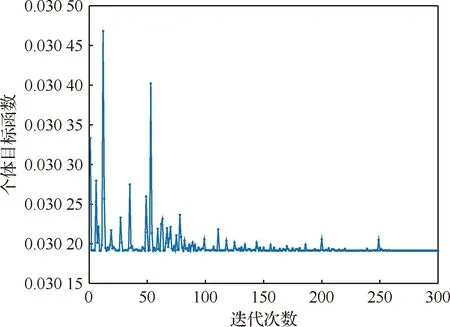
圖4 混合灰狼算法迭代曲線Fig.4 Iteration curve of DE-GWO

由圖4可以看出，當迭代次數增加至250次時，迭代曲線基本收斂，尋得最優值。相關系數確定以后，就可以構造Kriging模型。為評估所構建Kriging模型的精度，訓練集樣本第5個小波系數真實值和Kriging模型預測值的擬合曲線如圖5所示。為進一步評估Kriging模型的預測精度，測試集樣本第10個小波系數真實值和Kriging模型預測值的擬合曲線如圖6所示，并根據式(19) 計算出小波系數真實值和Kriging模型預測值間的均方根誤差(RMSE)，當RMSE越接近0時Kriging模型預測精度越高。

(19)

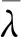
由圖5看出，通過訓練集構建的Kriging模型預測值和真實值幾乎重合，表明訓練集的擬合精度很高。訓練集的擬合精度并不能說明Kriging模型預測精度，必須用訓練集以外的樣本點來驗證Kriging模型的預測精度，本文用測試集樣本來驗證。由圖6看出，除個別樣本點外，測試集樣本點對應的Kriging模型預測值幾乎和真實值重合，并且通過式(19)計算出的RMSE值為8.164 1×10-4，表明所構建的Kriging模型預測精度很高，可以代替理論模型進行模型修正。

圖5 訓練集樣本第5個小波系數預測值Fig.5 Predicted value of the fifth wavelet coefficient of training set sample

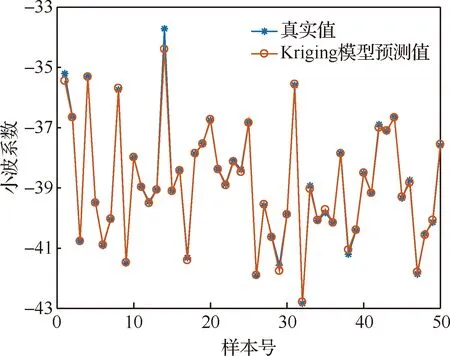
圖6 測試集樣本第10個小波系數預測值Fig.6 Predicted value of the 10th wavelet coefficient of test set sample

3.3 模型修正

當完成Kriging模型構造以后，就可以根據式(12)通過水循環算法以式(18)作為目標函數迭代求解待修正參數。假定試驗參數值在有限元參數值的±20%區間內，使用水循環算法進行迭代尋優。水循環參數設置：雨滴層數為50，河流和大海個數總和為4，極小值為1×10-5，最大迭代次數為100。修正結果如表3所示，水循環迭代曲線如圖7所示。

由圖7可以看出水循環算法具有良好的搜索能力和快速收斂性能，算法在10次迭代以前就已收斂。多次運行尋優程序，迭代曲線基本不變化，也表明了該算法尋優的魯棒性。由表3可以看出，用本文所提方法進行模型修正取得了很好的修正效果。使用表3中的各參數試驗值和有限元值計算出試驗模型和有限元模型對應的加速度頻響函數。使用所得修正參數的平均修正值計算得到修正后的加速度頻響函數，稱其為Kriging模型加速度頻響函數。Kriging模型、試驗模型及有限元模型加速度頻響函數曲線如圖8所示。

表3 模型修正參數及其誤差Table 3 Parameters and their errors of model updating

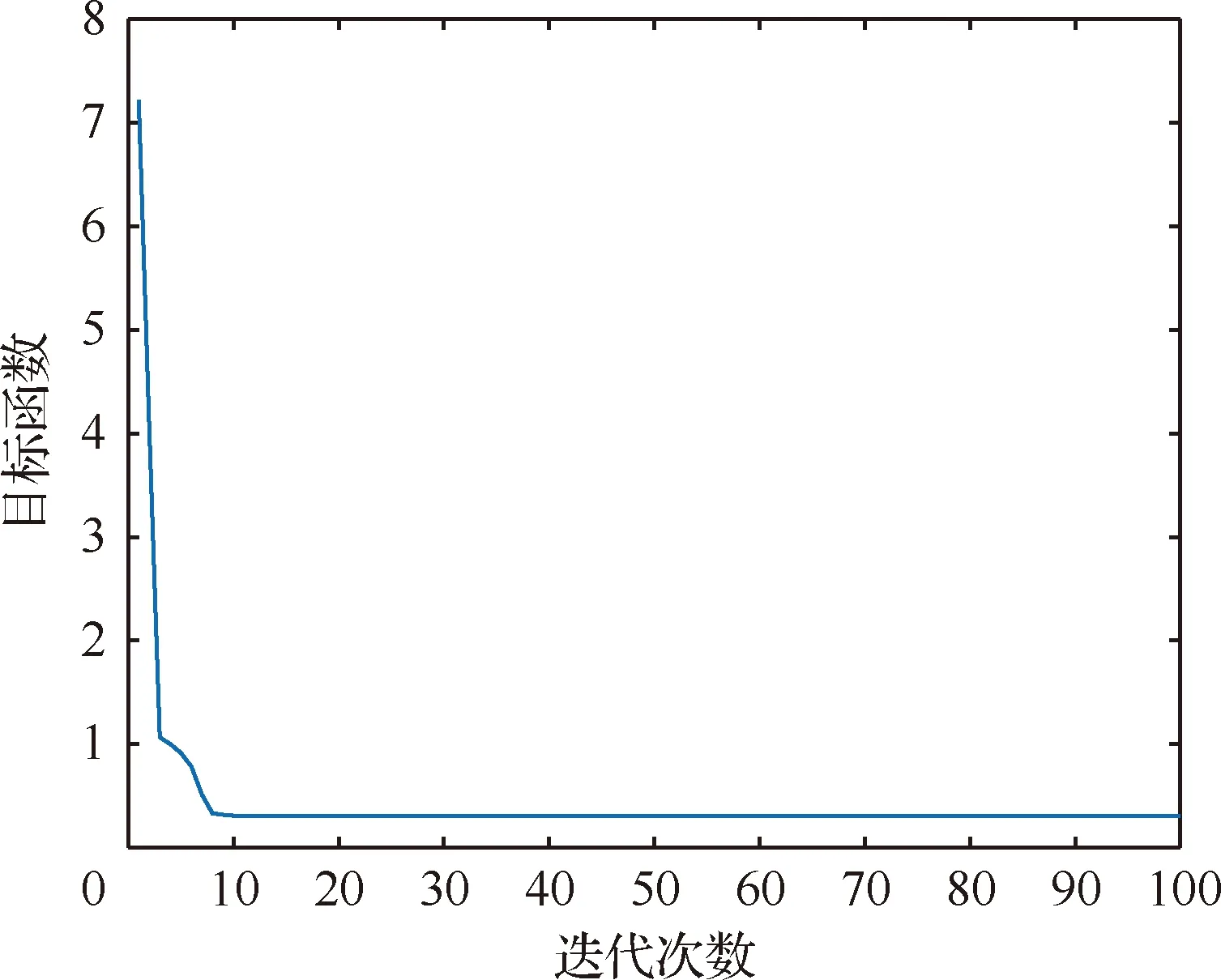
圖7 水循環迭代曲線Fig.7 Iteration curve of WCA

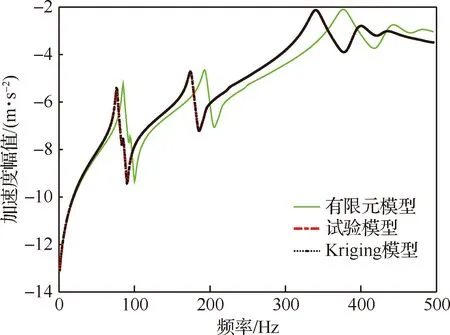
圖8 Kriging模型、試驗模型及有限元模型頻響函數曲線Fig.8 FRF curves of Kriging model, test model and finite element model

由圖8可以看出修正過后的結構加速度頻響函數曲線與試驗加速度頻響函數曲線幾乎重合，與有限元模型加速度頻響函數曲線形狀相似，只是沿坐標軸有一定的移動。

為進一步檢驗本文修正方法的修正效果，比較頻響函數修正前后實、虛部曲線，如圖9所示。由圖9可以看出修正后的有限元模型無論是實部還是虛部，都能很好地與試驗模型的頻響函數曲線重合。這進一步證明了本文所提方法的有效性。

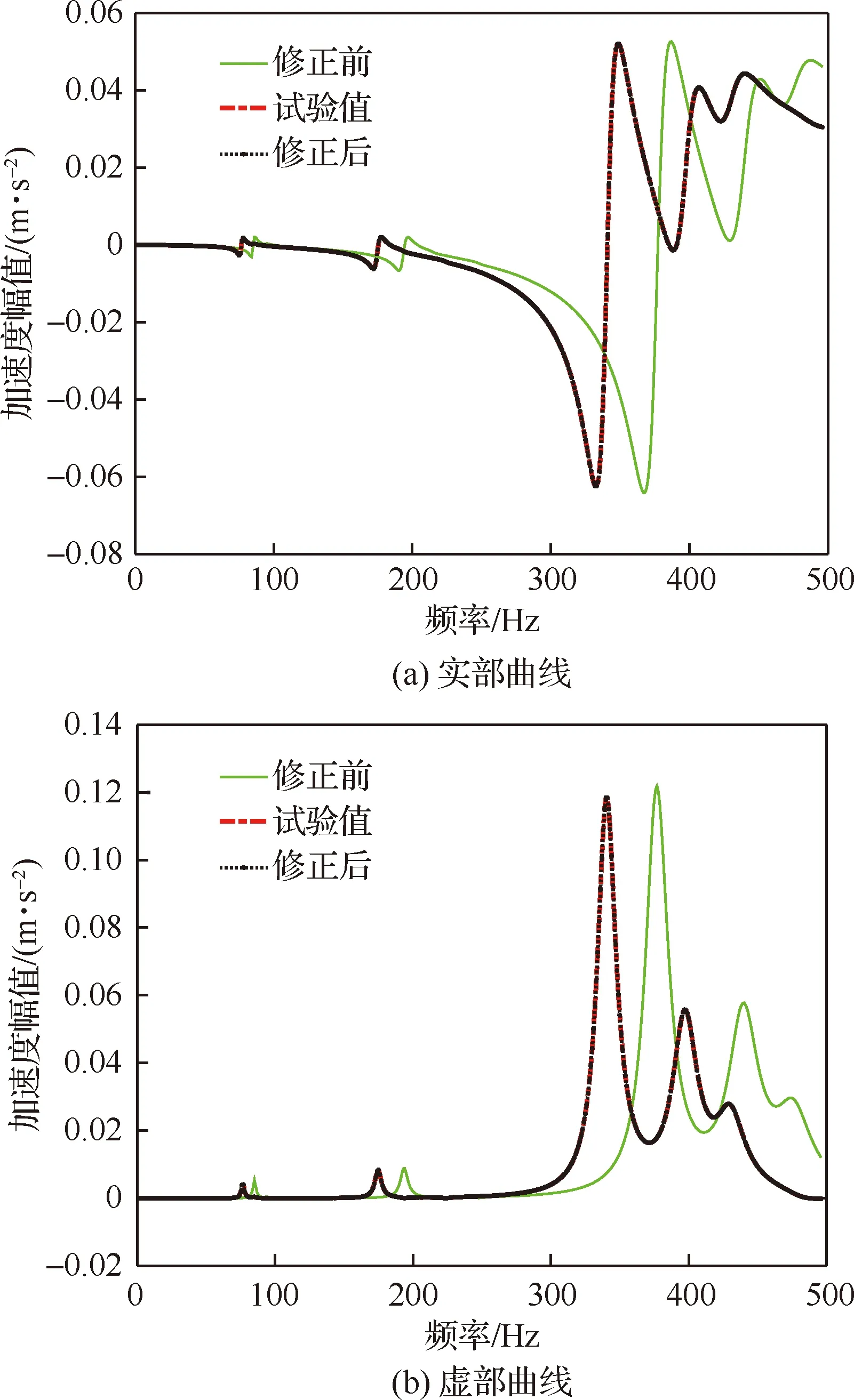
圖9 修正前后頻響函數曲線Fig.9 FRF curves before and after updating

實測試驗時目標頻響函數不可避免會受到隨機噪聲的干擾，在一些特殊環境下外界噪聲干擾還很大。所以在計算的試驗頻響函數中加入信噪比為30、20、10和5 dB的高斯白噪聲，來驗證本文方法對于噪聲的魯棒性。圖10為加入信噪比為20 dB和5 dB時加速度頻響函數圖。

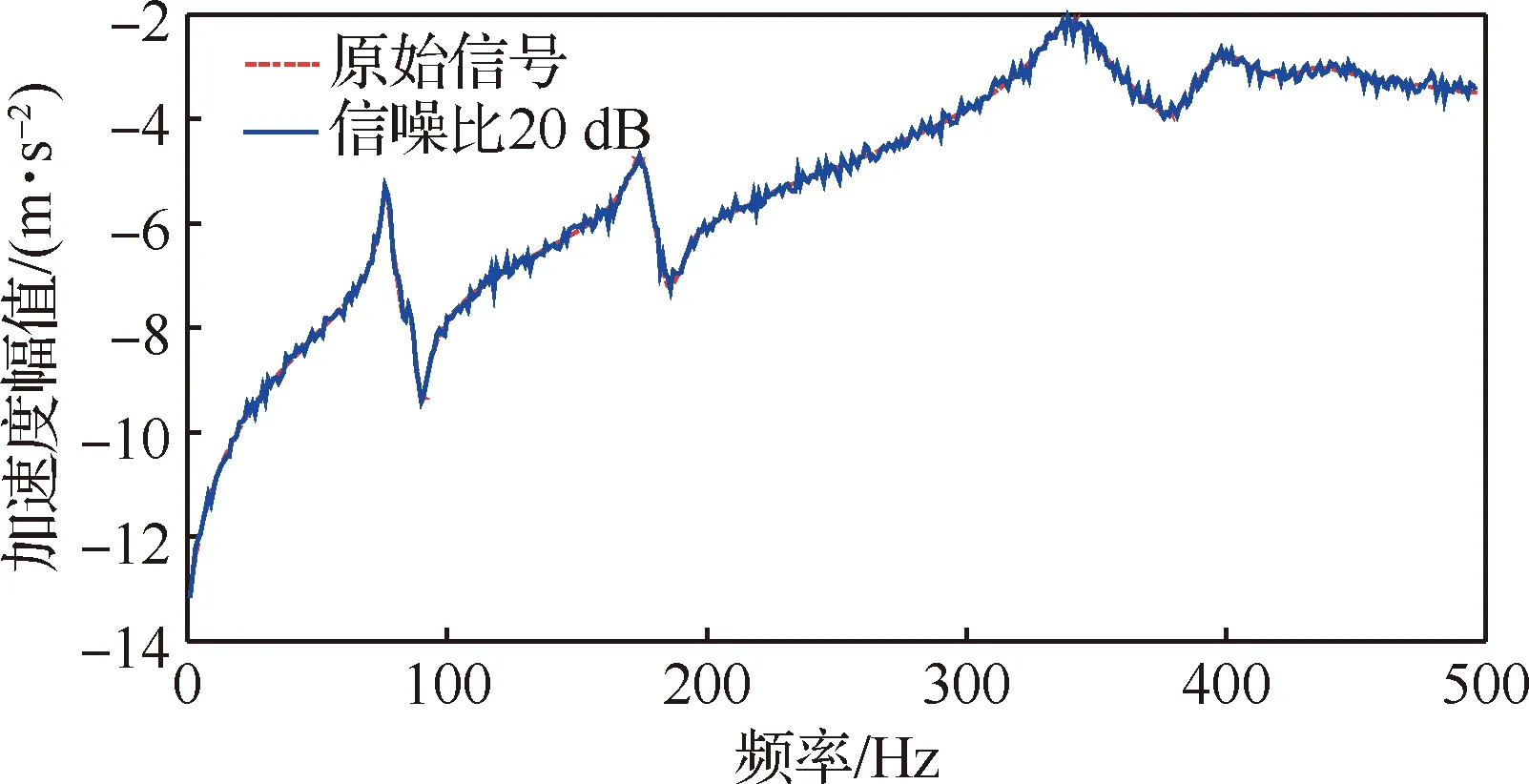
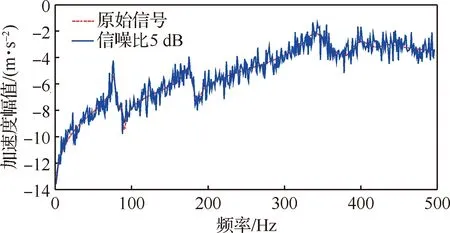
圖10 20 dB和5 dB信噪比下加速度頻響函數Fig.10 FRF under 20 dB and 5 dB SNRs

將加入噪聲的加速度頻響函數按前文所提小波參數設置方法進行小波分解，得到不同信噪比下小波系數曲線和局部放大曲線，如圖11所示。由圖11可以看出，將加速度頻響函數進行小波分解以后得到的序號較小的小波系數幅值較大，而絕大部分小波系數趨近于0。當在信號中加入隨機噪聲時，隨著加入的高斯白噪聲信噪比逐漸減小，對于幅值較大的小波系數影響較小，而對于幅值小的小波系數干擾較大。為了更直觀地看出不同信噪比下噪聲對于小波系數的影響，將小波系數隨小波系數序號的變化分成3個部分，如各圖中的3個放大曲線所示。放大曲線中左側為加速度頻響函數小波分解得到的第1層小波系數，個數較少，幅值較大；右上為加速度頻響函數小波分解得到的中間靠前的小波系數，個數中等，幅值有大有小；右下為加速度頻響函數小波分解得到的中間靠后的小波系數，個數較多，幅值趨近于0。

根據圖11(a)～圖11(d)，由其中的左側放大曲線可以看出第1層小波系數曲線隨著加入的噪聲加大，加噪小波系數曲線與未加噪小波系數曲線相似，大部分重合，只是當噪聲很大時略有波動。由右上放大曲線可以看出，隨著噪聲的加大幅值大的小波系數曲線波動較小，而幅值小的小波系數曲線波動開始加大。由右下放大曲線可以看出，隨著噪聲的加大對于幅值趨近于0的小波系數影響較大，噪聲越大小波系數曲線波動越大。綜上所述，加速度頻響函數經小波分解后得到較少數目幅值較大的小波系數，絕大部分小波系數趨近于0。當加速度頻響函數受到噪聲干擾時，對于幅值較大的小波系數干擾較小，而對于幅值較小的小波系數干擾較大。

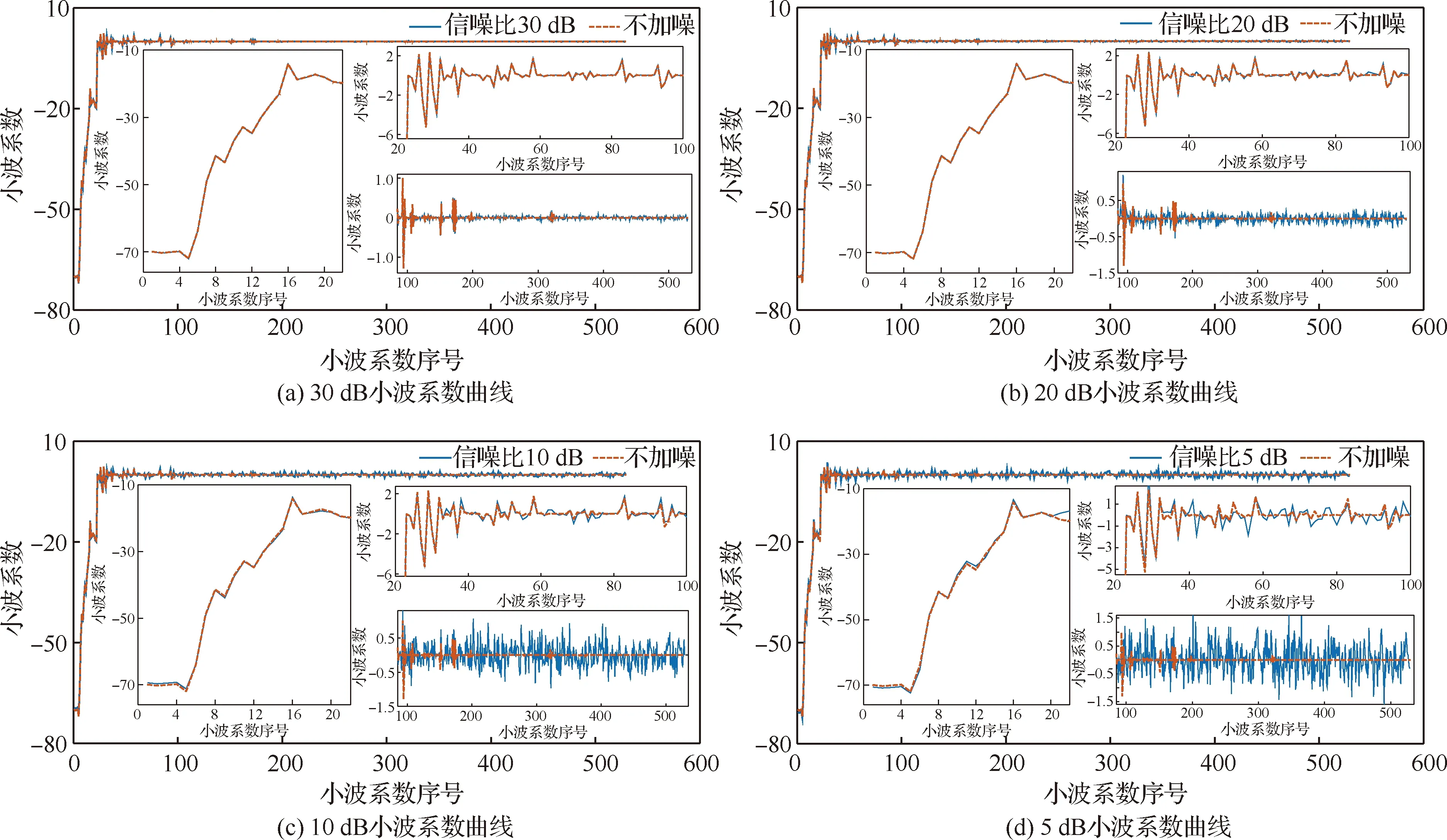
圖11 不同信噪比下小波系數曲線和局部放大圖Fig.11 Wavelet coefficient curves and local enlarged curves under different SNRs

在不同噪聲水平下連續運行10次程序的模型修正結果均值如表4所示。由表可以看出/有無噪聲對于模型修正結果影響很大，而當在有噪聲情況下，隨著噪聲的加大用本文所述方法仍然能夠得出較滿意的模型修正誤差，即使當信噪比低至5 dB時，各參數模型修正誤差仍然低于4%。由此證明了本文所提模型修正方法對于噪聲具有較強的魯棒性。

表4 不同信噪比下修正結果Table 4 Updating results under different SNRs

4 結 論

1) 將小波分解引入頻響函數模型修正中，既保留了利用頻響函數進行模型修正無需進行模態識別的優點，同時也避開了頻響函數中頻率點的選擇難題。

2) 在構造Kriging模型時，用混合灰狼算法對Kriging模型相關系數進行尋優，使所構造的Kriging模型具有良好的擬合精度和預測能力，能代替有限元模型進行迭代計算，提高了模型修正效率。

3) 將加速度頻響函數進行小波分解，用幅值較大的小波系數來表征頻響函數進行模型修正，修正效果較好。算例表明，在不同噪聲水平下，使用本文所提方法仍然可以得出較滿意的修正效果，即使當信噪比低至5 dB時，各參數修正誤差仍然低于4%，證明了本文所提方法對于強噪聲的魯棒性。