異構多智能體系統(tǒng)分組輸出時變編隊跟蹤控制

田磊，趙啟倫，董希旺,4,*，李清東，任章,4

1. 北京航空航天大學 自動化科學與電氣工程學院，北京 100083 2. 北京航空航天大學 飛行器控制一體化技術國防科技重點實驗室，北京 100083 3. 北京電子工程總體研究所，北京 100854 4. 北京航空航天大學 大數據科學與腦機智能高精尖創(chuàng)新中心，北京 100083

隨著科學技術的快速發(fā)展，世界各軍事大國高度重視無人作戰(zhàn)系統(tǒng)精確協同配合能力。由無人機、無人車組成的空地異構無人作戰(zhàn)系統(tǒng)， 由于兼具無人機響應速度快、偵查范圍廣、通信能力強的特點以及無人車負載能力強、對地目標偵查精度高的優(yōu)點，越來越受到各軍事強國的青睞。

協同控制技術是空地異構無人作戰(zhàn)系統(tǒng)實現優(yōu)勢互補與戰(zhàn)斗力有機融合的基礎，得到了廣泛的重視和研究，近年來涌現出了豐富的研究成果。而編隊控制作為協同控制的基礎性研究之一，也取得了長足的發(fā)展。相比于單一個體，集群系統(tǒng)通過個體間的相互協作，能夠以更小的代價完成難度、復雜度較高的任務，實現“1+1>2”的效果。例如，多個功能單一的衛(wèi)星可以通過協同構成一個虛擬衛(wèi)星，來完成更加復雜的深空探測任務[1]，多架無人機保持編隊隊形可以有效減小空氣阻力，降低燃料消耗[2]。另外，編隊控制在協同圍捕，協同打擊，協同偵查方面也有重要的應用[3]。相比于集中式的控制策略，分布式控制策略的可擴展性和靈活性更高，計算效率更快[4]。一致性理論的發(fā)展為分布式編隊的控制方法提供了理論支撐[5]。文獻[6-8]給出了不同情況下基于局部鄰居通信的編隊控制協議。

在協同偵查、協同打擊等任務中，無人作戰(zhàn)系統(tǒng)在形成既定編隊的基礎上，還需要能夠識別復雜多變的戰(zhàn)場環(huán)境，快速穿越柵欄、防御工事等障礙物。因此，如何控制整個編隊移動也是十分值得關注的問題，即編隊跟蹤問題。文獻[9-11]分別采用滑模控制、魯棒控制、自適應控制等方法，研究了單一智能體小組在不同條件下的時變編隊跟蹤問題，具有較好的實踐應用價值。需要指出的是，單一編隊能夠解決的問題相對有限，大多數情況下，需要將系統(tǒng)中的智能體分為多個小組，通過小組間的相互協作，完成不同的任務。例如，在無人機協同攻擊任務中，為提高突防能力與毀傷效能，需要先摧毀敵方的預警雷達、防空導彈發(fā)射陣地等防御系統(tǒng)，再摧毀指揮中樞等關鍵目標。相同小組內的無人機執(zhí)行同一個任務，而不同小組之間的無人機則借助組間無線通信技術，在智能任務目標分配與自主決策規(guī)劃的基礎上，可采取不同的戰(zhàn)術隊形對各自的目標發(fā)動進攻。文獻[12-13]給出了能夠解決分組編隊控制問題的控制協議，但各個小組獨立性強，組間協同不明顯。分組編隊控制與編隊跟蹤控制結合所產生的分組編隊跟蹤問題目前仍是開放性問題，相關研究成果尚不多見。無人機協同探測、巡航、偵查等任務[14]都可以看作分組編隊跟蹤控制問題。

此外，已有研究成果大多以同構智能體模型為前提，即每個智能體的動力學模型是相同的，考慮到無人機與無人車的動力學模型存在較大差異性，文獻[6-13]中的方法較難直接實現空地無人系統(tǒng)的協作配合，因此需要針對異構多智能體系統(tǒng)模型進行研究。文獻[15-17]研究了異構多智能體系統(tǒng)的編隊跟蹤控制問題，但是文獻中的領導者不存在控制輸入，即整個系統(tǒng)的運動軌跡不能得到有效控制。文獻[18-20]研究了領導者存在控制輸入情況下的一致性問題，但系統(tǒng)模型不是異構的或系統(tǒng)的通信拓撲關系為無向連接，工程應用性受到一定限制。

為應對異構無人系統(tǒng)在有向通信下協作與配合帶來的挑戰(zhàn)，本文研究了高階異構多智能體系統(tǒng)在有向拓撲條件下的分組輸出時變編隊跟蹤控制問題。本文的主要貢獻有：①采用全新的分組模型架構，組間和組內的協同作用明顯，并且采用有向通信拓撲結構，減小通信帶寬需求。②系統(tǒng)中的智能體均采用異構體模型，設計的控制協議能夠解決異構高階線性系統(tǒng)的分組輸出時變編隊跟蹤控制問題，同時給出了該控制協議有效性的相關證明。

1 預備知識和問題描述

1.1 圖論知識

拉普拉斯矩陣可以用來表征通信網絡中各節(jié)點的連接關系。一個有q個節(jié)點的有向圖G可以表示為G=(?,)，其中?={ι1,ι2,…,ιq}表示節(jié)點的集合，?{(ιi,ιj):ιi,ιj∈?}表示邊的集合。用Ni來表示節(jié)點ιi鄰居的集合。圖G的鄰接矩陣可以表示為W=[wij]∈Rq×q，當ιj∈Ni時，wij=1，否則wij=0。定義圖G的度矩陣為進而拉普拉斯矩陣為L=D-W。如果圖G中某一個節(jié)點到其他所有節(jié)點都存在有向連接，則稱為圖G中包含一個以該節(jié)點為根的生成樹。

1.2 問題描述

本文中的系統(tǒng)模型設計為3層架構，包含1個 虛擬領導者、M個分組領導者和N個跟隨者。所有智能體的模型可統(tǒng)一寫為

(1)

式中：i=1,2,…,1+M+N；xi(t)∈Rni、ui(t)∈Rmi和yi(t)∈Rp分別為所對應智能體的狀態(tài)、控制輸入和輸出;Ai∈Rni×ni為系統(tǒng)矩陣;Bi∈Rni×mi為輸入矩陣;Ci∈Rp×ni為輸出矩陣。

注釋1在實際物理系統(tǒng)中，單個智能體的控制輸入一定是有界的，不會是無限值，因此假設1 是合理的。

假設2輸入矩陣Bi為列滿秩矩陣，即滿足rank(Bi)=mi，并且(Ai,Bi)可鎮(zhèn)定，(Ci,Ai)可檢測，其中i=1,2,…,1+M+N。

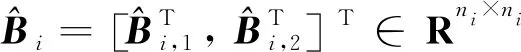
假設3有向圖G中包含一個以虛擬領導者為根節(jié)點生成樹，同時N個跟隨者被分成M個小組，每個小組有且只有一個分組領導者，虛擬領導者和分組領導者之間是單向通信，虛擬領導者與跟隨者之間不存在直接通信，分組領導者與其他分組領導者和其所在小組的跟隨者通信，跟隨者只與其所在小組的分組領導者和跟隨者通信。

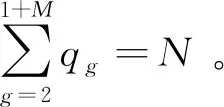
(2)

式中：LG,1、Lgro,1表征虛擬領導者與所有分組領導者之間的拓撲關系，相應的LG,g、Lgro,g表征分組領導者g與其所在小組的所有跟隨者之間的拓撲關系。

注釋2系統(tǒng)的拉普拉斯矩陣只有在假設跟隨者為順序標號時才能寫成式(2)中的形式。需要指出的是，即便跟隨者是亂序標號，但只要假設2 成立，通過簡單的行列變換即可得到形如式(2) 矩陣形式。為方便后續(xù)表達，系統(tǒng)的拉普拉斯矩陣均采用式(2)的形式。

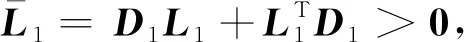
假設4對于分組領導者g=2,3,…,1+M，調節(jié)器方程:

(3)

存在矩陣對解(Eg,Fg)；對于跟隨者j=2+M,3+M,…,1+M+N，調節(jié)器方程:

(4)

存在矩陣對解(Ej,Fj)。

假設5對于分組領導者g=2,3,…,1+M，線性矩陣方程:

BgHg-EgB1=0

(5)

存在解Hg； 對于跟隨者j=2+M,…,1+M+N，線性矩陣方程:

(6)

存在解Hj。

定義1對于任意給定的有界初始狀態(tài)，如果式(7)關系成立，則稱多智能體系統(tǒng)實現了分組輸出時變編隊跟蹤控制。

(7)

式中：hg(t)、hj(t)分別為分組領導者層和跟隨者層期望實現的輸出時變編隊。

2 控制協議的設計和系統(tǒng)穩(wěn)定性分析

本節(jié)將給出控制協議的設計方法，對分組領導者和跟隨者分開進行設計。

1) 對于分組領導者g=2,3,…,1+M，設計如下控制協議：

(8a)

(8b)

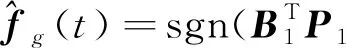
(8c)

(8d)

βgHgfg(t)+vg(t)

(8e)

(8f)

(8g)

2) 對于跟隨者j=2+M,…,1+M+N，控制協議設計為

(9a)

(9b)

(9c)

(9d)

(9e)

(9f)

βjHjfj(t)+vj(t)

(9g)

(9h)

(9i)

算法1對于智能體i∈{2,3,…,1+M+N}，控制協議(8)、(9)采用以下步驟確定部分參數值。

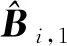
步驟3設計Ei、Fi和Hi使得矩陣方程(3)～(6)成立。

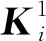
步驟5求下列Lyapunov方程的正定實對稱解陣Qi∈Rni×ni：

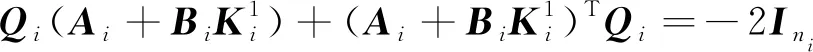
(10)

式中：Ini為ni×ni維單位陣。

算法2對于分組領導者g=2,3,…,1+M，求下列黎卡提方程的正定實對稱解陣P1∈Rn1×n1：

(11)

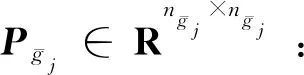
(12)

定理1如果假設4和假設5成立，分組領導者采用控制協議(8)，跟隨者采用控制協議(9)，且以下時變編隊可行性條件可以滿足:

(13)

式中：i=2,3,…,1+M+N，則異構多智能體系統(tǒng)能夠實現在有向拓撲條件下的分組時變編隊跟蹤控制。

證明：證明分為2個部分，首先證明觀測器(8a)和(9a)的收斂性，進而證明在控制器(8e)和(9g)的作用下，異構多智能體系統(tǒng)能夠實現在有向拓撲條件下的分組時變編隊跟蹤控制。對分組領導者和跟隨者分開進行討論：

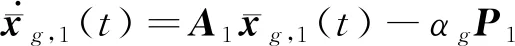
(14)

令

其中:1M表示元素全為1的M維列向量，進而可將式(14)改寫為

(15)

(16)

構造Lyapunov函數:

(17)

對Va,1(t)求導可得

(18)

由于βg>γ且以下關系式成立：

(19)

(20)

式中:g,k∈{2,3,…,1+M}，進而推出

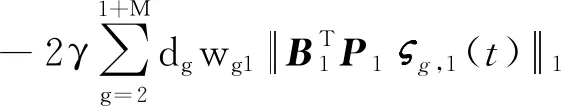
(21)

同理可以推出

(22)

由式(19)、 式(21)以及式(22)可得

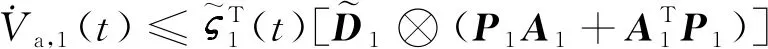
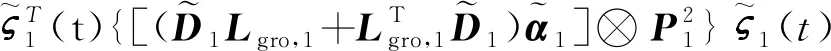
(23)

根據引理2、算法1的步驟2和算法2可知

(24)

(25)

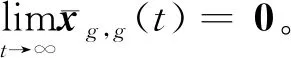
(26)

(27)

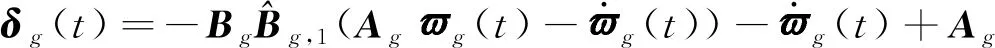
(28)

如果假設4和假設5成立，根據式(3)、式(5)和算法1中的步驟4,可將式(28)進一步化簡為

(29)

考慮如下Lyapunov函數:

(30)

式中:g=2,3,…,1+M。對Vg,1(t)求導可得

(31)

式中:

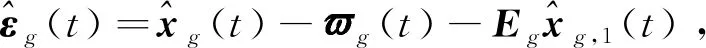
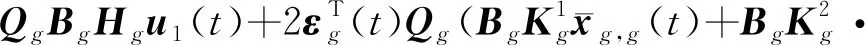
(32)

(33)

將式(32)、式(33)代入式(31)中并根據式(10)和式(30)可得

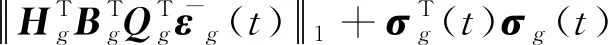
(34)

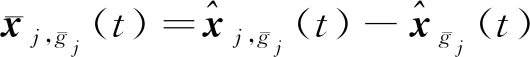
(35)

令

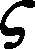
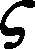
式(35)可改寫為

(36)

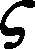
(37)

構造Lyapunov函數:

(38)

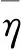
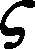
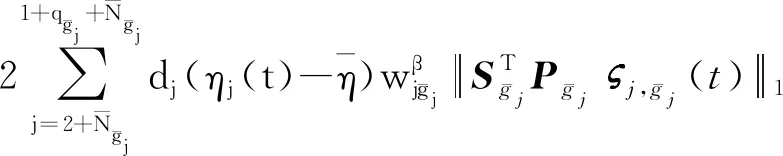
(39)

由于βj>γ且以下關系式成立:

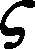
(40a)

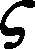
(40b)

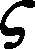
(41a)

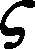
(41b)

(42a)

(42b)

(43a)

(43b)

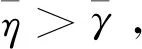
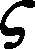
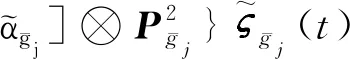
(44)

根據引理2、算法1和算法3可知

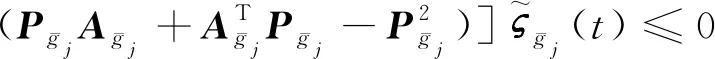
(45)

(46)

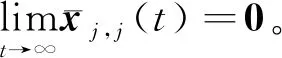
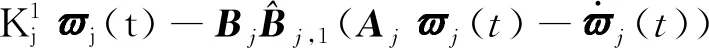
(47)

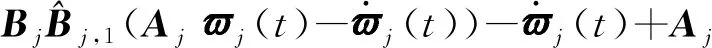
(48)

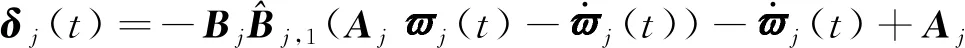
βjBjHjfj(t)

(49)

如果假設4和假設5成立，根據式(4)、式(6)和算法1中的步驟4可將式(49)進一步化簡為

(50)

考慮下列Lyapunov函數:

(51)

(52)

式中：

(53)

令

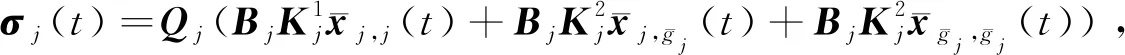
(54)

將式(53)和式(54)代入式(52)中,并根據式(51)可得

(55)

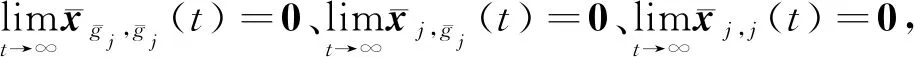
綜合上述2種情況并根據定義1可知，異構多智能體系統(tǒng)能夠實現在有向拓撲條件下的分組輸出時變編隊跟蹤控制。證畢。

3 數值仿真

為了更貼合工程實際背景，考慮由1個虛擬領導者、10架無人機、5輛無人車組成異構多智能體系統(tǒng)完成空地協同搜索任務，其中2架無人機與1輛無人車為分組領導者，其余為跟隨者。根據文獻[22]可知，四旋翼無人機模型的系統(tǒng)矩陣可近似為同理根據文獻[23]可知，麥克納姆輪無人車模型的系統(tǒng)矩陣可近似為AR=0、BR=1、CR=1。虛擬領導者的模型也采用文獻[22]中的無人機模型。

事實上，本文所研究的方法可以適用到任意可近似線性化的物理模型中。為了獲得更加直觀性的驗證效果，仿真中考慮異構多智能體系統(tǒng)在三維慣性空間的運動。虛擬領導者的初始位置設定在(-4,0,0)，在OX軸、OY軸和OZ軸方向上的初始速度分別設定為0、-4和0。10架無人機和5輛無人車在OX軸和OY軸方向上的初始位置在(-5,5)中隨機選取，在OZ軸方向上的初始位置和各軸方向上的初始速度為0，即模擬無人機和無人車由靜止狀態(tài)進行空地協同搜索的過程。

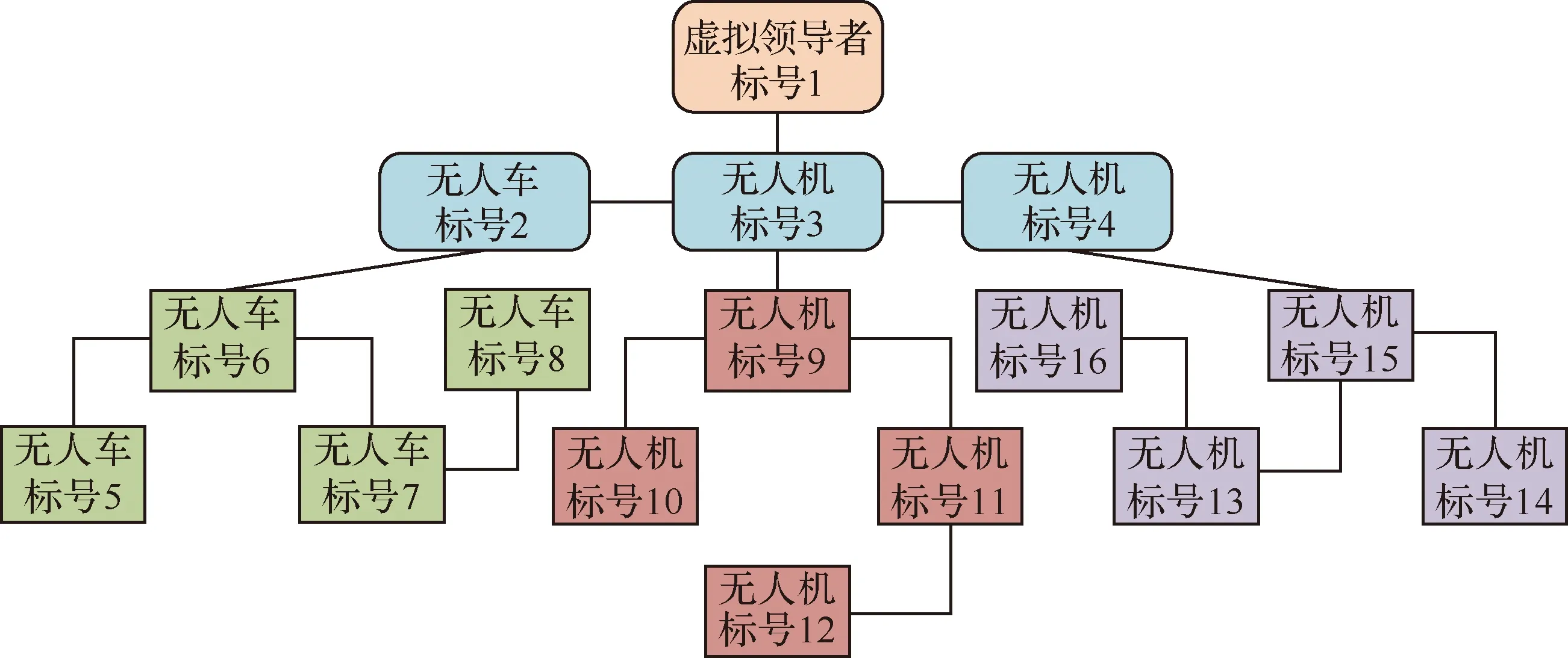
圖1 異構多智能體系統(tǒng)模型架構示意圖Fig.1 Model structure of heterogeneous multi-agent systems

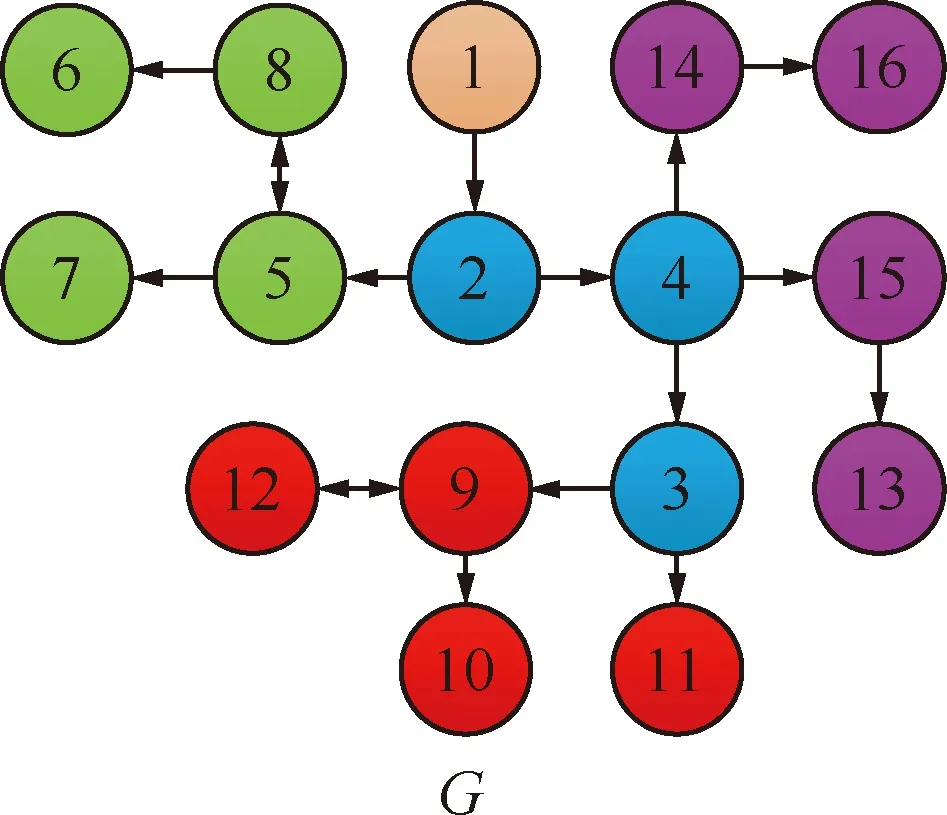
圖2 異構多智能體系統(tǒng)通信拓撲關系Fig.2 Interaction topologies of heterogeneous multi-agent systems

根據算法1、算法2和算法3，得到以下參數值：

αi=10i=2,3,…,16

βi=10i=2,3,…,16

E2=[1, 0],Ei=1i=5,6,7,8

Ei=I2i=3,4,9,10,…,16

F2=[0, 1],Fi=0i=5,6,7,8

Fi=[0, 0]i=3,4,9,10,…,16

H2=0,Hi=1i=3,4,…,16

Si=-1i=2,5,6,7,8

Si=[-2,-1]Ti=3,4,9,10,…,16

P2=1

整個多智能體系統(tǒng)的搜索軌跡如圖3中虛點所示，圖中還包括虛擬領導者，無人機和無人車在t=0, 8, 16 s時的位置信息，其中虛擬領導者用黑色星號表示，一組無人機用實心五角形表示，另一組無人機用實心六角形表示，無人車用實心圓來表示，區(qū)別是作為分組領導者的無人機和無人車用藍色表示，作為跟隨者的無人機和無人車用其他顏色表示。從圖3中可以看出，2個無人機分組維持定高搜索前進，無人車分組沿地面搜索前進，無人機分組與無人車分組之間形成空地協同搜索態(tài)勢。圖4給出了異構多智能體系統(tǒng)在慣性空間各軸分量的分組編隊跟蹤誤差，定義為

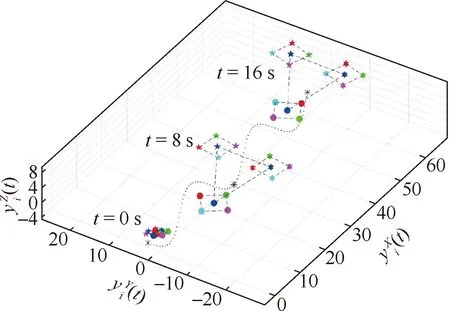
圖3 異構多智能體系統(tǒng)的搜索軌跡與各智能體部分時刻的位置信息Fig.3 Trajectory and position at certain time of heterogeneous multi-agent systems

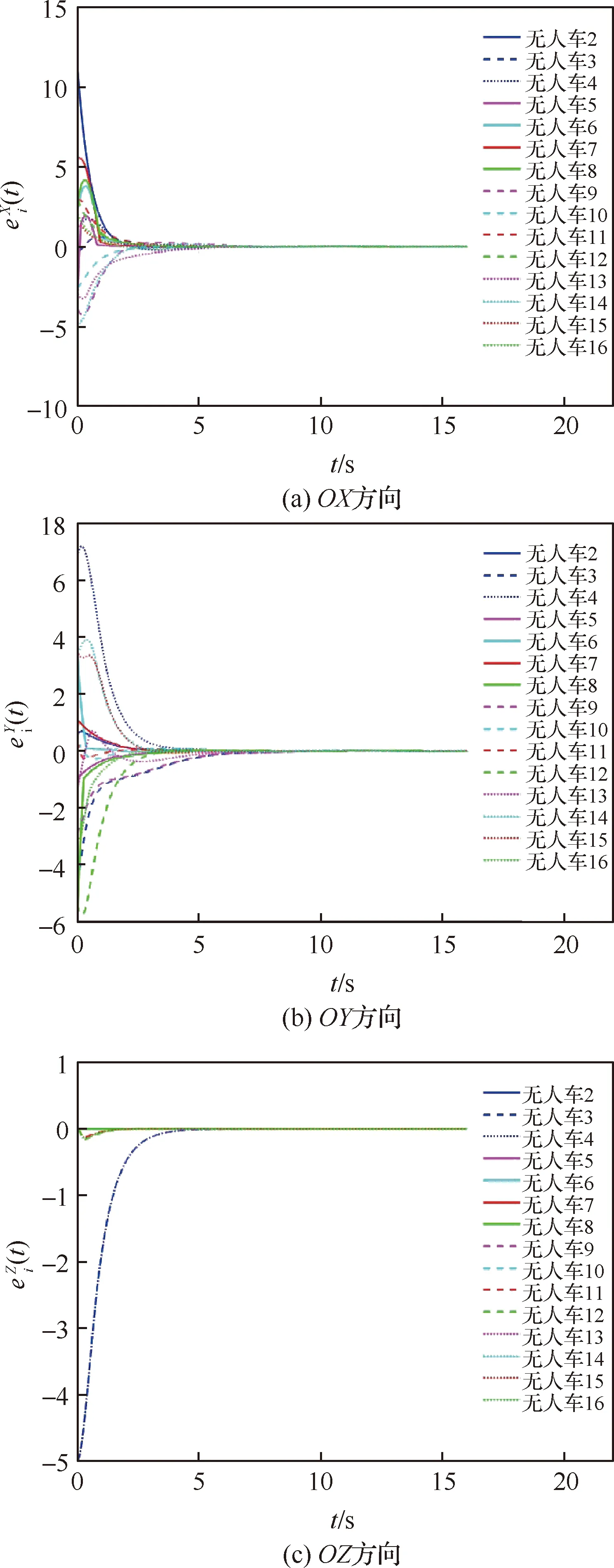
圖4 異構多智能體系統(tǒng)在慣性空間各分量的分組輸出時變編隊跟蹤誤差Fig.4 Tracking errors of time-varying output group formation of heterogeneous multi-agent systems in inertial space

ei(t)

從圖4中可以看出，編隊跟蹤誤差在慣性空間OX、OY、OZ軸方向上的分量大約于6 s后全部收斂到0。因此仿真結果驗證了本文所研究的方法能夠使異構多智能體系統(tǒng)實現分組輸出時變編隊跟蹤控制。

4 結 論

本文研究了高階異構多智能體系統(tǒng)在有向拓撲條件下的分組輸出時變編隊跟蹤控制問題。在集群系統(tǒng)中智能體的動力學模型完全不同的情況下，基于鄰居間的相對信息、觀測器理論和滑模控制理論，分別設計了針對分組領導者和跟隨者的控制協議。通過理論證明和仿真驗證結果表明，上述控制協議能夠使異構集群系統(tǒng)實現分組時變編隊跟蹤控制，因此本文給出的方法具有良好的理論價值和工程應用價值。