基于后緣襟翼偏轉的大型客機變彎度技術減阻收益

何萌，楊體浩，白俊強，楊一雄

1. 西北工業大學 航空學院，西安 710072 2. 西北工業大學 無人系統技術研究院，西安 710072

隨著人們對綠色生活環境關注度的增加以及燃油價格的不斷上漲，未來民航客機的經濟性和環保性越來越重要[1]。機翼后緣變彎度的設計增強了機翼適應各種飛行條件的能力,使工程師能在各工況下設計機翼不同的后緣偏角以改善其氣動性能,而不是一系列飛行條件下的氣動性能之間的折衷，是一種有效的減小燃油消耗的技術。

Boeing和NASA共同開展了“可變彎度后緣襟翼”(Variable Camber Continuous Trailing Edge Flap，VCCTEF)項目研究[2-3]，探索了變彎度技術用于未來質量更輕、機翼柔性更大的飛行器的性能優勢，比如提高巡航效率、擴寬抖振邊界、增加機動性等。Boeing757的原型機GTM(Generic Transport Model)構型上使用此項技術，有效減小了其巡航阻力[4-5]。Boeing787也采用了機翼后緣變彎度設計，所減少的巡航阻力相當于節省340～450 kg(750～1 000 lb)的重量[6]。

變彎度的結構設計[7-9]目前具有較高的技術儲備，比如FlexSys FlexFoil裝置[10-11]改變襟翼偏角時，控制表面仍能呈現出平滑和連續的過度。國內外學者對機翼后緣變彎度技術在氣動設計中的收益也已經開展了廣泛的研究。Molinari等[12-13]和Lee等[14]使用低精度氣動模型研究了后緣連續變彎的優點；Lyu和Martins[15-16]使用高精度的伴隨求解器對CRM機翼后緣連續變彎度技術的收益進行研究，對407個可能的飛行狀態進行后緣變彎度的優化，生成一個優化構型的數據庫，分析了后緣變彎度技術對燃油消耗的減小量，但是沒有考慮到配平阻力對減阻收益的影響。Burdette等[17-18]使用氣動結構求解器對后緣變彎度的收益進行了研究，結果表明，可變彎的機翼有1.02%的燃油收益，考慮結構變形的影響，燃油可減小1.72%。梁煜[19]和陳錢[20]等以翼型為例，研究了翼型后緣變彎度對氣動性能與壓力分布的影響。郭同彪等[21-22]研究了后緣連續變彎度對跨聲速翼型氣動特性的影響，以及針對民用客機機翼-機身-平尾構型開展了后緣連續變彎度機翼氣動優化設計。

之前的工作主要針對二維翼型以及機翼全翼展連續變彎對氣動特性的影響研究，全翼展連續變彎是機翼成型各控制剖面后緣均可變彎，設計變量較多，且對機翼變形材料要求較高，在規律研究上具有指導意義。但是針對大型客機，連續變彎技術的技術成熟度和可靠性有待進一步提高，目前尚無法在工程實際中得到應用。波音公司為787飛機測試和開發了一種后緣可變彎度(TEVC)系統，在巡航時通過操縱后緣內外襟翼以0.5°為增量進行偏轉[6]。本文考慮了工程實際約束的影響，只對內外襟翼進行變彎偏轉(具有兩個設計變量)，對寬體客機進行了減阻收益評估。在考慮配平阻力的影響下探究了變彎度技術對阻力發散和抖振邊界設計要求的拓展能力，以及變彎度技術在非設計點的減阻收益；內外襟翼偏角不同可能會使氣動性能的改善效果更好，但會導致機翼后緣變彎機構更加復雜，因此對比了襟翼同偏和差偏在氣動上的減阻收益；分析了在不同非設計點機翼后緣變彎度技術的壓力分布變化規律、載荷分布變化規律，并進一步采用遠場阻力分解方法探究了變彎度技術的減阻機理。

1 三維機翼后緣變彎度建模

變彎度時使用如圖1 所示的襟翼平面形狀，具有兩個設計變量，分別為內襟翼偏角和外襟翼偏角。采用定軸偏轉的方式偏轉襟翼，偏轉前后的效果對比如圖2 所示，可以看到，變彎度后的翼面依然保持著連續、光滑的特征。同時由于機構的行程和精度限制，要求襟翼以0.5°的卡位運行，且最大偏角不超過2°，規定襟翼下偏為正，上偏為負。平尾也作為一個額外的自由度參與考慮，即通過平尾安定面的偏轉來配平俯仰力矩,使變彎度構型的俯仰力矩與基礎構型一致。

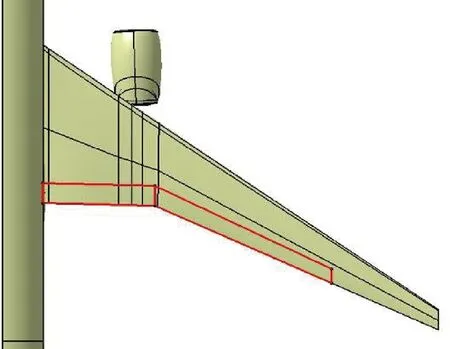
圖1 襟翼平面形狀Fig.1 Flap plane shape

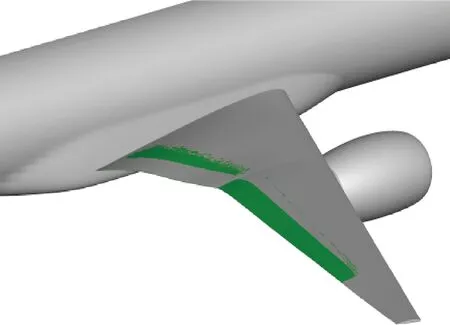
圖2 變彎度偏轉效果Fig.2 Variable camber deflection effect

由于掛架只對局部的流場產生影響，對整體氣動特性影響不大[23-24]，且為了減小網格量和減小流場的復雜性，建模時沒有考慮掛架的影響[25]。

2 數值求解方法

本文使用雷諾-平均Navier-Stokes (RANS)方程求解器進行定常求解。全湍流計算，使用的湍流模型為剪切應力輸運(SST)湍流模型。選取CRM翼身組合體構型[26]對求解器精度進行校驗，網格量為1 725萬，計算狀態為:馬赫數Ma=0.85, 雷諾數Re=5×106, 升力系數CL=0.519。

4個控制剖面的壓力系數Cp分布計算結果與試驗數據的對比如圖3 所示，求解器計算得到的壓力分布形態與試驗值吻合良好，尤其是下表面貼合較好。對比結果表明，本文采用的求解器具有可滿足工程應用需求的計算精度和可靠性。寬體構型計算時采用多塊結構網格，網格拓撲如圖4 所示。

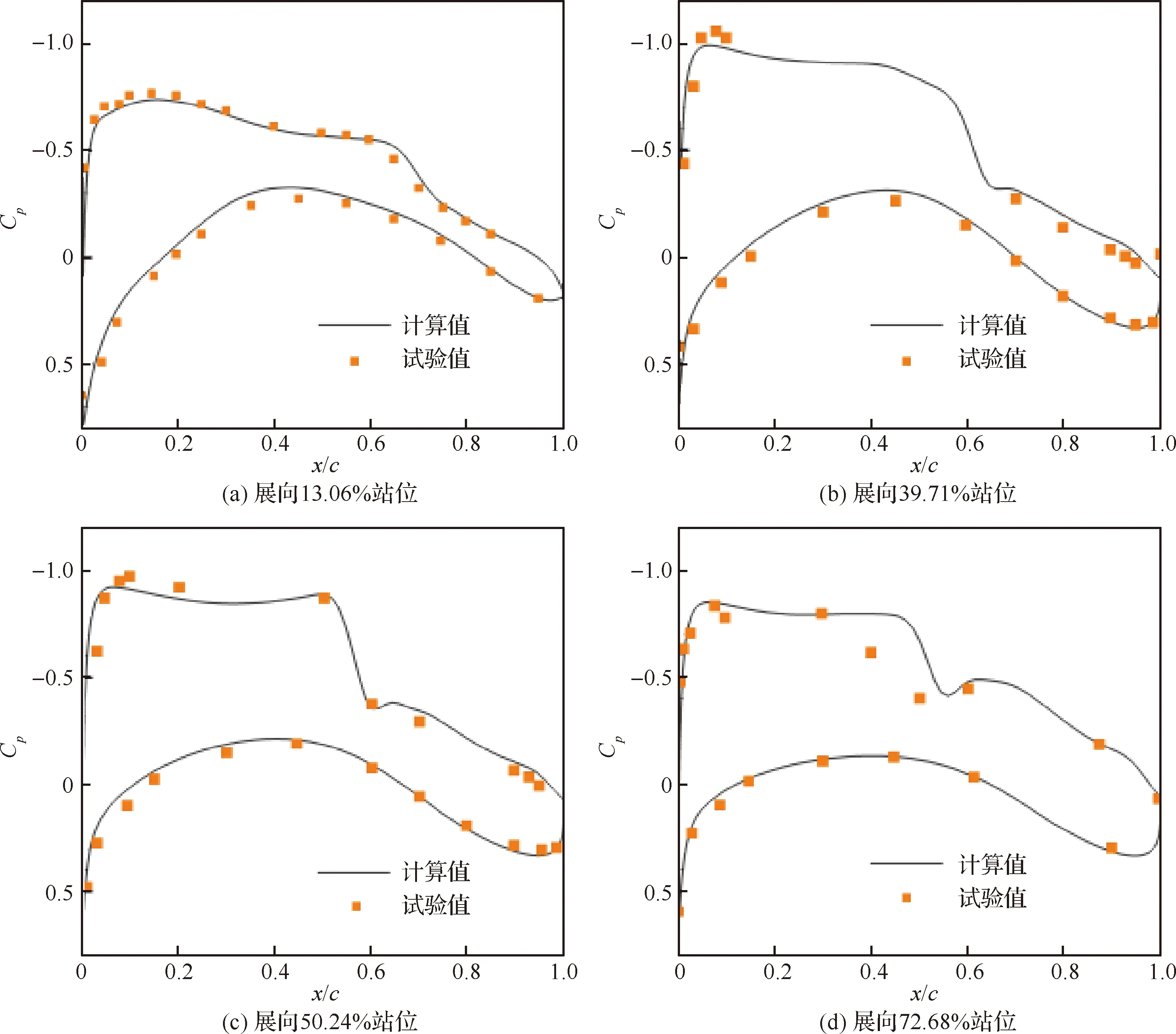
圖3 CRM構型計算結果與試驗數據對比Fig.3 Comparison of CRM configuration calculation results with experimental data

圖4 計算網格拓撲Fig.4 Grid topology

為了明確網格量對計算結果的影響，本文計算了2 000萬、3 000萬和4 300萬網格量下阻力系數的數值，計算結果如表1 所示。使用2 000萬網格計算時，相較于3 000萬的網格量，計算出來的阻力值增加7.5 counts(1 count=0.000 1)，使用4 300萬的網格相較于3 000萬的網格，阻力值只增加了約2 counts。從工程應用研究角度，可認為3 000萬網格與4 300萬網格具有相當的計算精度水平。考慮到本文計算量大，為了兼顧計算時間和計算精度，最終采用3 000萬的網格量用于變彎度技術減阻收益的評估。

表1 基礎構型不同網格量計算結果

3 基礎構型氣動性能

表2給出了未考慮襟翼變彎的基礎構型氣動特性，設計馬赫數Ma=0.85，設計升力系數CL=0.48，雷諾數Re=4.7×107。巡航設計點力矩基本配平，巡航攻角為2.48°，阻力系數為230.98 counts，升阻比為20.78。馬赫數0.87與馬赫數0.85的阻力差量為17.53 counts，阻力發散特性較好。圖5 為馬赫數0.85機翼表面壓力分布及流線圖。

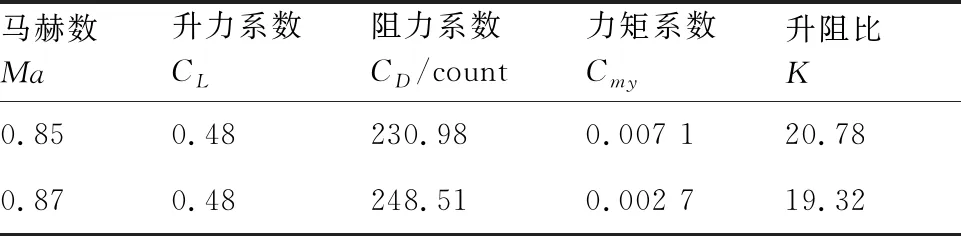
表2 基礎構型氣動性能Table 2 Aerodynamic performance of original configuration

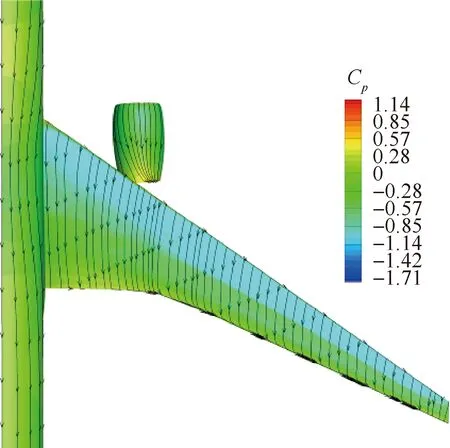
圖5 馬赫數0.85機翼表面壓力系數分布及流線圖Fig.5 Pressure coefficient distribution and surface streamline of wing (Ma =0.85)

4 采用變彎度技術的狀態選取

變彎度技術能夠在巡航過程中通過改變后緣偏角，在非設計點狀態下獲得減阻收益，從而降低整個巡航段的平均阻力。因此，本文選取的變彎度技術減阻收益評估狀態包括以下3類：

1) 隨著飛行過程中燃油不斷消耗，飛機的升力系數也會隨時間發生變化[17,27]。故選取了升力系數變化10%和20%的非設計點，即小升力系數點(CL=0.432和CL=0.384)和大升力系數點(CL=0.528和CL=0.576)。在此基礎上，進一步分析整個升力系數變化范圍內的減阻規律。

2) 受航空管制以及變高度巡航策略等因素的影響，民用客機難以在整個巡航階段內都以一個固定的設計馬赫數進行巡航，其巡航馬赫數往往會在設計馬赫數附近小幅變化[17]。故選取了馬赫數偏小點(Ma=0.83，CL=0.48)和阻力發散點(Ma=0.87，CL=0.48)進行變彎度技術的減阻收益研究。

3) 研究變彎度技術對升力系數增加所引起的高速抖振特性的影響。對于大型民用客機，設計規范要求其具有1.3 g的抖振裕量，故重點研究了變彎度技術對抖振點(Ma=0.85，CL=0.624)氣動特性的改善作用。

最終，選取的計算狀態的分布如圖6 所示。

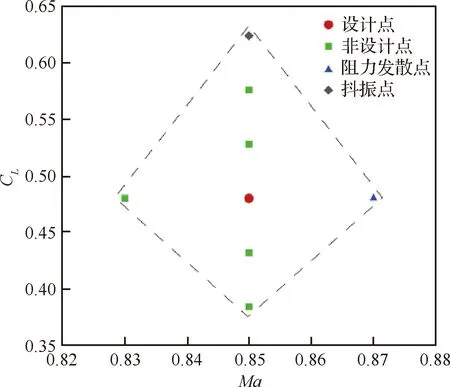
圖6 變彎度設計的計算狀態分布Fig.6 Calculation condition distribution of variable camber design

5 變升力系數狀態后緣變彎技術減阻收益

5.1 小升力系數下的減阻收益

對內外襟翼的可能偏角進行遍歷計算，表3給出了CL=0.384狀態下基礎構型、不考慮力矩配平阻力的最佳襟翼偏角構型、考慮配平阻力的最佳襟翼同偏構型和最佳襟翼差動偏轉構型結果。襟翼同偏表示內、外襟翼的偏角一致，差動偏轉表示內、外襟翼的偏角不一致。

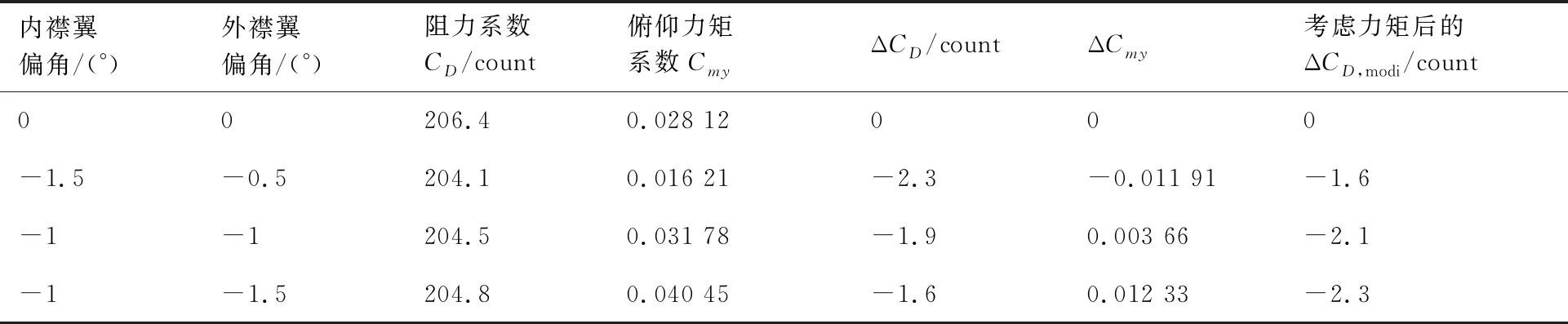
表3 基礎構型與最優襟翼偏角構型氣動力系數(CL=0.384)Table 3 Aerodynamic coefficients of original configuration and optimal flap declination configuration (CL=0.384)

圖7給出了CL=0.384時的計算結果，Inner表示內襟翼偏角，Outer表示外襟翼偏角，可以看到小升力系數時襟翼上偏有助于阻力減小，內襟翼上偏，外襟翼下偏，造成低頭力矩增加，而襟翼同偏對力矩系數的影響不大。不考慮力矩配平阻力的最優襟翼偏角為內襟翼-1.5°，外襟翼-0.5°，減阻2.3 counts；考慮配平阻力后僅減阻1.6 counts；考慮配平阻力下最佳同偏襟翼偏角為-1°，減阻2.1 counts，最佳差動偏轉襟翼偏角為內襟翼-1°，外襟翼-1.5°，減阻2.3 counts。

表4和圖8給出了CL=0.432的計算結果，不考慮力矩配平阻力的最佳襟翼偏角為內襟翼-1.0°，外襟翼-0.5°，減阻1.4 counts;考慮配平阻力后僅減阻1.2 counts；考慮配平阻力下最佳襟翼偏角為內襟翼-0.5°，外襟翼-0.5°，減阻1.4 counts。可見，是否考慮力矩配平對最佳襟翼偏角和減阻量有較大影響，在進行變彎度減阻收益研究時有必要考慮配平阻力的影響。

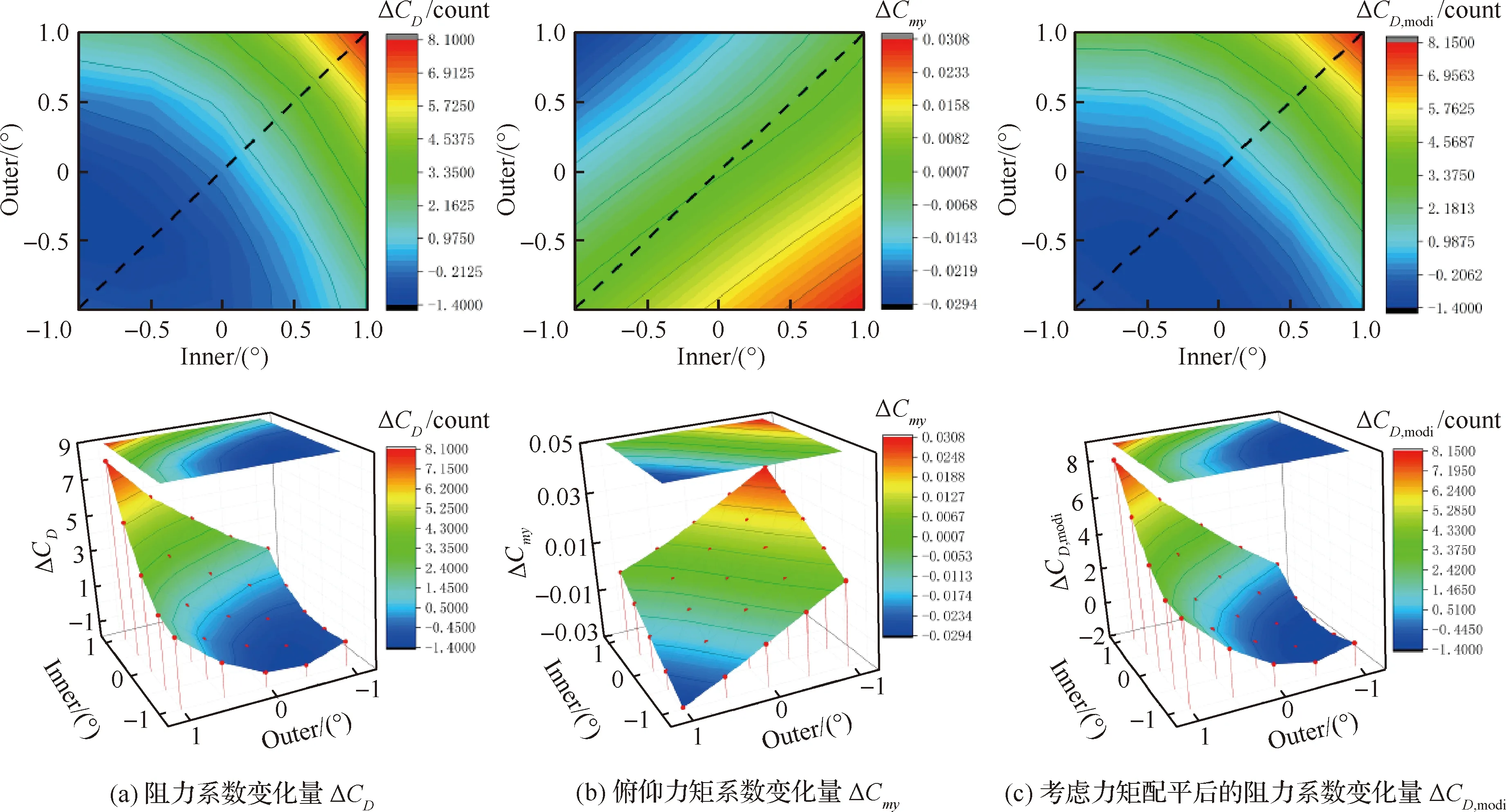
圖8 不同內外襟翼偏角下的氣動阻力以及俯仰力矩系數變化云圖(CL=0.432)Fig.8 Contour of aerodynamic drag and pitching moment coefficient at different inner and outer flaps (CL=0.432)

表4 基礎構型與最優襟翼偏角構型氣動力系數(CL=0.432)Table 4 Aerodynamic coefficients of original configuration and optimal flap declination configuration (CL=0.432)

圖9、圖10 給出了變彎前后機翼上激波強度對比、環量分布對比及剖面壓力系數Cp對比，Original 表示基礎構型，TEVC表示變彎構型(襟翼同偏最優結果)。對于小升力系數的計算工況，內外襟翼均上偏使得機翼后緣卸載，巡航攻角增大，引起激波位置后移，載荷前移。機翼載荷前移導致抬頭力矩增加。同時機翼中后緣部分載荷減小，使壓力恢復平緩，激波強度減小。通過機翼展向環量分布對比可以看出，機翼襟翼的同時上偏使載荷外移，更加貼近橢圓形環量分布。

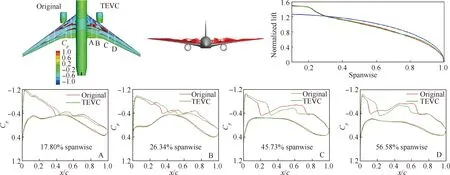
圖9 變彎前后對比(內襟翼-1°，外襟翼-1°，CL=0.384)Fig.9 Comparison of initial and flap deflection configurations (inner flap -1°, outer flap -1°, CL=0.384)

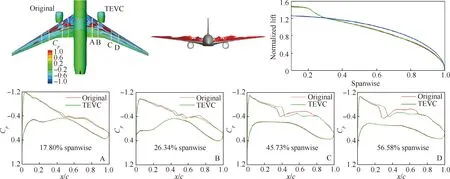
圖10 變彎前后對比(內襟翼-0.5°，外襟翼-0.5°，CL=0.432)Fig.10 Comparison of initial and flap deflection configurations (Inner flap -0.5°, Outer flap -0.5°, CL=0.432)

5.2 大升力系數下減阻收益

表5和圖11 給出了CL=0.528的計算結果，從圖11 可以看出，大升力系數下，襟翼下偏有助于阻力減小，襟翼偏角變化對力矩系數的影響與小升力系數時基本一致。不考慮力矩配平阻力的最佳襟翼偏角為內襟翼0.5°，外襟翼1.0°，減阻5.5 counts;考慮配平阻力后僅減阻4.2 counts；考慮配平阻力的最佳同偏襟翼偏角為1°，減阻5.0 counts，最佳差動偏轉襟翼偏角為內襟翼1.5°，外襟翼0.5°，減阻5.7 counts。

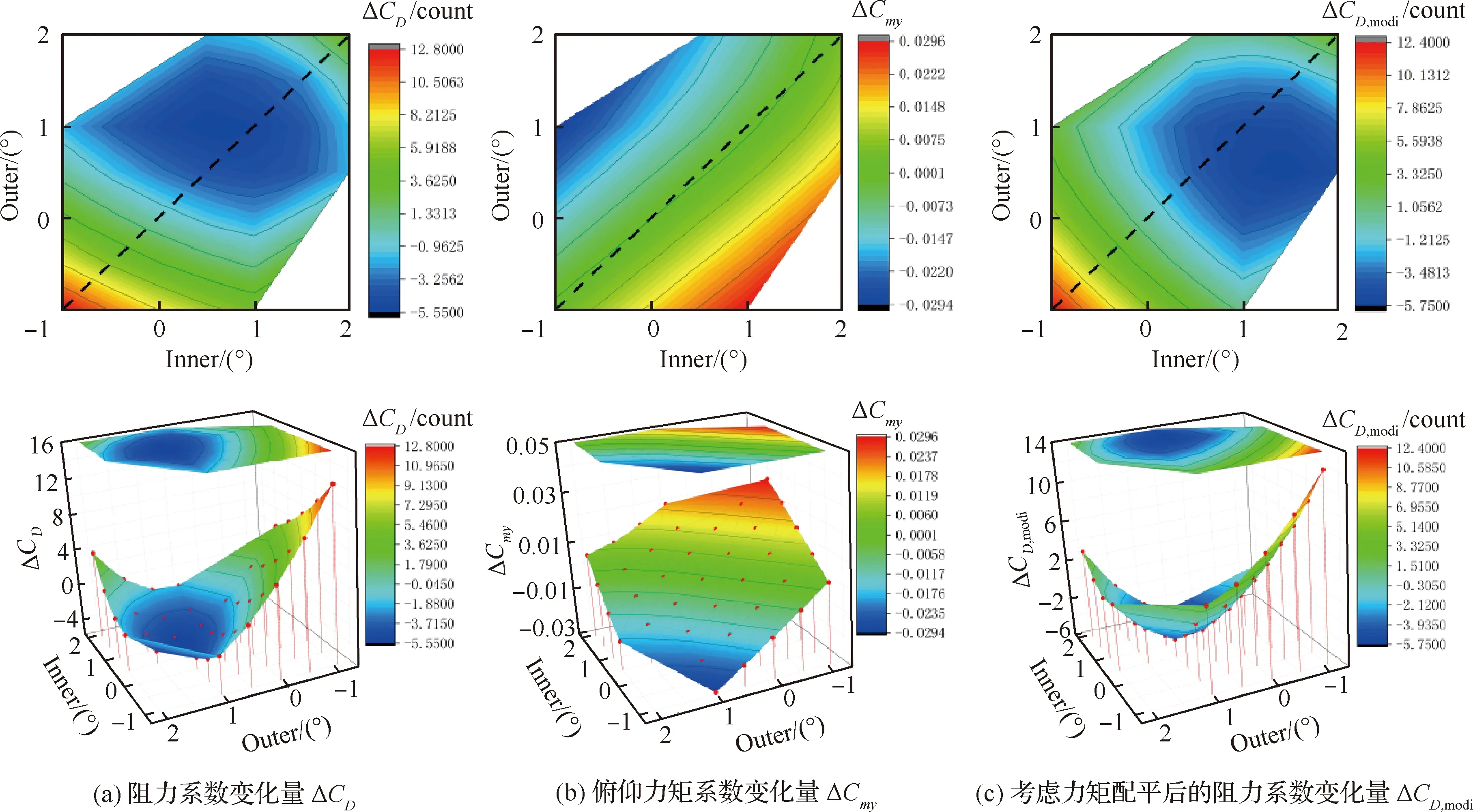
圖11 不同內外襟翼偏角下的氣動阻力以及俯仰力矩系數變化云圖(CL=0.528)Fig.11 Contour of aerodynamic drag and pitching moment coefficient at different inner and outer flaps (CL=0.528)

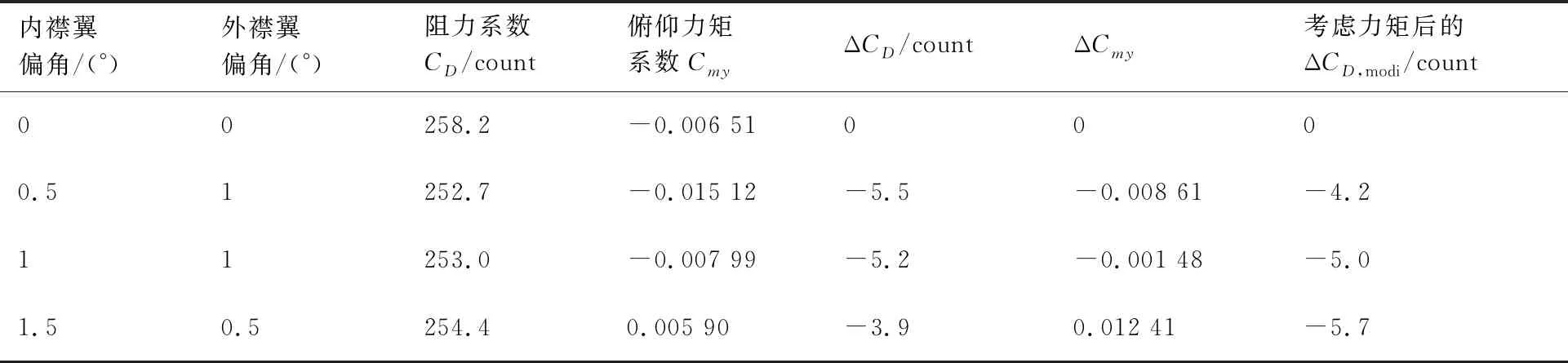
表5 基礎構型與最優襟翼偏角構型氣動力系數(CL=0.528)Table 5 Aerodynamic coefficients of original configuration and optimal flap declination configuration (CL=0.528)

表6和圖12 給出了CL=0.576的計算結果，不考慮力矩配平阻力的最佳襟翼偏角為內襟翼1.0°，外襟翼1.5°，減阻14.0 counts；考慮配平阻力后僅減阻12.2 counts；考慮配平阻力的最佳同偏襟翼偏角為1.5°，減阻12.9 counts，最佳差動偏轉襟翼偏角為內襟翼2.0°，外襟翼1.0°，減阻13.5 counts。大升力系數下，變彎度技術具有較為明顯的氣動性能的改善。配平阻力依然對結果有較大影響，在進行變彎度減阻收益研究時有必要考慮配平阻力的影響。

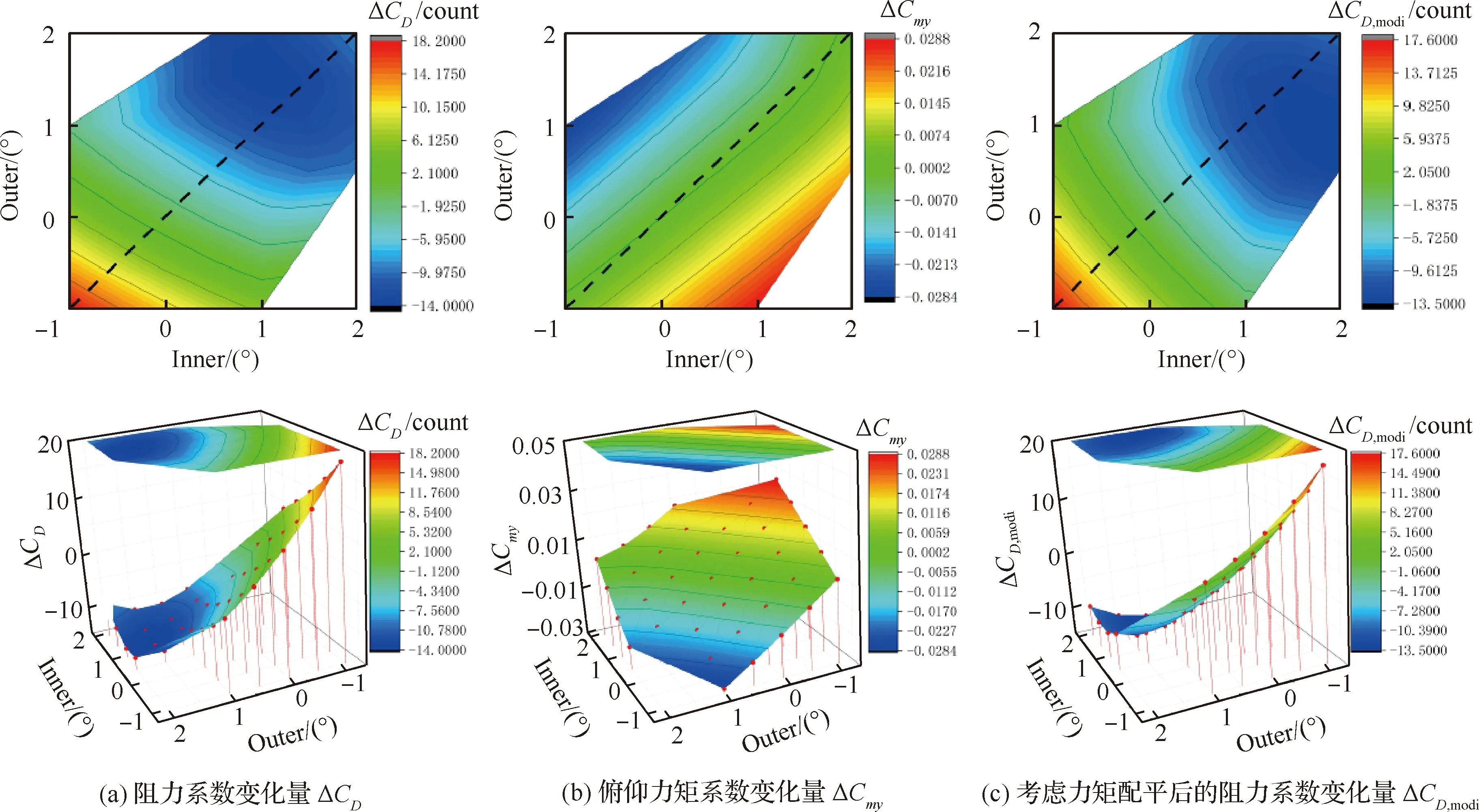
圖12 不同內外襟翼偏角下的氣動阻力以及俯仰力矩系數變化云圖(CL=0.576)Fig.12 Contour of aerodynamic drag and pitching moment coefficient at different inner and outer flaps (CL=0.576)

表6 基礎構型與最優襟翼偏角構型氣動力系數(CL=0.576)Table 6 Aerodynamic coefficients of original configuration and optimal flap declination configuration (CL=0.576)

圖13和圖14 給出了變彎前后機翼上激波強度對比、環量分布對比及剖面壓力系數Cp對比。大升力系數下，內外襟翼均下偏使得機翼后緣加載，上翼面的壓力分布會變得飽滿，壓力恢復平緩，激波強度降低，波阻減小。通過機翼展向環量分布對比可以看出，機翼襟翼的同時下偏使載荷內移，環量分布更加偏離橢圓形環量分布。

6 變馬赫數狀態減阻收益

6.1 馬赫數偏小(Ma=0.83)時的減阻收益

從表7 和圖15可看出在不考慮力矩配平阻力的影響下，內襟翼偏轉-1°，外襟翼偏轉0.5°，減阻0.5 counts，但此偏轉條件下，低頭力矩增加，考慮配平阻力后，阻力增加0.5 counts。

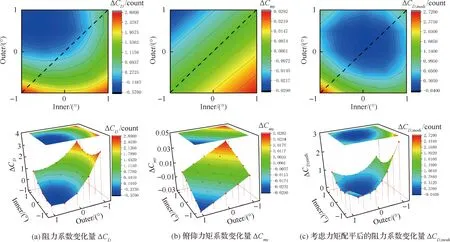
圖15 不同內外襟翼偏角下的氣動阻力以及俯仰力矩系數變化云圖(Ma=0.83)Fig.15 Contour of aerodynamic drag and pitching moment coefficient at different inner and outer flaps (Ma=0.83)

表7 基礎構型與最優襟翼偏角構型氣動力系數(Ma=0.83)Table 7 Aerodynamic coefficients of original configuration and optimal flap declination configuration (Ma=0.83)

對于馬赫數偏小的非設計點，首先由于激波位置在變彎區域之前且距離太遠，變彎控制的效果較弱,沒有較為明顯的減阻效果。其次最優偏角為內襟翼上偏，外襟翼下偏，導致機翼載荷外移，低頭力矩增加，造成配平阻力增加。因此考慮力矩配平的影響之后，變彎度技術對馬赫數偏小的非設計點沒有帶來氣動特性的改善。

6.2 阻力發散點(Ma=0.87)的減阻收益

從表8 和圖16可看出在不考慮力矩配平阻力的影響下，內襟翼偏轉-1°，外襟翼偏轉0.5°，減阻1.4 counts，但此偏轉條件下，低頭力矩增加，考慮配平阻力后，阻力增加2.4 counts。

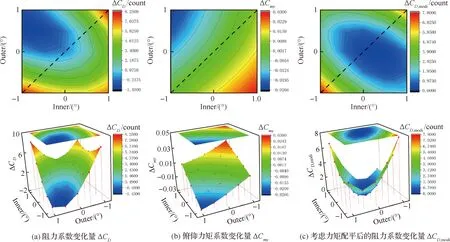
圖16 不同內外襟翼偏角下的氣動阻力以及俯仰力矩系數變化云圖(Ma=0.87)Fig.16 Contour of aerodynamic drag and pitching moment coefficient at different inner and outer flaps (Ma=0.87)

對于阻力發散點，首先由于激波位置靠后，以至于在變彎度過渡區之后，變彎控制的效果也很弱。其次考慮力矩的影響之后，配平阻力的增加使變彎度技術對阻力發散點也沒有帶來氣動特性的改善。

在不同的馬赫數下，不論是馬赫數增大還是減小，內襟翼上偏、外襟翼下偏導致機翼載荷外移，低頭力矩增加，考慮力矩系數后，變彎度的減阻收益均為0。

7 變彎度技術對抖振特性的改善作用

表9和圖17 給出了CL=0.624抖振點的計算結果，考慮力矩配平阻力時，最佳同偏襟翼偏角為1.5°，減阻18.8 counts，最佳差動偏轉襟翼偏角為內襟翼2.0°，外襟翼1.0°，減阻21.2 counts。

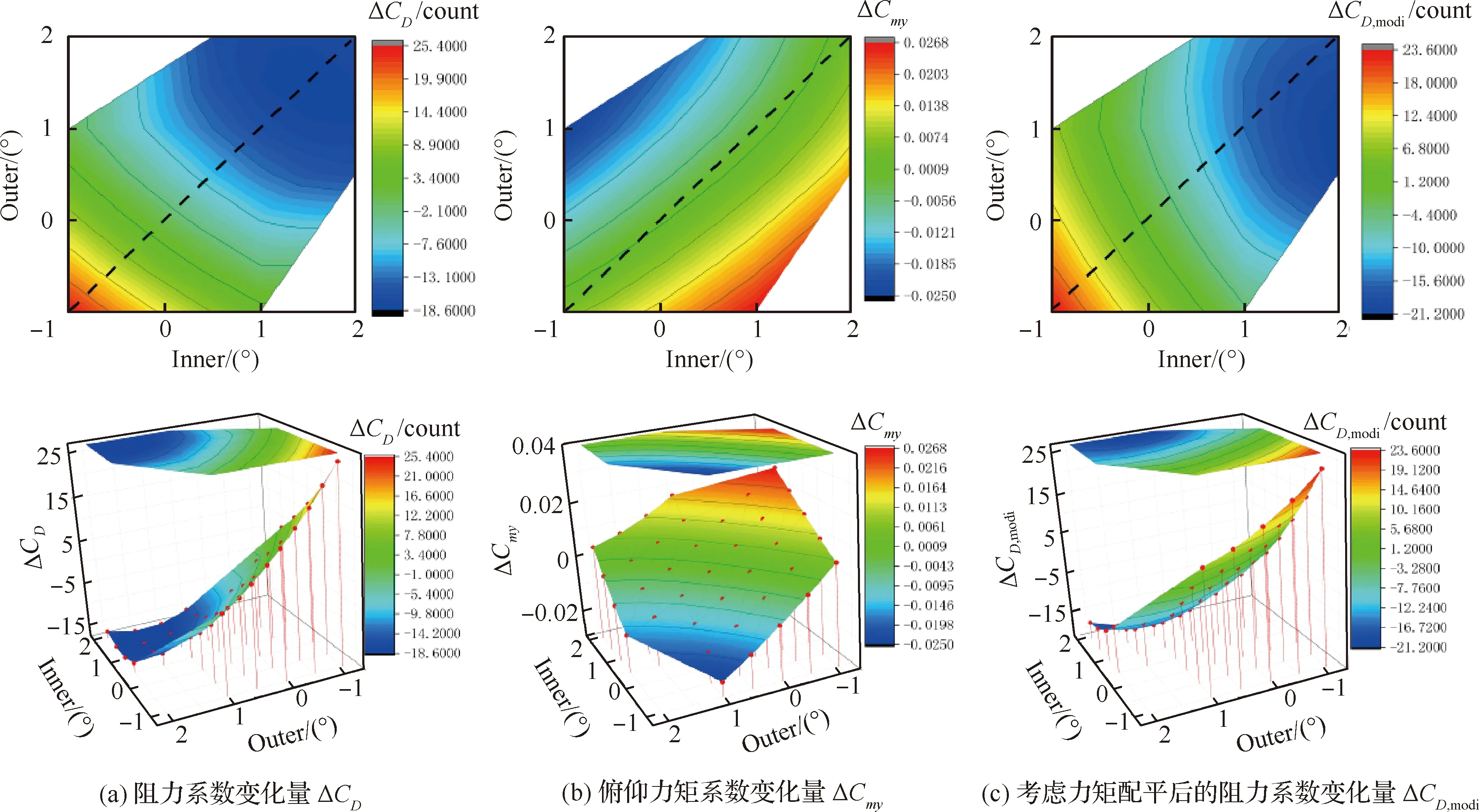
圖17 不同內外襟翼偏角下的氣動阻力以及俯仰力矩系數變化云圖(CL=0.624)Fig.17 Contour of aerodynamic drag and pitching moment coefficient at different inner and outer flaps (CL=0.624)

表9 基礎構型與最優襟翼偏角構型氣動力系數(CL=0.624)Table 9 Aerodynamic coefficients of original configuration and optimal flap declination configuration (CL=0.624)

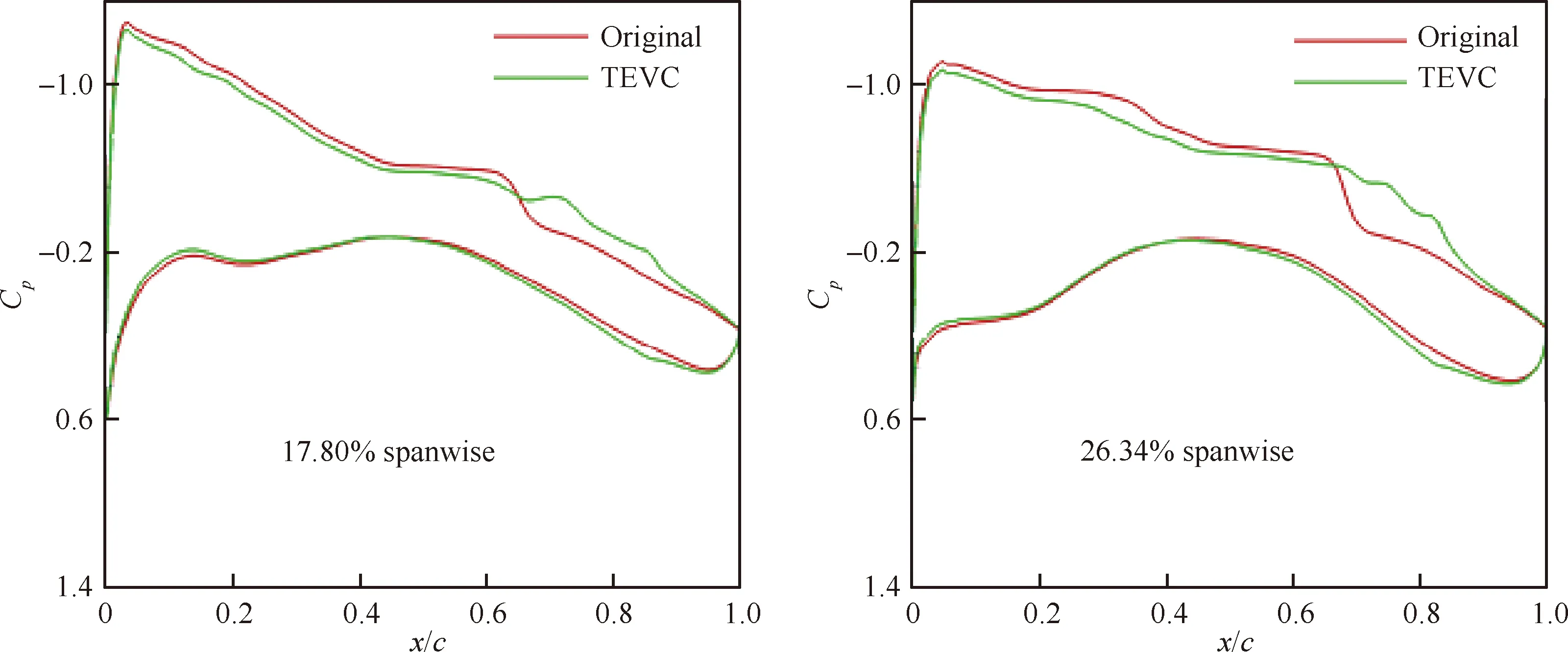
圖18給出了抖振點襟翼同偏變彎前后機翼剖面壓力系數Cp對比。內外襟翼下偏，機翼后緣載荷增加。內翼段通過襟翼下偏，壓力恢復平緩，呈無激波形態，中外翼段通過外襟翼下偏，激波位置后移，激波強度減小。

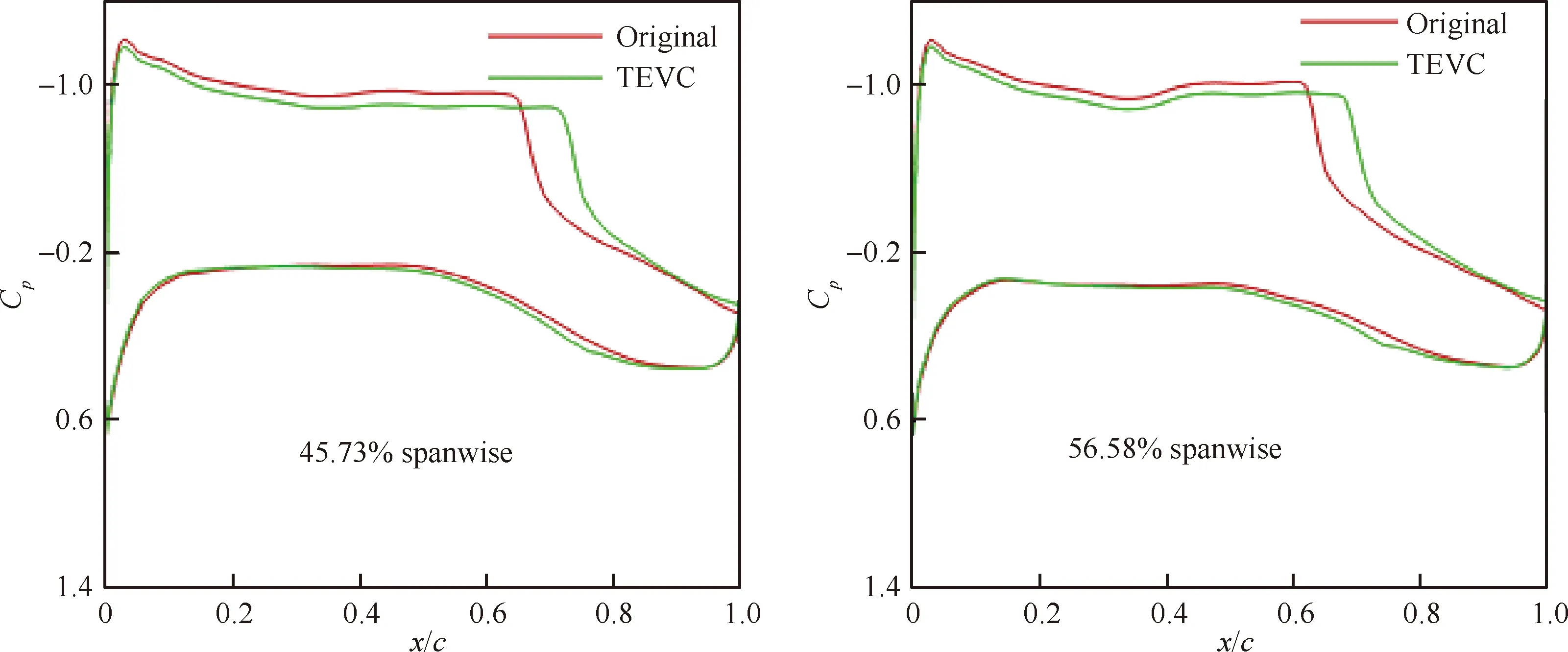
圖18 襟翼同偏變彎前后機翼剖面壓力系數對比(內襟翼1.5°，外襟翼1.5°，CL=0.624)Fig.18 Comparison of wing section pressure coefficient of original and flap deflection configurations (Inner flap 1.5°, Outer flap 1.5°, CL=0.624)

抖振是激波附面層干擾引起分離流產生的非定常氣動力引起的振動現象[28]。圖19 為變彎前和變彎后的抖振特性對比，給出了一系列升力系數下的機翼上表面壓力云圖與極限流線。變彎前構型在CL=0.594和CL=0.604下的分離區大小分別接近于變彎后構型在CL=0.624和CL=0.634下的分離區大小，結果表明變彎度可改善抖振特性。變彎度通過調整載荷分布，明顯降低中外翼激波強度，減緩了激波誘導分離的趨勢。

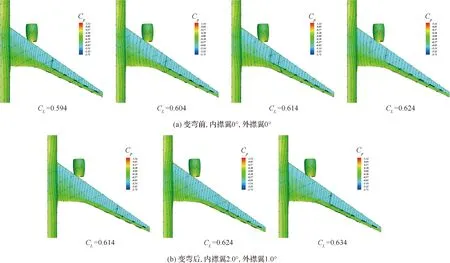
圖19 變彎前和變彎后抖振特性對比Fig.19 Comparison of buffeting characteristics before and after flap deflection

8 變彎度技術非設計點減阻機理分析

圖20給出了不同升力系數下變彎度的減阻情況(考慮力矩系數配平后),其中藍線和綠線分別給出了同偏與差動偏轉下的結果。可以看到，偏離設計點升力系數越遠，變彎度獲得的減阻收益越大，且大升力系數時的收益要大于小升力系數時的收益。對比同偏和差動偏轉，兩者減阻量隨升力系數變化的變化趨勢基本一致，差動偏轉的收益略高于同偏的收益。

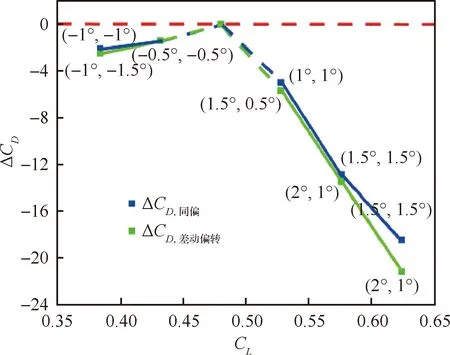
圖20 不同升力系數下變彎度的減阻量(考慮力矩系數配平后)Fig.20 Drag reduction of variable camber under different lift coefficients (considering trimming moment coefficient)

進一步采用遠場阻力分解方法[29-30]探究了變彎度技術的減阻來源，遠場阻力分解方法是基于線性動量定理關系進行阻力計算，將阻力按照產生的機制分為黏性阻力、激波阻力、誘導阻力和偽阻力。

圖21給出了不同升力系數下變彎前后激波阻力值對比，小升力系數狀態下波阻減小量不足1 count。大升力系數狀態下，波阻有明顯的減小。波阻的減小主要是因為后緣襟翼變彎度技術會調整載荷分布，改變激波位置和強度。

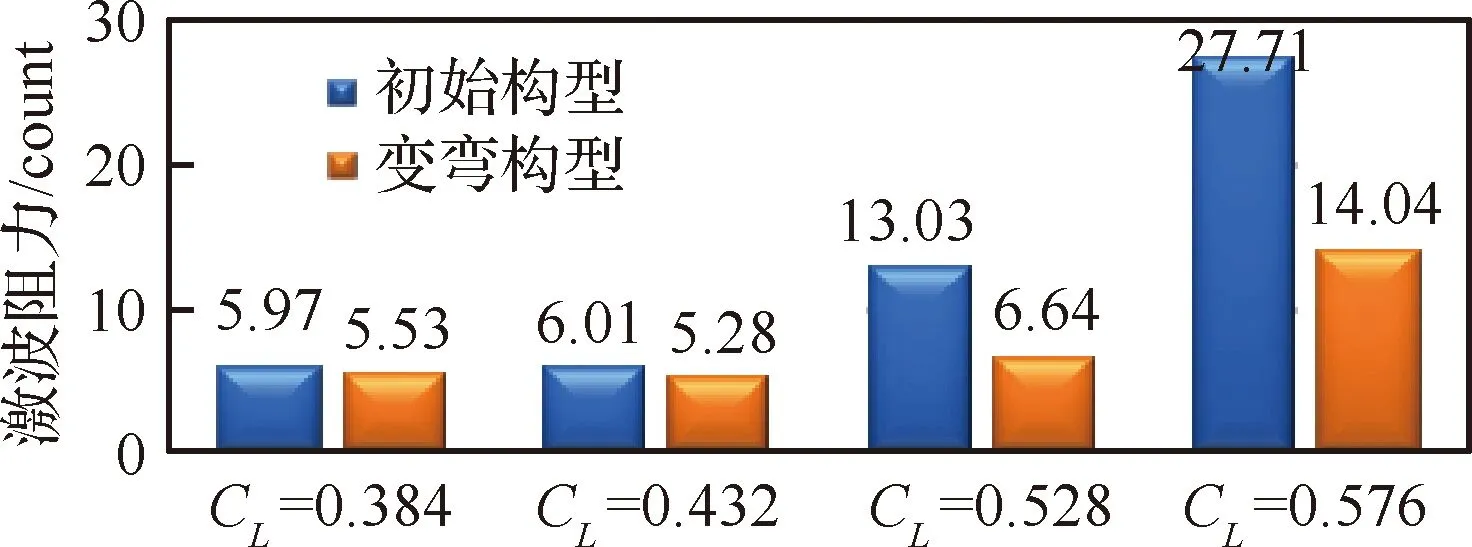
圖21 變彎前后激波阻力對比Fig.21 Comparison of shock drag of original and flap deflection configurations

圖22給出了不同升力系數下變彎前后誘導阻力值對比。在不同升力系數下，誘導阻力值沒有明顯改善。從之前的環量分布對比可以看出，在大升力系數時，載荷內移，更加偏離橢圓形環量分布，導致誘導阻力略微增加。

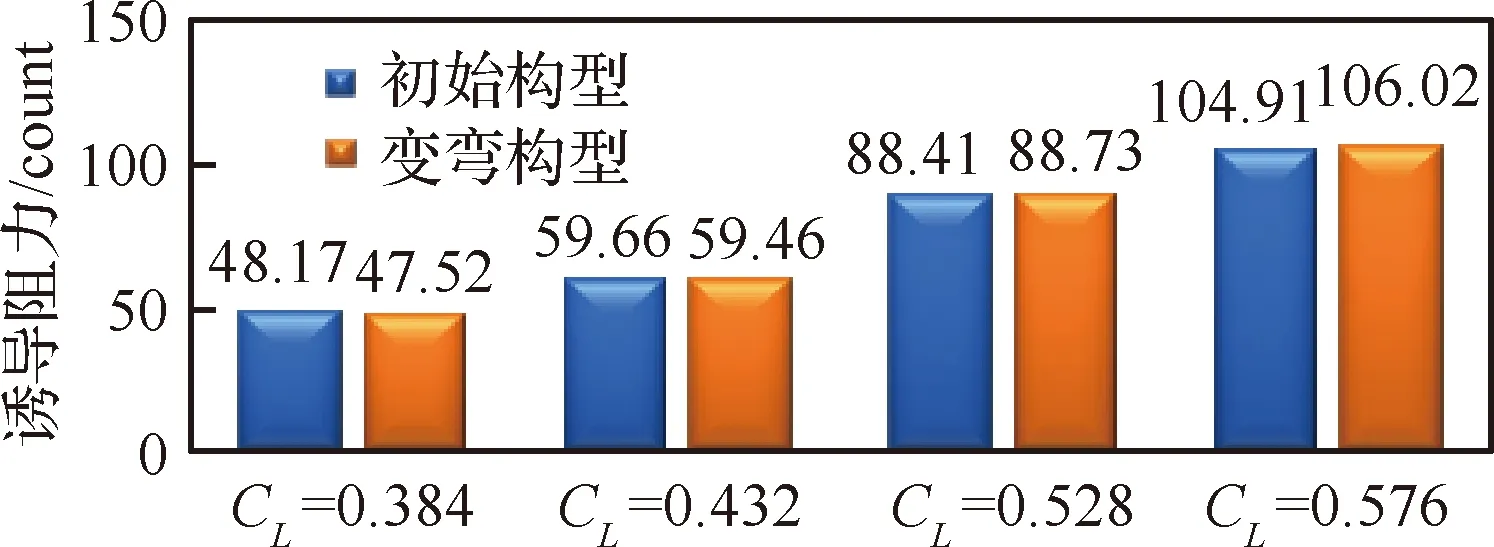
圖22 變彎前后誘導阻力對比Fig.22 Comparison of induced drag of original and flap deflection configurations

9 結 論

1) 變彎度引起全機俯仰力矩變化帶來的配平阻力，對變彎度減阻收益影響明顯，考慮配平阻力損失是進行變彎度機翼設計的關鍵。

2) 在整個巡航升力系數范圍內的非設計點，變彎度均能取得一定減阻收益，大巡航升力系數下減阻收益更大。不同巡航升力系數下變彎度減阻機理存在明顯差異。小巡航升力系數下誘導阻力以及激波阻力都得到不同程度的減小。大巡航升力系數下以適當增大誘導阻力的方式，顯著削弱激波阻力。

3) 變彎度通過將機翼載荷內移，削弱激波強度，減小激波誘導的附面層分離，拓展抖振邊界裕度。

4) 變彎度無法改善阻力發散點和阻力蠕增特性。

5) 對比差動偏轉和同偏，兩者的減阻收益隨升力系數的變化趨勢一致，但在某些情況下，差動偏轉減阻收益更明顯。