基于單顆粒模型的航發葉片砂帶磨削微觀仿生鋸齒狀表面形成及實驗

肖貴堅，賀毅，黃云，李偉，李泉

重慶大學 機械傳動國家重點實驗室，重慶 400044

由鯊魚皮衍生出來的仿生表面結構在航空發動機葉片、整體葉盤等轉動構件表面的形成對于提高其減阻、降噪、抗疲勞等服役性能具有重要的影響；同時鈦合金材料具有比重小、比強度高、韌性高、疲勞裂紋擴展速率低、耐腐蝕性好等優點[1]，作為輕質材料被廣泛應用于上述轉動構件的設計中，其加工后的型面精度和表面紋路、粗糙度、顯微硬度、殘余應力、亞表層組織等表面完整性特征對上述鈦合金轉動構件的疲勞壽命、氣流動力性和使用性能影響巨大，因此研究鈦合金仿生表面的加工方法具有重要意義。

由于葉片具有復雜的型面和較弱的剛度，因此主要通過砂帶磨削等精密加工方法來保證葉片的最后精度。但對于砂帶磨削仿生表面的形成與砂帶單顆粒模型和砂帶多顆粒磨削方法的關系,目前尚未揭示，因而提出基于單顆粒模型的航發葉片砂帶磨削微觀仿生鋸齒狀表面形成方法及試驗。

對于鯊魚皮仿生表面的加工可分為兩種[2]，一種是直接復刻鯊魚皮的表面盾鱗結構，另一種是基于鯊魚皮表面結構衍生出來的設計制備的溝槽。對于后一種方法，針對溝槽結構具有代表性的加工方法有磨削加工技術。Xie[3-4]等利用金剛石砂輪在單晶硅上干磨出微溝槽，并且發現微溝槽的形狀與砂輪上的金剛石磨粒狀參數有關，如金剛石磨粒的前角，磨粒尖端的半徑的大小等。Denkena等[5]提出了磨削輪溝槽結構加工方法，即多輪廓磨削法。該方法在制備磨削輪的效率和工藝穩定性上具有優勢，通過這種工藝能夠很有效率地加工溝槽結構，但磨削法成形的溝槽結構較為粗糙，容易形成毛刺。Brinksmeier和Sch?nemann[6]采用金剛石微鑿切加工出了不連續的微觀結構，如微型立方體和V型溝槽；研究發現，可加工顯微結構的尺寸主要受加工相關形狀偏差的限制，增加結構尺寸對表面光潔度沒有明顯的影響；然而，大尺寸結構的加工會導致切削力的線性增加。

針對航發鈦合金葉片等零部件的表面精密磨削加工，國內外采用了磨料流[7-8]、砂帶磨削以及手工拋光等方法，對于提升葉片表面完整性具有一定的作用。砂帶磨削兼具磨削和拋光的雙重作用，其工藝靈活性高、適應性強，且其柔性磨削的特性在型面平滑過渡方面具有獨特的擬合效果[9]。鑒于上述特性，目前砂帶磨削技術已經成功應用于航發葉片的精密磨削中，成為提高其表面完整性的有效加工技術之一[10]。Eckart和Florian[11-12]以及Xu等[13]采用了機器人輔助砂帶磨削的方法進行了渦輪葉片精密加工，并通過力控的方法實現加工過程的自適應從而提高了加工效率、加工精度和葉片表面質量。張雷等[14]對航發葉片雙曲面砂帶磨削工藝、恒力磨削方法等進行了研究，提出了葉片雙曲面砂帶磨削力的精確控制方法。肖貴堅等[15]提出了一種面向型面精度一致性的砂帶磨削新方法,一方面通過砂帶周期性的往復運動結合自銳式磨削原理,實現型面銑削殘差層的高效去除;另一方面通過砂帶周期性的自動更新,保證各葉片的型面精度在同一截面具有高一致性。闡述并建立了面向型面精度一致性的砂帶磨削新方法及其磨削控制方程。Xiao和Huang[16]對航發葉片邊緣當量自適應砂帶磨削方法進行了研究，對砂帶磨削后的表面粗糙度進行了分析，結果表明在砂帶磨削后表面粗糙度≤0.25 μm，且表面呈現壓應力狀態；藺小軍等[17]采用柔性拋光技術和控制拋光軸矢量來實現砂帶與葉片型面的有效貼合，砂帶磨削技術的發展極大地提高了葉片表面加工的質量。

由上述分析可以看出，對于鯊魚皮仿生表面的加工，大多采用砂輪磨削的方式，國內外缺少砂帶磨削仿生表面的形成和對葉片、整體葉盤等零件仿生表面加工的研究。本文將針對葉片鯊魚皮仿生表面進行研究，首先，分析了微觀仿生鋸齒狀表面典型結構特征，基于單顆粒砂帶磨削模型，研究了單顆粒砂帶磨削去除機理；然后，建立了砂帶磨削多顆粒參數化數學模型，提出微觀仿生鋸齒狀表面砂帶磨削方法；最后，以鈦合金葉片型面為對象，搭建以鈦合金為典型材料的微觀仿生鋸齒狀表面砂帶磨削基礎實驗平臺，進行微觀仿生鋸齒狀表面的試驗驗證。

1 微觀仿生鋸齒狀表面磨削機理

1.1 單顆粒數學模型及其磨削特征分析

圖1中各種溝槽形狀的最佳幾何形狀對比數據主要來源于Bechert等[18]的研究，其中h為溝槽高度、s為溝槽寬度、α為溝槽的夾角、w為溝槽尖端平面寬度。對于鋸齒狀溝槽結構而言，最大減阻量可達5%左右，是耐用度最佳的結構之一，最佳幾何參數為：h/s=1，α=60°；對于刀刃狀溝槽結構而言，最大減阻量可達9.9%左右，是減阻量最優的結構之一，且減阻量的大小隨著溝槽厚度的增加而減小，耐用度不佳，最佳幾何參數為：h/s=0.5。

圖1 鯊魚皮衍生微觀仿生表面參數化3D模型[18]Fig.1 Parametric 3D model of micro-shark skin inspired structures bionic surface [18]

刀片型結構具有最佳減阻效果但容易失穩，在實際中鋸齒結構因其具有幾何穩定性而被廣泛采用，其具體結構參數設計如圖2所示[19]，其中α1為溝槽底角，α2為鋸齒溝槽頂角，v為流體線速度，b1、b2為承載邊受力長度，A、B、C為其中一個鋸齒狀三角形的3個頂點。類似于鯊魚皮表面溝壑結構，承載面是試件在流體中直接接觸并且承受力的一面，其二維截面正視圖中對應的邊為承載邊，承載邊的大小直接決定了承載面面積的大小，當流體中承載面的受力不變的情況下，增大承載邊的長度可以增加承載面的面積，從而可以減輕承載面所受的壓強，相應的可以減少微觀鋸齒狀仿生表面的阻力。

如圖2所示，在ΔABC中，由三角形余弦定理以及面積公式可以得到b1、b2與s、h、α1之間的關系式為

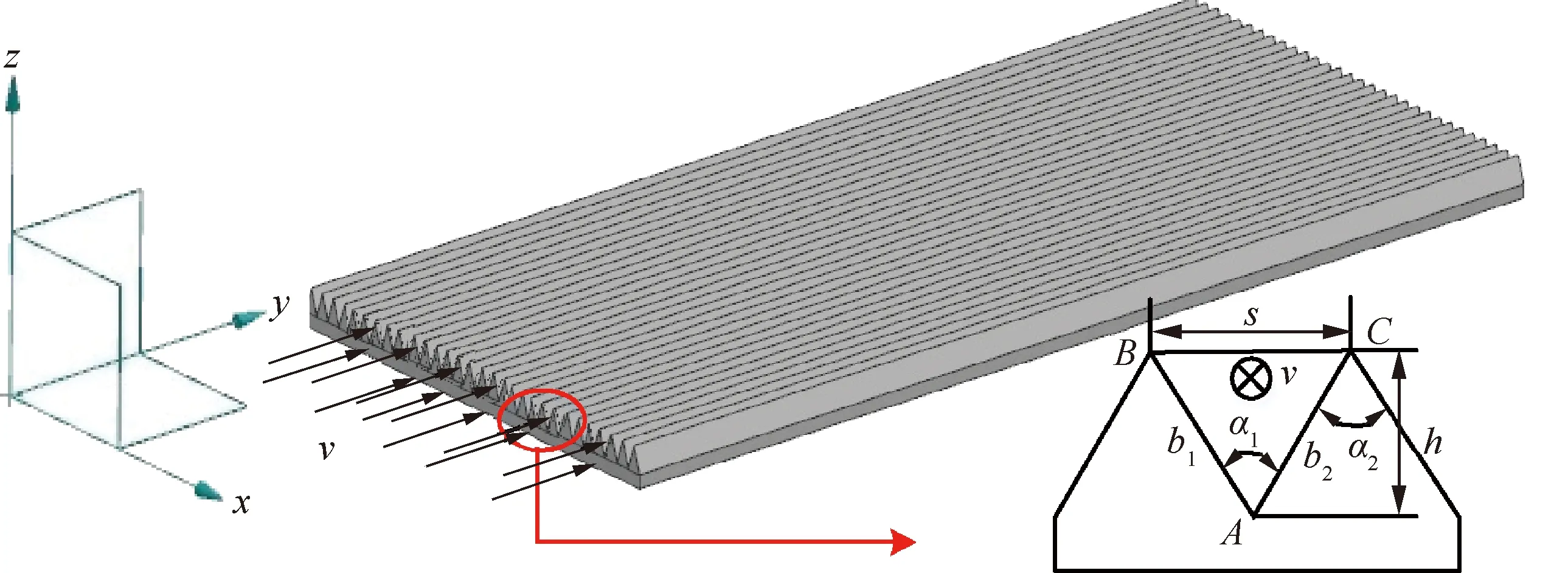
圖2 微觀仿生鋸齒狀表面示意圖[19]Fig.2 Schematic diagram of micro bionic zigzag surface[19]

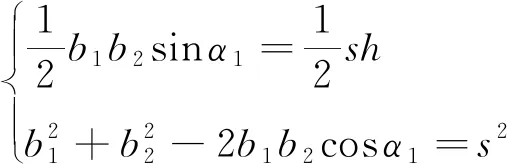
化簡可得

可得承載邊長度b1、b2由s、h、α1表達的關系式為

通過調整參數s、h、α1的大小，可以對承載邊b1、b2進行控制，從而對微觀鋸齒狀仿生表面的減阻等性能進行調控。

要實現上述特征表面的磨削，需要進一步探究單顆粒磨削的表面形成過程，在此基礎上來研究微觀仿生鋸齒狀表面砂帶磨削的方法。在砂帶磨削材料去除原理研究中，重慶大學黃云等在《現代砂帶磨削技術及工程應用》一書中研究了單顆磨粒切刃切除材料的原理模型，分析了單顆磨粒切刃切除材料運動過程中的材料去除機理，如圖3 所示，其中Ft為單顆磨粒切向力，Fn為單顆磨粒法向接觸壓力，2θ為磨粒錐頂角，Bm為與磨粒進給垂直方向最大寬度，Hm為磨痕斷面最大谷底高度。

圖3 砂帶磨削單顆粒模型Fig.3 Single particle model for belt grinding

磨粒切刃在材料表面的平均最大磨痕斷面面積為

(1)

磨痕斷面最大谷底高度為

(2)

又因為

(3)

將式(3)代入式(2)推出Hm與Bm的關系：

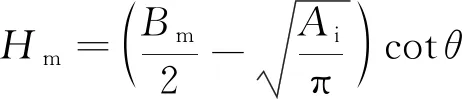
(4)

式中：HV為材料的維氏硬度；k為磨粒與工件相互作用影響因子，通常取1.08；Ai為磨粒端部小平面面積；m為接觸區切刃密度。

從式(2)可以看出，磨痕斷面最大谷底高度Hm同Fn、m、HV有關。當被加工材料確定后，材料所對應的維氏硬度為一定值，Hm、Fn和m呈冪函數分布，Fn越大、m越小，得到的Hm也越大。從式(4)可以看出，最大谷底高度Hm和最大寬度Bm之間存在線性關系。

單顆粒砂帶磨削材料去除機理已經充分地證明了砂帶磨削可以有效的控制Hm和Bm，因此，采用砂帶磨削達到了形成理想微觀仿生鋸齒狀表面的條件。在試驗中為了控制Hm和Bm的大小，形成微觀仿生鋸齒狀表面，可以通過改變Fn、m、vp等工藝參數來實現，同時m與P呈反比例關系，故可以用P表示m。

1.2 砂帶磨削多顆粒磨削去除模型

圖4中取磨削平面中垂直于磨具系統軸線的橫剖面圖進行分析，砂帶以線速度vs繞著直徑為d0的接觸輪中心進行旋轉，工件以線速度vp沿x軸方向做勻速進給運動。在運動經過時間t時，磨具系統中砂帶由A點轉動到B點，轉動了β角，工件由C點運動到B點，此時在多顆粒共同作用下完成從接觸工件到切削的整個過程，圖中區域ABCD就是多顆磨粒共同作用去除的部分材料。

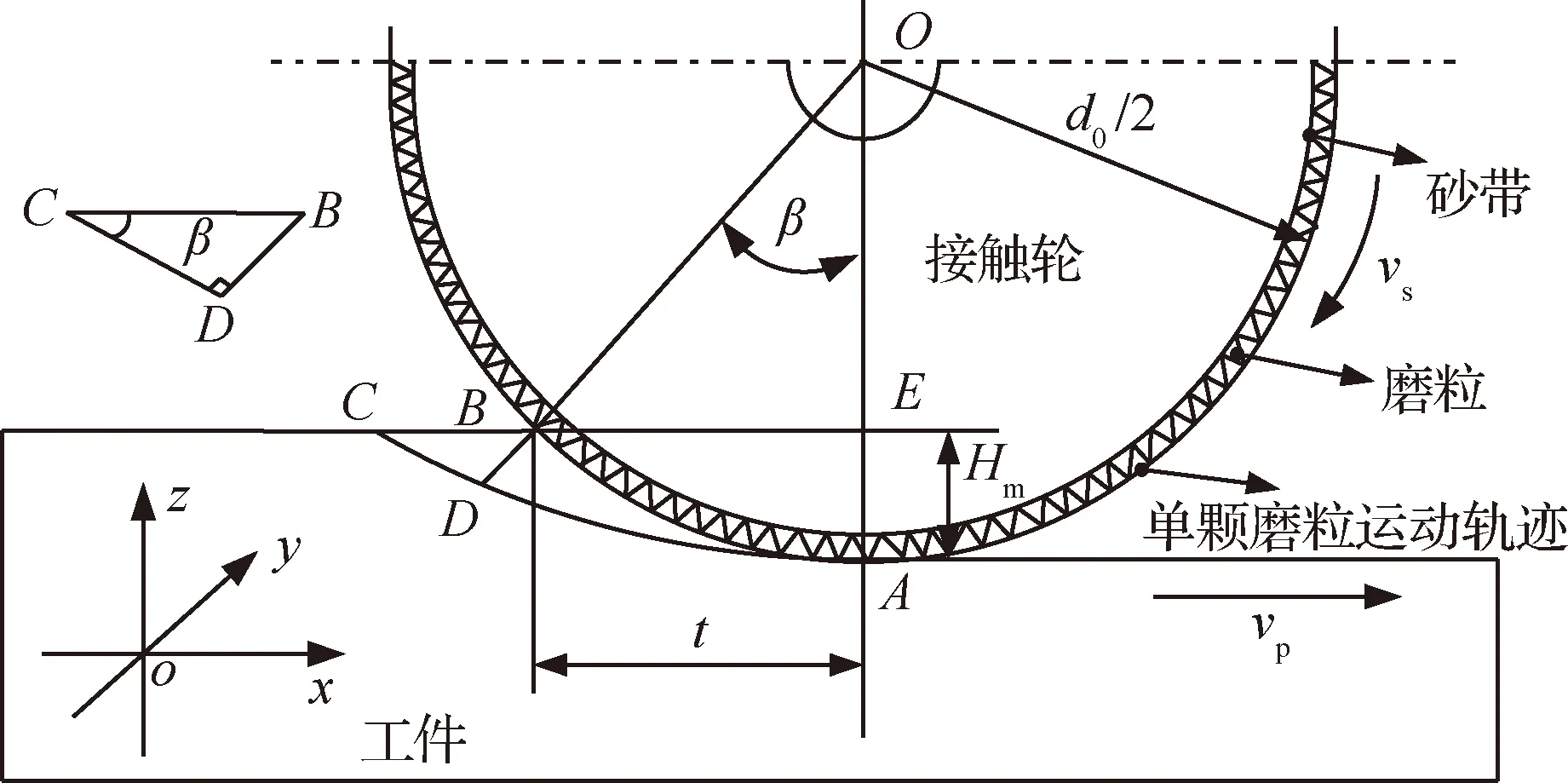
圖4 砂帶磨削多顆粒切削運動示意圖Fig.4 Schematic diagram of belt grinding movement of multi particles

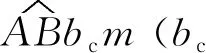
(5)

由于磨削過程為微量切削，且切削時間t較小，故而將ΔBCD近似看成一個以角∠CDB為直角的直角三角形，由幾何知識可得

BD=BCsinβ

又因為在直角三角形ΔOBE中，根據幾何知識可得

cosβ=OE/OB=(d0/2-Hm)/(d0/2)=(d0-2Hm)/d0

由此，可以推出:

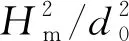
(6)

正如前文研究中的假設，在研究分析過程中忽略砂帶的單顆粒磨損的影響，故由式(4)可得砂帶中的單顆粒磨削溝槽最大深度為

(7)

將式(7)代入式(6)可得砂帶中單顆磨粒的最大切削深度為

(8)

式中:Kc為單顆粒切削深度系數，由此可以看出，在砂帶磨削磨具系統參數不變的情況下，砂帶磨削中的hc與vp和Fn成正比，與vs成反比。其表達式為

(9)

從式(9)可以看出，砂帶中的單顆粒切削深度系數Kc與m、θ、k、bc、HV等有關。

為了研究砂帶磨削參數化數學模型,將hc作為微觀仿生鋸齒狀表面的深度h；將Bm作為微觀仿生鋸齒狀表面的寬度s；將2θ近似為微觀仿生鋸齒狀表面的夾角α1；從而得到微觀仿生鋸齒狀表面砂帶磨削參數化計算公式為

(10)

從單顆粒磨削參數化數學模型中可以看出，砂帶磨削形成微觀仿生鋸齒狀表面溝槽的高度與工件進給速度、砂帶旋轉速度、磨削正壓力以及磨具系統的固有參數等有關，微觀仿生鋸齒狀溝槽的寬度與磨削正壓力以及磨具系統的固有參數有關，其夾角主要與砂帶磨粒的形狀有關。

2 微觀仿生鋸齒狀表面磨削規劃及其實驗

2.1 葉片微觀仿生鋸齒狀表面砂帶磨削方法

為實現微觀仿生鋸齒狀表面的磨削，設計了如圖5所示的砂帶磨削運動方案。數控磨床通過接觸桿控制接觸輪并使之緊貼砂帶與工件表面接觸而產生力Fn，同時磨床主軸帶動砂帶的高速旋轉而與工件表面產生力Ft，在力Fn與力Ft共同作用下實現砂帶的磨削過程。

其磨削運動形式主要是接觸桿帶動磨頭以恒定進給速度vp、進給步距P在試件表面沿著Y軸方向做周期為T的往復運動，運動距離為試件長度L，與此同時砂帶主軸以線速度vs旋轉，并通過接觸桿對試件表面施加恒定接觸力F，保證砂帶可以與試件表面有效的貼合，從而進行材料有效地去除。通過施加在接觸桿/輪上的力F帶動砂帶沖擊式的磨削運動，實現砂帶微切削快速累積運動，既快速去除余量又能保證粗糙度，使銑削殘差層得以高效的去除，同時在表面形成微觀仿生鋸齒狀。

如圖5所示，試件在運動過程中，受接觸桿作用，由式(10)可以得出，微觀仿生鋸齒狀溝槽的高度h同力Fn呈冪函數分布。為計算方便，本試驗選擇了φ=90°(即，砂帶和接觸桿/輪垂直方向施加力于試件表面)進行后續砂帶磨削試驗。

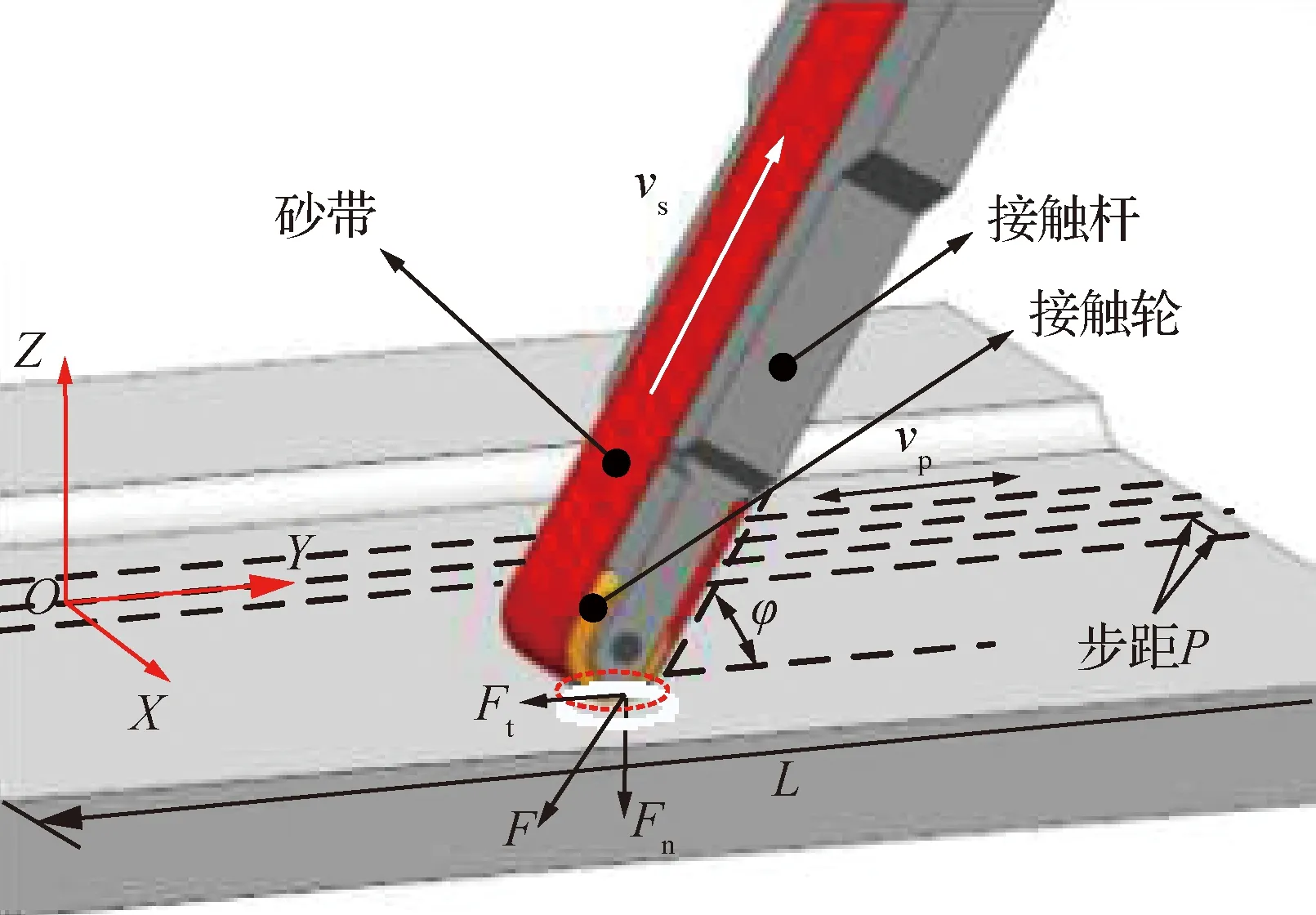
圖5 微觀仿生鋸齒狀表面砂帶磨削方法Fig.5 Micro bionic zigzag surface using belt grinding method

在砂帶磨削過程中，磨頭進給循環周期T由3部分時間組成：① 磨頭在試件長度方向來回直線進給運動時間；② 磨頭抬起落下的緩沖時間；③ 試件進給步距P的時間，故T可計算得：

(11)

式中：L為試件長度；h1為磨頭抬離工件表面高度；v步為機床步進電機進給線速度。

2.2 實驗裝置及其方法

選用某型號航空發動機壓氣機鈦合金葉片進行微觀仿生鋸齒狀表面砂帶磨削實驗驗證，實驗采用由重慶三磨海達磨床有限公司和重慶大學共同研制的七軸六聯動自適應數控砂帶磨床作為加工磨床，磨床具體結構如圖6所示。

圖6 MGY5540A-7NC 數控砂帶磨床Fig.6 MGY5540A-7NC CNC belt grinding machine

由于砂帶磨削過程中接觸輪本身具有的弱剛性及磨床U軸在Z軸方向上具有一定范圍內的彈性運動，使得該磨床在對葉片等復雜曲面加工過程中具有一定的“柔性”特征。該砂帶磨床的核心是具有補償功能的數控砂帶磨具系統，該磨具系統主要由砂帶、接觸輪、接觸桿等組成。磨具系統與葉片的接觸為浮動接觸，磨頭的微小位移不會給葉片帶來大幅度磨削壓力的改變。該數控砂帶磨床不僅可以使砂帶和葉片進行有效的貼合，而且還可以最大程度地避免磨削過程中過切和過磨現象的產生。

本文對單顆粒模型磨削參數的分析驗證了微觀仿生鋸齒狀表面磨削的可行性；然后通過單顆粒模型計算了實際多顆粒砂帶理論上磨削的可行性和推導了微觀仿生鋸齒狀表面參數的理論計算公式；最后進行相關的試驗，檢測所加工出來的微觀仿生鋸齒狀表面參數，與理論計算出來的溝槽寬度s、溝槽高度h和實際的磨粒夾角α1進行分析驗證，具體如圖7所示。

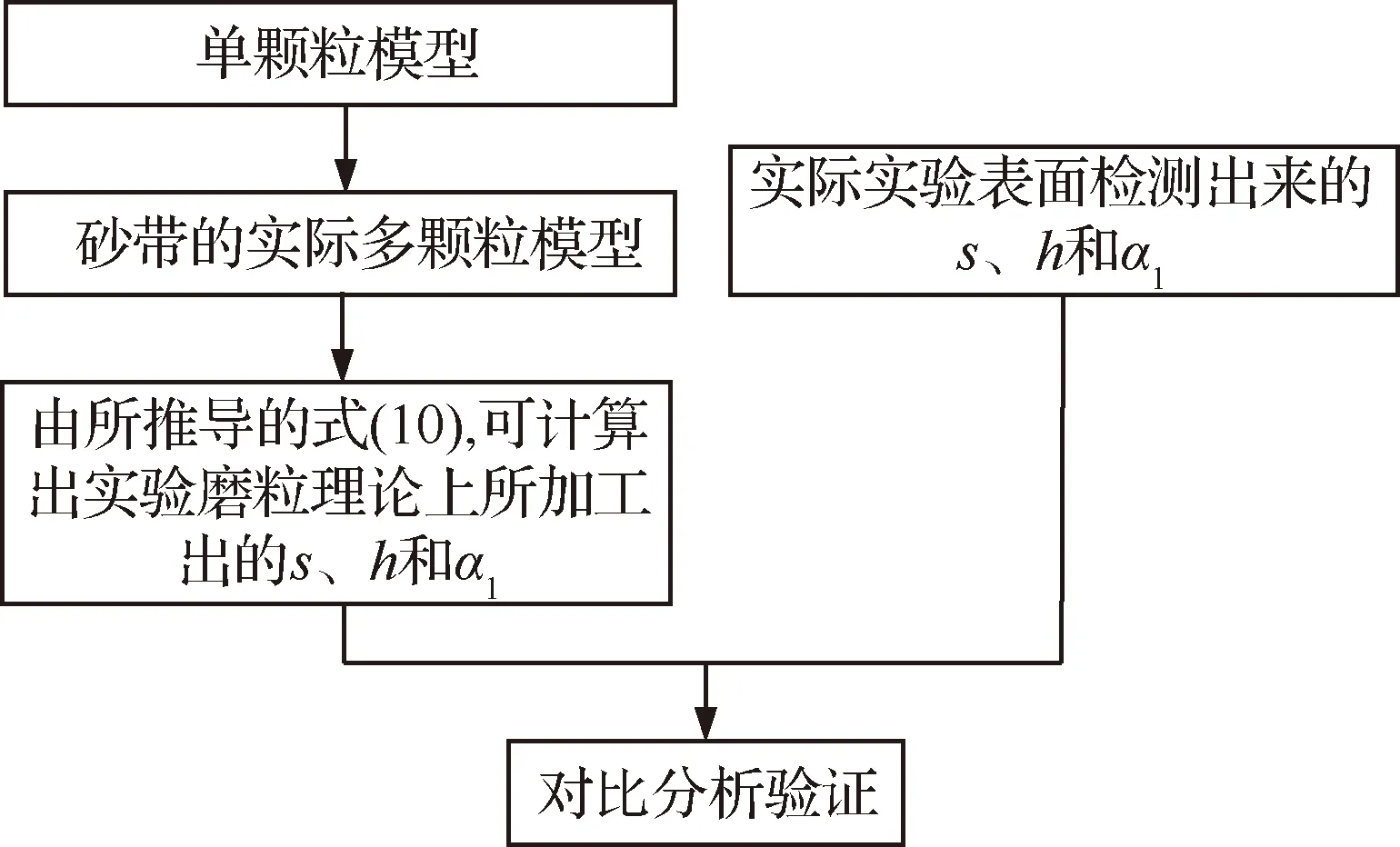
圖7 研究思路流程Fig.7 Chart of research idea

圖8為砂帶磨削微觀仿生鋸齒狀表面示意圖。結合實際的航發鈦合金葉片表面粗糙度要求[1]，擬加工表面參數選定為s=5～10 μm，h=5～10 μm和α1=60°[20]。由此可以推出砂帶磨粒大小應在50～100 μm之間，根據廠商粒度型號的分類，選用粒度號為 P240 的磨粒(其磨粒大小為60 μm)。使用 3M 陶瓷氧化鋁 XK870F 粒度號為 P240 和金字塔 237AA 粒度號為 P240 的砂帶，并采用表1的工藝參數來進行磨削實驗驗證。砂帶磨削素有“冷態磨削”之稱，故本次實驗磨削條件為干磨。

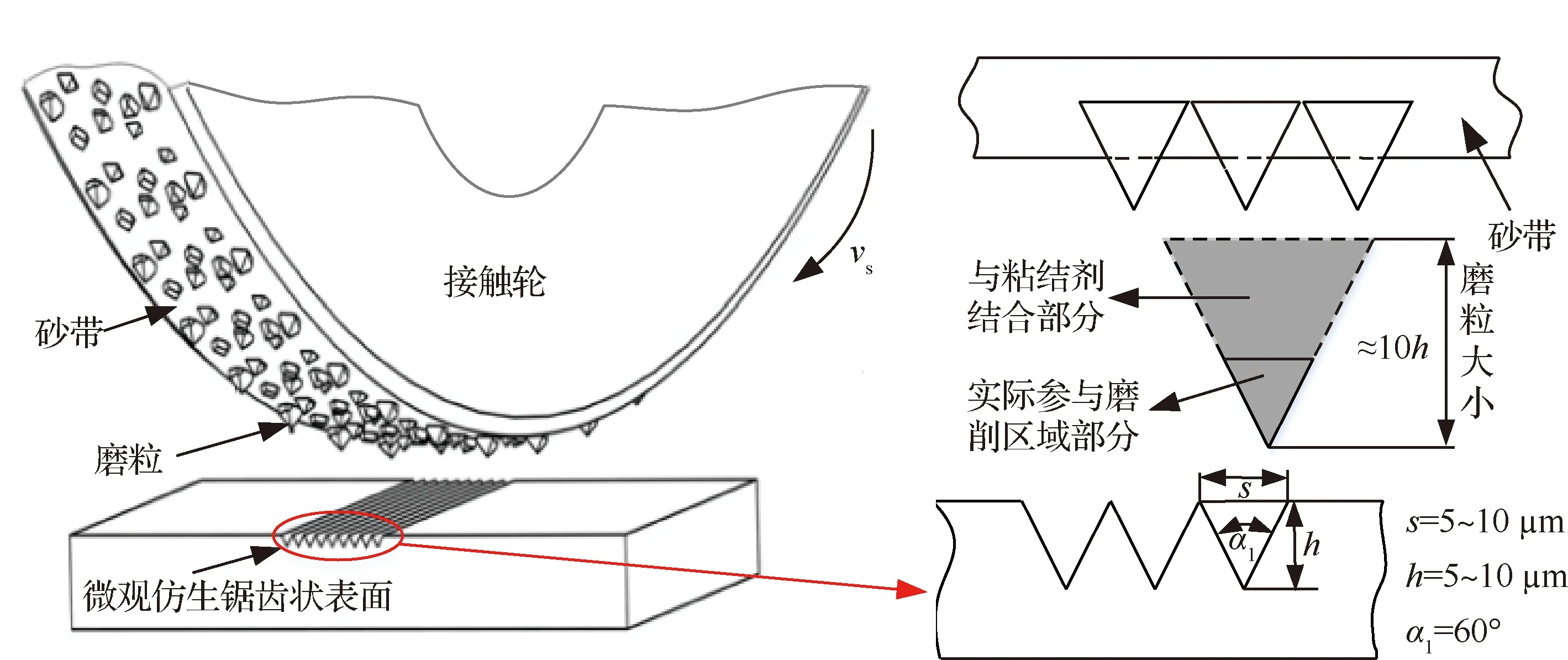
圖8 砂帶磨削微觀仿生鋸齒狀表面示意圖Fig.8 Schematic diagram of micro bionic zigzag surface using belt grinding

表1 葉片砂帶磨削工藝參數Table 1 Belt grinding process parameters for blade

3 葉片微觀仿生鋸齒狀表面磨削分析

為了更直觀有效地反映砂帶磨削后的微觀仿生鋸齒狀表面結構參數，采用掃描電子顯微鏡 SEM 和形狀測量激光顯微鏡 VKL-X1000 分別拍攝試件表面的二維和三維形貌，同時，結合三維模型重構理論中的曲面擬合方法對試件拍攝后的微觀仿生鋸齒狀三維形貌結構參數進行數據采集，來分析表面形貌的參數。

二維形貌是對試件表面分布狀態以及形態的一種直觀性表達，可以通過掃描電子顯微鏡拍攝圖片后進行觀察。對陶瓷氧化鋁砂帶磨削后的表面進行后期的分析處理，得到砂帶磨削后微觀仿生鋸齒狀表面 SEM 二維形貌，如圖9所示。從圖9中可以直觀地看出表面結構分布較均勻，鋸齒形溝槽結構，且測得圖形中溝槽寬度在5.5 μm左右。

圖9 磨削后微觀仿生鋸齒狀SEM二維形貌表面Fig.9 SEM of two-dimensional morphology of micro bionic zigzag surface after belt grinding

三維形貌是對試件表面微觀仿生鋸齒狀結構分布狀態以及形態的一種直觀性表達，可以通過形狀測量激光顯微鏡 VKL-X1000 拍攝圖片后進行觀察。分別對試件磨削前后的表面三維形貌圖進行后期的分析處理，結果如圖10和圖11所示，對比試件磨削前后三維形貌表面，可以看出磨削之后的表面減少了表面凸凹不平和表面燒傷等缺陷，表面質量得到了提高。

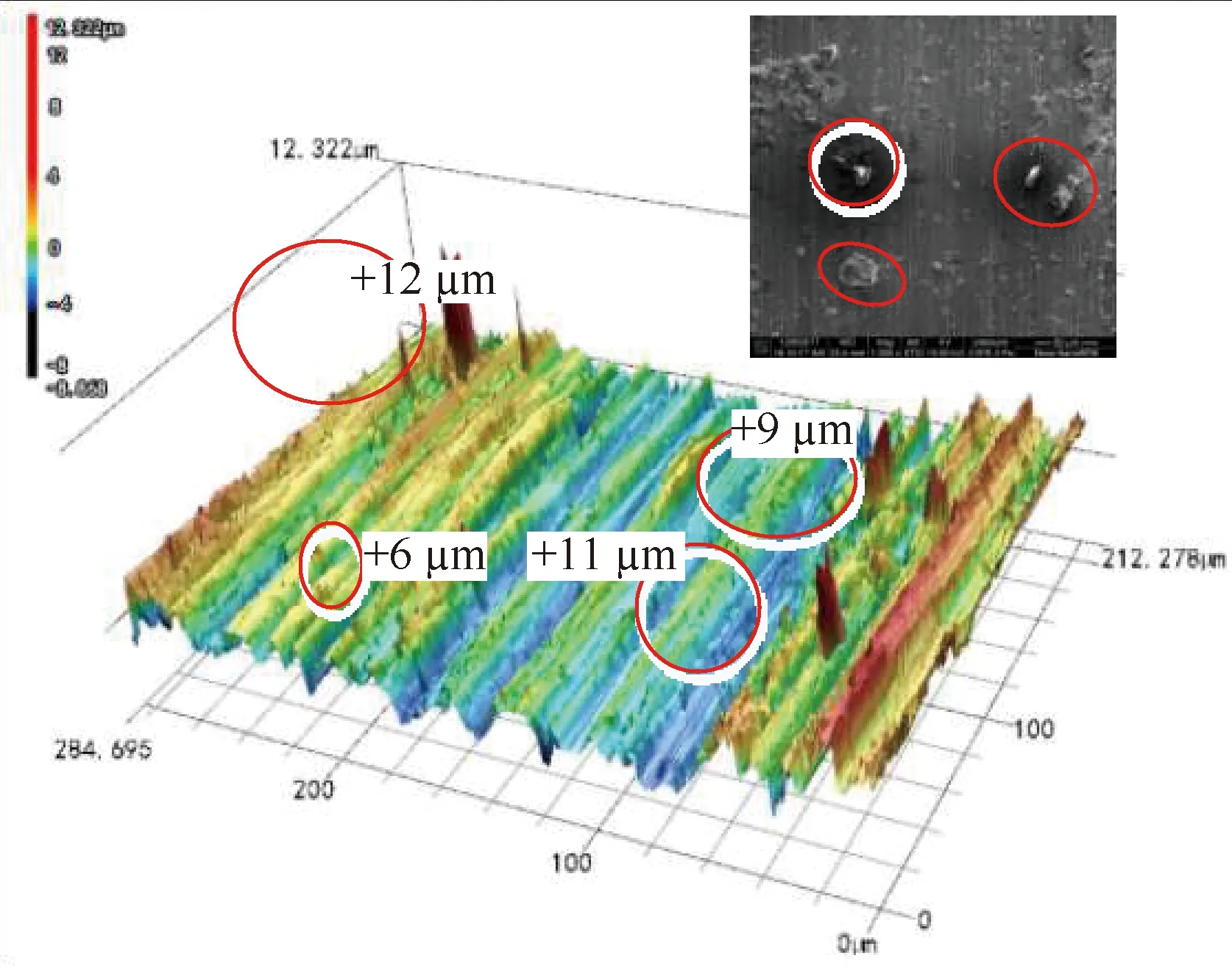
圖10 砂帶磨削前表面微觀三維圖Fig.10 Three-dimensional morphology surface before belt grinding

將圖11中用序號標出的溝槽進行參數測量分析對比，用1.2節中式(10)算出的理論微觀仿生鋸齒狀表面溝槽寬度s、溝槽高度h和實際的磨粒夾角α1與實際測得的參數進行對比，得到圖12。

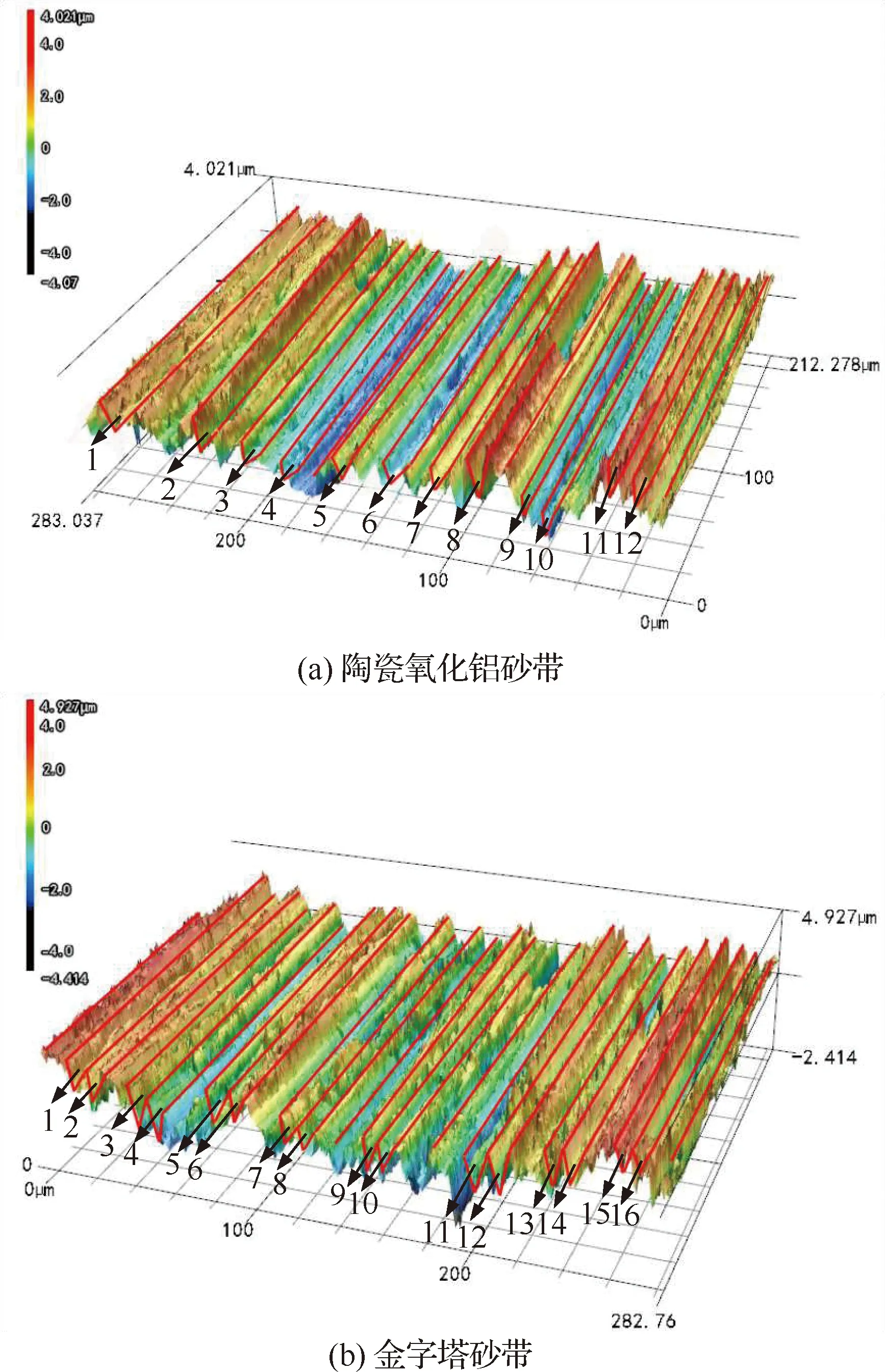
圖11 砂帶磨削后微觀仿生鋸齒狀表面三維圖Fig.11 Three dimensional morphology of micro bionic zigzag surface after belt grinding

由圖12(a)和圖12(b)對比發現，實際的溝槽寬度s和溝槽高度h都明顯小于理論值，這是由于葉片的弱剛性和接觸輪的彈性所造成的。在磨削過程中，葉片由于受磨削力的影響，在磨削時會產生一定的彎曲變形，接觸輪在接觸葉片磨削的區域也會產生彈性變形，使得實際磨粒磨削的去除材料深度比理論的小，從而磨削所產生的表面尺寸實際值比理論值小；并且在磨削過程中存在著磨粒的磨損現象，使得磨粒變小，進一步影響了實際磨削產生的微觀仿生鋸齒狀表面尺寸。磨粒的磨損主要是由于磨粒的切削刃被磨平或者斷裂，使得h與理論值的差距比s與理論值的差距大。由圖12(a)和圖12(b)還可以看出，金字塔砂帶磨削出來的溝槽寬度s和溝槽高度h總體上比陶瓷氧化鋁小，這是由于金字塔砂帶有著獨特的金字塔結構，氧化鋁/碳化硅礦砂，樹脂膠，表面加有助磨劑，使得金字砂帶的磨粒磨損比陶瓷氧化鋁砂帶小，實際磨削效果更好。

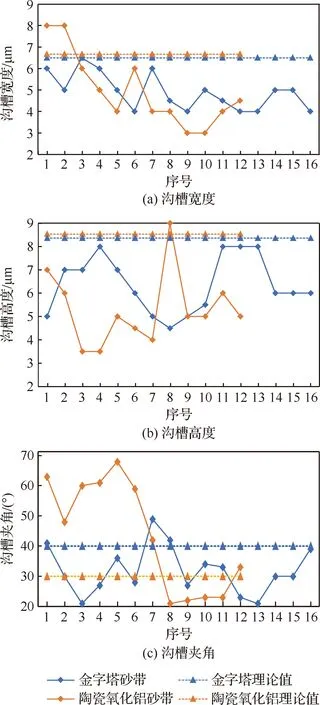
圖12 兩種砂帶磨削表面參數對比Fig.12 Comparison of surface processed by two kinds of belt grinding parameters

對于溝槽夾角α1，由于在砂帶磨削過程中的磨粒磨損和磨粒大小的不均勻性，使得溝槽夾角有明顯的波動，且陶瓷氧化鋁相對于理論值的波動性更大。明顯的用金字塔砂帶磨削出來的微觀仿生鋸齒狀表面溝槽夾角α1更小而且溝槽寬度、高度和夾角一致性更好，磨削表面線路更細致均勻，如圖13所示，這是由于金字塔砂帶的磨粒分布和大小更均勻，說明了微觀仿生鋸齒狀表面的參數與砂帶磨粒分布和大小有相關性。

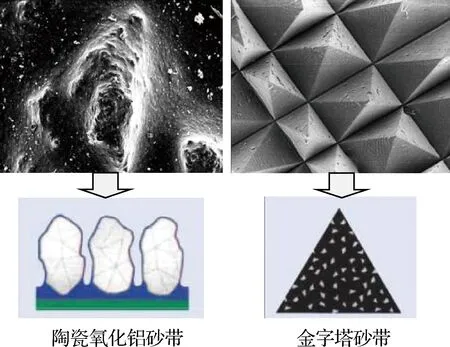
圖13 兩種砂帶形貌示意圖Fig.13 Schematic diagram of morphology of two kinds of belts

砂帶磨削后的微觀仿生鋸齒狀表面主要以鋸齒形溝槽為主，其中溝槽的寬度在2.5 ～8 μm之間，平均值為4.91 μm；溝槽的高度在3.5～9 μm之間，平均值為5.91 μm；溝槽的夾角在28°～68°之間，平均值為42.3°。

4 結 論

1) 對微觀仿生表面典型結構進行了分析，提出了將鋸齒形溝槽結構作為葉片的微觀仿生鋸齒狀表面。通過對單顆粒的砂帶磨削去除機理的研究，建立了砂帶磨削多顆粒參數化數學模型。最后，搭建了以鈦合金為典型材料的微觀仿生鋸齒狀表面砂帶磨削基礎實驗平臺。

2) 通過砂帶磨削方法實現了微觀仿生鋸齒狀表面的形成；砂帶磨削后的葉片表面減少了凸凹不平和燒傷等缺陷，表面質量得到了提高；砂帶表面磨粒分布情況能影響微觀仿生鋸齒狀表面溝槽形成的大小和均勻性。對砂帶磨削后的葉片表面進行檢測，結果表明通過砂帶磨削方法實現的微觀仿生鋸齒狀表面以鋸齒形溝槽為主。