整體壁板壓彎成形的形狀控制

張敏，田錫天，李波

西北工業大學 機電學院，西安 710072

隨著航空航天工業數字化設計及制造技術的快速發展，對現代飛行器的性能要求不斷提高，飛機設計結構發生了變化，開始大量采用整體結構設計，如整體框、梁、壁板等零件[1]。以鋁合金材料為主導的大型整體壁板是構成飛機氣動外形的重要組成部分，同時也是機翼、機身等的主要承力構件，因具有減重效果明顯、總體和局部剛度好、強度高等優點[2-3]，在航空航天等領域獲得了廣泛的應用。

作為飛機最大的承載部件，現代大型飛機機翼翼盒的結構設計也采取了整體壁板的結構形式。此類壁板將機翼蒙皮與長桁、肋、對接接頭以及其他可附帶的結構件(如注油口框等)集合為一體[4]，大大減少了結構零件的項目和數量。但是由于此類壁板結構復雜，尺寸變化較大，外形精度要求高，如何成形是整機研制過程中必須解決的關鍵技術之一。

壓彎成形(指增量壓彎成形)是由專用壓力機驅動壓頭在整體壁板表面按一定的路徑分段逐點進行局部三點彎曲變形，最后使整個壁板表面彎曲為所需型面的成形工藝，其基本原理是靠逐次的變形累積產生整體的變形[5]，如圖1所示，具有設備工裝簡單、變形力大、生產周期短和對外形曲率適應性強等特點，是帶筋整體壁板的局部彎曲成形，或帶有加厚橫向凸臺和口蓋周圍的加強區及高筋條整體壁板的一種重要成形手段[6]。機翼整體壁板中厚度尺寸較大的對接接頭部分的成形就采用壓彎成形方法。但壓彎成形是一個十分復雜的彈塑性變形過程，卸載后伴隨著不同程度的回彈，導致壓彎成形質量難以保證和控制[7]，如對于復雜的鋁合金壁板，需要6個多月進行回彈誤差校正[8]。通過對飛機制造企業現場的調研證實：由于整體壁板壓彎成形方面缺少必要的科學理論和技術指導，工程實際中只能依靠操作者的經驗和技術水平，采用“試探法”“變壓邊量”“局部校形”等手段獲得理想外形，導致現有壓彎成形精度低，嚴重影響飛機的裝配質量和效率。

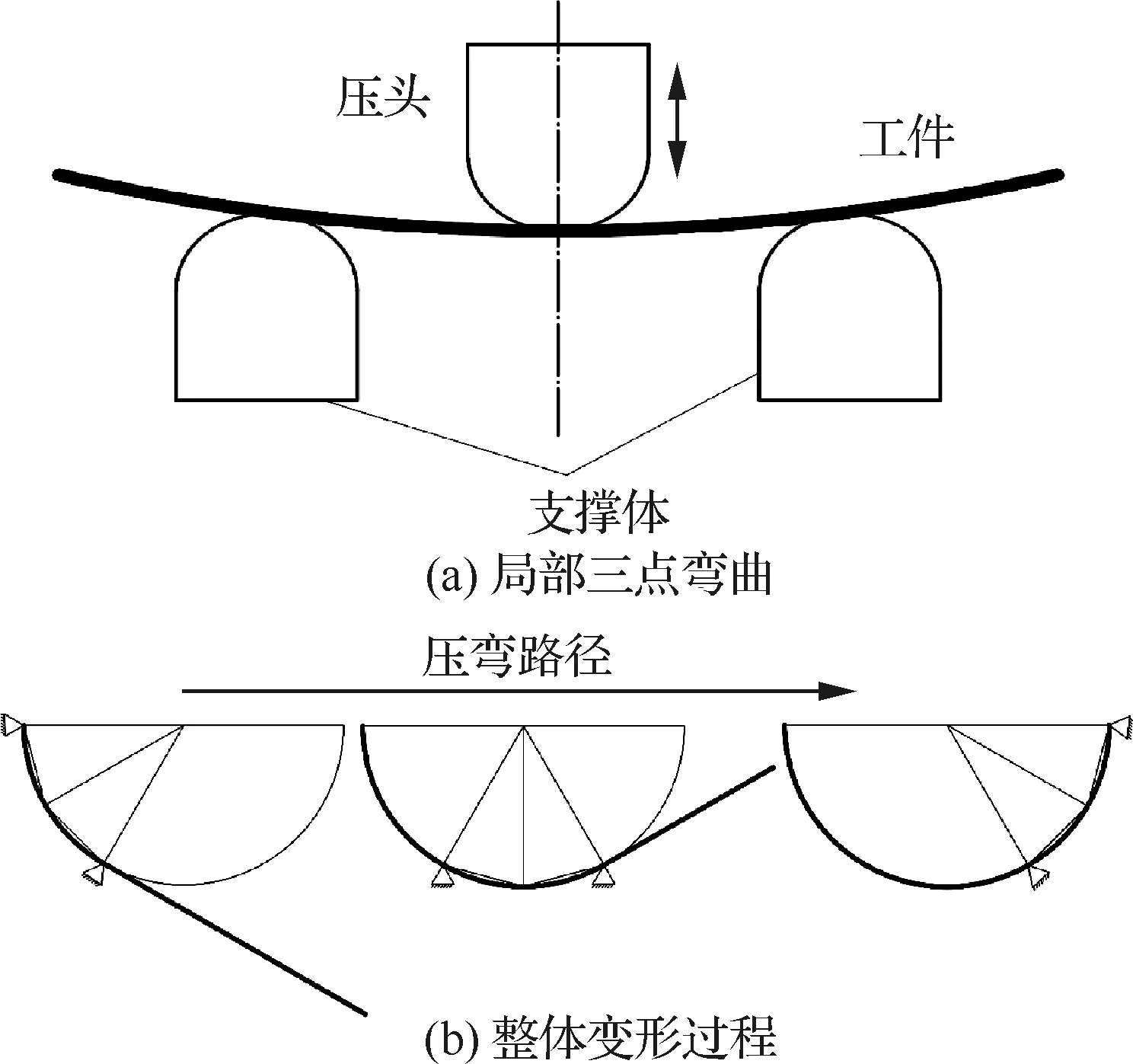
圖1 壓彎成形原理Fig.1 Press bend forming principle

目前，對壓彎成形形狀控制的研究主要有工藝控制和模面補償兩種方法[9]。工藝控制是通過調整凸模下壓量[10]、增加成形步驟[11-12]、提高成形溫度[13]等方式控制成形形狀，能夠在一定程度上減小回彈，但無法徹底消除。模面補償中應用較為成熟的是節點位移調整(Displacement Adjustment, DA)[14-17]方法，DA法是基于有限元模擬技術的閉環迭代法，通過修正模具型面進行回彈補償，獲得理想的零件成形精度，具有收斂性好、速度快和通用性強等優點，主要適用于采用模具成形的零件。

對于分段逐點三點彎曲成形的形狀控制研究，岳峰麗等[18]通過大量實驗建立了增量壓彎成形中壓下量和弧高值的一元線性回歸模型，實現了實際加工時工藝參數的初選，然后在壓彎過程中通過實時檢測理論弧高值和實測弧高值的誤差調整特征方程，保證成形精度。付澤民等[19]通過采用Abaqus有限元方法調整板材料多道次漸進折彎成形中各道次的模擬工藝參數，實現大尺度U形工件的精確成形。上述方法依然是依據經驗進行參數調整或者基于仿真進行參數調整。Yan等[20]建立了各壓點處下壓量與成形誤差的神經網絡模型，通過采用遺傳算法優化BP神經網絡的方法，獲得各壓點處最優的下壓量。但該方法僅適用于成形特定的曲率半徑，當曲率半徑發生變化時，需要重新建立神經網絡模型。

在上述研究的基礎上，基于彈塑性變形理論和幾何分析建立了壓彎成形局部變形下壓量預測模型，基于有限元法建立了壓彎成形整體變形有限元仿真預測模型；綜合考慮壓彎成形局部-整體變形精度，利用模具型面迭代思想(DA法)和逐步逼近思想，構建了壓彎成形輪廓曲線迭代模型。以Abaqus為平臺，對壓彎成形形狀控制方法進行驗證，為整體壁板壓彎精確成形提供理論指導。

1 整體壁板壓彎成形形狀控制方法

1.1 壓彎成形整體變形控制原理

通過文獻[21]可知，對于壓彎成形過程，即使有很精確的預測模型，也需要一定的反饋獲得目標成形形狀。因而，仍需通過迭代補償獲得目標成形曲線及其對應的下壓量大小。壓彎成形整體變形控制迭代原理如圖2所示。將彎曲線上相應節點處的位移作為調節變量，每個點的調節變量是一個二維矢量。當用來作為形狀補償的節點越多時，補償精度越高，但過多的節點會造成計算量過大。

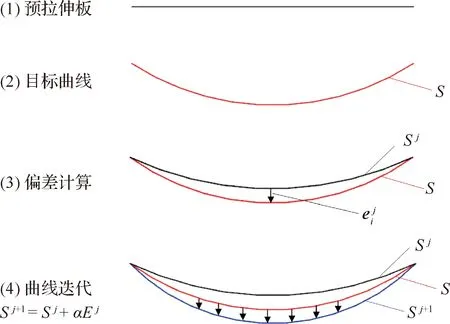
圖2 迭代原理Fig.2 Iteration principle

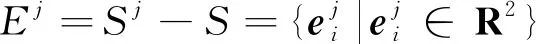
1≤i≤m, 1≤j≤m

(1)

壓彎成形時，首先計算控制節點與目標形狀之間的偏差，壓彎成形后對偏差進行補償。如對第j次成形后壁板形狀Sj進行補償，則第j+1次成形后壁板外形形狀為Sj+1，即

Sj+1=Sj+αEj1≤j≤m

(2)

式中：m為節點數量；α為補償因子，用以減小偏差補償量防止過彎，通常取0.7～0.9[17]。當成形后形狀偏差在允許誤差范圍內時，迭代補償結束。

1.2 壓彎成形整體變形控制過程

為了對壓彎件的成形精度進行評價，需要對壓彎件的成形精度進行定量計算。由于壓彎件外形輪廓為曲線，因此采用實際成形曲線與目標曲線之間的偏差作為成形精度，即按照一定距離提取成形曲線上的若干節點，所有節點與目標曲線節點之間距離的均方根作為整體偏差評價指標，用于控制整體變形，節點之間最大距離作為局部偏差評價指標，用于控制局部變形。當整體偏差和局部偏差均小于給定誤差值，則精度滿足要求。具體描述為

(3)

式中：Δli為節點與成形件目標曲線之間的距離；ξ、ζ為允許誤差。

根據壓彎成形形狀控制原理，提出壓彎成形形狀控制過程如圖3所示，主要分為兩步：第1步將壓彎成形局部變形解析預測得到的下壓量作為有限元分析的初始邊界條件，然后進行有限元計算；第2步以評價指標作為目標函數，結合補償因子更新參數值并將更新后的值返回到Abaqus中，直到精度滿足要求，停止迭代獲得最優下壓位移量。

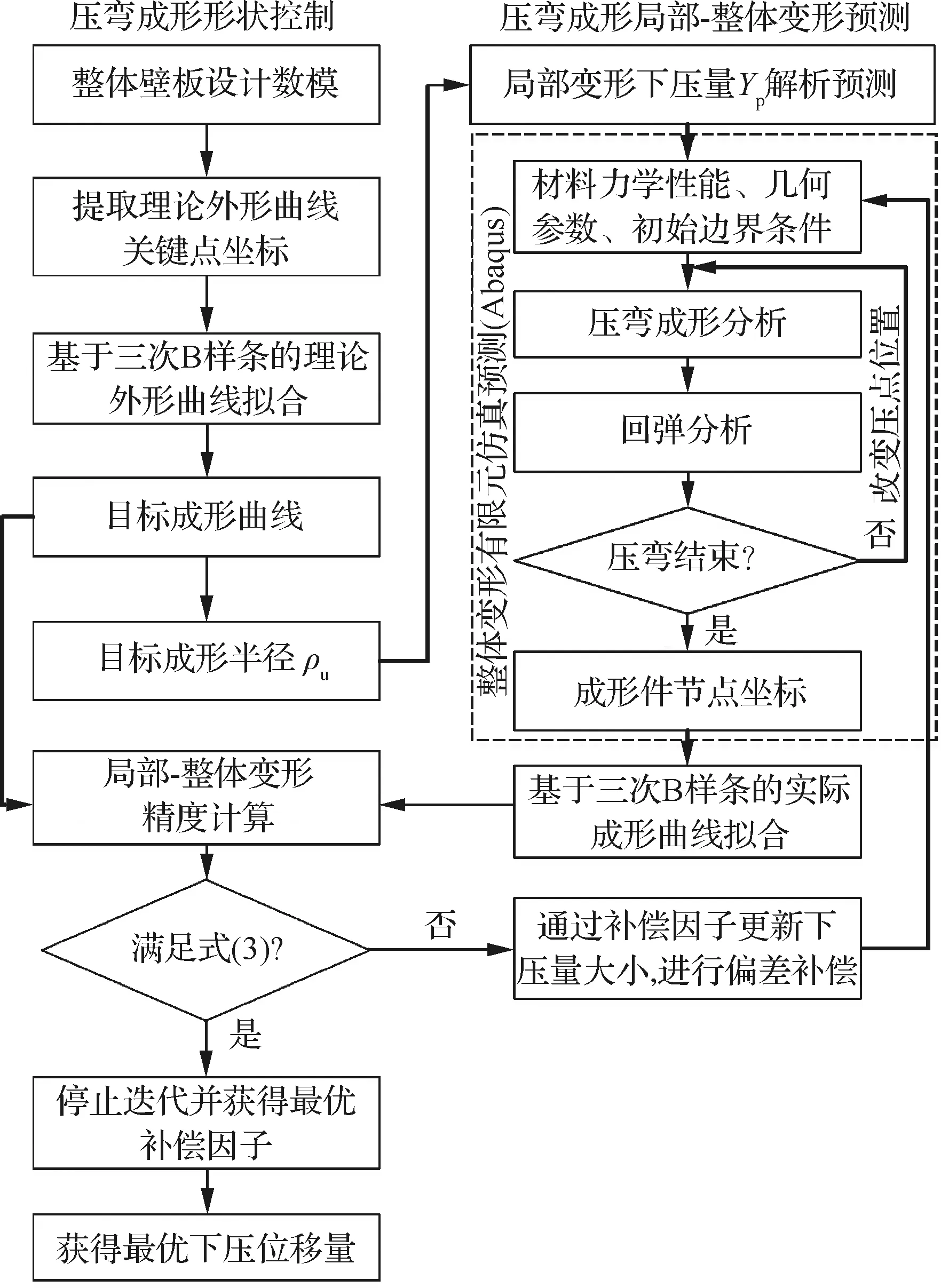
圖3 壓彎成形形狀控制過程Fig.3 Shape control process of press bend forming

2 整體壁板壓彎成形局部-整體變形預測

2.1 整體壁板試件設計

為方便在實驗室進行實驗，需設計整體壁板縮比試件模型。結合幾何相似性并根據實際機翼整體壁板，如圖4(a)所示，設計整體壁板縮比試件模型，如圖4(b)所示，整體壁板試件由對接接頭(即圖中所示的壓彎成形區域)和筋板兩部分組成，試件幾何尺寸為200 mm×60 mm×7.5 mm。

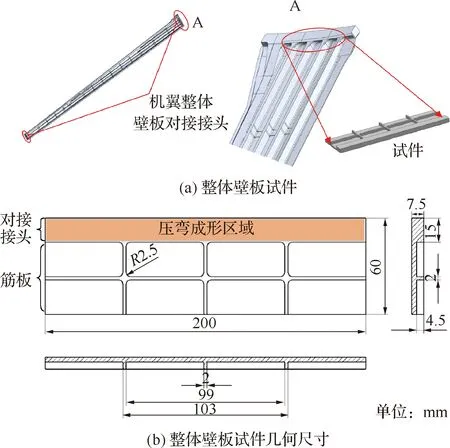
圖4 整體壁板試件Fig.4 Specimen of integral panel

2.2 材料模型

航空廣泛使用的7050-T7451鋁合金材料屬于高強度熱處理鋁合金，具有極高的強度和良好的耐磨性，主要用于制造飛機結構件，如飛機上、下翼面壁板、桁條等。單拉實驗是測定材料力學性能的基本實驗。根據國家標準GB/T228—2002《金屬材料 室溫拉伸實驗方法》設計拉伸實驗樣件，在CSS-44100電子萬能實驗機以1.5 mm/min 的速度進行單拉實驗，如圖5(a)所示。通過求取三組實驗的平均值，獲得材料工程應力-應變曲線，考慮變形過程中試件截面面積的改變，將工程應力-應變曲線轉換為真實應力-應變曲線，如圖5(b)所示。材料力學性能如表1所示。

表1 7050-T7451力學性能Table 1 Mechanical properties of 7050-T7451

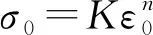
表2 硬化參數Table 2 Hardening parameters

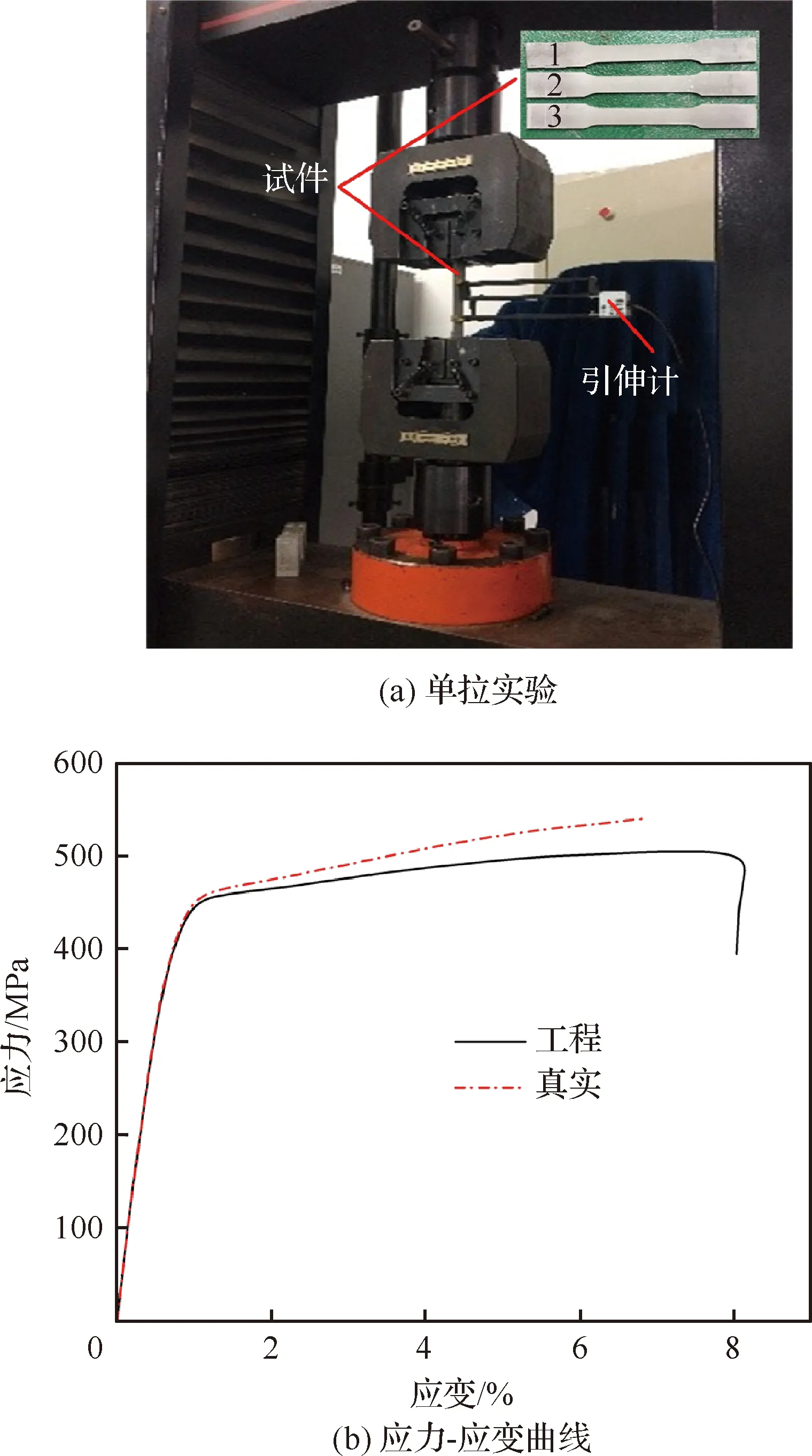
圖5 7050-T7451鋁合金應力-應變曲線Fig.5 Stress-strain curves of 7050-T7451 aluminum alloy

將不同硬化模型擬合得到的單拉應力-應變曲線與實驗數據進行對比，如圖6所示。從圖中可以看到，Ludwik硬化模型和H-S硬化模型的擬合效果相近，但Swift硬化模型擬合結果更接近于單拉實驗應力-應變曲線。因此，選擇采用Swift硬化模型。

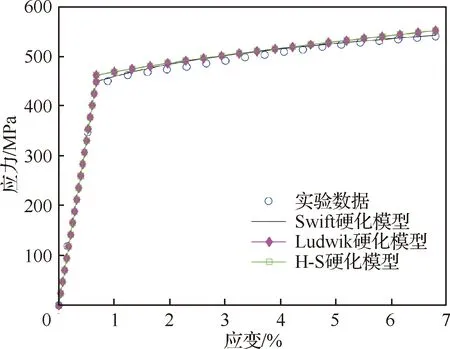
圖6 實驗和不同硬化模型得到的單拉應力-應變曲線Fig.6 Uniaxial tensile stress-strain curves obtained from experiments and different hardening models

2.3 整體壁板壓彎成形局部變形下壓量解析預測

根據壓彎成形原理，從局部變形和整體變形的角度對壓彎成形過程進行研究。理論解析法適用于分析局部三點彎曲變形這類簡單約束條件下的彎曲成形問題。因此，為了對整體壁板局部變形下壓量進行解析預測，將筋板部分簡化，以接頭部分截面作為受力截面。當下壓量為Yp時，壓彎成形局部變形如圖7所示。

圖7 下壓量與成形半徑Fig.7 Punch displacement and forming radius

通過幾何分析，可得：

(4)

式中：θ為卸載前的彎曲角；L為支撐體之間的跨距；ρn為卸載前中性層成形半徑；t為板料厚度；Rsb為支撐體半徑。

對式(4)采用三角函數平方關系進行變換，求得圖7中H的表達式為

(5)

下壓量Yp與成形半徑ρn之間的幾何關系為

Yp=ρn+t/2-H

(6)

將式(4)代入式(5)，聯合式(6)，得到下壓量的表達式為

(7)

基于經典回彈理論，彈塑性曲率變化等于彎矩引起的彈性曲率的變化，即回彈彎矩與加載彎矩在數值上相等，方向相反。因此，回彈后曲率變化為[22]

(8)

式中：ρu為卸載后中性層曲率半徑；M為壓彎成形局部變形時壓頭下方截面內彎矩；I為截面慣性矩，計算公式為I=ωt3/12(ω為截面寬度)。

由式(8)獲得ρu與ρn的關系為

(9)

式中：ρn為獲得目標成形半徑所需要的卸載前局部成形半徑；ρu可以理解為目標成形半徑。

將式(9)代入式(7)，可以得到目標成形半徑ρu與下壓量Yp之間的關系為

(10)

式中：彎矩M可以通過式(11)積分獲得，

(11)

式中：ρo和ρi分別為彎板最外側和最內側的曲率半徑；ρ為截面上一點的曲率半徑；σθ為切向應力，隨著采用的材料應力-應變關系的不同而具有不同的表達式。基于Swift硬化模型推導壓彎成形彈塑性區域切應力表達式為[23]

1) 彈性區域(ρn-ye<ρ<ρn+ye)：

(12)

2) 彎板內側塑性區域(ρi≤ρ≤ρn-ye)：

(13)

3) 彎板外側塑性區域(ρn+ye≤ρ≤ρo)：

(14)

式中：ye為彈塑性分界面到中性層的距離。

由式(10)～式(14)，下壓量Yp與目標成形半徑ρu、板料厚度t、支撐體半徑Rsb、跨距L及材料參數ν、E、K、n相關。在材料、板料厚度t、支撐體半徑Rsb和跨距L一定時，下壓量Yp只與目標成形半徑相關。通過數值迭代法計算獲得目標成形半徑所需要的下壓量大小的計算流程如圖8所示。先給定成形半徑的初始值，通過迭代計算直到獲得的成形半徑滿足目標成形半徑的誤差要求，即可計算得到獲得目標成形半徑的下壓量大小。

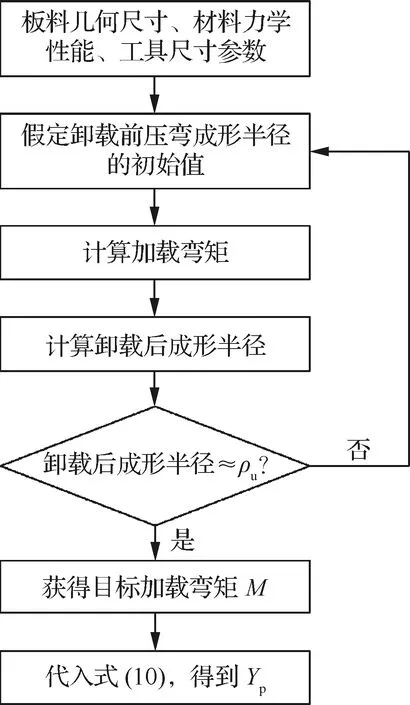
圖8 局部變形下壓量計算流程Fig.8 Flowchart of punch displacement calculation of local deformation

2.4 整體壁板壓彎成形整體變形有限元仿真預測

實際生產中生產人員更為關注的是壓彎結束后成形件的整體變形情況是否滿足精度要求，而整體變形精度由壓彎件的曲線形狀保證[24]。增量壓彎成形變形過程復雜，采用理論解析方法難以直接預測下一壓彎過程的彎曲力學行為，進而獲得增量壓彎成形卸載前后的外形輪廓曲線。有限元仿真是分析金屬塑性成形過程的有效手段。考慮到整體壁板壓彎成形時壓點之間相互影響以及筋板部分對壓彎成形的影響，為獲得準確的壓彎成形整體變形曲線，建立整體壁板試件壓彎成形整體變形三維有限元仿真預測模型。

采用有限元分析軟件Abaqus，建立壓彎成形限元模型。壓頭和支撐體的直徑分別為10 mm和15 mm，支撐跨距為50 mm。假設試件材料為各向同性[25]并服從Mises屈服準則，壓頭和支撐體為剛體，試件是可變形體；按照圖5和表1中單拉實驗獲得的材料參數賦予試件材料力學性能。試件網格劃分采用C3D8R網格，壓頭和支撐體采用剛體離散單元R3D4，網格尺寸均為1 mm×1 mm；壓頭和壁板以及支撐體和壁板的接觸面定義為面-面接觸，其中壓頭和支撐體設為主面，為了計算更易于收斂，接觸面之間設置有0.1 mm的間隙；實際壓彎過程中，壓頭、支撐體與試件之間的摩擦為干摩擦，在有限元模擬時根據文獻[26]，設置壓頭、支撐體和試件之間的摩擦系數為0.1；壓彎過程中支撐體的自由度完全約束，壓頭通過參考點在Y向施加位移載荷。建立的有限元仿真模型如圖9所示。為了保證收斂性和計算效率，采用Abaqus/Explicit對壓彎成形過程進行分析；載荷施加結束后，通過更改約束條件并去除壓頭和支撐體建立回彈模型，將載荷施加結束后的仿真結果作為試件的初始狀態，采用Abaqus/Standard對卸載回彈過程進行分析。

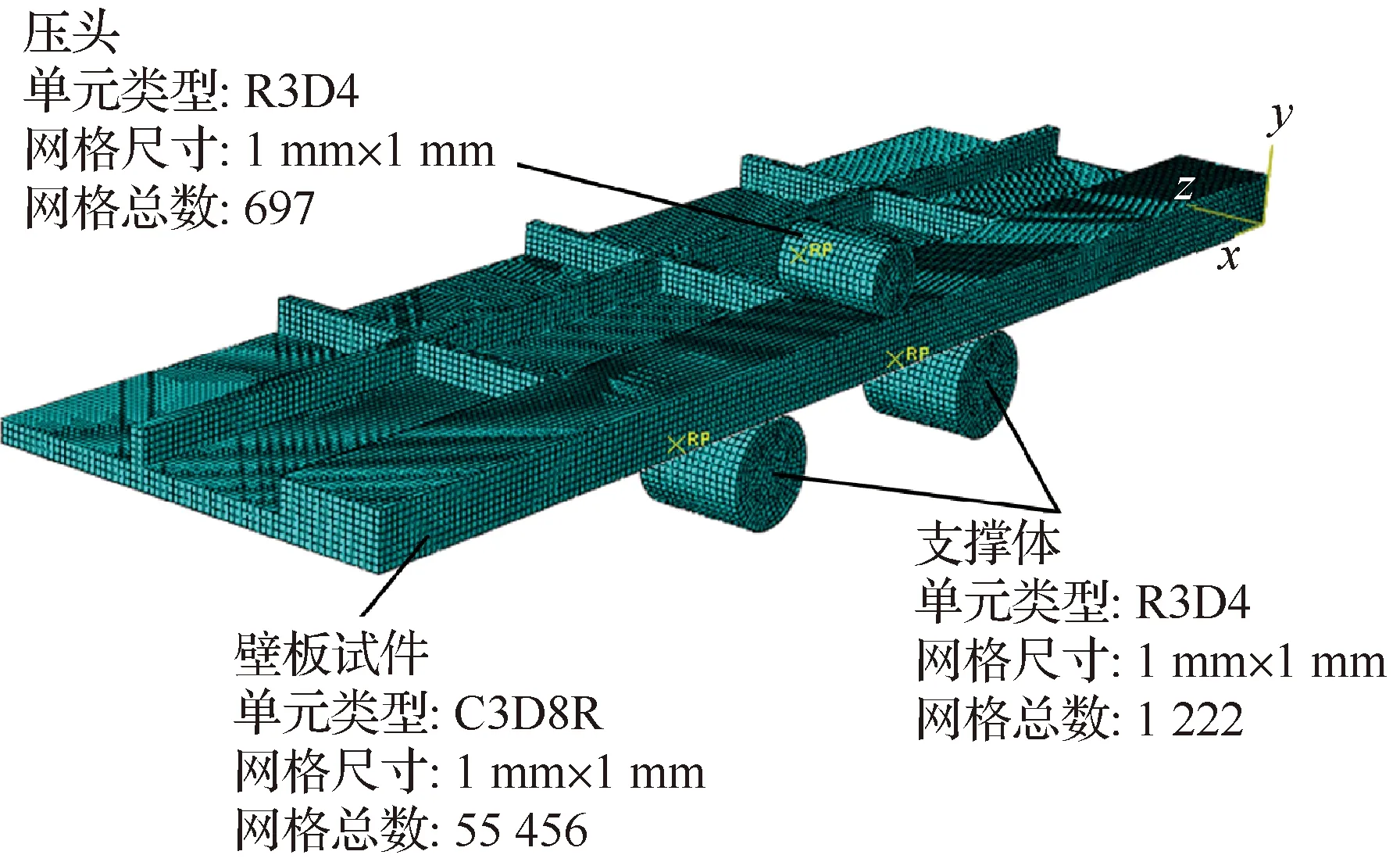
圖9 有限元仿真模型Fig.9 Finite element simulation model

在CSS-44100電子萬能實驗機上對壓彎成形有限元仿真預測模型進行實驗驗證。加載過程如圖10(a)所示，左右壓點位置的下壓量為3 mm，中間壓點位置的下壓量為3.5 mm，壓彎成形后的試件如圖10(b)所示，通過便攜式三維照相測量儀獲取成形試件的外形輪廓數據。

圖10 壓彎成形實驗Fig.10 Bending forming experiments

壓彎過程中彎曲力的準確性直接影響到有限元模擬的可靠性。因此通過實驗獲得的力-位移關系曲線驗證有限元模擬結果的有效性，同時對壓彎件的幾何形狀也進行對比。采用應用最為廣泛的三次B樣條曲線對成形后試件的外形曲線進行擬合，將壓彎過程中力-位移曲線和壓彎成形結束后獲得的成形試件外形輪廓曲線與壓彎實驗結果進行對比，如圖11所示。下壓量分別為3 mm 和3.5 mm時，壓彎過程中力-位移曲線實驗值與有限元模擬值之間的最大偏差分別為8.84% 和7.6%；壓彎結束后試件外形輪廓曲線實驗值與有限元模擬值之間的最大偏差為13.46%，所建立有限元模型精度滿足工程要求，可以用于壓彎成形精度控制研究。

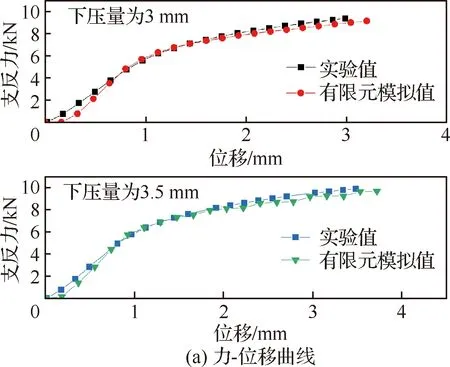
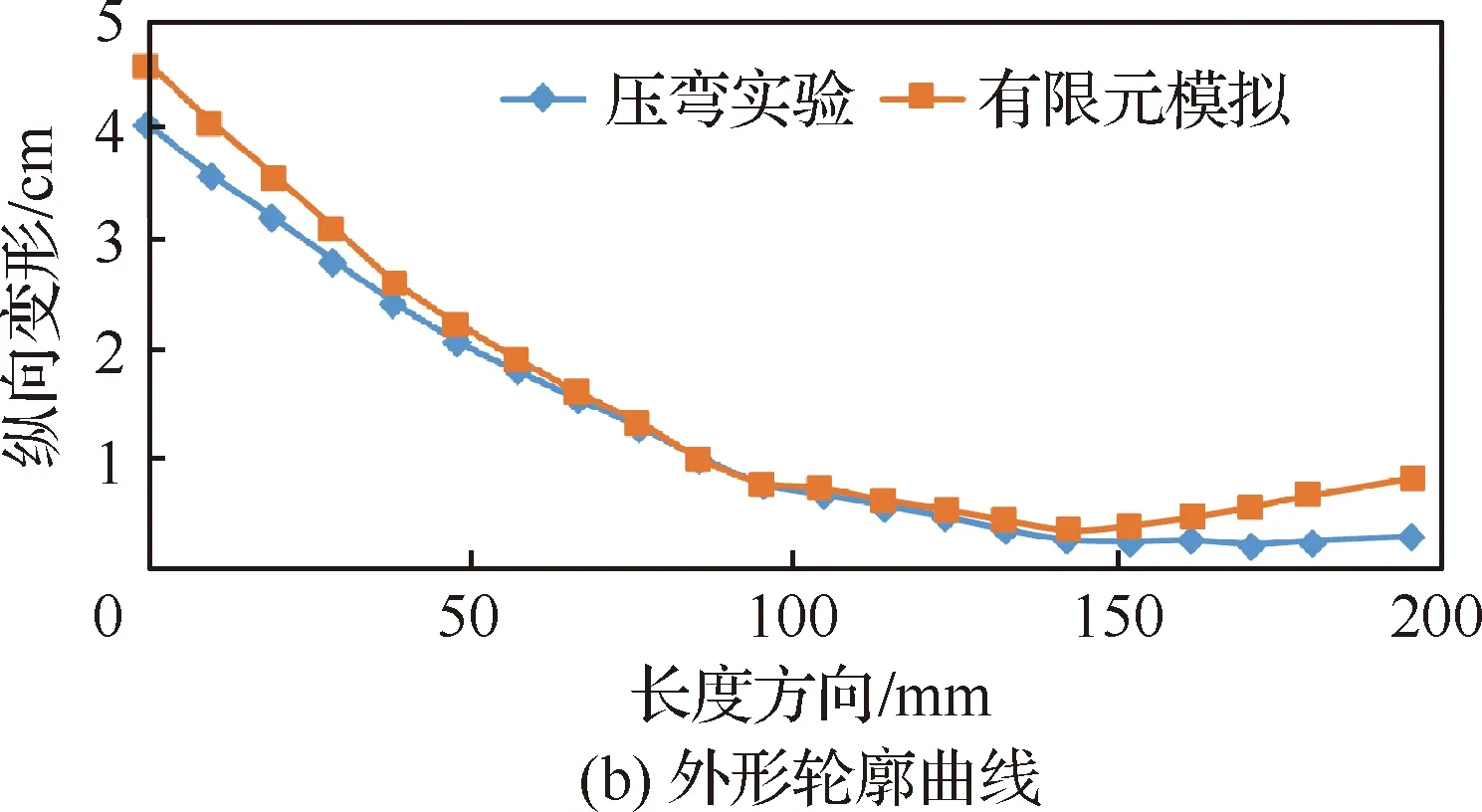
圖11 有限元模擬與壓彎實驗對比Fig.11 Comparison between finite element simulation and bending experiment

3 結果分析

構造目標曲線為半徑R=1 430 mm的圓弧[27]，如圖12(a)所示，壓點位置如圖12(b)所示，根據幾何關系，3個壓點處的初始下壓量為0.9 mm。

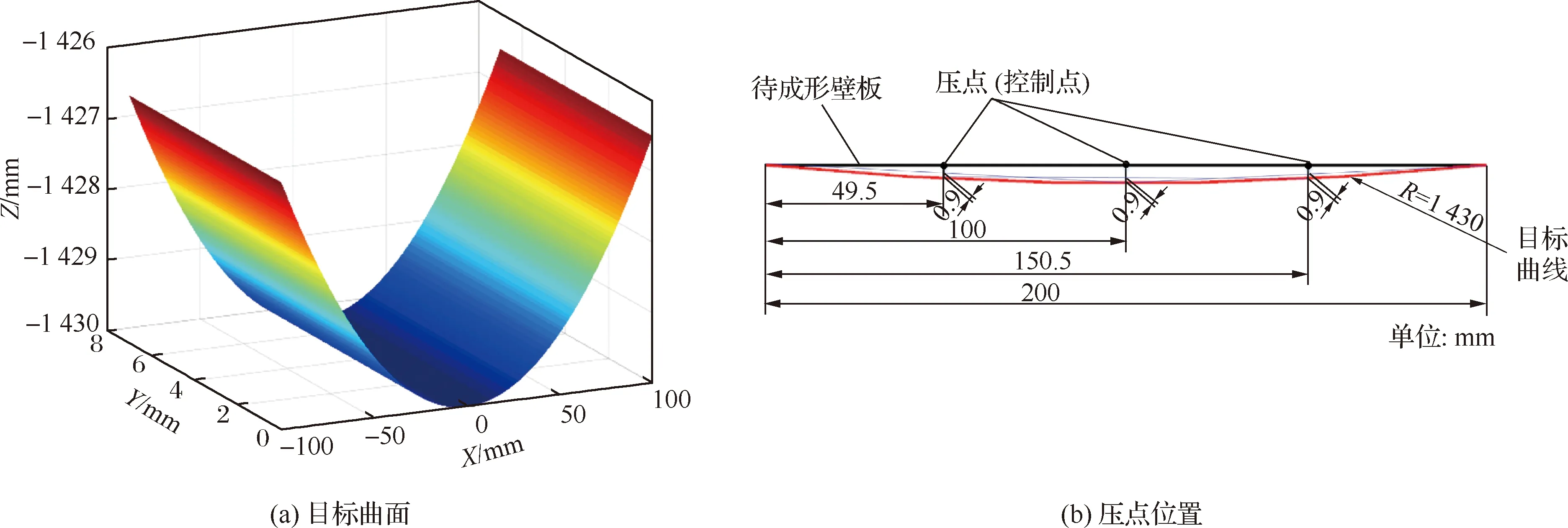
圖12 目標形狀Fig.12 Target shape

壓彎成形局部變形下壓量預測及局部-整體變形精度計算均在MATLAB中進行。根據式(10)，通過數值迭代法計算獲得目標成形曲線所需的下壓量為1.025 mm，將下壓量作為壓彎成形的初始邊界條件，按照圖3所提方法獲得目標成形曲線的迭代過程如圖13所示。由圖13(a)，補償前壓彎曲線與目標曲線最大形狀偏差為1.363 mm，整體變形誤差為0.298 mm。取補償因子為0.7，計算第1次下壓補償量為0.21 mm，補償后壓彎曲線與目標曲線之間的形狀最大偏差減小到0.021 mm，整體變形誤差為0.004 7 mm，如圖13(b) 所示。經過一次迭代成形后，壓彎成形形狀整體變形精度提高了98.4%。

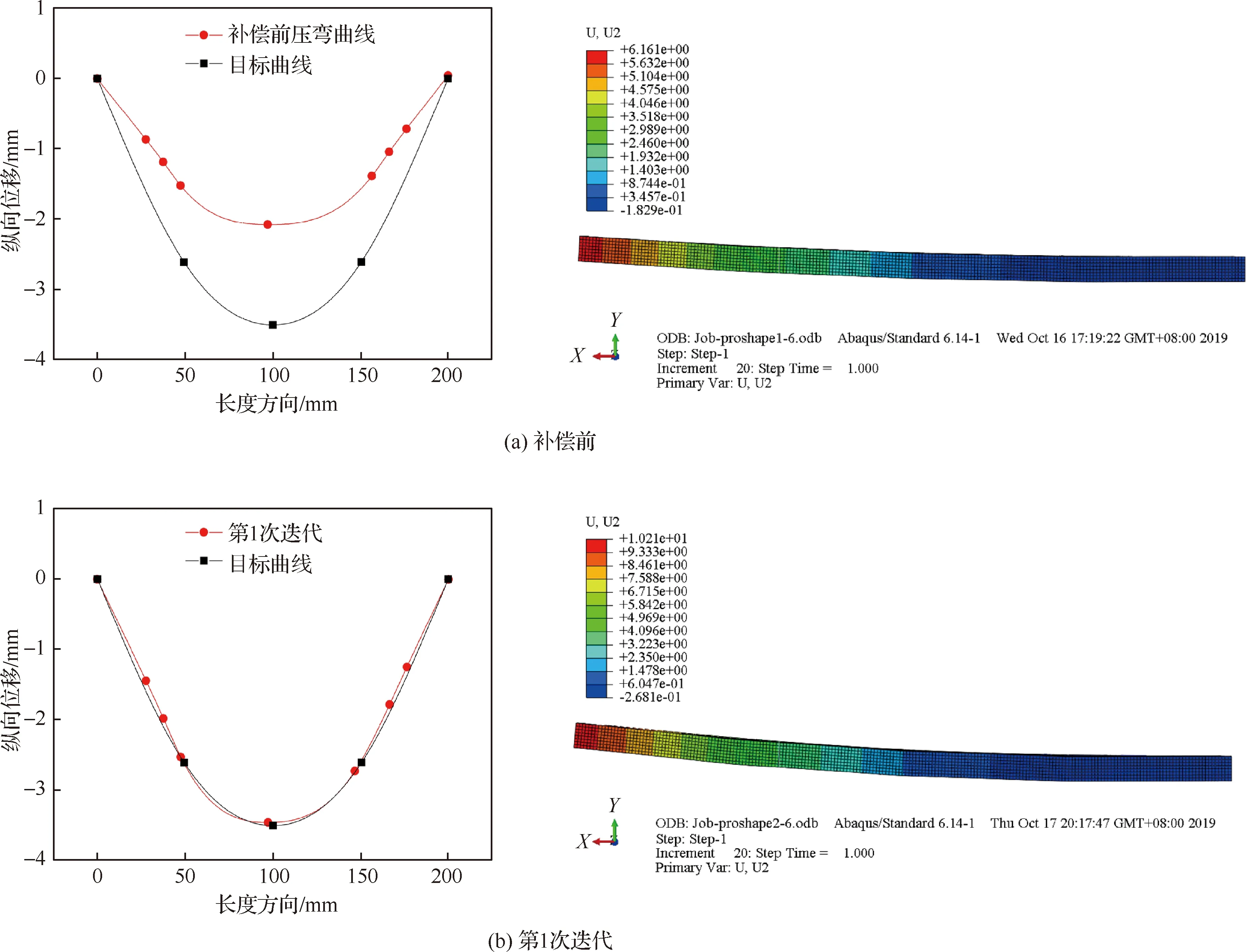
圖13 基于本文方法的成形曲線迭代過程Fig.13 Iterative process of contour curves based on the proposed method

以圖12中目標成形曲線幾何下壓量作為初始值采用試錯法進行整體壁板壓彎成形形狀控制，曲線迭代補償過程如圖14所示。圖14(a)為補償前壓彎成形后曲線，補償前壓彎曲線與目標曲線最大形狀偏差為2.133 mm，整體變形誤差為0.466 mm。選擇壓點位置作為控制點，計算控制點處與目標曲線的偏差，取補償因子為0.8，計算得到第1次迭代成形下壓補償量為0.26 mm，由圖14(b)，經過第1次補償后，壓彎曲線與目標曲線之間的形狀最大偏差減小到0.56 mm，整體變形誤差為0.122 mm。取補償因子為0.8，計算第2次迭代成形下壓補償量為0.1 mm，由圖14(c)，壓彎曲線與目標曲線之間的形狀最大偏差減小到0.139 mm，整體變形誤差為0.029 mm。經過兩次迭代成形后，壓彎成形形狀整體變形精度提高了93.5%。本文所提方法與試錯法獲得的壓彎成形整體變形誤差隨著迭代的變化過程對比如圖15所示。

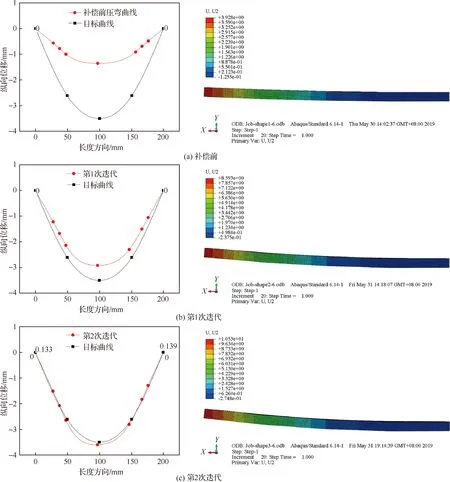
圖14 基于試錯法的成形曲線迭代過程Fig.14 Iterative process of contour curves based on trial and error method

圖15 整體變形誤差隨迭代的變化Fig.15 Evolution of global deformation error with iterations

4 結 論

1) 采用理論解析和有限元模擬相結合的方法，對整體壁板壓彎成形局部-整體變形進行預測；利用迭代補償機制與逐步逼近思想，提出了整體壁板壓彎成形的形狀控制方法。

2) 以設計的機翼整體壁板實驗樣件為例，對所提方法進行了驗證。經過一次迭代后，變形件整體變形誤差由0.298 mm降低至0.004 7 mm，壓彎成形形狀整體變形精度提高了98.4%。

3) 通過與傳統的試錯法進行對比，本文所提方法能夠以更高的精度、更快的收斂速度有效控制壓彎件的成形形狀。