結合波段相關性的FY-3C MERSI異常條帶檢測方法

閻宏波，樊憲磊，瞿瑛

(東北師范大學 地理科學學院，長春 130024)

0 引言

風云三號是我國最新一代極軌氣象衛星，可以實現對全球大氣、海洋和陸表特征參量全天候、多光譜和定量長期觀測。風云三號C星(FY-3C)作為02批的首發衛星，其核心遙感傳感器的技術指標和性能相對于01批的A/B星有了進一步的提升。FY-3C衛星搭載的中分辨率光譜成像儀(medium resolution spectral imager，MERSI)共有20個光譜波段，包括從可見光到短波紅外范圍(0.4～2.1 μm)的19個波段和1個熱紅外范圍(10～12.5 μm)波段，其中有5個250 m空間分辨率的波段和15個1 000 m空間分辨率的波段[1-2]。其光譜波段及性能指標見表1，光譜響應曲線如圖1所示。

圖1 FY-3C MERSI光譜響應函數

表1 FY-3C MERSI光譜波段及性能指標

MERSI反射率數據集是進行高精度定量反演大氣、陸地和海洋特征參量產品的基礎數據，MERSI反射率數據集存在的異常條帶會降低數據的可用性，影響基于影像數據分析結果和結論的可靠性。因此，在定量處理與分析前，需要首先對FY-3C MERSI圖像進行異常條帶檢測。通過圖像判斷和解譯發現，FY-3C MERSI 反射率數據集中存在大量的異常像元，其中異常條帶是最主要的、頻率最高的異常像元出現形式，包括異常行條帶和左側邊緣異常列條帶2種(圖2)。

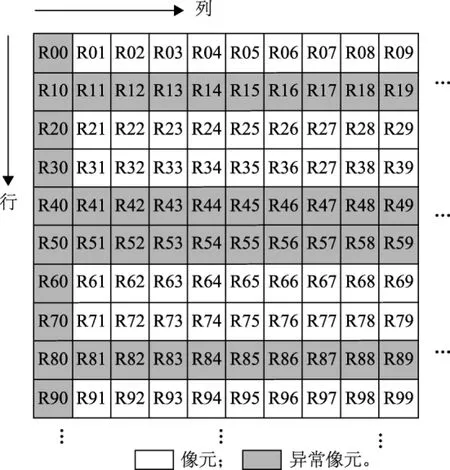
圖2 異常條帶示意圖

目前遙感圖像異常條帶檢測與去除大致可分為空間域濾波和頻率域濾波2種方法[3]。前者主要基于空間域模板和濾波算子對遙感影像的像元值進行處理[4-5]，主要包括直方圖匹配法和矩匹配法；后者將遙感影像從空間域轉換到頻率域，在頻率域選擇合適的濾波算子進行處理，最后把處理結果再轉換回到空間域，完成遙感影像的濾波處理，主要包括傅里葉變換和小波分析等方法[6-7]。這些方法雖然都可以對遙感圖像異常條帶檢測，但是其處理效果通常受到遙感影像數據和研究區特性的制約。如直方圖匹配法對遙感影像的均一性要求較高[8]，而傳統的矩匹配法對于范圍較小且地物覆蓋類型較復雜的遙感影像，處理后會產生“帶狀效應”[9-11]。基于傅里葉變換的條帶檢測方法需要在頻率域中找到合適的濾波算子對噪聲信號進行剝離。如果濾波算子不合適，則條帶噪聲檢測去除效果較差[12]。小波分析方法可以很好地剝離噪聲信號和高頻信息，但處理后的遙感影像容易出現邊緣模糊和振鈴等現象，造成遙感影像的視覺失真[13]。

在MERSI數據異常條帶檢測與去除研究中，通常使用固定閾值法和數學形態法2種方法。其中，固定閾值法是假設反射率的取值范圍在0～1之間，因此將0和1作為閾值進行異常條帶檢測，這種方法比較簡單但準確率相對較低。而數學形態法是通過構建相鄰行差矩陣，設置閾值來檢測異常條帶。該方法已經被應用于FY-3A MERSI植被指數產品異常條帶的檢測和去除[14]，取得了比較好的檢測結果。但該方法在閾值選取和定位異常行條帶位置方面缺乏普適性，并且假設異常條帶間隔均為一個掃描帶，而該假設在FY-3C MERSI數據中并不成立。因此，本研究提出了一種結合反射光譜波段相關性的FY-3C MERSI數據異常條帶檢測識別方法，基于反射率影像數據進行了驗證，并將檢測結果與數學形態法的檢測結果進行了對比分析。

1 異常條帶檢測方法

1.1 異常條帶出現規律分析

異常條帶是衛星傳感器在掃描記錄數據時，受到了信號干擾或者系統錯誤的影響，使某些遙感波段數值出現異常或缺失而導致的。通過大量影像數據解譯和判讀分析，發現FY-3C MERSI數據的異常條帶具有很強的規律性。

1)并非所有的光譜波段均存在異常條帶，而是左側邊緣異常條帶僅出現在1 000 m空間分辨率的地表反射率數據集(EV_250_Aggr.1KM_RefSB)中的第2和第4波段，且在這2個波段的異常列條帶之前的所有列的值均為0，其出現的位置為數據的前10列 (如圖3所示，其中，紅色箭頭所在列為異常列，黑色列的值為0)，而異常行條帶主要集中在數據集中的第1～4波段，其余波段雖然也存在異常行條帶，但異常像元值均為1，可以通過閾值檢測直接去除，因此在本研究中此類條帶不作為研究對象。如2014年8月15日的1景FY-3C MERSI影像，在EV_1KM_RefSB數據集中，在第6波段的第1 202、1 205、1 206、1 208和1 210行出現異常值。

圖3 部分影像第2、4波段左側邊緣列條帶

2)無論是行條帶還是列條帶均與正常行、正常列之間存在著非常明顯的分割界線，且分割界線均為水平或垂直的直線 (圖4)。

圖4 異常條帶檢測流程圖

3)與FY-3A/B MERSI數據比較，發現FY-3C MERSI 數據中不存在“Z”字形式和斜線形式的異常條帶，這主要是因為FY-3C衛星搭載的MERSI傳感器在各項性能上比FY3-A/B上搭載的MERSI有較大的提高[15]。

1.2 基于波段相關性的異常條帶檢測方法

1)波段相關性統計分析。本研究基于波段相關性，對FY-3C MERSI反射率數據集第1～4波段中存在的異常條帶進行檢測。具體思路是：分別尋找與第1～4波段反射率值相關性最好的匹配波段。通過對FY-3C MERSI圖像進行分析，發現第 1、2、4波段分別與第10、12、16波段具有很強的相關性，而第3波段與第 13和第14波段的相關性都很強，因此采用第13和第14波段的均值((波段13+波段14)/2)與第4波段匹配來建立相關關系 (表2)。本研究基于波段相關性原理，計算待檢測波段與匹配波段反射率值的差值，然后通過對行/列差值的和設置閾值，識別異常行/列條帶出現的準確位置。該算法的實施步驟是：首先對影像進行輻射定標處理；然后結合波段相關性和異常列條帶規律，分別對異常行列條帶進行檢測；最后識別出所有異常行列所在位置(圖4)。

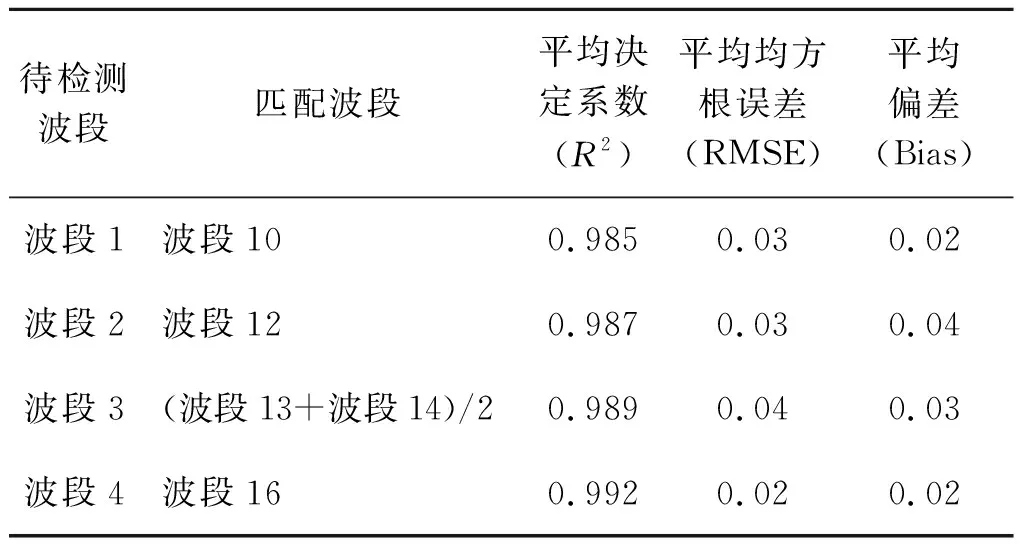
表2 波段匹配統計結果

2)輻射定標處理。為了便于后續異常條帶的檢測分析，首先對FY-3C MERSI 數據進行輻射定標，將原始DN值定標轉換為反射率值。在定標過程中，可將值為1的異常條帶直接掩膜。其中，輻射定標可以通過式(1)、式(2)實現。

DN**=slope×(DN*-intercept)

(1)

ρ=(k0+k1×DN**+k2×DN**∧2)/cosθ

(2)

式中：DN**為輻射定標值；DN*為對原始值DN經過多探元歸一化處理后的計數值；ρ表示反射率；k0、k1和k2為相應的定標系數；θ為太陽天頂角；slope和intercept為對應科學數據集中的定標斜率和截距。

3)異常行條帶檢測。對FY-3C MERSI影像中的異常行條帶的檢測算法具體步驟如下。

①定義波段差值矩陣DRow(式(3))。

DRow=Bandi-Bandj，
(i=10，12，0，16；j=1，2，3，4)

(3)

通過此矩陣構建匹配波段與對應待檢測波段的反射率之差。其中，該矩陣是一個大小與波段反射率矩陣相同的二維矩陣。

②定義一個行數為N的列向量S(式(4))。

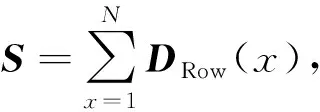
(4)

此矩陣計算DRow矩陣按行求和的結果，是一個N行的列向量，可以基于向量在下一步中確定分割閾值來識別異常行條帶。

③定義一個0，1標記矩陣FA，對不同的波段組合分別確定典型分割閾值Ti1進行二值化，見式(5)。

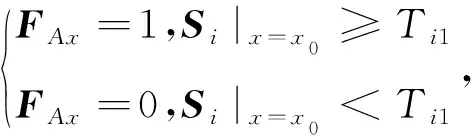
(5)

FA矩陣即為異常行的位置標記矩陣。當滿足FAx=1時的x0就是異常行所在的行號。

4)異常列條帶檢測。基于FY-3C MERSI異常行列出現規律分析可知，異常列條帶規律性更好，因此其檢測也相對簡單，其具體檢測算法步驟如下。

①定義列差值矩陣DCol，見式(6)。

DCol=|Bandi(x，y)-Bandj(x，y)|
(0≤x≤N，0≤y≤10；x，y∈N+；
i=2，4，j=12，16)

(6)

此矩陣是對波段i的反射率矩陣的前10列逐列做差并取絕對值，是一個大小為10×N二維矩陣。

②定義標記矩陣FB，見式(7)。

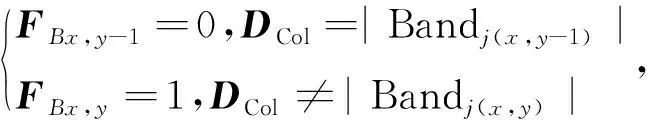
(7)

該矩陣用來判斷列差值與匹配波段對應列值是否相等，進而確定異常列條帶的列號。當FBx，y-1=0且FBx，y=1時，y值即為異常列的列號，第y列為異常列條帶。

1.3 數學形態法

目前用于檢測MERSI數據異常行條帶方法主要是數學形態法識別方法，該方法已經被廣泛應用于圖像處理。本研究將其作為對照算法，對基于波段相關性的條帶檢測方法進行評價。設為N×M的反射率影像數據矩陣，其中x，y分別代表行下標和列下標，則數學形態法的異常行條帶檢測算法實現步驟如下。

1)計算影像數據的“相鄰行差值”矩陣D，見式(8)。

D=|Rx，y+Rx+1，y|，
(0≤x≤N-1；0≤y≤M；x，y∈N+)

(8)

此矩陣的意義是，Rx，y相鄰2行的反射率值的差是一個行數為N-1、列數為M的二維矩陣，其中N+代表正整數。

2)定義一個行數為N-1、列數為M的掩膜矩陣FC，且設置閾值T2，根據式(9)進行二值化，標記每個像元的像元值是否與其同列下行的像元值存在顯著差異。

(9)

定義一個行數為N-1、列數為M的求和矩陣N，同時固定行標x=x0，0≤x≤N-1，對任意一行的有效像元值進行累加求和，如式(10)所示。

N|x=x0=∑FC|x=x0，
(Rx0，y×Rx0，y+1>0，0

(10)

3)定義一個行數為N-1、列數為1的掩膜矩陣FD，且設置閾值T3，通過式(11)進行二值化，提取出異常行的分割線標記矩陣。

(11)

在影像矩陣中，利用得到的分割線標記矩陣，將在分隔線之間的像元判斷為異常像元。

1.4 條帶檢測效果評價與比較

選取2014年FY-3C MERSI數據的67景影像(數據獲取于風云衛星遙感數據服務網http：//satellite.nsmc.org.cn)作為實驗數據，分別對影像數據采用本文提出的基于波段相關性的行列條帶檢測方法和數學形態法，進行異常行列條帶檢測。將自動檢測結果與目視判讀進行比較，統計檢測出的異常行數、準確率和漏檢率，對算法的檢測效果進行綜合評價。

2 結果與討論

基于67景FY-3C MESRI影像數據進行條帶檢測實驗，其中圖像數據共有155條異常行條帶，134條異常列條帶。基于本文算法可以檢測出152條異常行條帶，檢測率為98.1%，誤檢率為0，漏檢率為1.9%，并且可以檢測出所有的列異常條帶(列檢測率為100.0%)；而采用數學形態法僅能檢測出100條異常行條帶，檢測率為64.5%，誤檢率為45.2%，漏檢率為35.5%，如表3、表4所示。圖5展示了基于本文算法和數學形態法對FY-3C MERSI影像進行異常條帶檢測的一些典型案例，其中圖5(a)、圖5 (b)顯示對于第1波段，2種方法均能很好地將異常行條帶檢測出來；圖5(c)、圖5 (d)顯示對于第2波段，數學形態法漏檢了1行，其中黃色箭頭所在行即為未能正確檢測出來的異常行條帶；圖5(e)、圖5 (f)顯示對于第3波段，數學形態法不僅未能正確檢測出異常行條帶，反而誤檢了1行，其中紅色箭頭所在位置為誤檢行，黃色與綠色箭頭指示了漏檢的異常行條帶；圖5(g)、圖5 (h)顯示對于第4波段，數學形態法誤檢了1行，其中黃色箭頭為誤檢的異常行條帶。

表3 行條帶檢測結果

表4 列條帶檢測結果

通過表3、表4和圖5可以發現，基于數學形態法進行FY-3C MERSI數據條帶檢測，存在比較嚴重的誤檢和漏檢等問題，其中誤檢率高達45.2%，漏檢率也有35.5%。造成這些問題的原因主要有2個：首先數學形態法是在同一波段數據中逐行做差，因此基于這種方法不能使異常條帶處差值與正常行處的差值形成明顯的差距，特別是在異常行與相鄰行差異不明顯的地方更是如此，這就很難確定一個具有普適性的分割閾值來批量處理影像數據，并且第2個閾值還受到第1個閾值的影響，使其普適性大大降低；其次數學形態法最終檢測出的是正常行和異常行之間的分割界線，理論上分割界線之間的就是異常行，但是如何確定分割界線的起止位置是一個難點。研究發現，相鄰分割界線之前的行數并不都是一個掃描帶的寬度，因此盡管找到了異常行與正常行之間的分割界線，但是要準確確定異常行位置仍然相對困難。

圖5 行檢測結果對比圖

本文提出的算法本質上只需要確定一個閾值，并且正常值與異常值區分度較大，容易確定普適性強的閾值。此外，本文算法最終直接標記的是異常行、列所在的行、列號，而非分割界線，這就避開了確定的分割界線起止順序的難點。但是在實驗中發現，無論是數學形態法還是本文算法，對于極少出現的斷續條帶(即在影像一行中，只有若干異常像元，而剩余像元均為正常像元的情況)，均無法正確進行檢測，這需要在研究中根據圖像特點設置更為復雜的閾值判斷規則才能夠加以解決。

3 結束語

本研究提出了一種結合波段相關性的FY-3C MERSI數據異常條帶檢測方法，基于反射光譜波段之間的相關關系，構建波段差矩陣，最終檢測出異常行列條帶所在位置。基于67景FY-3C MERSI數據的條帶檢測實驗表明，本文算法適用于大批量檢測FY-3C MERSI數據異常條帶，顯著高于數學形態法的檢測率，無誤檢條帶，大大降低了誤檢率和漏檢率，為風云系列衛星反射率數據集進一步的應用研究奠定良好的基礎。