有效開展數學結構化學習

施麗

【關鍵詞】數學結構化學習；《認識一個整體的幾分之一》；知識結構；模塊結構；練習結構

【中圖分類號】G623.5【文獻標志碼】A【文章編號】1005-6009（2020）41-0065-04

美國教育家布魯納認為：“學習一門學科，就是要掌握這門學科的基本結構。”數學常被稱為“結構的科學”，它的學科知識之間有著千絲萬縷的關聯。數學結構化學習，是指建立在數學知識系統和學生已有認知的基礎上，以動態建構為核心，以整體關聯為抓手，以思維發展為方向，以數學素養培育為目標追求的學習過程、學習方式和方法。在數學教學中倡導結構化學習，有助于學生將新獲取的個別的、無規律的、零散的知識進行分析、篩選、歸納后納入自己原有的數學知識網絡中，最終在頭腦中形成更加完善的認知結構。在開展數學結構化學習時，要注意突出整體性、關聯性、系統性，站在整體、聯系、系統的高度把握和處理教材，引導學生充分把握和感受數學的知識結構，體驗數學知識的形成、發展和運用過程。下面，筆者以蘇教版三下《認識一個整體的幾分之一》一課的教學為例，談談如何有效開展數學結構化學習。

一、依據知識結構，讓課堂從“線性”走向“網狀”

“線性”的課堂以教學內容的邏輯為依據，以主要問題為連接點，以提出問題、分析問題和解決問題為基本操作手段，整個教學過程仿佛連成了一條由一個個具有嚴格間距的教學環節所構成的直線一般，雖然操作上嚴密且易把握，但是一旦教師“圈”得過牢，“把”得過多，課堂就易變得亦步亦趨，最終可能導致學習空間的窄化和學生思維的僵化。在“網狀”的課堂中，教師以聯系的觀點組織教材，以發展的手段設計教學過程，引導學生將獲取的“線性”知識結構進行整理，重組到自己的知識網絡中，讓知識元素有機聯系。數學結構化學習讓課堂從“線性”走向“網狀”，要求教師從知識結構入手，立足整體，統攬全局，擺脫課時束縛，把握知識之間的內在關聯，促進知識的融合和溝通，讓學生知一節聯一片。如在導入環節，教師遵循知識的序列化，注重知識網絡框架的搭建，以故事切入，復習了三上“認識分數”的內容，并強調分數與份數有關，為接下來的新知學習做鋪墊。

師：有一個叫花果山的地方，山上有許多猴子。正逢收獲的季節，猴王正在給小猴們分山果呢，瞧！猴王給兩只小猴帶來了什么呀？（一個桃）

師：兩只小猴，一個桃，怎么分？

生：平均分。

師：那在圖上可以怎么表示平均分呢？

生：用虛線從中間分開。

師：真好！把1個桃平均分給2只小猴，每只小猴能分得這個桃的幾分之幾呢？

生：每只小猴能分得這個桃的二分之一。

師（指名解釋二分之一后）：真厲害！每只小猴分得半個桃，大家想到用分數二分之一來表示，還關注到分母2表示2份和分子1表示1份，也就是說分數與份數有關（板書“份數”）。

二、生成模塊結構，讓教學從“個別”走向“整體”

按部就班地教學局部知識是一種個別性的教學行為方式，不利于學生獲得完整的知識體系，也會使學生學習遷移能力的培養效果大打折扣。數學結構化學習呈現出從個別性走向整體性的趨勢。它要求教師聚焦模塊教學，大膽優化教學內容，讓學生學一塊通一類。本節課中，“辨析模塊”“探究模塊”和“完善模塊”這三個教學模塊始終圍繞“分數與份數直接相關，與數量無關”的主題，展開充分的辨析、自主的探究和實踐的完善與總結，讓知識的深度得以凸顯。

“辨析模塊”初識二分之一的知識，受物體個數的影響，學生很容易出錯，教師直面普遍問題，給學生提供討論的空間，引導他們在不斷質疑和討論中關注“整體”。

師：把一盤桃（6個）平均分給2只小猴，每只小猴分得這盤桃的幾分之幾？請在小組內充分討論后再匯報。

生1：我認為是六分之三，因為一共有6個桃子，每只小猴分得了3個。

生2：我認為是二分之一，因為是把一盤桃平均分成2份，每只小猴分得了其中的1份。

生3：我認為六分之三和二分之一都可以。

師：我聽明白了，認為是六分之三的同學，你們的意思是每只小猴分得3個，而認為是二分之一的同學，你們的意思是每只小猴分得1份，是吧？看來咱們的分歧就出在份數與個數上。同學們，沒關系，在學習道路上遇到新問題時，咱們不妨退到一開始而又不失去重要性的地方去重新思考，也就是分數與何有關聯（指著板書“份數”），現在你覺得到底哪個分數更合適呢？

生：二分之一。

師：認為是六分之三的同學還堅持嗎？（生搖頭）為什么不堅持了？

生：因為黑板上二分之一不是指2個桃子，而是指平均分成2份，那六分之三就應該是平均分成6份，這里是平均分成了2份，所以是二分之一才對。

“探究模塊”深入認識二分之一的知識，教師引導學生自主畫一畫、分一分，并結合對比各種畫法與分法的相同點與不同點，使他們從整體上關注到平均分與桃子的數量沒有直接關系，從而加深對二分之一的理解，不斷完善認知結構，發展思維能力。

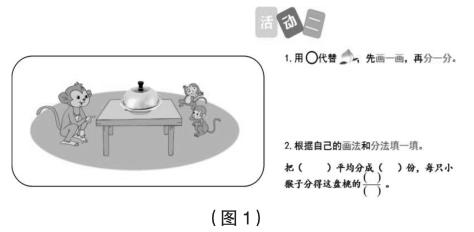
師：這一盤桃，大家會分了，可淘氣的猴王又準備了一盤桃，不知道有多少個，仍然平均分給2只小猴，每只小猴又能分得這盤桃的幾分之幾呢？在學習單（如下頁圖1）上畫一畫、分一分，并根據自己的畫法填一填。

生匯報：把4個桃平均分成2份，每只小猴分得這盤桃的二分之一；把8個桃平均分成2份，每只小猴分得這盤桃的二分之一；把3個桃平均分成2份，每只小猴分得這盤桃的二分之一……

師：同學們真厲害，想到了這么多種畫法，咱們來仔細看看這些畫法和分法，有什么相同的地方呢？

生：無論哪種分法，每只小猴都分得這盤桃的二分之一。

師：真愛觀察！它們又有什么不同呢？

生：每盤桃個數不同，每份桃個數也不同。

師：這就奇怪了，每盤桃個數不同，每份桃個數也不同，為什么都能用二分之一表示呢？

生：因為都是平均分給2只小猴，每只小猴分得2份中的1份。

師：真了不起！4個、6個、8個甚至更多桃，我們都看成一盤桃，只要把一盤桃平均分成2份，每份就是這盤桃的二分之一。

“完善模塊”認識三分之一的知識，與上述兩個模塊一起，讓學生在環環相扣的活動中完善和提升，讓教學逐步走向整體。

師：聽到有桃分著吃的消息后，又來了一只小猴。想一想，這時猴王會怎樣分這盤桃？如果把一盤桃平均分成3份，每份是這盤桃的幾分之幾？

生：三分之一。不管有多少個桃，把一盤桃平均分成幾份，每份就是它的幾分之一。

三、拓展練習結構，讓思維由“單一”走向“多元”

數學結構化學習能促進學生的思維由單一化走向多元化，這一點尤其體現在數學課堂練習上。教師應輕于題海戰術，重于題質推敲，探索對比變式性題組練習，讓學生練一組長一技。本節課的鞏固練習是在教材的基礎上進行變式重組的，將“一個物體”和“一個整體”進行直觀對比分析，使學生在題組練習中清楚地掌握了分數的內涵，最終理解了“一個整體”的本質，為學生從單一認知到多元思維創造了更加有利的條件。

出示練習題：數一數，比一比，用數表示涂色部分。（逐步出示圖2中的各個元素）

師：同學們真厲害！對“一個整體”的認識真深刻！

總之，要有效實現數學結構化學習，需要教師在正確解讀新課程理念的基礎上，多維度地為學生創設條件，讓學生在學習中形成良好的認知結構，讓數學學習深度發生。

【參考文獻】

[1]陳學勤.遮一遮，本質更明——“認識一個整體的幾分之一”教學片斷與思考[J].小學數學教師，2018（2）：71-74.

[2]黃麗紅.小學數學“模塊教學、整體建構”的探索與實踐[J].小學數學教育，2018（11）： 7-9.

[3]許衛兵.結構化讓學習深度發生——結構化學習：回歸“本原”的課堂實踐[J].小學數學教師，2018（7）：64-70.

（作者單位：南京市江寧上坊新城小學）