關于三角形的一個不等式鏈

時 軍 蘇化明

(合肥工業大學數學學院 230009)

本文給出一個關于三角形的不等式鏈，即如下的:

定理設△ABC的半周長為p，面積為Δ，外接圓半徑為R，內切圓半徑為r，則有

(1)

其中所有的等號當且僅當△ABC為正三角形時成立.

首先介紹如下的引理.

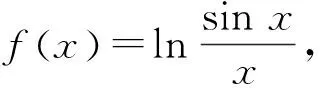
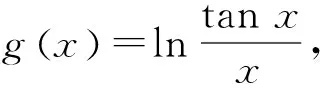
引理的證明由f(x)=ln sinx-lnx，知

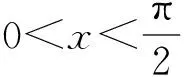
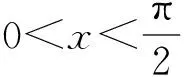
f(x)為上凸函數.

由g(x)=ln tanx-lnx知

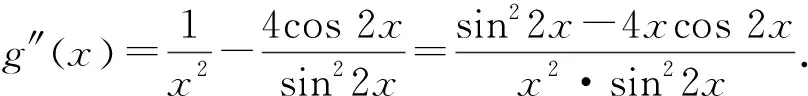
g″(x)>0.

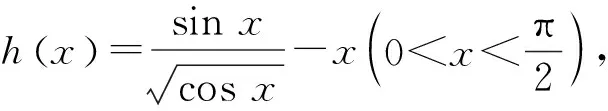
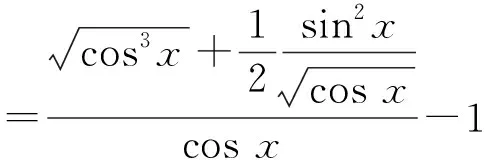
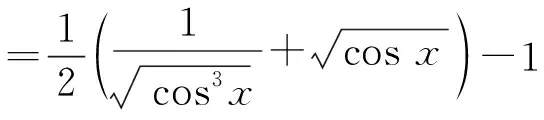
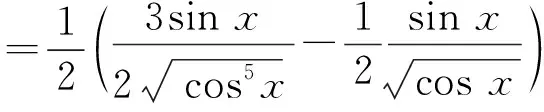
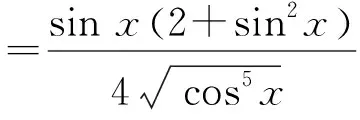
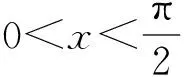
(2)

sin22x-4x2cos 2x>0，

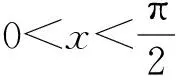
注： ① 不等式(2)等價于

(3)

② 不等式(2)可加強為[1]

(4)

下面進行定理的證明:

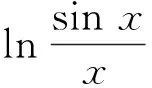
由此知

再由△ABC中的等式

可得

(5)

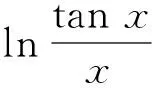
故由Jensen不等式知

由此知

或

利用△ABC中的等式

可得

(6)

由算術—幾何平均不等式知

sinA+sinB+sinC

利用△ABC中的等式

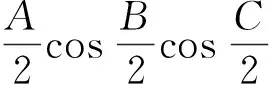
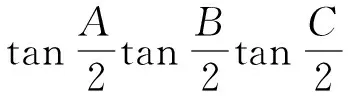
再由△ABC中的等式

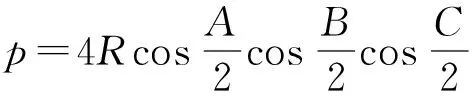
或

(7)

由此知

利用△ABC中的等式

可得

(8)

由算術—幾何平均不等式知

由此知

(9)

由式(5)，(6)，(7)，(8)，(9)知不等式(1)成立.由于(5)—(9)中等號均為當且僅當△ABC為正三角形時成立，故(1)中所有的等號當且僅當△ABC為正三角形時成立.

最后指出，△ABC中有著名的Euler不等式[1]：R≥2r，而不等式(1)對此不等式進行了若干隔離或加細.