基于不完美CSI的異構NOMA網絡能效優化算法

徐勇軍，謝豪，陳前斌，林金朝，劉期烈

（1.重慶郵電大學通信與信息工程學院，重慶 400065；2.移動通信技術重慶市重點實驗室，重慶 400065）

1 引言

手機、電腦等智能設備數量的快速增長導致網絡數據量越來越大，下一代無線通信系統在系統容量方面將面臨嚴峻挑戰[1]。異構網絡可以提高系統的吞吐量和覆蓋率，解決小區邊緣用戶資源分配不均，因此受到廣泛關注[2]。異構網絡由傳統的宏基站和許多小型基站組成[3-5]，在該網絡中跨層干擾、資源分配將面臨很大的挑戰[6]。

從另一個層面講，由于頻譜資源越來越稀缺，因此非正交多址接入（NOMA,non-orthogonal multiple access）技術被提出并用于解決頻譜資源稀缺問題。由于高頻譜效率和高系統容量的特點，NOMA 技術被認為是未來通信系統中有前景的一種技術[7-9]。NOMA 不同于傳統的正交多址接入，它允許多個用戶在同一個頻段上以不同的功率等級復用頻譜資源，在發送端使用疊加編碼信號，并主動引入干擾信息，在接收端使用串行干擾消除（SIC,successive interference cancellation）技術實現正確的解調。因此，基于NOMA 異構網絡的相關研究具有重要意義。

近年來，針對NOMA 異構網絡，大量學者主要從吞吐量最大和能量效率最大的角度進行研究。在吞吐量最大方面，文獻[10]研究了完美信道狀態信息下的單蜂窩NOMA 網絡的下行鏈路，利用匹配理論對其進行資源優化，即匹配用戶對中的2 個用戶可以通過共享相同的頻譜來提高系統吞吐量。文獻[11]研究了一種基于全雙工NOMA 系統的聯合子載波和功率分配問題，提出了一種近似于最優性能的次優迭代方案來提高系統吞吐量。文獻[12]提出了一種基于Stackelberg 博弈的分布式功率分配方法，針對單蜂窩異構NOMA 網絡，在每個用戶的最小數據速率約束下最大化系統吞吐量。在基于NOMA 的異構認知網絡中，采用了交織式頻譜共享的方法，并且通過聯合優化帶寬分配和功率分配來最大化小蜂窩的總吞吐量[13]。上述工作都是研究吞吐量最大化的問題，忽略了系統的功率消耗問題。文獻[14]通過優化子信道分配和功率分配來最大化NOMA 網絡下行傳輸鏈路的能量效率，并提出了一種新的跨子信道功率分配算法進一步提高能量效率。在異構NOMA 網絡中通過子信道分配和功率分配最大化整個系統的能量效率（包含宏蜂窩和小蜂窩），考慮了同層干擾與跨層干擾，并提出了一種次優的資源分配算法[15]。

上述工作大部分是基于完美信道狀態信息，缺乏對不完美信道狀態信息的討論。實際應用中受物理信道的估計誤差、反饋時延和量化誤差的影響，很難獲取真實的信道狀態信息。在不完美信道狀態信息條件下，文獻[16]對用戶調度和功率分配進行了迭代優化，使系統的能效最大化，并證明了所提用戶調度和功率分配方案優于正交多址接入方案，然而其研究的是單蜂窩網絡，現實中往往是多用戶多蜂窩網絡，同時實際系統的參數估計誤差不一定服從高斯分布。因此，研究多用戶多蜂窩網絡下的穩健資源分配具有重要意義。

本文研究基于NOMA 異構網絡穩健資源分配算法，以多用戶多蜂窩網絡為系統模型，最大化系統能效。主要貢獻如下。

1) 建立了一個基于多用戶多蜂窩的NOMA 異構網絡模型。考慮了小蜂窩基站功率約束、宏用戶跨層干擾功率約束、資源塊分配約束及小蜂窩用戶服務質量約束，建立了整個小蜂窩總能效最大化的資源優化問題。該資源優化問題是一個混合整數非線性分式規劃問題，不易獲得解析解。

2) 為了實現頻譜共享和保證用戶的服務質量，在原模型中引入隨機信道不確定性參數。基于橢球不確定模型，使原問題變成無限維優化問題。利用松弛變量將離散的資源塊分配變成一個連續優化問題；基于最壞準則原理將含不確定性參數的約束條件轉化為確定性的凸約束；利用Dinkelbach 法[17]將分式目標函數轉化為相減形式，并通過連續凸近似方法將原問題轉化為凸問題，利用拉格朗日對偶原理及次梯度更新算法來得到解析解。

3) 仿真結果表明，與非穩健算法相比，本文算法具有較好的收斂性、能量效率及攝動抑制能力。

2 系統模型及問題描述

本文考慮一個多蜂窩多用戶NOMA 異構網絡。M個宏用戶通過上行傳輸的方式與宏基站進行數據傳輸，小蜂窩基站通過下行傳輸的方式向小蜂窩用戶傳輸數據。系統模型如圖1 所示。

圖1 系統模型

系統中有一個宏蜂窩網絡和N個小蜂窩網絡。假設每一個用戶和基站都配備單根天線，每一個小蜂窩用戶在一個時隙上只能連接一個小蜂窩基站，但每個小蜂窩基站能夠同時服務多個小蜂窩用戶，并且多個小蜂窩數據能在同一信道上傳輸。假設每個資源塊都是單位帶寬，且由于低功率和很強的穿墻損耗的特點，不同小蜂窩之間的相互干擾可以忽略[15]。宏蜂窩網絡中有N個小蜂窩網絡，每個小蜂窩基站服務U個小蜂窩用戶，其中?n∈N={1,2,…,N},?i,j∈U={1,2,…,U}，并定義宏用戶集合為?m∈M={1,2,…,M}。假設有K個資源塊，定義資源塊集合為 K={1,2,…,K},?k∈K。每個資源塊只能被一個宏用戶使用，但是基于NOMA 協議，多個小蜂窩用戶可以占用同一資源塊，其中小蜂窩基站和小蜂窩用戶使用了疊加編碼和SIC 技術。宏用戶和小蜂窩用戶可以通過共享頻譜來提高頻譜效率和整個小蜂窩的吞吐量。假設系統為塊衰落信道，則信道增益在同一個資源塊里面是一個常數，但是在不同的信道里面會有變化[15]。系統參數及其含義如表1 所示。

表1 系統參數

基于下行鏈路功率域NOMA 準則，對于任意的j＞i,第j個小蜂窩用戶能夠解碼第i個小蜂窩用戶的信號并且能夠將其從自己的信號中消除，但是對于任意j＜l，第l個小蜂窩用戶的信號將會被第j個小蜂窩用戶視為干擾。根據香農公式，在第n個小蜂窩里的第i個小蜂窩用戶通過第k個資源塊的傳輸速率為

其中，有

式(2)中分母的第一項表示來自其他小蜂窩用戶的蜂窩內干擾，第二項表示來自宏蜂窩用戶發射機的跨層干擾，第三項δ2表示均值為零的加性高斯白噪聲。

本文的目標是在小蜂窩用戶的QoS 約束、資源塊分配約束、小蜂窩基站的最大發射功率約束及宏用戶的跨層干擾約束下，最大化所有小蜂窩用戶的能效。因此，在完美信道狀態信息下，這個目標可以通過聯合優化發射功率和資源塊分配因子來表示，如式(3)所示。

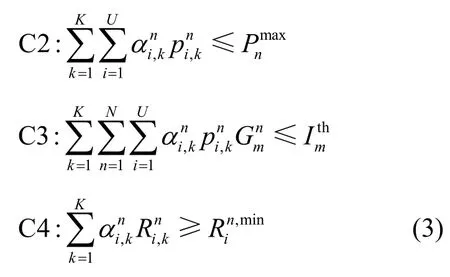
其中，C1表示資源塊分配因子約束條件，保證每個資源塊只分配給一個小蜂窩；C2 表示第n個小蜂窩基站的最大發射功率約束；C3 和C4 保證每個用戶的QoS，C3 表示所有小蜂窩基站對第m個宏蜂窩用戶的跨層干擾約束條件，C4 表示第n個小蜂窩中的第i個小蜂窩用戶的最小速率約束條件。

3 穩健資源分配

由于約束條件C1，優化問題P1 是一個混合整數非線性分式規劃問題，它的全局最優解很難獲得。資源塊分配因子是個離散的變量，因此使用凸松弛法將變量松弛為一個[0,1]中的連續實數變量。由于∈[0,1]，可以將其考慮為對于資源塊k的一個時間共享因子，這意味著在一個塊傳輸時間內第n個小蜂窩中第i個小蜂窩用戶占用資源塊k的時間比例，另外，為了簡化符號，引入輔助變量。因此，P1 優化問題可以重新表述為P2，如式(4)所示。

為了克服不確定性的影響，優化問題P2 考慮了信道的不確定性。P2 中的信道不確定性存在于以下幾個方面：小蜂窩基站到小蜂窩用戶之間的鏈路、小蜂窩基站對宏蜂窩用戶的干擾鏈路、宏蜂窩用戶發射機對小蜂窩用戶的干擾鏈路。因此可以得到優化問題P3，如式(5)所示。

其中，約束條件C5 包含了不確定參數集合，?h代表小蜂窩用戶和小蜂窩基站之間鏈路的信道不確定性集合，?g表示宏蜂窩用戶發射機和小蜂窩用戶之間鏈路的信道不確定性集合，?G表示小蜂窩基站和宏蜂窩用戶之間的信道不確定性集合。

3.1 跨層干擾中的信道不確定性

根據穩健優化理論，考慮有界信道誤差，將小蜂窩基站和宏蜂窩用戶之間的信道不確定性用橢球有界不確定性集合來表示，如式(6)所示。

其中，?G的大小取決于信道估計的準確度，?G的形狀取決于誤差源，比如高斯噪聲、信道反饋時延、多普勒頻移、量化誤差，| ?|表示絕對值，εm≥ 0表示誤差上界，分別表示信道估計值和對應的估計誤差。

穩健優化理論是處理穩健約束的著名理論，基于最壞準則，在最壞不確定性情況下，約束能夠得到保證，即最大化最壞估計誤差。根據Cauchy-Schwartz不等式，可得

3.2 傳輸速率中的信道不確定性

為了保證每一個小蜂窩用戶基本的QoS 要求，要考慮小蜂窩用戶最小傳輸速率約束中的不確定參數。同樣地，小蜂窩用戶和小蜂窩基站之間的信道不確定性、宏蜂窩用戶發射機到小蜂窩用戶之間的信道不確定性分別用有界不確定性集合?h和?g來表示，如式(9)和式(10)所示。

同樣地，約束條件C4 等價于式(11)。

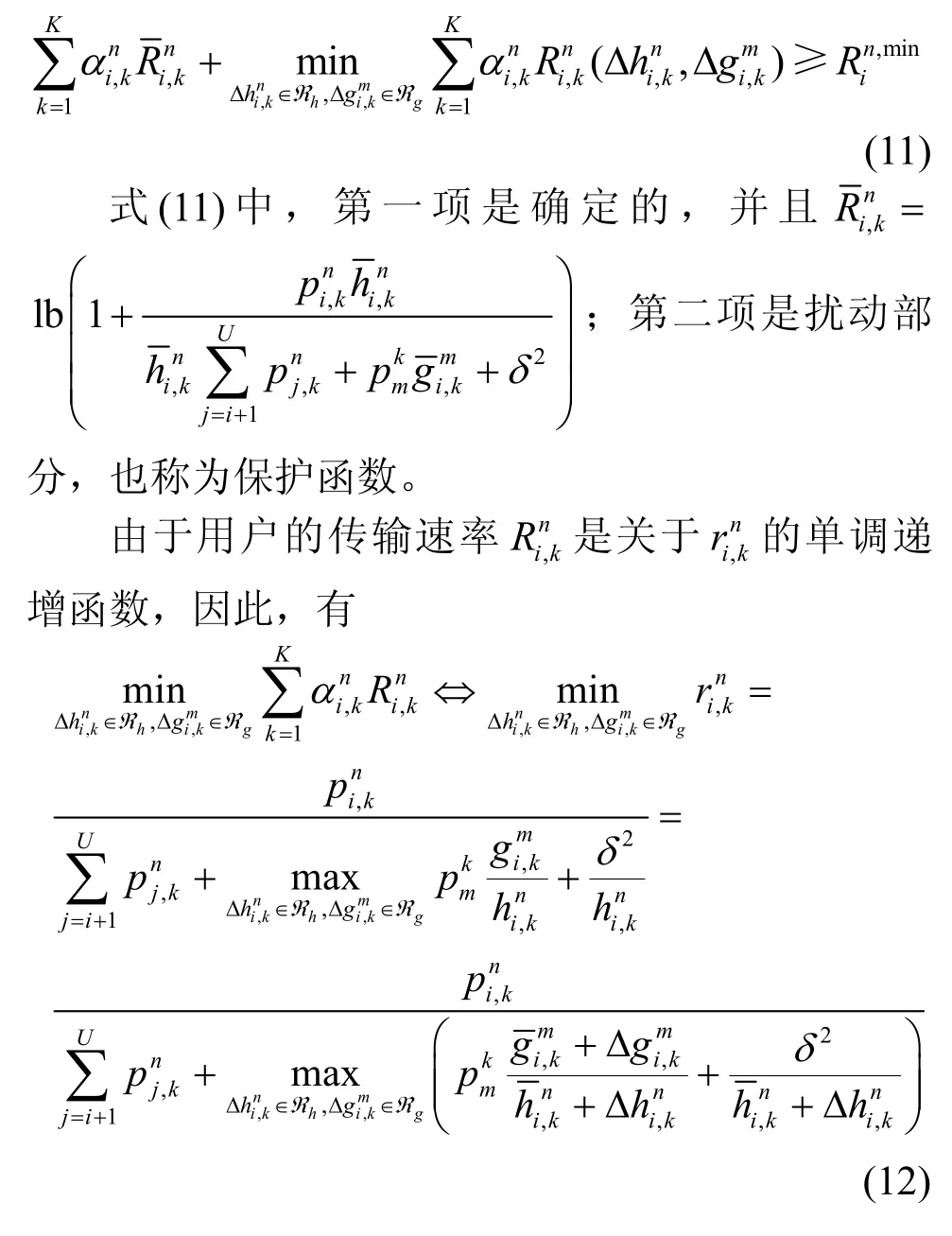
因此，優化問題P3 可以重新表述為P4，如式(17)所示。

優化問題P4 是一個非線性分式規劃問題，很難獲得它的全局最優解。因此，基于Dinkelbach 法，分式規劃問題可以改寫成式(18)形式。

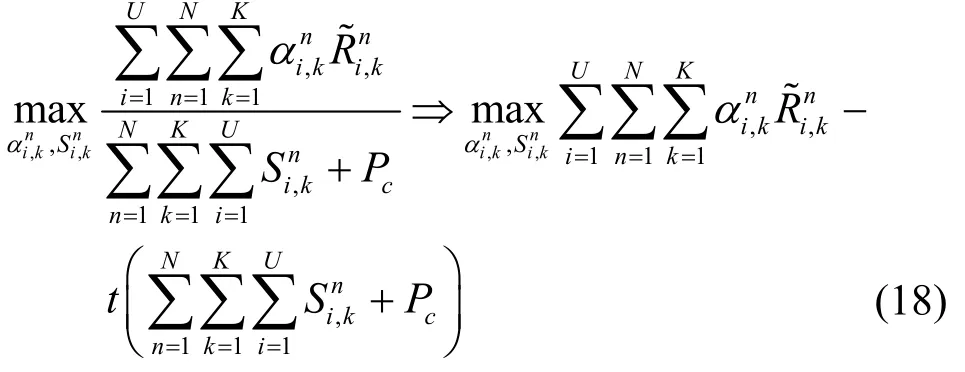
其中，t≥0 為輔助變量，表示整個小蜂窩網絡的總能量效率。因此，可以定義

從式(19)中可以看到，當t趨于正無窮時，f(t)是負數；當t趨于負無窮時，f(t) 是正數。因此，可以證明f(t) 是關于t的凸函數，并且是關于t嚴格遞減函數。定義分別表示該問題的最優資源塊分配因子和最優分配功率，因此，當且僅當式(20)成立時，能夠實現最大能效t?。

其中，所有小蜂窩的最大能效t?可表示為

因此，優化問題P4 可以轉換為式(22)所示的優化問題P5。

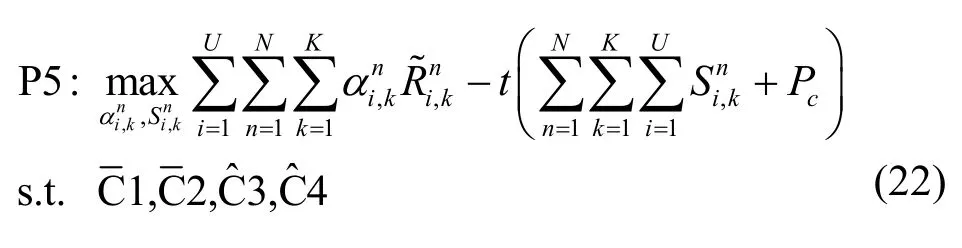
為了解決優化問題P5，本文使用連續凸近似法將優化問題P5 轉化成凸優化問題，利用下界迭代來得到最優解，如式(23)所示。

其中，α和θ分別為

當Q=Q0時，式(23)的等號成立。首先，定義為

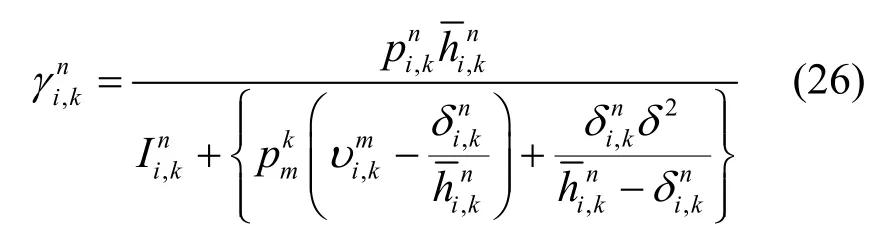
因此，數據速率可以近似為

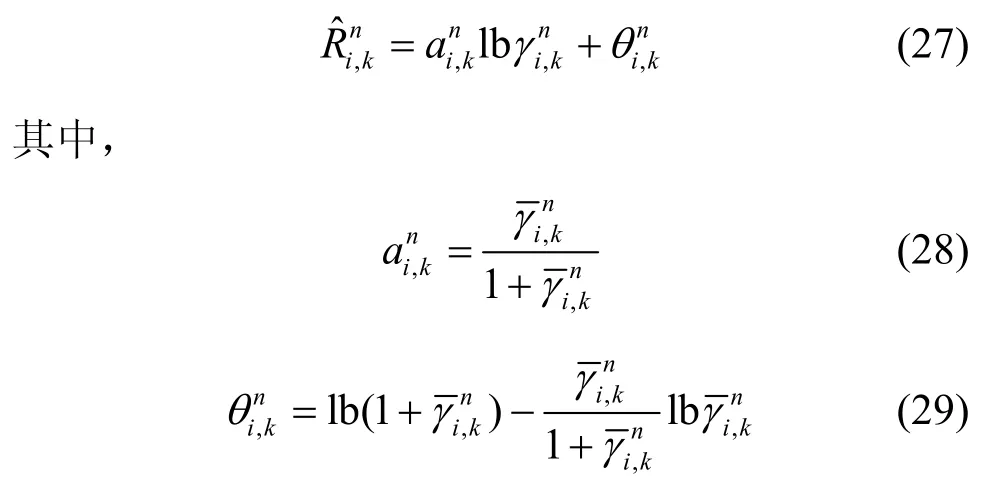
優化問題P6 是一個確定的凸優化問題，有唯一的最優解，因此可以通過拉格朗日對偶法解決。

3.3 穩健資源分配算法求解

優化問題P6 的拉格朗日函數如式(31)所示。

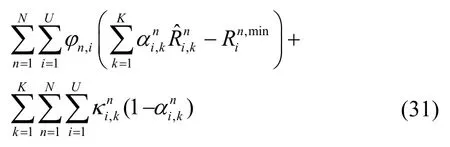
其中，λn≥ 0，φm≥ 0，?n,i≥ 0，≥ 0表示優化問題P6 約束條件所對應的拉格朗日乘子。因此，拉格朗日函數可以描述為

優化問題P6 的對偶問題為

根據KKT（Karush-Kuhn-Tucker）[18]條件，最優分配功率求解為

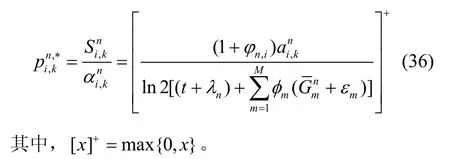
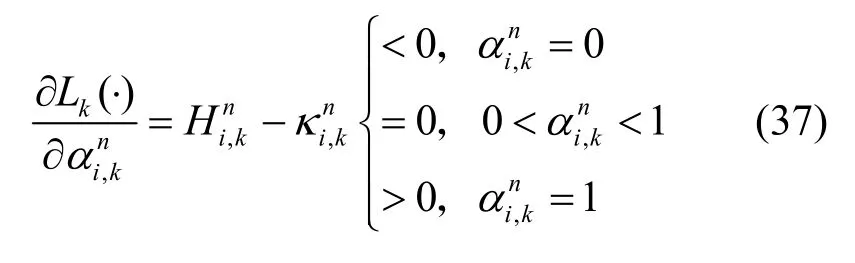
其中，

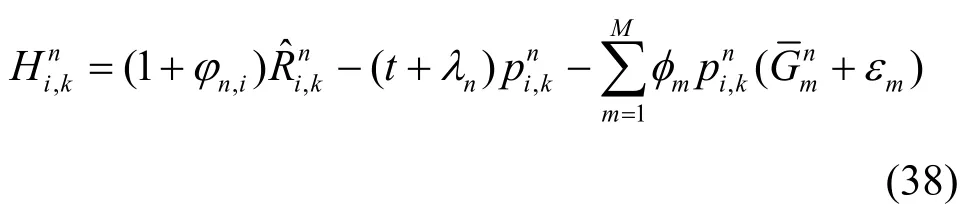
因此，第k個資源塊總是分配給最大的第n個小蜂窩基站中第i個小蜂窩用戶，即

采用次梯度法更新拉格朗日乘子，如式(40)～式(43)所示。

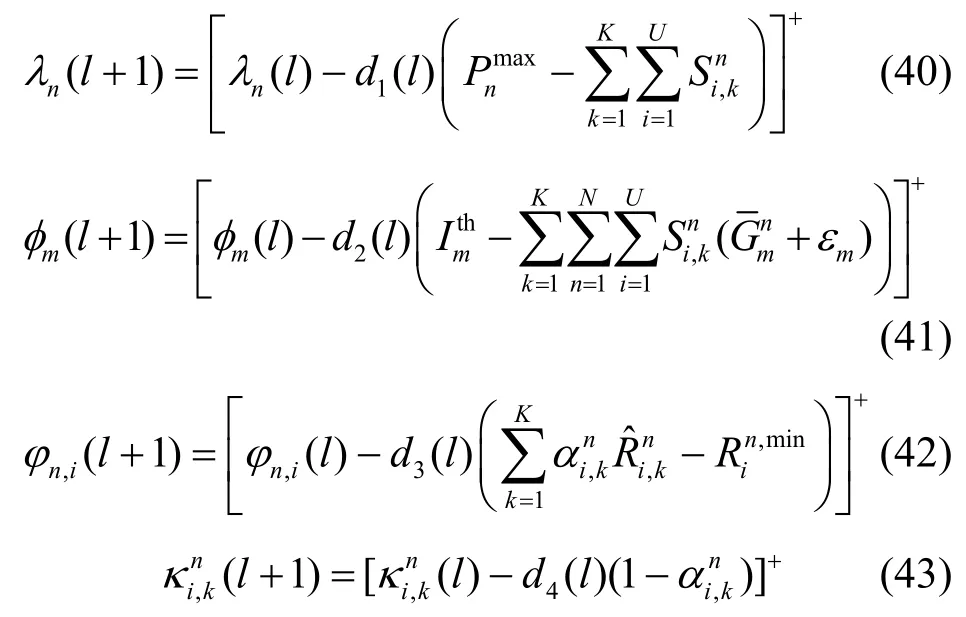
其中，l表示迭代次數，d1、d2、d3和d4表示步長。基于凸優化理論，當?z∈{1,2,3,4}時，本文算法能夠保證收斂到最優值[19]。小蜂窩迭代能效資源分配算法如算法1 所示。

算法1小蜂窩迭代能效資源分配算法

初始化閾值為；輔助變量t；估計誤差上界為；定義最大迭代次數為Xmax；收斂精度為?；初始化外層迭代次數x=0。

初始化拉格朗日乘子及對應步長；定義內層最大迭代次數Lmax；初始化內層迭代次數l=0 ；

4) 根據式(40)～式(43)更新拉格朗日乘子λn(l)，φm(l)，?n,i(l)，

3.4 穩健資源分配算法復雜度分析

假設外層能量效率和內層拉格朗日法的最大迭代次數分別為Xmax和Lmax。對每個資源塊進行最優分配需要O(NU) 次運算。根據式(40)～式(43)，拉格朗日乘子的更新復雜度為O(MNKU)。由于內層迭代次數Lmax是一個關于迭代次數的多項式，需要O(LmaxMN2KU2)次運算。Dinkelbach 法外循環求解的最大計算復雜度是一個超線性時間復雜度形式O(Xmax)[20]。因此，本文算法的多項式時間復雜度為O(XmaxLmaxMN2KU2)。

4 仿真分析

本節通過仿真分析驗證本文算法的有效性。假設系統中存在一個宏蜂窩網絡、2 個宏蜂窩用戶和2 個小蜂窩網絡，每個小蜂窩網絡中含有2 個小蜂窩用戶。宏蜂窩和每個小蜂窩的半徑分別是500 m和20 m，不同小蜂窩之間的最小距離是40 m。信道衰落模型包含瑞利衰落、陰影衰落和路徑損耗，其中路徑損耗指數為3，其他參數如表2 所示。

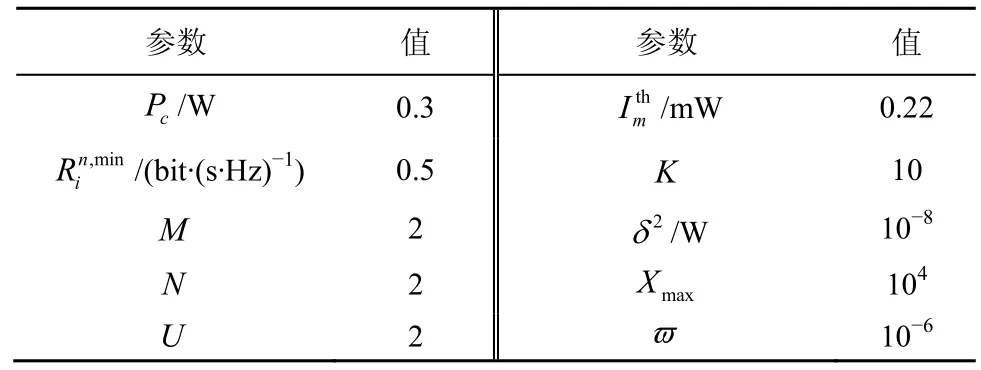
表2 仿真參數

本文算法的收斂性能曲線如圖2 所示。假設每個小蜂窩基站的最大發射功率為1.2 W。從圖2 中可以看出，本文算法具有較好的收斂性。在迭代初期，隨著迭代次數的增加，每個小蜂窩用戶的發射功率總體呈增加趨勢，當迭代大約12 次時，小蜂窩用戶的發射功率達到收斂。收斂后能夠滿足小蜂窩基站的最大發射功率約束，說明本文算法可以很好地保障小蜂窩用戶的通信質量。

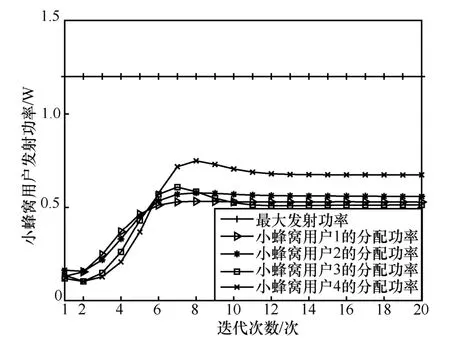
圖2 本文算法的收斂性能

小蜂窩網絡最大發射功率和系統電路功耗對能量效率的影響如圖3 所示。假設其他系統參數相同，可以看出，當電路功耗不變時，隨著最大發射功率閾值的增加，小蜂窩網絡的能量效率增加。因為小蜂窩網絡最大發射功率閾值越大，允許小蜂窩基站分配越多的功率給小蜂窩用戶，傳輸速率越快，因此小蜂窩網絡的能量效率越大。從另一個層面講，考慮相同的發射功率閾值，能量效率會隨著電路功耗的增加而減小。這是因為電路功耗越大，小蜂窩網絡消耗的功率越多，能量效率也就越小。

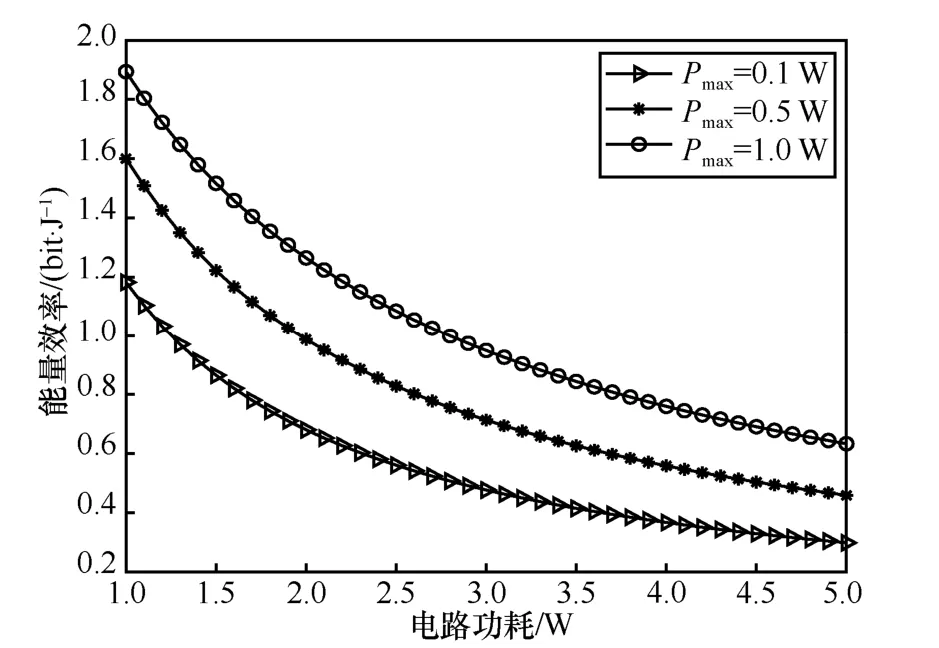
圖3 最大發射功率和系統電路功耗對能量效率的影響

跨層干擾閾值和最小數據速率對小蜂窩網絡能量效率的影響如圖4 所示。可以看出，在相同最小數據速率下，小蜂窩網絡的能量效率隨跨層干擾閾值增大而增大。因為增大跨層干擾閾值會增大發射功率的可行域。另一方面，考慮相同的跨層干擾閾值，能量效率隨著最小數據速率增加而減小，這是因為為了滿足最小速率的要求，小蜂窩基站必須提升發射功率，因此小蜂窩網絡的功率消耗會增大，導致能量效率的降低。

圖4 跨層干擾閾值和最小數據速率對能量效率的影響

干擾功率約束中不確定性對能量效率的影響如圖5 所示。設置不確定參數上界εm分別為0.2、0.4、0.6。可以看出，在相同的跨層干擾閾值下，隨著不確定參數的增大，小蜂窩網絡的能量效率也增大。通過式(8)可知，不確定性增大會使發射功率減小，導致小蜂窩網絡的功率消耗減小，因此能量效率會增大。

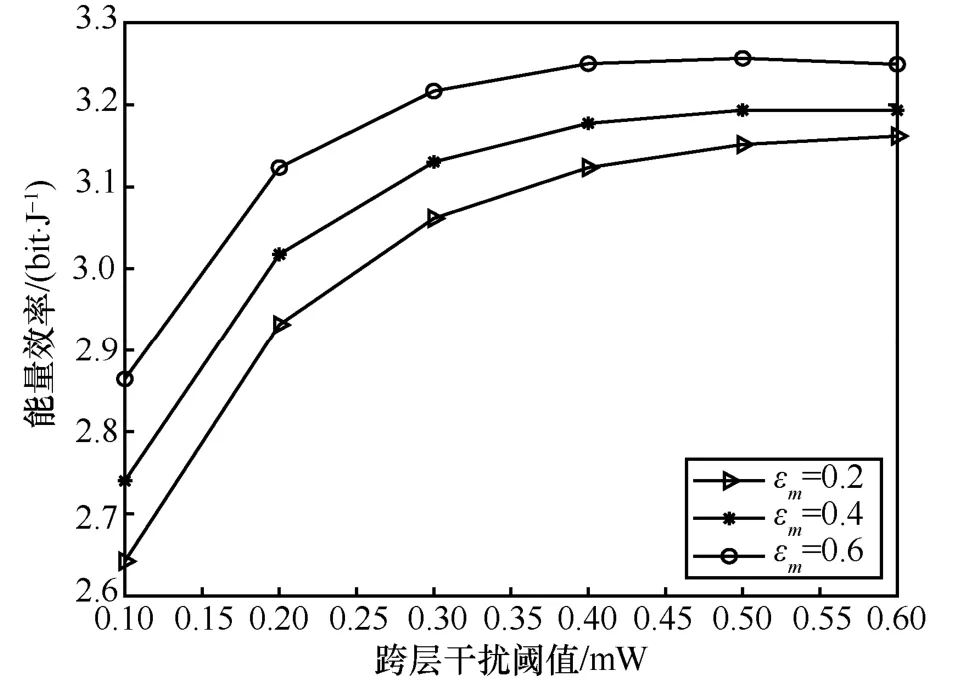
圖5 干擾功率約束中不確定性對能量效率的影響

速率的不確定性對能量效率的影響如圖6 所示。可以看出，考慮相同的跨層干擾閾值和不確定參數，能量效率隨著不確定參數的增大而增大。因為不確定參數的增大會導致信干噪比減小，連續凸近似法中的系數會減小，從而發射功率減小，小蜂窩網絡的功率消耗減小，因此能量效率會增大。另一方面，考慮相同的跨層干擾閾值和不確定參數，隨著增加，能量效率會降低，這是因為越大，信道環境越差，從而導致小蜂窩網絡能量效率越低。

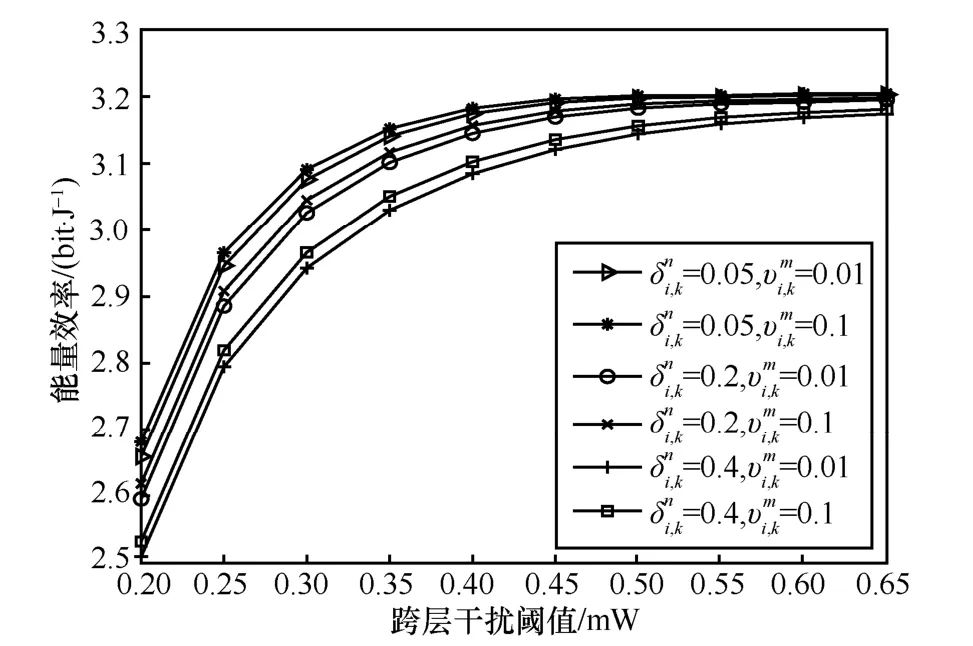
圖6 速率的不確定性對能量效率的影響

不確定性對小蜂窩用戶數據速率的影響如圖7所示。可以看出，隨著信道不確定性Δh的增加，小蜂窩用戶的數據速率會增加；隨著Δg的增加，數據速率會減小。另一方面，當信道不確定性達到一定值后，非穩健算法的數據速率低于最小數據速率，而本文算法能夠很好地控制在最小數據速率以上，這說明本文算法具有良好的穩健性。

圖7 不確定性對小蜂窩用戶數據速率的影響

5 結束語

本文針對基于能效最大的NOMA 異構網絡穩健資源分配問題進行研究。考慮了小蜂窩用戶的QoS 約束、小蜂窩基站最大發射功率約束、宏用戶干擾功率約束及資源塊分配約束，建立了多用戶能效最大的資源分配問題。針對難以求得解析解，利用凸松弛法、Dinkelbach 法和連續凸近似法，將原問題轉化成等價的凸優化問題，并通過拉格朗日對偶法求得解析解。仿真結果表明本文算法具有良好的能效和穩健性。