基于變量依賴關系模型的變量重要性度量方法

田興亞， 牟永敏， 張志華

(北京信息科技大學網絡文化與數字傳播北京市重點實驗室，北京 100101)

軟件系統的運行實質上是程序變量按照程序員指定的邏輯相互影響來執行的。Concas等[1]研究了十余款大型軟件系統，發現了軟件系統中的變量分布符合冪律分布，具有非常明顯的復雜網絡特征。為了提高軟件系統的安全性，就應該找出那些重要變量，因為一旦這些變量出現問題就會給軟件系統帶來巨大的損失，如何識別出重要變量是一個非常有價值的研究課題。

在軟件開發過程中，軟件系統面臨各種各樣需要變更的情況，包括增加模塊、修改模塊和刪除模塊。這些操作通常會涉及對變量的變更，由于變量間存在依賴關系, 使得變量的變更引起其他相關聯的變量發生變更，最終引起軟件故障。因此挖掘出變量的重要性，降低變量變更的代價，對軟件測試和維護具有重要的意義。

在軟件系統中, 變量的重要性有所不同。當某個變量發生變更時, 其對于整個程序的影響程度也不同, 尤其是重要的變量發生變化可能會對整個程序產生影響。在軟件結構中，衡量一個變量是否重要，最重要的是衡量變量與其他變量的交互程度。在程序中使用的變量都直接或間接地相互影響，因此分析變量間的依賴關系對變量的重要性度量具有重要的作用。

目前，由于中外學者的關注點不同，所以針對不同場景提出了各種依賴關系，主要包括實體依賴關系、類依賴關系、函數依賴關系、語句依賴關系和變量依賴關系等。

Stevens等[2]首先提出用依賴關系來衡量一個構件對另一個構件的依賴程度。依賴程度越高，構件的耦合性越高。為了便于理解各種依賴關系, 研究者們提出許多依賴圖的模型來描述各種依賴關系。

黃雅菁等[3]利用軟件系統中類和類之間的依賴關系，提出一種基于賦權類依賴圖的重構定位方法，定位需要重構的類。成小芹等[4-5]將中介中心性和類依賴關系圖相結合度量類重要性，有效地指導了測試資源的分配。

符煒等[6]討論了函數依賴關系，并結合程序切片技術，基于函數依賴圖進行構件抽取。程曉菊等[7]將函數依賴圖精簡為函數切片依賴圖得到與代碼變化相關的函數最小集，極大地約簡了測試用例集，提高了回歸測試的效率。

吳軍華等[8-9]提出基于程序依賴圖進行程序代碼的克隆檢測，又采用依賴邊類型約束計算近似解，有效地提高了計算性能。

Harman等[10]闡述了變量依賴分析問題與切片之間的關系，并實現了變量依賴關系分析的VADA系統。DaimlerChrysler公司目前正在利用它作為測試用例自動生成方法的一部分。論文引入的方法為變量依賴關系分析增加了一個新的維度，即增加了對重要變量的自動跟蹤。

Sadi等[11]提出了一種基于自動生成的依賴圖分析變量依賴關系的方法，依賴圖描述了程序變量之間的關聯關系，其中變量作為圖的頂點，變量之間的依賴關系作為圖的邊。通過自動生成的依賴關系圖可以跟蹤關鍵變量，關鍵變量作為檢測程序順序執行的關鍵，優于現有的程序分析方法。但是該方法只分析了變量間的數據依賴關系，未考慮變量間控制依賴關系以及函數調用引起的變量依賴關系。

潘亞飛等[12]通過分析變量間的依賴關系，生成變量數據拓撲圖。為由變量帶來的軟件變更問題提供了新的解決方法。

傅妤婧等[13]針對時態實體依賴圖提出時態實體依賴關系，并分析時態實體依賴圖的節點中心性、節點重要性、節點依賴度和邊的重要性等4個度量指標。

節點的重要性度量方法有度中心性[14]、介數中心性、接近中心性[15]、特征向量中心性[16]等。

現有的依賴分析方法大多針對類、函數和語句的粒度來建模，文獻[12]雖然分析了變量間的依賴關系，為分析由變量引起的軟件變更提供了新思路。但是卻未深入分析哪些變量是能對程序產生更深度影響的變量，不能輕易發生變更。論文結合以上研究成果, 提出變量依賴關系模型的定義，并提出基于變量依賴關系模型的變量重要性度量(variable node importance measure，VNIM)方法，通過實驗分析，證明了該方法在變量重要性度量方面的優越性。

1 相關定義

定義1變量依賴關系模型(variable dependency model,VDM)：VDM=(V,E)，其中V是VDM模型中所有的變量集合，V={vi|vi∈程序變量}。E是VDM模型中變量之間依賴關系的邊集合，E={eij=(vi,vj)|vi,vj∈V} 。其中，eij的定義為

(1)

定義2依賴關系：由控制條件引起的控制依賴和由訪問變量引起的數據依賴以及由函數調用引起的函數依賴。

定義3數據依賴(data dependency)：設s為程序P的賦值語句，令vi為在s中被賦值的變量，Ref(s)為在s中被使用的變量集合，若存在變量vj∈Ref(s)，則稱變量vi數據依賴于變量vj，記為dd(vi,vj)。數據依賴描述了在賦值語句中左部對右部的依賴關系。

定義4控制依賴(control dependency)：設s1和s2分別為程序P的賦值語句和控制語句，令vi為在s1中被賦值的變量，vj為在s2中控制條件的變量，若s1能否被執行由s2的執行狀態決定。則稱變量vi控制依賴于變量vj，記為cd(vi,vj)。

定義5函數依賴(function dependency)：變量v的取值依賴于函數F返回值，則稱變量v函數依賴于F，記為fd(v,F)。

定義6隱含依賴關系(implicit dependency)：隱含依賴關系是指針變量參與賦值運算(地址賦值運算“&”、指針解引用的賦值運算“*”)引起的變量依賴關系，若變量vi隱含依賴于變量vj，則隱含依賴關系可以表示為id(vi,vj)。指針變量是存儲地址類型數據的變量，對于指向同一塊內存地址的指針變量而言，通過任意指針改變該內存的數值時，指向該內存的所有指針變量的取值都將被改變，因而它們屬于相互依賴的隱含依賴關系。

定義7變量重要性的評判標準：變量是否重要取決于應用場景和用戶給定的標準，現針對由變量引起的軟件變更場景提出變量重要性的評判標準。

標準1一個變量是重要的當且僅當有很多重要的變量依賴于它。

標準2一個變量是重要的當且僅當它接近變量依賴關系模型的中心。

標準1遞歸地定義一個變量是否重要取決于 2個要素：①依賴于該變量的變量數量越多，變量越重要；②依賴于該變量的變量重要性越高，變量越重要。根據標準1的定義可知，如果一個變量被很多其他變量依賴，那么對這個變量的修改可能會影響許多依賴于它的變量;如果一個變量被重要的變量依賴，那么對這個變量的修改可能會影響到重要變量從而對軟件產生較大的影響。

標準2定義變量的重要性取決于變量的中心性，中心性越高的變量被刪除后對變量依賴關系模型的破壞程度就越大，也就說明這些變量越重要。

對于不同類型的代碼語句定義了不同的變量依賴關系如表1所示。

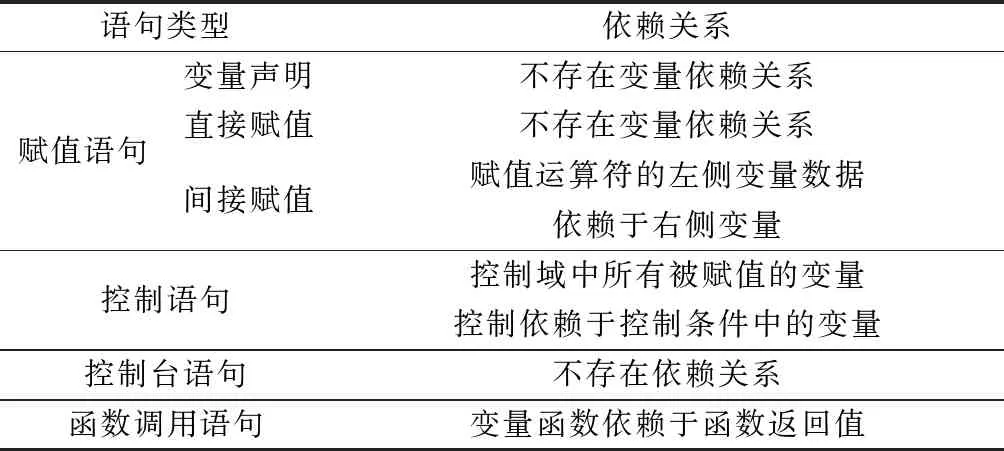
表1 不同類型語句的變量依賴關系

2 變量依賴關系模型的構建

2.1 變量依賴關系分析

2.1.1 數據依賴關系分析

變量的數據依賴體現在代碼中的賦值語句上，在賦值語句的算術表達式中，等號左側的變量數據依賴于等號右側的變量，該語句作用是賦值等操作。如式(2)所示兩行賦值語句：

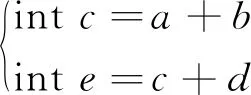
(2)

假設所有的變量有意義，變量c的取值取決于表達式等號的右側變量a和b。變量a和b的任何變化都會引起變量c的變化，這是變量c對變量a和b的直接依賴。變量e的取值同時受到變量c和d的影響，因此變量a和b通過直接影響變量c，從而間接影響變量e。

2.1.2 控制依賴關系分析

在程序代碼中，控制節點體現了程序的邏輯結構，反映了程序執行的走向，包含了變量的控制流和數據流信息。因此，分析控制依賴關系對收集程序的關鍵信息具有重要作用。圖1所示的C程序代碼中6～10行為含有控制依賴關系的代碼段，變量h的取值控制依賴于變量con。當滿足控制語句的判別條件時，函數f的返回值影響變量h，不滿足條件時，變量e影響變量h。

圖1 C程序片段示例Fig.1 C program fragment example

2.1.3 函數依賴關系分析

函數依賴是一種特殊的數據依賴，由于源代碼中的功能塊用函數進行封裝，所以需要做函數層面的變量依賴關系分析，即需要函數返回值的依賴影響關系。例如intq=f1(5)，f1函數定義如圖2所示。

圖2 f1函數Fig.2 f1 function

變量q的取值依賴于函數f1的返回值，即q函數依賴于f1中的變量b。在f1函數中，變量b數據依賴于變量c，同時控制依賴于變量a。變量q的函數依賴關系如圖3所示。

圖3 變量q的函數依賴關系Fig.3 Function dependency of variable q

2.1.4 隱含依賴關系分析

如圖4所示，第 4行定義一個整型指針b,并且b指向了a的地址。第5行定義一個整型的指針c并且c指向了b的地址。假設a、b、c的內存地址分別為0x100、0x200、0x300，則三者之間的訪問形式如圖5所示。

圖4 含指針的C程序Fig.4 C program with pointer

圖5 指針變量的訪問形式Fig.5 Access form of pointer variable

指針b可以通過訪問變量a的地址訪問到變量a的值，屬于直接訪問的形式。指針c可以通過b再訪問a的地址訪問到變量a的值，屬于間接訪問的形式。假如重新對變量a進行賦值，令a=10，則b和c訪問的值也會變為10。因此，指針變量b和c依賴于變量a。令*b=20，通過解引用，可以重新給a賦值為20，同理**c也可以重新給a賦值為20。因此，變量a也依賴于指針變量b和c。由此，可以認為對于指向同一塊內存地址的變量而言，它們屬于相互依賴關系。

算法1描述了變量間依賴關系的提取算法，此算法的主要目標是查找變量并提取變量間的依賴關系。抽象語法樹中含有程序的所有的信息，抽象語法樹可以理解為源代碼的樹形結構，樹中的每個節點信息都和源代碼的信息一一對應。需要對抽象語法樹中的節點進行遍歷和解析，提取變量、函數、賦值信息和控制信息等關鍵信息。根據節點中關鍵字的不同，定義不同的依賴關系。并將相應的變量和依賴關系類型標簽加到結果集中。算法1如下：

算法1 變量間依賴關系的提取算法輸入:預處理后的源程序輸出:變量依賴關系集合定義:令mark為變量依賴關系類型標簽Step1:利用抽象語法樹生成工具得到源代碼樹形結構的數據,源代碼的信息和樹中的節點信息一一對應。Step2:基于抽象語法樹,從 node 的根節點開始遍歷,提取變量、函數、賦值信息和控制信息等關鍵信息。Step3:遍歷關鍵節點,若存在賦值關鍵字“assign”,則令mark=“dd”;若存在循環控制關鍵字“for”、“while”或“if”分支控制字,則令mark=“cd”;若存在函數調用關鍵字“call”,則令mark=“fd”; 若存在指針類型的關鍵字如“array” 或“pointer”,則令mark=“id”Step4:將變量和相應的依賴關系標簽加入到結果集中。Step5:循環上述過程,直到整個對象全部遍歷完成。

在圖1的示例代碼中，變量c數據依賴于a和b，變量e數據依賴于c和d。變量h控制依賴于變量con、函數依賴于f和數據依賴于變量e。對程序變量的依賴關系分析過程如表2所示。

表2 程序變量的依賴關系分析

2.2 變量依賴關系模型構建的方法實現

提取變量間的依賴關系之后，如前文所述，利用變量間的依賴關系生成變量依賴關系模型。變量依賴關系模型的頂點是代碼段的變量,邊由依賴變量指向被依賴變量。

算法2描述了變量依賴關系模型構建的實現過程。以變量依賴關系集合作為輸入，遍歷變量依賴關系集合，得到集合中每個變量及其依賴關系；提取變量并繪制變量節點，如果變量i與變量j之間存在依賴關系，提變量依賴關系類型標簽，繪制一條從變量i到變量j的邊，并把標簽的取值賦值給邊；循環上述過程直至遍歷完成，最終得到變量依賴關系模型。算法2如下：

算法2 變量依賴關系模型構建算法輸入:變量依賴關系集合r_array輸出:變量依賴關系模型1. Begin each element of r_array2. Draw parent3. Until all elements of r_array traversed4. If parent has child5. For each child of child_arr6. Draw child7. Draw edge from parent to child8. set edge_value=mark9. End loop10. elif parent in child of new_parent11. child=parent, parent=new_parent12. Draw edge from parent to child13. set edge_value=mark14. else draw parent15. End loop16. End

將算法2應用于圖1的示例程序，最終得到變量依賴關系模型。圖6繪制了程序從第1～10行變量依賴關系模型的逐步構建過程。

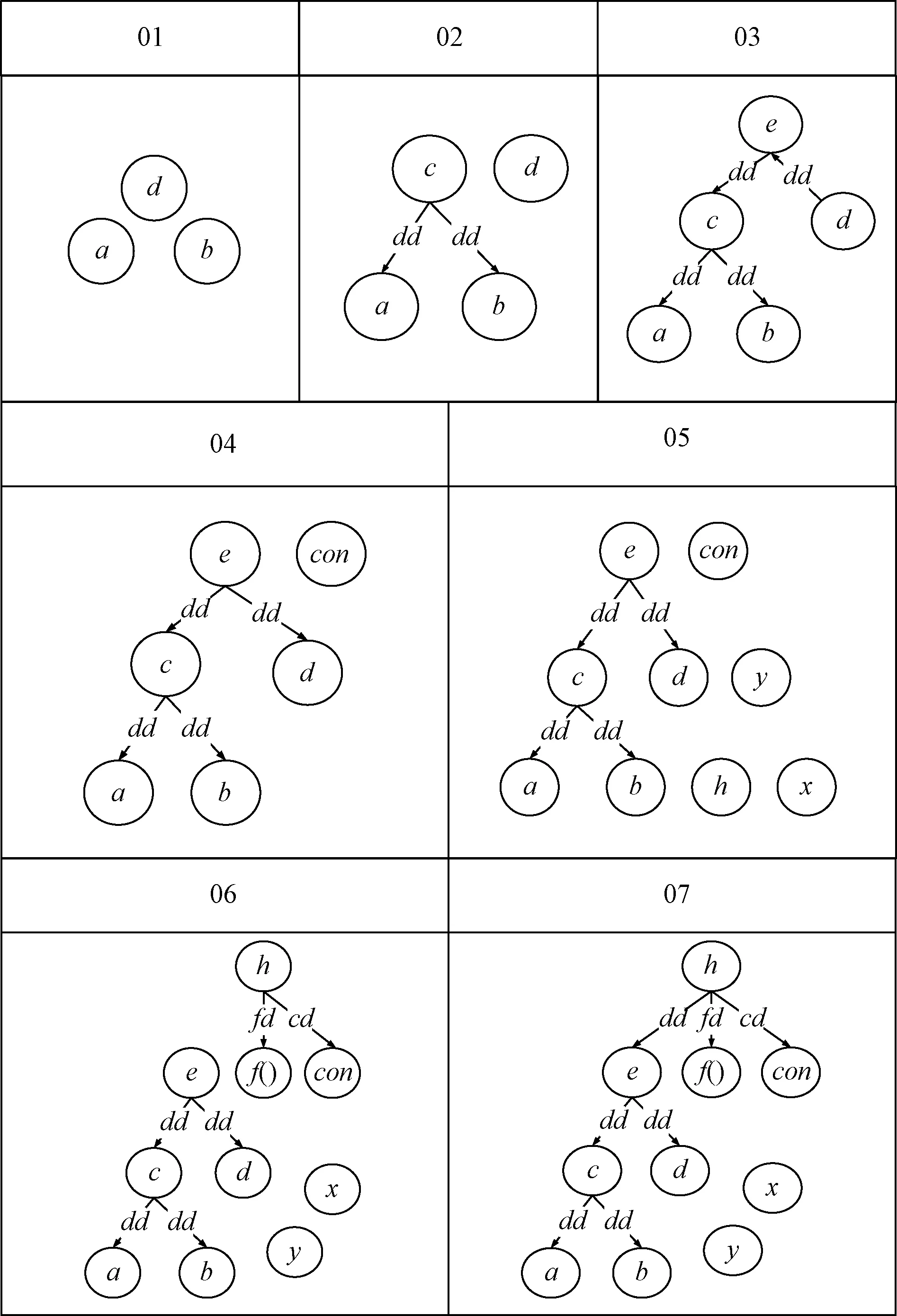
圖6 變量依賴關系模型自動生成過程Fig.6 Variable dependency model automatic generation process

變量依賴關系模型是程序中變量信息傳播的直接映射，反映了程序中變量的相關依賴信息如控制依賴信息和函數依賴信息等。

變量依賴關系模型的功能如下。

(1)自動跟蹤程序中的變量和方法，明確變量和函數調用在整個程序中的分布情況。

(2)跟蹤變量在整個程序中的使用情況及其依賴關系，依賴關系包含了變量的數據依賴關系、控制依賴關系、函數依賴關系和指針引起的隱含依賴關系。

(3)可以直觀地展示各變量間依賴關系類型及其傳播方向。

(4)通過變量依賴關系模型并結合變量的出度和入度可以分析變量在程序中的重要性。

(5)當出現變量問題引起的軟件錯誤時，通過變量依賴關系模型可以快速定位到最可能出錯的根源變量，可以有效地指導軟件測試活動。

3 基于VDM的變量重要性度量方法

3.1 相關概念

3.1.1 節點中心性

在網絡圖中，節點中心性(node centrality)可以表示節點在圖中與其他節點相關聯的程度。中心性越高，與其他節點的關聯程度就越高，該節點能夠影響到的其他節點就越多。

節點中心性定義如下：

(3)

式(3)中：in(pi)代表在網絡圖中節點pi的入度；out(pi)表示節點pi的出度；N表示節點總數。

在網絡圖中，假設節點pi的度為deg(pi)，則節點pi的中心性也可以表示為

(4)

中心性只考慮了節點在網絡中的位置，并沒有考慮依賴于該節點的節點重要性貢獻，也并未考慮節點本身的重要性信息，考慮較為片面。

3.1.2 節點重要性

傅妤婧[13]提出的節點重要性(node importance)與中心性相比，更多地關注了節點的入度。即節點的入度數越大，依賴于該節點的其他節點個數越多，當該節點發生改變時，會有更多的節點直接受到其影響。

定義節點的重要性為直接依賴于該節點的所有節點中心性之和。則節點pi的重要性為

(5)

式(5)中：C(pj)表示依賴于節點pi的節點pj的中心性。

式(5)的節點重要性計算方法除了考慮節點鏈入數量的因素，還結合了鄰接節點的中心性影響因素。但該方法有一個很大的缺陷，假如一個節點沒有任何鏈入，則該節點的重要性為0，這顯然是不合理的。該方法一定程度上刻畫了節點的重要性，但同時也忽略了很多因素，僅僅考慮鄰接節點的數量和中心性情況，以此來衡量節點的重要性，有很大的局限性。

3.1.3 PageRank方法

PageRank方法是Google著名的網頁重要性排名算法，該算法是特征向量中心性的一個變種。PageRank值越大表示網頁重要性越高。

假設存在節點pi，則其PageRank值計算方式如下：

(6)

式(6)中：M(pi)代表鏈入節點pi的節點集合；Lo(pj)表示節點pj的鏈出數；N代表所有的節點總數；α是阻尼系數，針對網頁排序其取值一般為0.85。

PageRank方法認為節點是否重要取決于兩點：依賴于該節點的數目和這些鄰接節點的重要性。但是卻忽略了節點的中心性因素，根據節點在網絡中所屬的位置不同，其對信息傳播的作用也是不相同的。

基于上述思想，并結合定義6提出的變量的重要性評判標準，引入了“樞紐性”來衡量變量在變量間信息傳播的作用即中心性影響，并結合鄰接變量的重要性貢獻提出了一種新的基于變量依賴關系模型的變量重要性度量(variable node importance measure,VNIM)方法。

3.2 VNIM方法

重要變量指的是能對程序產生更深度影響的變量，其影響包括對程序信息的傳播以及對全局變量的鏈接作用。PageRank 方法只考慮了鄰接節點的重要性貢獻，卻未考慮節點本身的樞紐性，考慮較為片面。樞紐性是指節點所在位置，反映了節點的中心性影響。針對PageRank存在的局限性問題，提出VNIM方法，方法不僅考慮了鄰接節點的重要性貢獻，還結合了節點的樞紐性作用。

假設存在變量vi,則其VNIM的計算方式為

(7)

式(7)中：DP(vi)表示依賴于vi的變量集合；IC(vj)表示變量vj對變量vi的重要性貢獻度；VNIM0(vi)表示變量vi的初始重要性；H(vi)表示變量vi的樞紐度(hub Degree)。

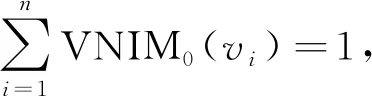
(8)

式(8)中：N代表所有的變量總數。

重要性貢獻度(importance contribution)： 若存在一條變量依賴關系vj→vi，變量vj對變量vi的重要性貢獻度為變量vj自身的重要性與其出度的比值，即:

IC(vj)=VNIM(vj)/o(vj)

(9)

式(9)中：o(vj)表示變量vj的出度。

樞紐度H(vi)的定義如下：

H(vi)=C(vi)

(10)

C(vi)的定義曾在式(5)提到，表示變量的中心性。變量的樞紐度等于其中心性，反映了變量在變量間信息傳播的作用。

為了消除程序規模對變量重要性的影響，需要對變量的重要度做歸一化處理如下：

(11)

變量的VNIM是由所有依賴于該變量的其他變量重要性經過遞歸算法得到的。除了考慮鏈入變量的數量及鄰接變量的重要性貢獻因素，還結合了變量的樞紐性影響，綜合兩者因素可以獲得更好的度量結果。

如果一個變量被很多變量依賴，或被少數幾個重要的變量依賴，則變量的重要性較高。因此，有較少鏈入數的變量可能比有較多鏈入數的變量重要性更高。同時根據變量樞紐性作用的不同，變量的重要性也不相同。

VNIM方法具有如下性質。

(1)傳遞性：由于VNIM的計算考慮了鄰接變量的重要性貢獻因素，因而VNIM方法具有傳遞性。

假設變量b、c和d依賴于變量a，那么變量a的VNIM與其樞紐度的比值為變量b、c和d對變量a的重要性貢獻度與變量a初始重要性之和。

則變量a的VNIM與其樞紐度的比值為

(12)

(2)傳遞的均勻性：變量的VNIM值均勻地向后傳遞。

假設變量a和c依賴于變量b，變量a，e和f三個變量依賴變量d。變量a、b、c、d、e和f之間的依賴關系如圖7所示。

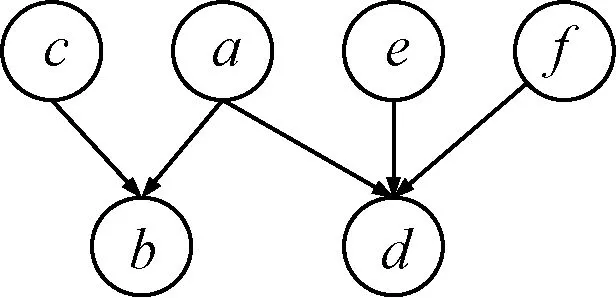
圖7 變量依賴關系示例圖Fig.7 Sample diagram of variable dependencies

則變量a、e和f對變量d的重要性貢獻度分別為

(13)

鄰接變量對變量的重要性貢獻度與鄰接變量的出度成正比，變量a既依賴于變量b又依賴于變量d，因而變量a對變量d的重要性貢獻度為變量a自身的重要性的1/2。

4 實驗分析

通過一個VDM示例圖將VNIM方法與傅妤婧[13]提出的節點重要性度量方法和PageRank方法進行對比，展示VNIM方法在變量重要性度量方面的準確性。用例圖如圖8所示。

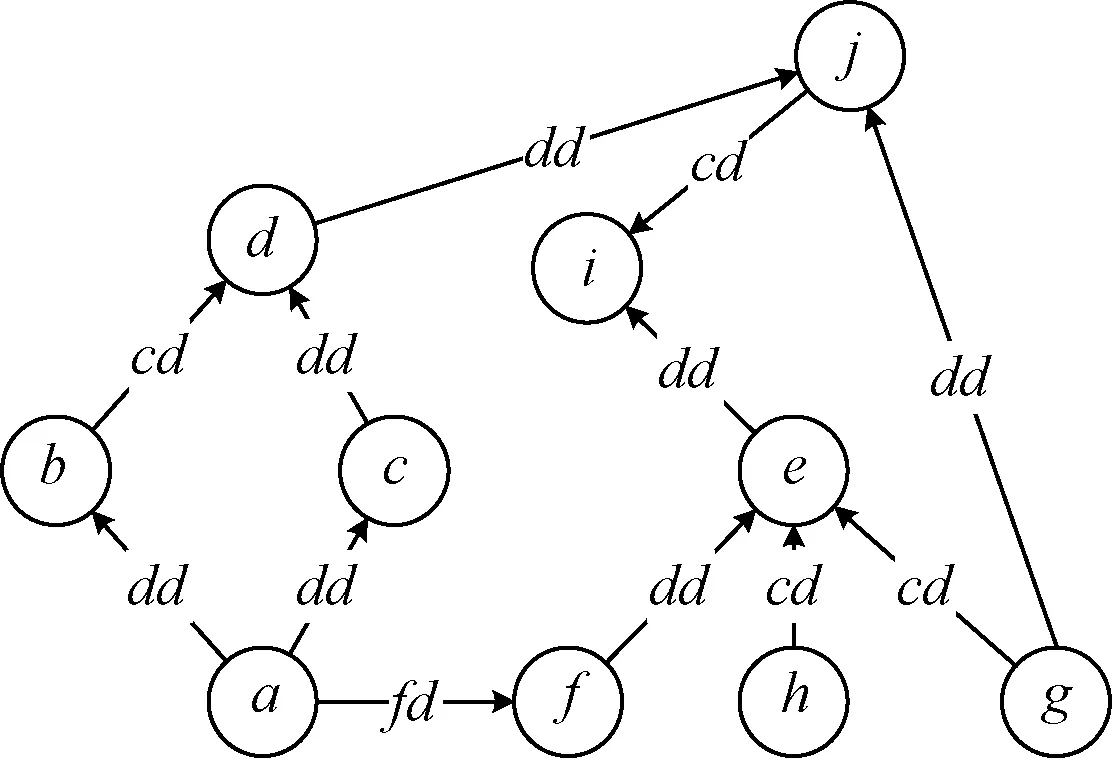
圖8 VDM示例圖Fig.8 VDM example diagram

利用本文描述的方法，可以計算出VDM示例圖中各個變量的中心性值、NI值、PageRank(PR)值和VNIM值，計算結果如表3所示。

表3 各種指標計算結果

通過計算結果的呈現，可以發現這幾種方法對變量重要性的排名結果有所不同。

通過表3可以發現，通過傅妤婧[13]提出的節點重要性度量方法計算得出變量a、g和h的重要性為0，這顯然不合理，因為變量a、g和h雖然不被任何其他變量所依賴，但是它們在變量的信息傳播中起到了重要的作用。同時，計算結果中出現了很多變量重要性相同的現象，如變量b、c、f和j的重要性完全相同，這是由于NI值的計算方法只關注了其鄰接變量的中心性指標，未考慮變量間信息的傳播，也未考慮變量本身的重要性信息等，考慮較為片面。而在變量依賴關系模型中，可能會出現大量變量的中心性一致的情況，在程序規模足夠大的情況下，可能會導致變量的重要性難以有效區分。

表4為各個變量重要性的排名結果，括號內的數字表示排名的并列情況。由于變量i幾乎被所有變量直接或間接地依賴，因而能對程序產生更深度的影響。所以在PageRank方法中，變量i排名第一。傅妤婧[13]提出的節點重要性度量方法只考慮了鄰接變量的中心性因素，同樣得出變量i最為重要。 而VNIM方法結合鄰接變量的重要性貢獻以及變量在信息傳播的作用，也把變量i排在了第一位。

表4 變量重要性排名結果

雖然三種方法都把變量i排在了第一位，但是其考慮的因素卻大大不同，尤其是傅妤婧[13]提出的節點重要性度量方法在變量重要性度量方面有明顯缺陷。對比VNIM方法和PageRank方法，排名結果中出現較大差異的為變量a、g和h的重要性排名結果，在PageRank方法中三者重要性相同，而在VNIM方法中的排名為a>g>h。仔細觀察圖6可以發現，變量a、g和h的入度都為0，出度分別為3、2和1。入度為0表明即沒有任何變量依賴于這些變量，由于PageRank重點關注的是鄰接變量的重要性貢獻和數量，并沒有考慮變量的樞紐性影響因素，所以得出三個變量的重要性相等的結論。而VNIM方法既考慮了鄰接變量的數量以及重要性貢獻，又綜合了變量的樞紐性影響因素，因而與前者的排名結果不同。

顯然，變量a、g和h的重要性是不同的，雖然不被任何變量依賴，但是變量起到了信息傳播的作用，根據變量的中心性不同，其傳播作用的大小也不相同。變量a的度更大，起到的樞紐性作用更大，能對程序產生更深度的影響，因而變量a相比變量g和h的重要性要更大一些。同理，變量e的重要性大于變量j，變量a的重要性大于變量b、c和f。

從表4可以看出，PageRank方法和NI方法的排名結果出現了很多變量重要性一致的情況，尤其是NI方法的排名結果最為明顯，變量b、c、f和j重要性完全一致。VNIM方法結合了鄰接變量的重要性貢獻和變量的樞紐性作用，綜合衡量變量在程序中的重要性，彌補了其他兩個方法的不足，其重要性排序結果更為準確合理。

上述的分析結果說明VNIM方法對比傅妤婧[13]提出的節點重要性度量方法和PageRank方法在評價變量重要性度量方面更加準確有效，變量重要性排序結果更具有實際意義。

在變量依賴關系模型中，衡量變量是否對程序產生了更深度的影響，不僅要考慮依賴于該變量的數量和重要性貢獻，還要結合變量在信息傳播中的作用。VNIM方法充分利用了變量間的依賴信息，對變量的重要性度量結果更加準確。

5 結論

變量重要性度量是軟件測試領域的重要研究點，尤其是在變更影響分析和測試用例的生成、排序和優化方面具有很重要的作用。提出利用變量之間的依賴關系構建變量依賴關系模型。自動生成的變量依賴關系模型描述了變量之間的所有依賴關系，包括數據依賴關系、控制依賴關系、函數依賴關系以及指針引起的隱含依賴關系，并將圖論和程序變量重要性度量相結合，基于變量依賴關系模型進行變量的重要性度量。根據變量在變量間信息傳播的作用，提出變量“樞紐性”的概念，并通過實驗證明了該方法在分析變量重要性度量方面更加有效。

在軟件生命周期中，許多軟件錯誤是由變量問題引起的，通過變量依賴關系模型可以快速定位到最可能出錯的根源變量。基于變量依賴關系模型變量重要性度量方法，可以更好地評價軟件內部變量的重要性，對變更影響分析和測試用例生成提供了新思路，有利于指導軟件測試和提高軟件的測試效率。