幾類圖運算對受控著色數的影響

周洋洋， 許 進

(北京大學 信息科學技術學院， 北京 100871)

若無特殊聲明，本文所涉及的圖皆指有限、簡單和無向圖.對于給定圖G，分別用V(G)和E(G)表示G的頂點集和邊集，G中所含頂點數(|V(G)|)和邊數(|E(G)|)分別稱為G的階和規模.對任意v∈V(G)，v的開鄰域，記作N(v)，表示G中與頂點v相鄰的所有頂點構成的集合，即N(v)={u|uv∈E(G)}.v的閉鄰域N[v]=N(v)∪{v}. 頂點v的度數，記作d(v)，是指N(v)中元素的個數.用δ(G)和Δ(G)分別表示G的最小度和最大度，并分別簡記為δ和Δ. 設v∈V(G)，S?V(G)，如果v與S中的每個頂點都相鄰，則稱v控制S，也稱S被v控制.令S是G的一個頂點子集，如果S中任意兩個頂點在G中均不相鄰，則稱S為G的一個獨立集.若V′?V，E′?E，且E′中每條邊的兩個端點均在V′中，則稱圖H=(V′,E′)是圖G的一個子圖.設H是G的一個子圖，如果V(H)=V(G)，則稱H是G的生成子圖.如果對于子圖H中任意兩個頂點u和v、u、v在G中相鄰當且僅當它們在H中相鄰，則稱H為G的一個由V′導出的子圖，記為G[V′].用Pn=v1v2…vn-1vn表示n個頂點，長度為n-1的路，并用Cn=v1v2…vn-1vnv1表示n個頂點，長度為n的圈，常將長度為n的圈稱為n-圈.文中未說明的概念及記號，可參見文獻[1].

圖G=(V,E)的一個正常k-頂點著色，是指從頂點集V到顏色集{1,2,…,k}的一個映射f，使得G中任意兩個相鄰的頂點都著不同顏色.事實上，圖的k-頂點著色問題等價于將頂點集V(G)劃分為k個獨立集{V1,V2,…,Vk}，其中Vi={x∈V|f(x)=i}，i=1,2,…,k. 筆者將著相同顏色的頂點的集合稱為一個色組.圖G的色數，記作(G)，是G的一個正常著色所需顏色數的最小值.一個(G)-著色是G的具有最小基數的頂點著色.

圖G的一個控制集是指一個頂點子集S，使得G中每個頂點要么在S中，要么與S中的頂點相鄰.圖G的控制數，記作γ(G)，是指G的一個控制集的最小基數.

圖的著色理論和控制理論是圖論中兩個非常活躍的重要領域，都有著廣泛豐富的研究成果，分別詳見文獻[2-9].此外，許多學者從多個方面討論了這兩個領域之間的聯系，并提出了一些新的概念.

2004年，Chellali等[10]展示了圖的色數與一些控制參數之間的關系.Cockayne等（1）Cockayne E,Hedetniemi S,Hedetniemi S M, et al. Dominator partitions of graphs, Unpublished manuscript, 1979.在1979年引入并介紹了圖的控制劃分的概念，在此推動下，2006年，Gera等[11]提出了控制著色的概念.

圖的控制著色是一個正常頂點著色，使得每個頂點都控制至少一個色組(可能是頂點自身所構成的色組).圖的控制著色數，記作d(G)，是指圖G的一個控制著色中色組的最小值.

在控制著色的基礎上，Kazemi[12]在2015年提出了全控制著色的概念，全控制著色是指一個正常頂點著色，使得每個頂點都與某個色組中的所有頂點相鄰.關于控制著色和全控制著色的更多結論，參見文獻[13-21].

2015年，Merouane等[22]提出了受控著色的概念.圖的受控著色是一個正常頂點著色，使得每個色組都被至少一個頂點控制.圖的受控著色數，記作dom(G)，是指圖G的一個受控著色所需顏色數的最小值.

基于控制著色和受控著色的研究，筆者在文獻[23]中提出了統治著色的概念，并研究得到了一些基本性質和結論.

圖的統治著色，是指一個正常頂點著色，使得每個頂點都控制至少一個色組(可能是頂點自身所構成的色組)，且每個色組都被至少一個頂點控制.圖的統治著色數，記作dd(G)，是指圖G的一個統治著色所需顏色數的最小值.

基于上述概念，學者們自然地關注了另一個有趣的問題：當對圖G實施某些運算時，這些參數會發生什么變化？針對這個問題，Ghanbari等[24]在2016年研究了某些運算對全控制著色數的影響.2018年，Alikhani等[25]討論了一個圖的k-細分圖的全控制著色數.2019年，Alikhani等[26]在研究幾類特殊圖的受控著色數的同時，還討論了它們的受控穩定臨界數，即使得受控著色數dom(G)改變所需刪除的頂點(邊)數的最小值.同年，筆者在文獻[27]中研究了一些圖運算對統治著色數的影響.

1 刪除頂點和邊

頂點和邊的移除是圖運算中最基本的運算，本節討論刪除頂點和刪除邊運算對圖的受控著色數dom(G)的影響.

設v是G中任意頂點，e是G中任意一條邊.G-v是通過在圖G中刪除頂點v以及所有與v相關聯的邊所得到的圖.G-e是通過在G中刪除邊e所得到的圖.

定理1 設G是一個連通圖，v∈V(G)且v不是割點，則

dom(G)-1≤dom(G-v)≤dom(G)+d(v)-1.

證明先證明左邊不等式.給定G-v的任意受控著色，考慮G的受控著色如下：在G-v中添加頂點v和所有相應的邊，給頂點v著一種新的顏色i，其他頂點著色不變.頂點v所在的色組可被v的任意一個鄰點控制，而其他色組仍由原來的頂點控制，這樣得到了圖G的一個受控著色.于是，dom(G)≤dom(G-v)+1.

下面證明右邊部分.對于圖G的任一受控著色，假設頂點v著顏色i，則有下面兩種情況：

情況(1):存在其他頂點著顏色i. 如果存在色組僅被頂點v控制，那么給此色組中的每個頂點一種新的顏色.顯然，至多有d(v)個這樣的頂點.因為v不是割點，每一個新著色的頂點作為一個色組必然被其他鄰點(除v外)控制，而其他色組仍由原來的頂點控制.于是得到了G-v的一個受控著色，且dom(G-v)≤dom(G)+d(v)-1. 如果不存在上述性質的色組，則由圖G原來的著色即可得到G-v的一個受控著色，且dom(G-v)≤dom(G).

情況(2):不存在其他頂點著顏色i. 按照情況(1)的分析，如果存在色組僅被頂點v控制，則dom(G-v)≤dom(G)+d(v)-2. 否則，dom(G-v)≤dom(G)-1.

定理得證.

定理2 設G是一個連通圖，e∈E(G)且e不是割邊，則

證明設e=uv∈E(G). 首先，證明左邊不等式.考慮G-e的一個受控著色，若在G-e中添加邊e，則存在兩種情況：

情況(1):頂點u和v在G-e的受控著色中著相同顏色.對u和v中之一著新的顏色i，其他頂點著色保持不變，這樣就得到了G的一個受控著色，且滿足dom(G)≤dom(G-e)+1.

情況(2):頂點u和v在G-e的受控著色中著不同顏色.那么，G-e的受控著色也是G的受控著色，于是dom(G)≤dom(G-e).

下面證明右邊不等式.考慮G的一個受控著色，假設u∈Vi，v∈Vj，即頂點u著顏色i，頂點v著顏色j. 于是，存在下面三種情況：

情況(1):頂點u不控制色組Vj，且頂點v不控制色組Vi. 在這種情況下，G的受控著色也是G-e的一個受控著色.從而，dom(G-e)≤dom(G).

情況(2):頂點u控制色組Vj，而頂點v不控制色組Vi. 根據定義，u與Vj中每個頂點都相鄰，而Vi必由其他頂點控制.在圖G-e中，給頂點v一種新的顏色k. 由于e不是割邊，G-e是連通圖且頂點v有其他鄰點.那么，v自身構成的色組必被其他鄰點控制，色組Vj{v}被頂點u控制，其他保持不變，這樣得到了G-e的一個受控著色，且dom(G-e)≤dom(G)+1.

情況(3):頂點u控制色組Vj，且頂點v控制色組Vi. 在這種情況下，給頂點u和v分別著新的顏色k和l. 由于e不是割邊，則G-e是連通圖.在新得到的著色中，頂點u和v各自所在的色組都會由它們其他的鄰點所控制.又因其他頂點著色不變，這個新得到的著色即是G-e的一個受控著色，且dom(G-e)≤dom(G)+2.

定理得證.

2 收縮頂點和邊

設圖G=(V,E)，S?V是一個頂點子集，在G中收縮S，記作G°S，是通過將S中的所有頂點替換為一個新的頂點，并將原來與S中頂點相關聯的邊均與這個新的頂點關聯所得到的圖.特別地，當S={u,v}時，有下面兩種情況：

(1) 頂點u和v相鄰，即e=uv∈E(G). 在圖G中收縮邊e=uv，記作G°e，是通過刪除邊e，并將頂點u和v替換為一個新的頂點，使得原來與u或v相鄰的頂點均與這個新的頂點相鄰而得到的圖.收縮邊運算，簡稱為縮邊運算，如圖1所示，其中頂點周圍的黑色省略號標記表示可能存在邊與該頂點關聯.

圖1 縮邊運算Fig.1 The edge contraction operation

(2)頂點u和v不相鄰.將此時的收縮運算記作G° {u,v}，簡稱為縮點運算，如圖2所示.

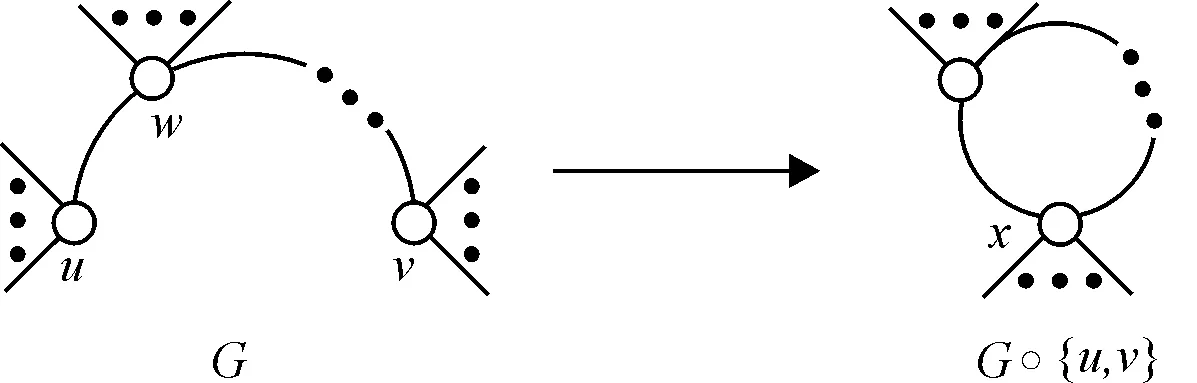
圖2 縮點運算Fig.2 The vertex contraction operation

定理3 設G是一個連通圖，e∈E(G)，則

證明設e=uv∈E(G). 首先，證明左邊不等式.考慮G°e的一個dom(G°e)-受控著色.通過在G°e中添加刪除的頂點以及所有相應的邊，得到圖G. 將e的端點的原來的著色刪除，并對頂點u和v分別著新的顏色k和l，其他頂點著色不變.易驗證，這樣得到的是G的一個受控著色，且dom(G)≤dom(G°e)+2.

再證明右邊不等式.考慮G的一個dom(G)-受控著色f，其中f(u)=i，f(v)=j. 令x是替換u和v的新頂點.下面構造G°e的受控著色.給頂點x著新的顏色k，其他頂點著色不變.頂點x自身構成的色組可由其任意鄰點控制，于是得到了G°e的一個受控著色，且dom(G°e)≤dom(G)+1.

定理得證.

定理4 設G是一個連通圖，u和v為G中任意兩個不相鄰的頂點，則

證明設u，v為G中任意兩個不相鄰的頂點.首先,證明左邊不等式.考慮G° {u,v}的一個dom(G° {u,v})-受控著色.在G° {u,v}中添加刪除的頂點以及相應的邊，得到圖G. 將u和v原來的顏色刪除，并分別給它們著新的顏色k和l，其他頂點著色不變.易驗證，這是G的一個受控著色，且dom(G)≤dom(G° {u,v})+2.

接著，證明右邊不等式.考慮G的一個dom(G)-受控著色f，基于f來構造G° {u,v}的受控著色.令x是替換u和v的新頂點.給x著新的顏色k，其他頂點顏色保持不變.易驗證，這樣得到的是圖G° {u,v}的一個受控著色，且dom(G° {u,v})≤dom(G)+1.

定理得證.

3 邊細分

設G是一個連通圖，k是一個正整數.G的k-細分圖，記作Sk(G)，是通過將G中的每條邊替換成長度為k的路而得到的圖.對于每條邊e=vivj∈E(G)，用Pvivj表示替換vivj的k-路，并稱Pvivj為超邊，Pvivj的任意新頂點都是內部頂點.注意到，如果k=1，則S1(G)=G.

邊的細分是一種典型的圖運算.本節研究一個圖G的k-細分圖的受控著色數，以及dom(G)和dom(Sk(G))之間的關系.

定理5 設G是一個含m條邊的連通圖，k≥2是正整數，則

(m-1)dom(Pk)+dom(Pk+1).

證明首先,證明左邊不等式.設e=uv為G中任意一條邊，Puv=ux1x2…xk-1v是Sk(G)中替換uv的路，如圖3所示.令f是Sk(G)的一個dom(Sk(G))-受控著色，考慮f在導出子圖Puv上的限制，記為f′. 由于f是受控著色，端點u(v)要么自身構成色組，要么和其他頂點同在一個色組，都存在鄰點控制其所在色組，又因Puv內部頂點的著色不變，那么f′的每個色組也必有頂點控制.因此，f′是Puv的一個受控著色，且dom(Pk+1)≤|f′|≤|f|=dom(Sk(G)).

圖3 邊細分運算Fig.3 The edge subdivision operation

下面證明右邊不等式.設G是一個含m條邊的連通圖.對任意u∈V(G)，令N(u)={v1,v2,…,vp}，邊uvi分別由超邊Puvi替換，i=1,2,…,p.類似一般Pk+1的受控著色，可用dom(Pk+1)種顏色給超邊Puv1的頂點著色.對Puvi(i=1,2,…,p)的頂點著色，使得頂點u的著色唯一(即u在Puvi(i=2,…,p)中的著色均與Puv1中一致)，并且滿足

f(Puvi)∩f(Puvj){f(u)}=?，

其中,i,j=1,2,…,p，i≠j，f(Puvi)表示Puvi中頂點的顏色的集合.這樣，用至多(p-1)dom(Pk)+dom(Pk+1)種顏色得到了Puvi(i=1,2,…,p)的一個受控著色.接著，考慮與vi(i=1,2,…,p)相關聯的邊所對應的未著色的超邊.繼續重復上述過程，直到Sk(G)的所有頂點均被著色.注意到，某些位于圈上的頂點會被重復著色，但這不會影響最后結果.容易驗證，最后得到的著色是Sk(G)的一個受控著色，且使用了至多(m-1)dom(Pk)+dom(Pk+1)種顏色.因此，右邊不等式成立.

定理得證.

4 擴圈運算

本節討論擴圈運算，以及受控著色數在擴圈運算下的變化.

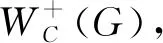
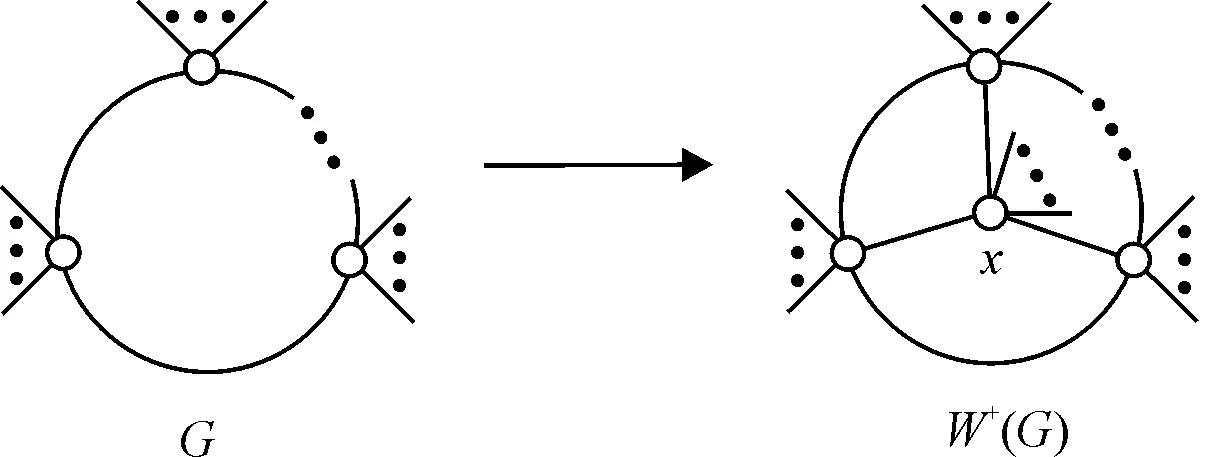
圖4 擴圈運算Fig.4 The cycle extending operation

定理6 設G是一個連通圖，C是G中任意長度為l(≥3)的圈，則

證明首先,證明右邊不等式.對于G的任意一個dom(G)-受控著色，給中心頂點x著一種新的顏色，而其他頂點顏色不變，這樣就得到了W+(G)的一個受控著色.因此，dom(W+(G))≤dom(G)+1.

接著，證明左邊不等式.設f是W+(G)的一個dom(W+(G))-受控著色，下面基于f構造G的一個受控著色，在W+(G)中刪除頂點x及與它相關聯的邊，得到圖G. 需要考慮那些僅被頂點x控制的色組，顯然，這些色組中的元素只可能是圈C上的頂點，因此，只需添加至多l種新的顏色給這些頂點重新著色，就可得到G的一個受控著色.于是，dom(G)≤dom(W+(G))+l.

定理得證.

5 結論與展望