自重作用下吹填土地基的大變形固結分析
邱長林,于博文,閆澍旺,紀玉誠
(天津大學 建筑工程學院,天津 300072)
引 言
天津等沿海城市的人工吹填造地,其主要材料為吹填泥漿等超軟土。由于吹填泥漿含水率高、強度低,需要對吹填地基預處理后再通過真空預壓等方式加固。預處理的一般做法是讓吹填地基在自然風干的條件下自重固結。本課題組通過試驗發現,在吹填土自重固結過程中,自然風干的方法由于在表層形成一密實的硬殼層而阻礙了下部土體的固結,而如果在表層保持一定厚度的覆水將不會形成硬殼層,從而將有可能使整個吹填土地基含水量降低更快。為了評價這種預處理方法的效果并為設計提供依據,迫切需要建立吹填土地基在自重作用下的固結理論。
由于吹填土孔隙比大、壓縮性高,吹填土地基在自重作用下固結變形非常大,同時泥面不斷下降也有效減小了吹填地基中超孔隙水的滲透路徑,所以吹填土地基的變形是一個大變形固結問題,需要采用大變形固結理論。目前的大變形固結理論一般可以劃分為兩種[1],即 Gibson等[2-4]發展的一維大變形固結理論和Carter引進的、建立在非線性連續介質力學理論基礎之上的大變形固結理論[5-11]。其中,非線性連續介質力學大變形固結理論雖然理論上比較嚴謹、擴展性強,但是該理論的固結方程形式復雜,工程應用上受到一定的限制,而 Gibson提出的一維大變形固結理論形式簡單、物理意義明確,且經過長期深入的研究,已形成了較為完整的理論體系。但是該理論以孔隙比e為場變量,無法與傳統 Terzaghi固結理論及 Biot固結理論進行銜接,不便于在這幾種理論之間進行比較,且該理論一般采用常規固結壓力作用下的固結特性,這和吹填土體在自重固結過程中應力較小的特性不符合。
目前對沖填土自重固結問題進行的研究非常少[12],其設計也主要采用小變形理論的Terzaghi固結理論。為此,本文通過室內試驗研究吹填土在小固結壓力作用下的壓縮特性,在Gibson理論的基礎上,建立以超孔隙水壓力為場變量的大變形固結方程,并通過模型試驗對計算結果進行驗證,以期能為吹填土地基的設計及尋求加快其自重固結的途徑提供理論依據。
1 吹填土壓縮特性
1.1 吹填土小荷載作用下的壓縮試驗
為了研究吹填土在小固結壓力作用下的固結特性,需對常規固結儀進行改制,使其固結壓力通過在改制的加壓上蓋上直接添加砝碼的方法施加,從而可以對土體施加小數值的固結壓力。
試驗所用土樣取自天津港,其液限為46 %,塑限為23 %,塑性指數為23。土樣的制作采用土膏法,初始含水率分別為88 %、96 %和117 %。
試驗采用一個土樣施加不同等級固結壓力的試驗方法,荷載等級為2.5 kPa、3.5 kPa、4.5 kPa、6.5 kPa、8.5 kPa、10.5 kPa、15.6 kPa和 20.7 kPa等。變形穩定的標準為每小時壓縮量小于0.01 mm。
1.2 試驗結果分析
小固結壓力作用下的固結試驗得到的孔隙比和固結壓力之間的關系如圖1所示。從圖中可以看出,吹填土在小固結壓力作用下的壓縮特性和常規固結壓力作用下的固結特性不同。當固結壓力小于10.5 kPa時,土體的孔隙比和固結壓力之間并不存在一一對應關系,而是和初始含水率有關,即含水率越大,在相同固結壓力作用下的孔隙比也越大。隨著固結壓力的增加,不同初始含水率土樣的孔隙比之間差值逐漸減小。當固結壓力超過10.5 kPa后,不同初始含水率的土體的孔隙比和固結壓力之間存在一一對應的關系,即和一般土體的固結特性相同。該結果表明,在小固結壓力作用下,吹填土存在一個臨界壓力,只有當固結壓力超過該臨界壓力后,它的孔隙比和有效應力之間才存在一一對應關系,而在此壓力之前孔隙比和固結壓力的關系與初始含水率有關。在本試驗中,臨界壓力為10.5 kPa。

圖1 吹填土壓縮試驗曲線
上述試驗結果表明,吹填土體的固結壓力和孔隙比之間的關系可以分為兩段,即:
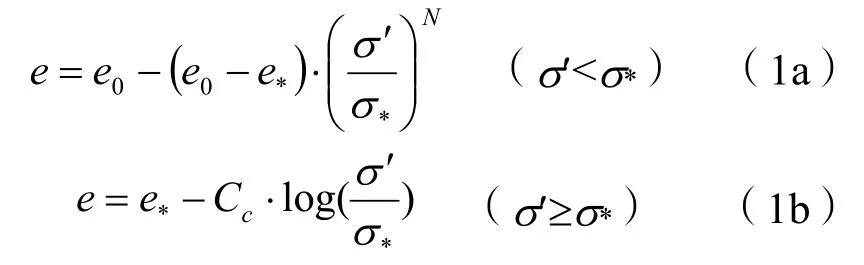
式中:e為孔隙比;σ′為固結應力;e0為初始孔隙比;σ*和e*分別為臨界壓力和該壓力所對應的孔隙比;Cc為壓縮指數;N為擬合參數。
圖1中給出了本次試驗三個土樣在0~σ*范圍內的擬合結果,其中N為 0.307,e*為 1.57,σ*為10.5 kPa,擬合結果和試驗結果非常接近。因此有:
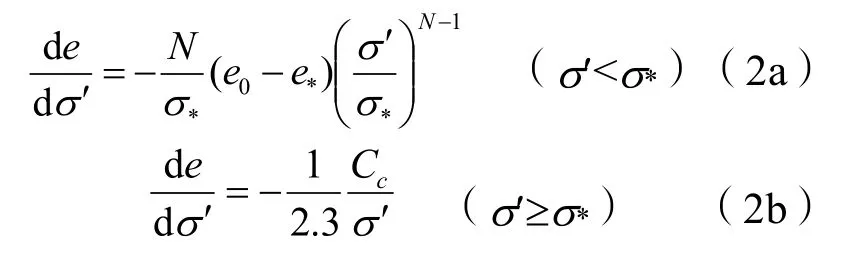
2 吹填土一維大變形固結理論
2.1 坐標系
在初始坐標系,即拉格朗日坐標系中,飽和軟黏土地基的初始坐標狀態如圖2(a)所示。在該坐標系中,地基表面為a=a0,不可壓縮層頂面為a=0。在該地基的坐標位置為a處取一微分體A0B0C0D0,其厚度為da,面積為1,孔隙比為e0。該地基在自重作用下固結,經過時間t后該地基在流動坐標中的狀態如圖2(b)所示。在該坐標系中,地基厚度變為z(a0,t),選取的微分體變為 ABCD,其坐標位置為z(a,t),厚度為dz,孔隙比為e,面積仍為1。根據微分體范圍內土顆粒重量在變形前和變形后相同的條件,可以得到:


圖2 固結理論坐標系
2.2 大變形固結方程
假定土體飽和,土顆粒和水不可壓縮,土體的壓縮和水的滲流只在豎向,且水和土顆粒的移動速度之差滿足達西定律,根據飽和土體的變形連續條件可以得到在流動坐標系下土體的固結方程為:
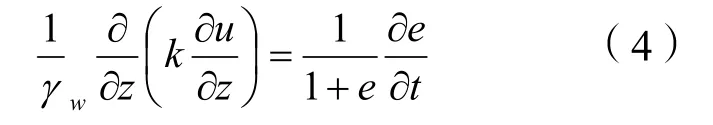
式中:u為超孔隙水壓力;γw為水的重度;k為滲透系數。
將式(3)代入式(4),可以得到在拉格朗日坐標系下的固結方程為:

對于圖2所示的地基,如果泥面保持在水位線以下,則根據有效應力原理可知,流動坐標系中位置為z處的有效應力為:

式中:γs為土顆粒的重度。
將式(6)代入式(5),可以得到:

式(7)即為拉格朗日坐標系下以超孔隙水壓力u為場變量的固結方程。
對于圖2所示的吹填土地基的重力固結問題,在初始坐標系下其邊界條件和初始條件分別為:

3 模型試驗及理論分析結果
3.1 模型試驗
為了研究表層有覆水情況下吹填泥漿在自重作用下的固結沉降過程。試驗用的模型槽為一1.5 m×1.5 m×1.5 m的鐵槽。試驗用的吹填土液限為44 %,塑限為27 %。吹填泥面初始的高度為1.35 m,平均含水量為180 %。
泥漿吹填后靜置,不經外界干擾,憑其自然固結,只是在試驗過程中將表層的水抽出一部分。因此,在固結過程中吹填泥漿表層一直有水覆蓋。在此過程中測量吹填泥漿表面的固結沉降量,直至泥面的沉降達到穩定。試驗時間約持續1年。
3.2 理論分析模型
本研究通過有限元方法求解式(7)及式(8a)、式(8b)來模擬分析上述模型試驗,其中,土體的比重取為 2.74,e0為 4.9,e*為 1.3,σ*為 10.5 kPa,N為0.2。
吹填土的滲透系數采用指數模型,即:
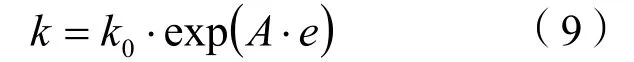
式中:k為滲透系數;k0和A為與土體塑性指數相關的擬合系數。根據滲透試驗結果,k0取為1.7×10-7cm/s,A為 1。
為了比較,本分析同時采用常規設計中的Terzaghi固結理論對該模型進行了固結分析,固結系數的取值為地基中間位置處在固結結束時應力狀態所對應的固結系數,即為0.0586 m2/Month。
3.3 分析結果
1)模型計算和試驗的沉降結果對比
泥面固結沉降隨時間變化的計算和試驗實測結果如圖3所示。圖3表明,泥面在固結開始時沉降速度很大,隨著時間的增加,沉降速度逐漸減小,計算結果在18.5個月時完全達到穩定值,最終沉降為 0.56 m。從圖中可以看出,實測的最終沉降為0.62 m,試驗結果和計算結果基本吻合,證明本計算結果的可靠性。

圖3 泥面沉降變化
2)超孔隙水壓力
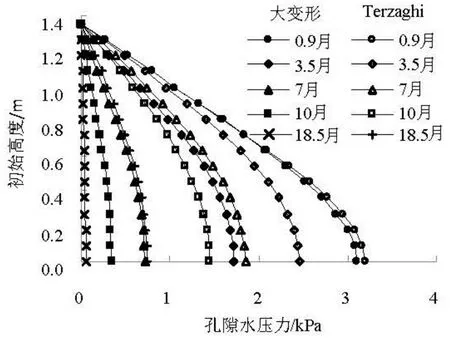
圖4 孔隙水壓力消散曲線
新吹填地基由于沒有經歷任何固結過程,其初始超孔隙水壓力沿高度的分布為一條直線,該直線的斜率為泥漿的有效重度。隨著固結時間的增加,地基中的超孔隙水壓力不斷消散,圖4為不同初始高度處超孔隙水壓力隨時間的分布。該結果表明,在泥面的頂部,超孔隙水壓力保持為 0,而泥面下的土體的超孔隙水壓力由于土體的固結而逐漸消散減小。從圖中可以看出,在相同的固結時間里,下部土體的超孔隙水壓力消散值大于上部土體的消散值,特別是地基底部的超孔隙水壓力降低值為最大,因此地基中超孔隙水壓力沿初始高度的分布曲線向內彎曲。隨著固結時間的增加,底部的超孔隙水壓力消散速度開始變慢,最后完全消散為 0。圖中數據表明,在18.5個月以后,地基的超孔隙水壓力基本消散完畢。
圖4同時繪制了常規Terzaghi固結理論計算得到的超孔隙水壓力分布。從圖中可以看出,當固結時間分別為0.9個月、7個月和18.5個月時,大變形固結理論計算得到地基底部的超孔隙水壓力分別為3.11 kPa、0.71 kPa和0.05 kPa,而Terzaghi固結理論計算得到的超孔隙水壓力分別為3.20 kPa、1.84 kPa和0.74 kPa。這表明,大變形固結理論計算得到的超孔隙水壓力消散的速度遠大于Terzaghi固結理論計算的結果。
3)固結度
圖5為分別根據泥面位移和超孔隙水壓力分布計算得到的平均固結度隨時間的變化過程。從圖中可以看出,一維大變形固結理論采用這兩種方法計算得到的固結度并不相同,采用位移表示的固結度要遠大于采用超孔隙水壓力計算得到的固結度,如當固結時間分別為0.9個月、7個月和18.5個月時,采用位移表示的固結度分別為 50.9 %、94.9 %和99.7 %,而采用超孔隙水壓力計算得到的固結度分別為7.8 %、78.2 %和98.5 %。這是由于土體的壓縮系數是一個不斷變化的參數,土體在固結的初始階段,由于土體的孔隙水壓力大,有效應力小,所對應的壓縮系數大,在消散相同的孔隙水情況下壓縮變形大;隨著超孔隙水壓力的消散,有效應力不斷增加,壓縮系數不斷減小,在消散相同的孔隙水情況下壓縮變形量逐漸減小。
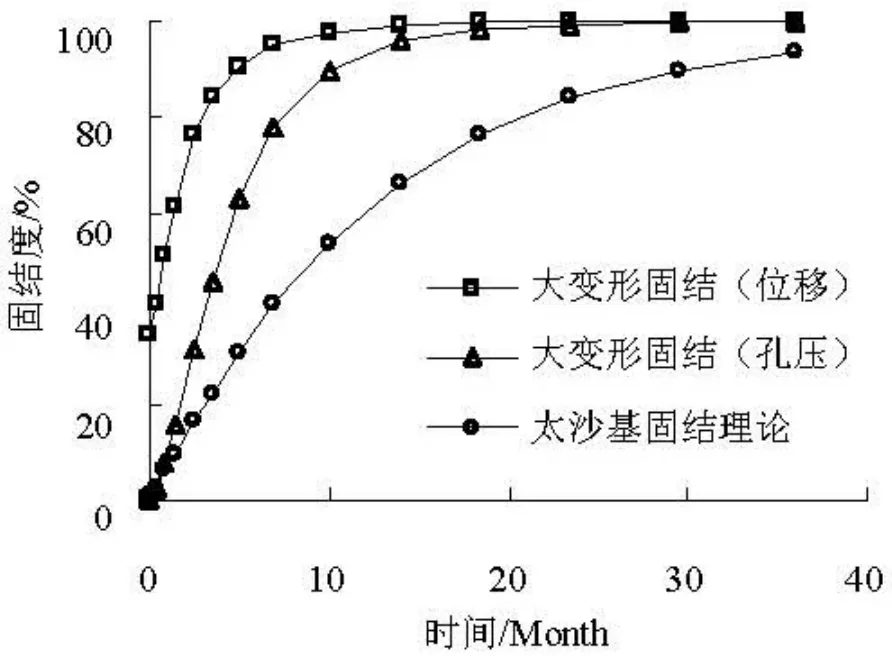
圖5 固結度比較
結果表明,吹填土在自重作用下的固結過程可以分為兩個階段。在開始階段,即對應于位移固結曲線中的7個月以前和超孔隙水壓力固結曲線的14個月以前,固結速度非常快。在隨后的固結過程中,地基的固結速度則非常緩慢。
從圖5由Terzaghi固結理論[13]計算得到的固結度變化曲線可以看出,Terzaghi固結理論計算得到的固結度遠小于大變形固結理論計算得到的結果。因此,Terzaghi固結理論將嚴重低估吹填泥漿地基的固結速度。
如果以不同位置處的超孔隙水壓力消散程度為該位置處的固結度,則可以得到不同高度處的固結度如圖6所示。從圖中可以看出,固結時間相同時,土體的固結度隨著高度的增加而減少,即底部土體的固結速度大于上部土體的固結速度。這個規律說明,雖然地基的排水面在泥面,但是在地基固結的初始階段,地基底部的超孔隙水壓力消散的速度較快,而頂部的超孔隙水壓力消散較慢。這主要是由于頂部的超孔隙水消散的比較小,因此其孔隙比變化小,滲透系數一直比較大,這有利于底部土體超孔隙水壓力的消散。

圖6 不同高度處的固結度
4 結 語
通過吹填土的室內小圍壓固結試驗,建立了吹填土的孔隙比和固結壓力之間的關系,并建立了以超孔隙水壓力為變量的一維大變形固結方程。通過對模型試驗進行一維大變形固結理論分析,得到如下結論:
1)吹填土體在小荷載作用下的壓縮特性和常規荷載作用下的壓縮特性不同。在小荷載作用下,吹填土的壓縮曲線存在一個臨界應力,當固結壓力小于該應力時,孔隙比和有效應力之間的關系與土體的初始孔隙比有關,只有大于該臨界應力時孔隙比和固結壓力的對數之間才是一一對應的線性關系。
2)吹填土自重固結過程中,當泥漿保持在水位以下時,底部的超孔隙水壓力和孔隙比降低較快,固結過程中上部土體的滲透系數大于下部的滲透系數,這有利于吹填土體中孔隙水向泥面排出。因此,固結時間相同時,底部土體的固結度比上部土體的固結度大。
3)按沉降計算得到的固結度大于按超孔隙水壓力消散程度計算得到的固結度。大變形固結理論計算得到的孔隙水壓力消散速度和固結度都遠大于常規Terzaghi固結理論計算得到的結果。因此,用Terzaghi固結理論計算吹填土在自重作用下的固結將嚴重低估吹填土的固結程度。

