基于動力學仿真的激光器平臺穩定性設計改進
胡杰
(1.中國工程物理研究院總體工程研究所,四川 綿陽 621999;2.工程材料與結構沖擊振動四川省重點實驗室,四川 綿陽 621999)
激光自誕生以來,在工程中得到了廣泛的應用,其傳輸、測量、瞄準應用過程中的穩定性問題是影響其精度的重要因素,也是工程中關注的重點。
影響激光器傳輸穩定性的因素有很多[1-3],大體上可分為兩個方面:一是激光自身,如波長不穩定和光強不穩定;另一方面則是其安裝平臺的結構穩定性。文中討論的是后者,主要考慮的是在外載荷作用下安裝平臺的位移變形對光學器件穩定性的影響,如安裝平臺的變形會導致激光器輸出功率大小出現不同程度的變化[4]。此外,在測量和瞄準等過程中,還會引起光學元件的漂移誤差等[5-6],嚴重影響精度。在我國ICF等大型光機裝置中,穩定性設計尤為重要。
在實際工程應用中,此類光學平臺在設計階段就需要通過數值模擬進行仿真,對穩定性進行評估。靜載荷(如過載、溫度)作用下,結構的變形是穩定的,對安裝平臺的穩定性評估也容易實現。如楊彬等[7]采用有限元方法模擬了不同螺栓預緊力作用下安裝板的變形情況。在動態載荷作用下,結構的位移響應也是動態的,其穩定性分析相對較為復雜。張軍偉等[8]針對某激光原型裝置,假設了每個光學元件對靶點定位影響符合高斯隨機分布,對光學元件的穩定性指標進行了分配。謝娜等[9]基于有限元數值模擬,分析了ICF裝置中某腔鏡組件的隨機振動響應,獲得了反射鏡的動態轉角。胡杰等[10]基于動剛度等效方法,對巨型光機結構鋼混結構平臺進行了動力學建模,數值模擬結果與實測值吻合較好,為穩定性分析提供了模型支撐。陳學前等[11]基于子結構分析技術,將整體結構中子結構連接界面的響應作為子結構的輸入載荷,然后僅針對子結構進行了動態響應分析,分析了地脈動作用下反射鏡片的轉角響應。
需要指出的是,上述分析中主要是以結構相對于基礎的位移響應作為穩定性評估參數。根據與設計方的討論,文中所研究的激光器平臺關注的是隨機載荷下,安裝平臺平板的相對變形情況,僅通過結構相對基礎的位移響應難以進行評估。因此在研究過程中,理論分析了平臺上兩關注點之間的相對位移關系,考慮了響應的隨機性以及相關性,該方法能夠更準確地評估平臺的穩定性。在應用研究中的結果表明,初始方案的平臺轉角響應不滿足設計指標要求,并通過動力學特性分析對設計方案進行了優化改進,有效降低了平臺轉角,滿足了設計指標。
1 隨機載荷下結構相對位移分析方法
記A和B點為結構上關注的兩個點,在隨機載荷作用下,其響應均是隨機變量,一般假定滿足正態分布。兩個關注點均包含x、y、z三個方向的自由度,記A、B點隨機振動下的x方向的響應分別為UAx、UBx。根據統計分析方法,A、B兩點之間x方向的相對變形D(Ux)計算公式為:

式中:D(UAx)和D(UBx)分別是A、B兩點x方向響應的方差;Cov(UAx-UBx)為A、B兩點隨機響應的協方差。
同理有A、B兩點之間的y方向和z方向的相對變形D(Uy)和D(Uz)的計算公式分別為:
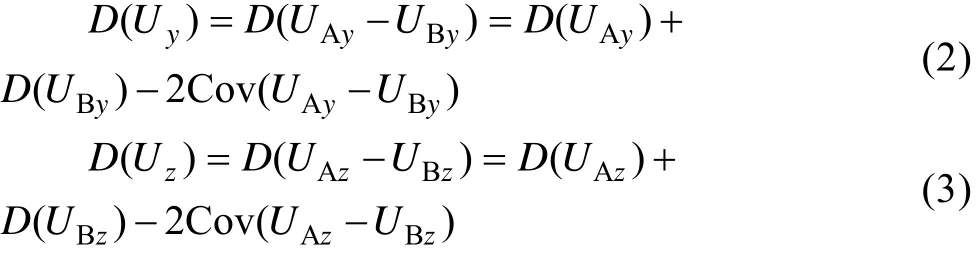
由上述相對位移分析可知,該公式考慮了兩個隨機變量之間的相關性,得到的相對位移反映了結構的彈性變形,因此能夠更準確地評估隨機振動條件下光學器件安裝平臺的變形情況。需要指出的是,隨機振動分析的計算結果需取3倍均方根值,以滿足99.73%的置信度。
2 激光器平臺模型
文中所研究的某激光器平臺初始方案幾何模型及方向定義如圖 1所示。該平臺尺寸為 870 mm×570 mm×203 mm,主體結構材料為鋁,光學器件通過質量等效建模,平臺通過底部12個螺栓安裝于整體結構中,設計指標為所關注的安裝平臺平板的角位移小于 10 μrad。

圖1 激光器平臺幾何模型Fig.1 Geometry model of laser-device platform:a) bottom; b) top
根據設計方要求,角位移的定義如圖2和式(4)所示
排料器的結構如圖3所示。其主要由滾筒、滑板、支撐輪等組成,滾筒與支撐輪相連,通過螺釘進行連接;滾筒和支撐輪沿周向皆均勻分布有12個細槽,且相對應地形成12個細長滑道;滑板位于滑道內,可上下運動。

式中:LAB為安裝平臺平板上點A和B之間的距離。
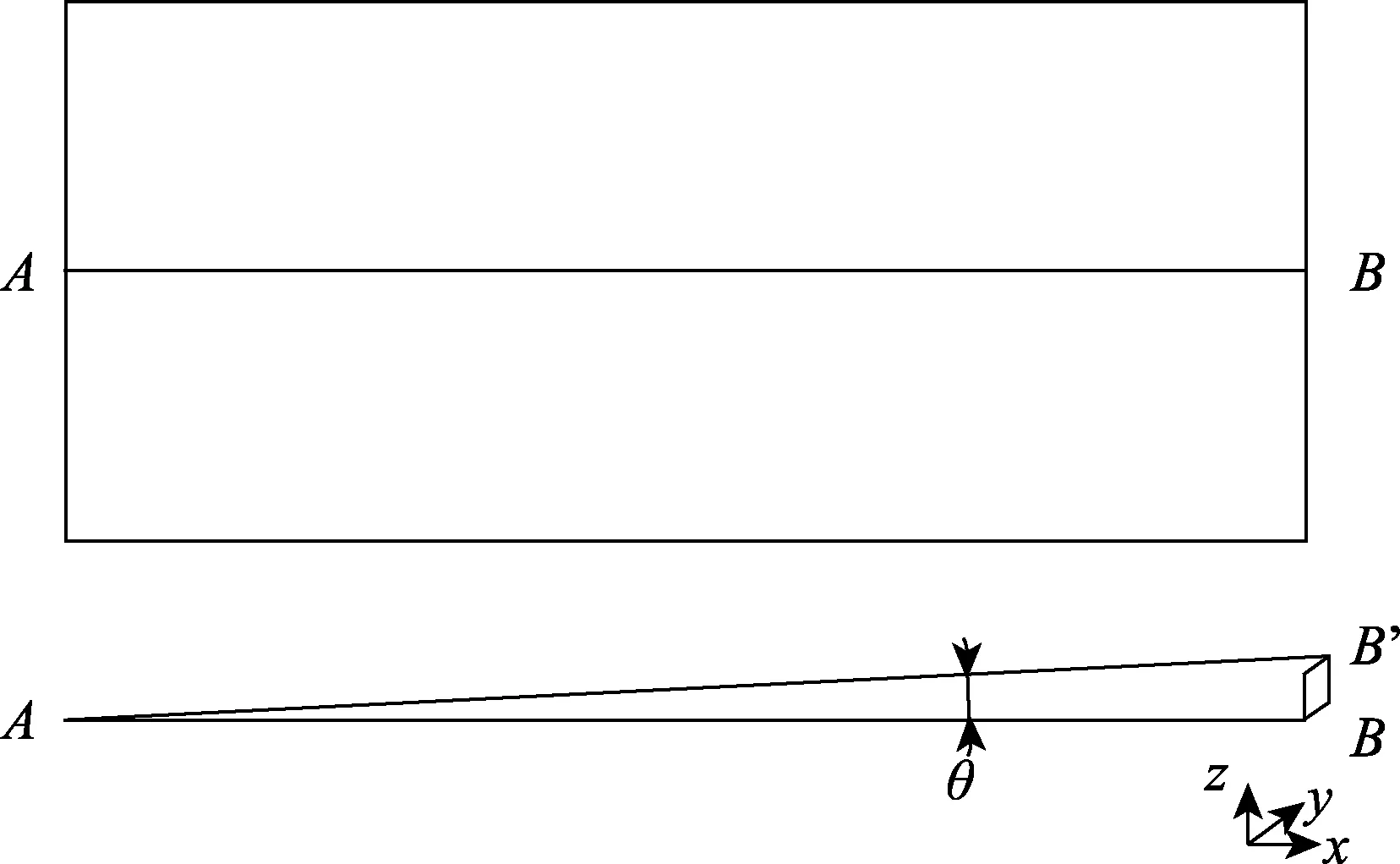
圖2 角位移定義Fig.2 Definition of angle displacement
邊界條件為底部12個螺栓連接有效接觸區域固支約束,隨機振動載荷條件見表1。
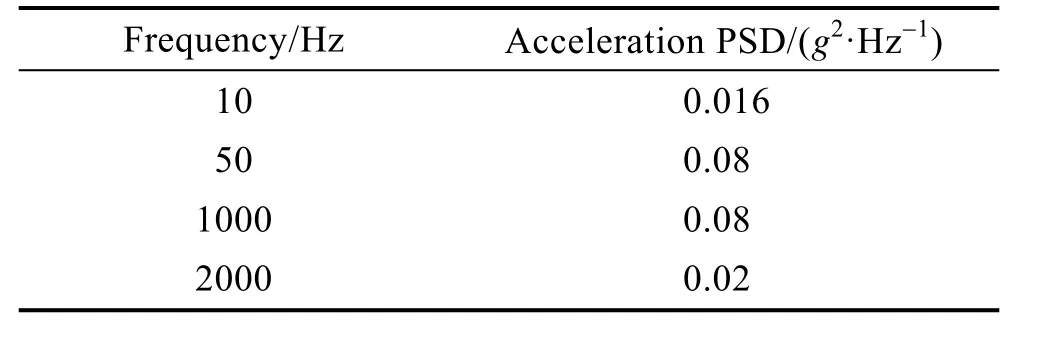
表1 基礎加速度載荷功率譜Tab.1 Power spectrum of foundation acceleration load
3 分析結果及方案改進
3.1 初始方案分析
通過對初始方案的數值模擬,得到各響應參數見表2。

表2 初始方案位移響應(倍均方根值)Tab.2 Displacement response of initial scheme(root mean square value) mm
再根據式(2)、(3)、(4)計算得到平臺平板的角位移為26.6 μrad,不滿足設計指標要求。通過對結構模態特性的分析,觀察到安裝平臺的前幾階振型如圖3所示。可以看出,點A和B所在位置變形較大,這是由于A點和B點在平臺短邊上,剛好處于近似兩端固支結構的中間,為低階彎曲模態變形較大的位置(如圖 4所示),而低階模態對結構的動態位移響應影響較大,因此造成 A、B點的動態響應較大。
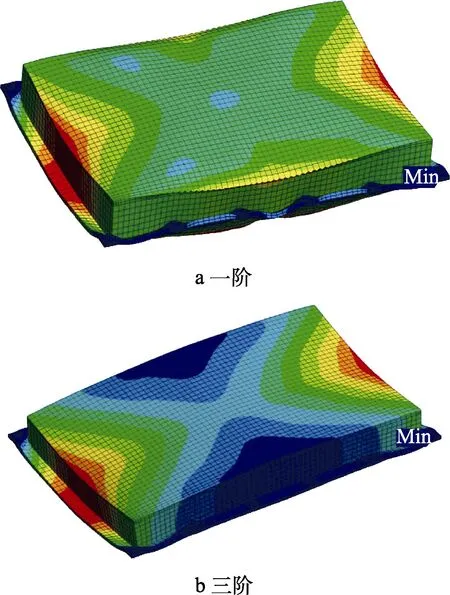
圖3 安裝平臺低階模態振型云圖Fig.3 Low order mode shape of platform mounting:a) first order; b) third order
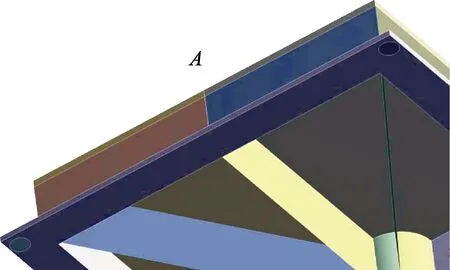
圖4 點A所處位置示意Fig.4 Position of point A
3.2 改進方案及分析
根據初始方案不滿足設計指標的原因分析,針對性地對安裝平臺的裝配方式進行了改進,如圖 5所示,即在A和B點的下方增加一個螺栓約束。
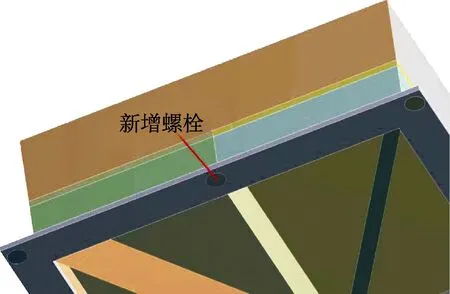
圖5 新增螺栓位置示意Fig.5 Position of newly increased bolt
改進方案的低階振型云圖見圖6,與圖3相比,A、B位置的低階模態振型的變形明顯減小,得到計算平臺角位移過程中的各項參數值見表3。計算得到平臺的角位移為3.4 μrad,得到大幅度減小,滿足設計指標要求。
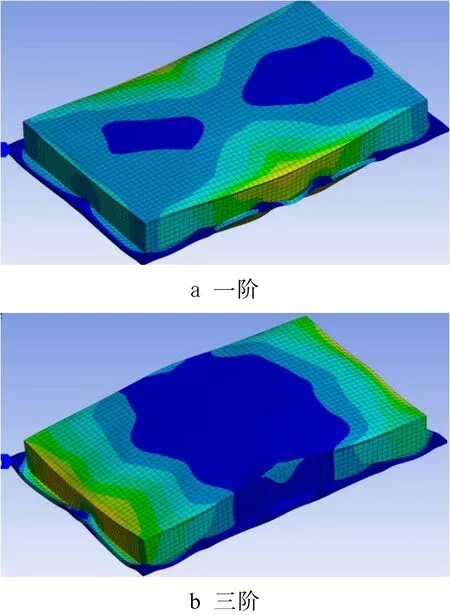
圖6 改進方案安裝平臺低階模態振型云圖Fig.6 Low order mode shape of improved platform mounting: a) first order; b) third order
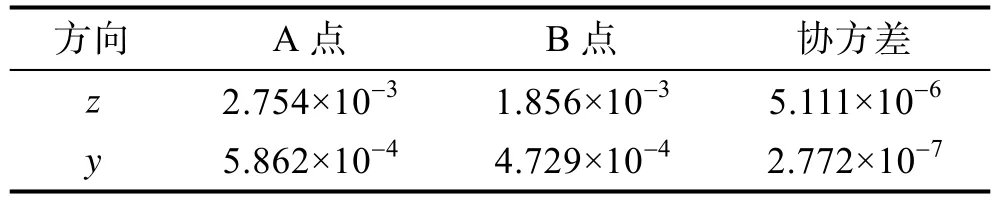
表3 改進方案位移響應(倍均方根值)Tab.3 Displacement response of improved scheme(root mean square value) mm
3.3 進一步的討論
雖然改進方案已經滿足設計指標要求,但進一步深入考慮,光學平臺結構的穩定性實質上是盡可能減少平臺的彈性變形,即希望平臺有足夠的平整性。本項目中,根據設計方要求,只是從A、B兩點的相對變形來評估平板的角位移,而平板中部的變形情況未考慮。因此,為減小整個平臺的變形,可在安裝平臺底板中部再增加約束,如圖7所示。
圖7 安裝平臺底部中部新增約束示意Fig.7 Position of new restraint at the middle bottom of platform
初始方案、改進方案、中部新增約束方案三種設計下平臺平板的法向變形如圖8所示。可見平板上的最大位移響應(三倍均方根值)分別為0.25、0.21、0.15 mm,逐次顯著減小,說明整個平臺的平整性得到逐步提高,更有利于提高安裝平臺的穩定性。

圖8 三種方案安裝平臺平板的變形Fig.8 Deformation of platform mounted through three schemes: a) original design; b) improved design;c) new restraint scheme in the middle
中部新增約束方案角位移過程中的各項參數見表4。得到安裝平臺角位移為3.6 μrad,與改進方案差別不大,但兼顧了整個平臺的平整性。

表4 中部新增約束方案位移響應(倍均方根值)Tab.4 Displacement response of new restraint scheme in the middle (root mean square value) mm
4 結論
通過以某激光器平臺的穩定性分析及設計方案改進研究為例,可以得到如下結論。
1)光學平臺結構的彈性變形是影響平臺穩定性的主要因素。
2)隨機振動條件下,光學平臺的穩定性分析需要重點關注相對位移變化,尤其需要考慮關注點響應之間的相關性。
3)從結構動力學特性來分析結構的響應規律,進而指導設計方案的改進。
4)光學平臺結構的穩定性評估應當從整個平臺變形情況來考慮,僅僅幾個點的比較分析還不夠全面。

