世錦賽視角下男子田賽跳躍類項目發展與成績預測研究

郭樹君，曹 杰

世界田徑錦標賽(以下簡稱世錦賽)自1983年舉辦以來，極大地推動了世界各國田徑運動的發展。筆者統計了中國代表隊在12-16屆中的表現，跳躍類項目積39分，而投擲類項目積0分，跳躍類項目發展遠勝于投擲類項目發展。研究世錦賽田賽跳躍類項目運動成績，一方面可以使我們了解當今世錦賽田賽跳躍類項目發展水平，另一方面也能了解我國男子田賽跳躍類項目到底處在什么樣的一種發展水平。因此研究世界田徑錦標賽男子田賽跳躍類項目的發展顯得頗為重要。黃海平、曲淑華、車超主要通過平均遞進系數、標準差和平均值等統計學指標去反映運動成績的走向。曲淑華、王秀軍運用灰色系統理論建立GM(1,1)模型去預測世錦賽奪冠成績，而這種模型需要的樣本數據比較少，且局限性少，計算簡便，檢驗方便。本文則是從平均值、遞進系數和標準差三個研究指標去描述世錦賽男子田賽跳躍類項目運動成績發展，通過建立GM(1，1)模型并利用matlab數學建模軟件實現2021年第18屆世錦賽的成績預測。

1 研究對象與方法

1.1 研究對象

以第1-17屆世界田徑錦標賽田賽跳躍類項目(跳遠、三級跳遠、跳高、撐竿跳高)前八名運動員運動成績為研究對象。

1.2 研究方法

1.2.1 文獻資料法

訪問國際田聯官方網站，獲得第1-17屆(1983年第1屆-2019年第17屆)世界田徑錦標賽男子田賽跳躍類四個項目(跳遠、三級跳遠、跳高、撐竿跳高)前八名運動員成績。訪問中國知網，以“世界田徑錦標賽”、“發展”、“成績預測”等關鍵詞進行檢索，整理匯總與本論文研究內容相關的資料。

1.2.2 數理統計法

使用Word統計出每屆各項目第一名成績、前三名的平均成績、前八名的平均成績、前八名成績的標準差。采用遞進系數公式，D=(X-Y)/Y×100 (D遞進系數;X本屆世錦賽前8名平均成績;Y前一屆世錦賽前8名平均成績)，反映田徑項目總體的發展趨勢。

1.2.3 比較分析法

對第1-17屆世錦賽標田賽項目男子跳躍類項目進行橫向縱向比較分析。

1.2.4 灰色預測法

運用 GM ( 1，1 )灰色預測模型思想，利用數學建模Matlab軟件分析，預測2021世錦賽男子田賽跳躍類項目第一名的成績。

2 研究結果與分析

2.1 田徑世錦賽男子田賽跳躍類項目發展態勢分析

2.1.1 世錦賽男子跳遠項目成績變化特征分析

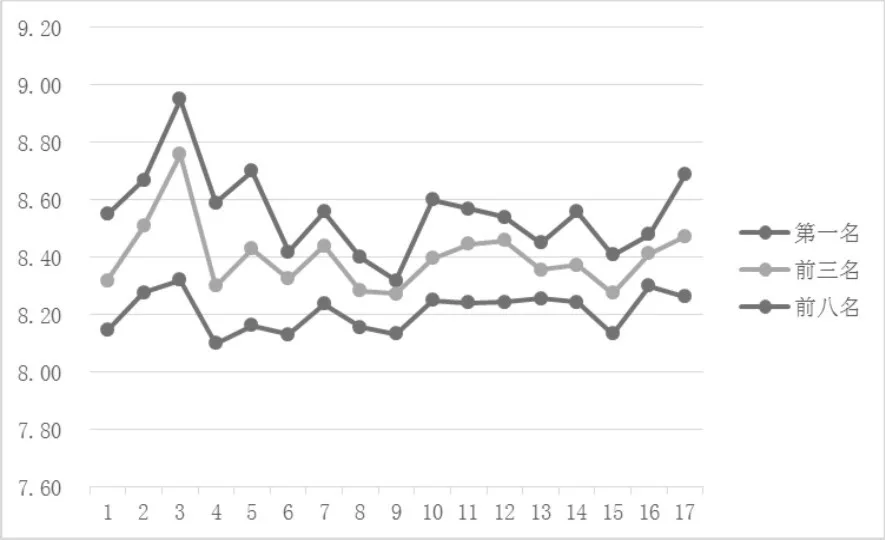
圖一 歷屆世錦賽跳遠項目前八名運動員成績曲線(單位:m)

歷屆世錦賽男子跳遠奪冠成績在第3屆取得最高值,成績為8.95m，在第9屆取的最低值，成績為8.32m。整體成績也在第三屆取得最高值，成績為8.32m,在第四屆取得最低值，成績為8.10m，差值為0.22m。自第3屆美國選手Mike powell創造出8.95m的世界紀錄以來，跳遠項目發展緩慢，之后的歷屆成績距離世界紀錄的差值最小為0.25m，仍有較大差距，短時間內沒人能突破這個成績。整體的發展趨勢為：1-3屆逐步發展高峰期，4-9屆處于低谷期，10-14屆穩定期，15-17處于暫時的波動期，整體呈現穩定的緩慢上升趨勢。

第1-17屆世錦賽男子跳遠前8名運動員平均成績的遞進系數均值為0.10，說明整體上男子跳遠項目成績呈現上升趨勢。第1、3、6、9、14、15個遞進系數絕對值相對較大，表明第1-2、3-4、6-7、9-10、14-16屆平均成績波動較大；第10、12、13、14、16屆運動員整體水平較高且標準差相對較小，可知第10、12、13、14、16屆男子跳遠項目競爭的確激烈。

總的來說：世錦賽跳遠項目經歷了短時間的增長和較長時間的低谷和平穩發展，總體呈緩慢波動上升的一個趨勢。

2.1.2 田徑世錦賽男子三級跳遠項目成績變化特征分析

歷屆世錦賽三級跳遠奪冠成績在第5屆取得最高值,成績為18.29m，在第1屆取的最低值，成績為17.42m,差值為0.87m；平均成績在第13屆取得最高值，成績為17.46m,在第1屆取得最低值，成績為17.09m，差值為0.37m，差值較大受到第一屆成績影響。自從第五屆世錦賽英國選手jonathan Edwards創造世界紀錄18.29米以來，只有兩人闖進18.00m，分別為15屆美國選手christian Taylor的18.21m和14屆法國選手teddy Tamgho的18.04m，間接表明三級跳遠發展緩慢。整體的趨勢為：除首屆以外，整體平均成績在17.20-17.40之間波動，第2-12屆波動較小，13-17屆波動較大，整體成績呈現穩定的緩慢增長趨勢。

第1-16屆世錦賽男子三級跳遠前8名運動員平均成績的遞進系數均值為0.14，說明整體上男子三級跳遠項目成績呈現上升趨勢。第1、12、13、16個遞進系數絕對值較大，表明第1-2、12-14、16-17屆成績波動較大；第2、4、6、13屆運動員整體水平較高且標準差相對較小，可知第2、4、6、13屆男子三級跳遠項目競爭的確激烈。

總的來說：三級跳遠項目整體成績經歷了穩定的慢增長和慢下降交替，成績波動較小過渡到波動較大，總體呈現緩慢波動上升的趨勢。

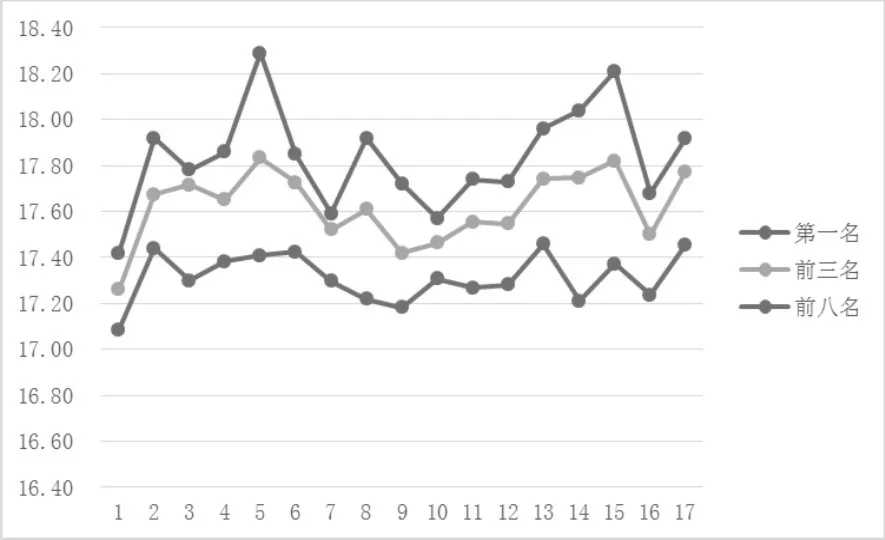
圖二 歷屆世錦賽三級跳遠項目前八名運動員成績曲線(單位:m)

2.1.3 田徑世錦賽男子跳高項目成績變化特征分析

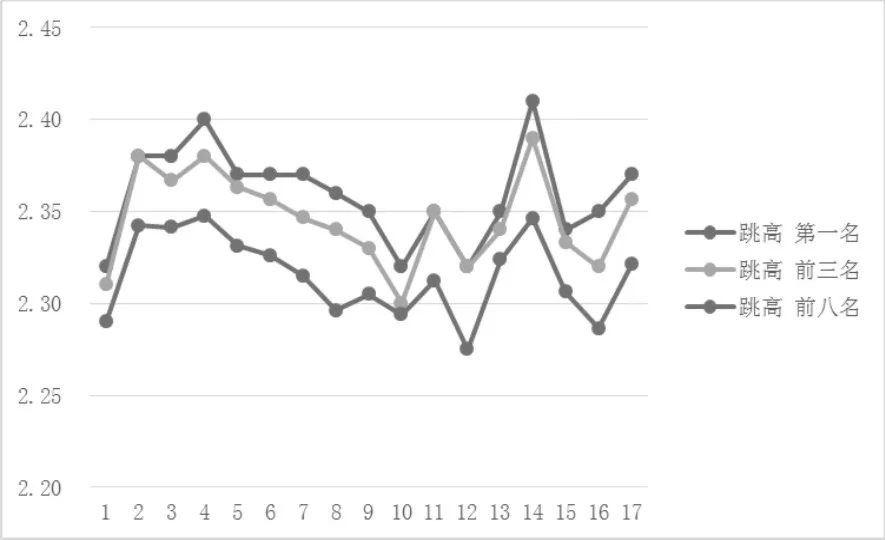
圖三 歷屆世錦賽跳高項目前八名運動員成績曲線(單位:m)

歷屆世錦賽跳高奪冠成績在第14屆取得最高值,成績為2.41m；在第1屆取的最低值，成績為2.31m,差值為0.10m，成績較為穩定平均成績在第4屆取得最高值，成績為2.35m,在第12屆取得最低值，成績為2.28m，差值為0.08m。整體的趨勢為：1-4屆到達高峰，5-12屆逐漸下降到最低值，13-14屆上升到最高峰，15-16屆大幅下降，17屆大幅上升的局面。

第1-17屆世錦賽男子跳高前8名運動員平均成績的遞進系數均值為0.09，說明整體上男子跳遠項目成績呈現上升趨勢。第1、11、12、14、16個遞進系數絕對值較大，表明第1-2、11-13、14-15、16-17屆成績波動較大。第3、4、6、13屆運動員整體水平較高且標準差較小，可知第3、4、6、13屆男子跳高項目競爭的確激烈。

總的來說：跳高項目整體發展經歷了短時間的增長，再到長時間的穩定下降，再到短時間的增長和下降的局面。

2.1.4 田徑世錦賽男子撐竿跳高項目成績變化特征分析

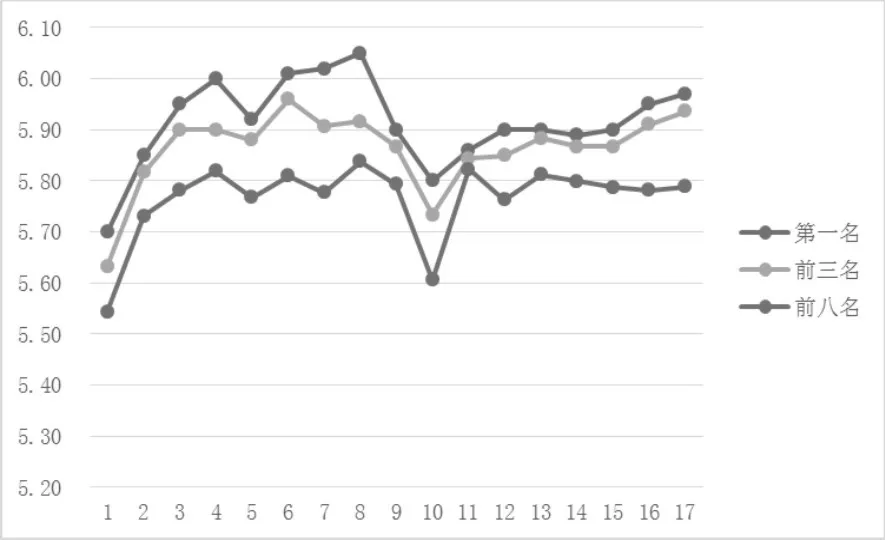
圖四 歷屆世錦賽男子撐竿跳高項目前

歷屆世錦賽男子撐竿跳高奪冠成績在第8屆取得最高值,成績為6.05m，在第1屆取的最低值，成績為5.70m,差值為0.35m，奪冠成績從1-8屆發展迅速，9-10屆跌入低谷，11-17屆穩步發展；平均成績在第8屆取得最高值，成績為5.84m,在第1屆取得最低值，成績為5.54m，差值為0.30m。整體的趨勢為：除了第1、10屆成績較低外，整體平均成績在5.80左右起伏的局面。

第1-17屆世錦賽男子撐竿跳高前8名運動員平均成績的遞進系數均值為0.28，說明整體上男子撐竿跳高項目成績呈現上升趨勢；第1、7、9、10、11遞進系數絕對值較大，表明第1-2、7-8、9-12屆成績波動較大。第4、8、9、11、13、14、15屆運動員整體水平較高且標準差相對較小，可知第4、8、9、11、13、14、15屆男子跳高項目競爭的確激烈。

總的來說：撐竿跳高項目除了第1、10屆整體成績穩定在5.80左右，呈現穩定的緩慢上升趨勢。

2.2 2021年第18屆世錦賽田賽項目第一名成績預測

本文則是用觀察到的反映世錦賽田賽跳躍類項目成績特征的時間序列來構造灰色預測模型，預測下一屆世錦賽田賽跳躍類項目成績特征。使用鄧聚龍教授提出的均值GM(1,1)灰色模型(EGM模型較其它模型適用于振蕩序列)，對第17屆世錦賽男女子田賽項目第1名成績進行建模預測分析。(X(0)為預測序列，x(0)為實際序列)。

以男子跳高項目為例，統計近五屆世錦賽男子跳高項目第一名成績，運用均值GM(1,1)灰色模型對第18屆世錦賽男子項目第1名成績進行預測:

第一步：獲取第13屆至17屆世錦賽男子跳高項目第一名成績作為原始序列，x(0)(k)=[2.35,2.41,2.34,2.35,2.37];

第二步：對原始數據進行一次累加，得到一次累加序列，

x(1)(k)=[2.35,4.76,7.10,9.45,11.82];

第三步：對累加序列進行緊鄰均值生成，得到緊鄰均值序列，

z(1)(k)=[3.5550,5.9300,8.2750,10.6350];

第四步：用最小二乘法對參數向量A進行估計，其中A=(BTB)-1BTY；運用matlab軟件計算求得，發展系數 a=0.0047，灰色作用量 b=2.4007；

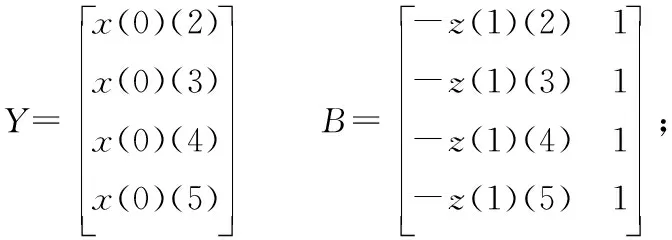
第五步：均值GM( 1，1)模型的時間響應式為: X(1)(k) =[x(0)(1)- b/a] e-ak+b/a，即X(1)(k)=-508.4372e-0.0047k+510.7872；

第六步：按 X(0)(k)=[X(1)(k)-X(1)(k-1)]，k=2，3，4，5 ，將預測數據還原，計算出預測值X(0)(2) =2.3841,X(0)(3)=2.3730,X(0)(4)=2.3619，X(0)(5)=2.3509。

第七步:采用相對誤差法去檢驗模型精度。

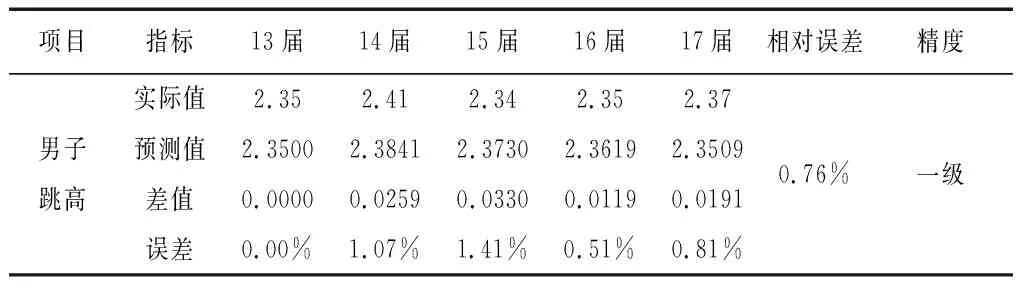
表1 近五屆世錦賽男子跳高項目相對誤差表

本文的模擬值與原始值的平均相對誤差為0.76%，小于1%，模擬的精度為一級，所以從這一方面考慮，本文相對模擬誤差較小，精度較高，模型較好，能夠較好地預測第 18屆世錦賽男子跳高成績。

第八步: 根據預測模型，計算得第 17屆世錦賽女子鉛球第1名成績預測值為X(0)(6) = 2.3399，即預測值為2.34m。

根據上述分析步驟，預測其他三個項目的冠軍成績，其中跳遠誤差0.84%、三級跳遠誤差0.66%、跳高誤差0.76%、撐竿跳高0.09%，相對誤差均小于1%，預測模型的成績精度均在一級以上，模擬的預測數據較好。根據數據顯示，第18屆世錦賽田賽跳躍類項目的奪冠預測成績分別為：男子跳遠8.65m、男子三級跳遠17.74m、男子跳高2.34m、男子撐竿跳高6.00m.

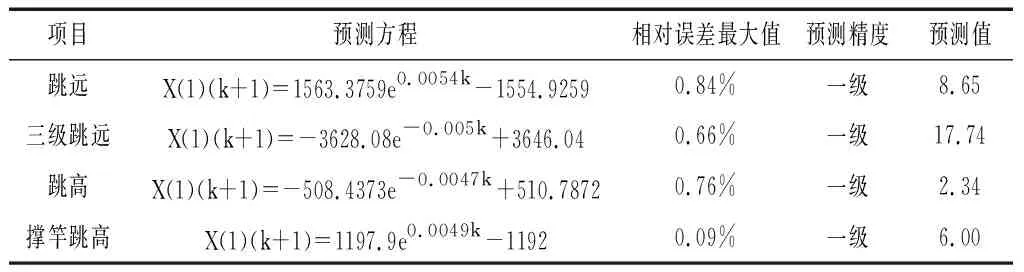
表2 男子田賽跳躍類項目預測方程精度與預測成績值(單位：m)

2.3 我國男子田賽跳躍類項目發展態勢

2.3.1 我國男子跳躍類優秀運動員基數小

目前，還未有中國人在男子田賽跳躍類項目中獲得金牌，獲得獎牌的相對也較少。朱建華在第一屆世錦賽以2.29m獲得第三名；張國偉在第15屆世錦賽上以2.33m獲得第二名。王嘉男在第15屆世錦賽以8.18m獲得第三名。獲得前八名名次的有12人，其中跳遠8人、跳高2、撐竿跳高1人、三級跳遠1人，前八名以外的名次有16人，三級跳遠5人、跳高4人、撐高跳高4人、跳遠3人。說明了我國男子田賽跳躍類優秀運動員基數小。

2.3.2 我國田賽跳躍類項目的發展情況為：跳遠>跳高>三級跳遠>撐竿跳高

總的來說，跳遠項目發展最好，跳高項目較好，三級跳遠次之，撐竿跳高最后。

2.3.3 我國田賽跳躍類項目呈現短期的同步發展

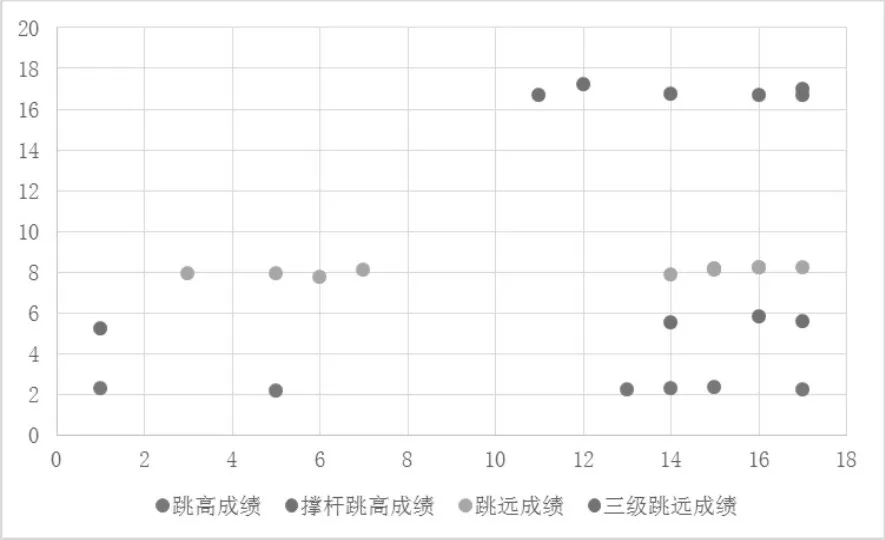
圖五 歷屆男子田賽跳躍類項目運動成績散點圖

我國田賽跳躍類項目的發展隨著歷屆世錦賽的發展逐漸呈現出穩定的發展態勢，自第14屆世錦賽之后，我國田賽四個跳躍類項目歷屆挺進世錦賽人數增多，出現了短期上項目同步發展。相對于14屆之前，我國的四個項目從未有過同步發展，只有跳遠項目有過短時間的發展；而跳高、撐竿跳高、三級跳遠項目發展落后，停滯不前。

2.3.4 我田賽跳躍類項目發展從“無法踏入世錦賽”到“能夠踏入卻無法取得優秀成績”轉變

近年來我國世錦賽男子田賽跳躍類項目的整體發展現狀已經從大部分項目無法踏入世錦賽的大門轉變到有能力踏入

世錦賽的大門但無法獲得較高的運動成績的轉變，可見近幾年我國田賽跳躍類項目發展有所建樹，但是如何提高現有的水平，沖擊更高的成績和排名仍然需要運動員和教練員等多方面的努力。

3 結論

3.1 世錦賽田賽跳躍類項目發展態勢

世錦賽田賽跳躍類四個項目整體水平呈現緩慢上升態勢。跳遠項目整體的發展趨勢為：1-3屆逐步發展高峰期，4-9屆處于低谷期，10-14屆穩定期，15-17處于暫時的波動期；三級跳遠項目整體的發展趨勢為：除首屆以外，整體平均成績在17.20-17.40之間波動，第2-12屆波動較小，13-17屆波動較大；跳高項目整體的趨勢為：1-4屆到達高峰，5-12屆逐漸下降到最低值，13-14屆上升到最高峰，15-17屆波動下降的局面；撐竿跳高項目整體的趨勢為：除了第1、10屆整體成績穩定在5.80左右，呈現穩定的緩慢上升趨勢。

3.2 2021年第18屆世錦賽田賽跳躍類項目預測值

第18屆世錦賽田奪冠預測成績分別為：男子跳遠8.65m、男子三級跳遠17.74m、男子跳高2.34m、男子撐竿跳高6.00m。

3.3 我國男子田賽跳躍類項目發展態勢

我國男子田賽跳躍類優秀運動員基數小，項目的發展情況表現為：跳遠>跳高>三級跳遠>撐竿跳高，近幾年我國田賽跳躍類項目呈現短期的同步發展，已從“無法踏入世錦賽”到“能夠踏入卻無法取得優秀成績”轉變。