基于蟻群算法的湛徐高速公路中長期養護費用分配分析

劉躍生

(廣東能達高等級公路維護有限公司，廣東 廣州 510030)

公路養護是確保公路長期穩定運營的關鍵。隨著運營車輛的逐日增多，公路病害越來越多，養護頻率和養護費用增加。當前公路養護決策者“重建輕養”，道路養護也未形成系統、科學的方法，工程師經驗往往影響養護頻率及養護效果，很難使養護費用得到高效的養護結果。加上公路養護的定額費用年度分配不合理，不能有效解決公路病害，因而很難進行全路段養護。對公路養護費用進行科學分配，可優化養護費用分配方法，獲得最優養護效果，還可通過養護費用分配模式動態了解公路運營狀況，方便制定科學的決策計劃。國內學者提出了一些費用分配方法，建立了費用分配模型，如基于模糊推理的智能資金分配模型、動態規劃法下養護費用單目標優化分配模型、單年度資金優化分配模型、基于α-魯棒的公路養護費用分配模型、蟻群算法養護模型等。其中蟻群算法可對路面狀態進行識別，有針對性地分配養護費用，避免各路段平均分配養護費用等不合理現象。該文針對湛徐(湛江—徐聞)高速公路路面養護，基于蟻群算法構建養護費用分配模型進行中長期養護費用分配。

1 中長期養護費用分配模型及思路

1.1 公路多年度分配模型

路面養護費用并非每年固定不變，需結合路面性能狀態進行分配。為合理獲得各年度養護費用大小，建立多年度費用分配模型。建模時需考慮以下幾點：1) 設定一個養護規劃期，可以是5、10年等；2) 設定養護資金及反映路面性能的指標作為約束水平；3) 采用灰色GM(1,1)模型對各年度路面性能指標進行預測；4) 采用蟻群算法結合MATLAB編程求解。

根據以上要求，選擇5年中長規劃期，基于路面狀況，收集多個預測數據，設置路面損壞狀況指數PCI及費用兩個約束條件進行規劃期內各年度養護費用分配，通過蟻群模型反復計算，獲得滿足約束條件的各年度養護費用分配結果。各年度以PCI為約束條件的費用分配計算式如下：

(1)

其他約束條件：

(2)

(3)

(4)

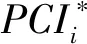
PCI按下式計算：

PCI=100-a×DRb

(5)

式中：a、b為系數；DR為路面綜合破損率，DR=D/A×100；A為路面總面積。

對2014—2015年湛徐高速公路路面PCI值與DR的關系進行回歸，得到a=15、b=0.412。采用蟻群算法進行關鍵指標求解，求解過程如下：1) 讀入路段數據；2) 將數據初始化；3) 設置信息素濃度；4) 迭代次數加1；5) 進行螞蟻k=0計算；6) 進行螞蟻k=k+1計算；7) 隨機給定第一個節點參數；8) 選擇節點；9) 按照轉移概率選擇另外一節點；10) 若全部節點操作完畢，進入下一步，否則返回步驟8；11) 求解適應度，更新信息素；12) 若全部螞蟻操作完畢，則進入下一步，否則返回步驟6；13) 若達到迭代次數，則輸出結果，否則返回到步驟4。

1.2 養護費用分配思路

(1) 將養護費用均分為5等份，養護規劃年度內各一份，再結合路面病害類型進行養護費用分配。

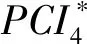
(7) 比較5年規劃期內PCI值，若滿足設置的PCI值要求，則費用分配結果為最優，否則再次對養護費用進行各年度分配并計算各年度的PCI值，直至其滿足約束要求為止。如此反復計算，獲得最佳養護費用分配方案。

2 湛徐高速公路中長期養護費用分配

2.1 湛徐高速公路概況

湛徐高速公路為(沈陽)同江至(海南)三亞國道主干線中的粵境路段，主線長114.302 km，2010年正式通車，運營一段時間后出現各種路面病害，相關部門每年均安排養護資金進行路面維護。為分析方便，選擇其中一段近幾年的檢測數據、路面破損狀況及修復資金作為其后期養護費用分配的基礎數據。湛徐高速公路部分路段近5年路面狀況指數見表1，基年路面破損狀況見表2。

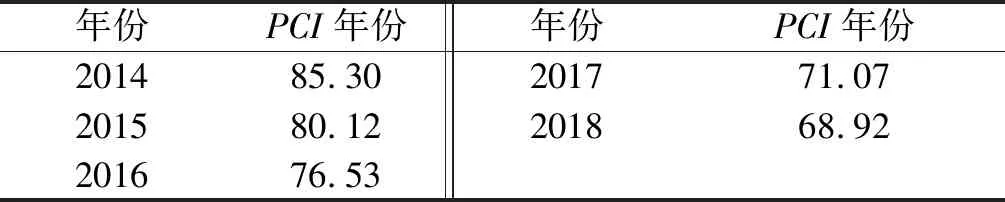
表1 湛徐高速公路部分路段近5年路面狀況指數

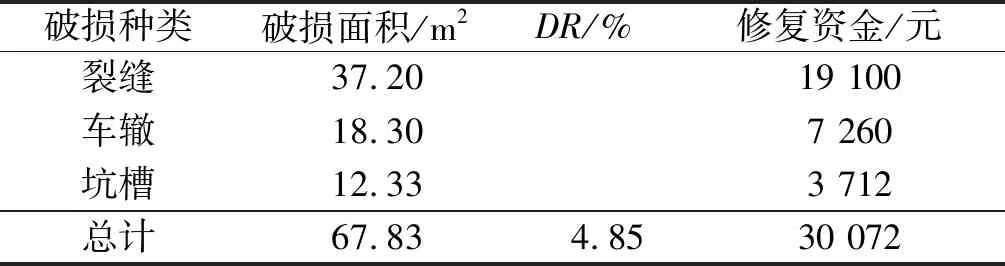
表2 湛徐高速公路部分路段基年路面破損狀況

由表2可知：基年內各類破損的全部維修費用為30 072元，將其定為維修資金額度，作為后續維修費用分配的基礎。采用蟻群算法，建立相關約束條件，以目標路段PCI指數的平均值為目標進行有限養護費用年度優化分配。

2.2 費用分配約束要求

基于基年內公路現狀選擇5年規劃期進行費用分配。該項目為瀝青路面，在基年破損基礎上進行養護，運營一段時間后其性能逐步降低，尤其是車輛荷載增多后，路面性能下降更明顯，需針對病害特點及時進行修復。由于路面養護費用有限，若現有養護費用得不到科學分配，則很難維持路面性能。為此，設置兩種費用約束水平(見表3)，基于固定的養護費用，對5年規劃期內年度養護費用進行分配，通過不同年度養護費用的投入獲得5年規劃期內滿足一定約束條件的路面狀況。

表3 規劃期內費用分配約束水平

2.3 中長期養護費用分配

2.3.1 水平1約束下養護費用分配

水平1約束下費用較充足，考慮到基年內養護費用較高，若按照基年修復標準，則規劃期內后幾年養護費用基本上分配不到，故將養護費用標準提高到32 000元；同時要求規劃期內PCI值均大于90。將以上約束條件代入蟻群算法中進行計算，經過300次進化代數后的PCI均值見圖1。

圖1 水平1約束下蟻群算法運算后的PCI均值

由圖1可知：在運算初期，PCI值為89.6；隨著進化代數的增大，PCI值增大，進化代數達到180次左右時PCI值趨于穩定，為92.8左右，可認為PCI=92.8為蟻群算法最優解。對應的5年規劃期內養護費用分配結果見表4，表4養護費用分配情景下5年規劃期內路面狀況指數見表5。

表4 水平1約束下各規劃年度養護費用分配結果

表5 水平1約束下各規劃年度養護后的PCI值

由表4可知：水平1約束下，養護費用較充足時，第1年規劃內養護費用分配值最大，占整個養護費用的93%左右；其余4年的養護費用均較小，且相差不大。

由表5可知：第1年養護后PCI值為93.76，DR值僅為0.1，滿足表2中約束要求；隨后4年的PCI值逐漸減小，但均大于90，滿足約束要求。

造成以上養護費用分配差異大的原因是基年內路面病害多，養護工作量大，通過分配較多的養護費用使路面PCI值達到既定要求后，后續規劃年內的養護工作量不大，因而維持較高路面質量所需養護費用較少。該費用分配結果與實際養護費用分配情況相符。

在費用較充足的水平1下進行蟻群算法分析，可獲得與實際相近的費用分配結果。但蟻群分配計算較粗糙，可結合實際經驗進一步精確。

2.3.2 水平2約束下養護費用分配

水平2約束下養護費用偏緊，同時PCI值達到表2中要求。考慮到基年內維修費為30 072元，在費用偏緊情況下設置30 000、28 000、25 000元3種養護費用，采用蟻群算法建立模型，計算3種養護費用下5年規劃期內費用分配和對應的PCI值。計算中為追求費用分配最大效益，使各年度路面PCI均值最大，同時確保對應的PCI最小值盡可能大。水平2約束下養護費用分配結果及PCI值計算結果分別見圖2、圖3。

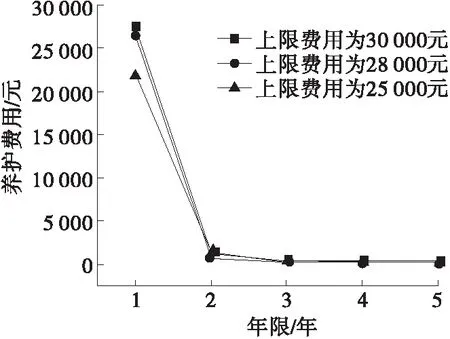
圖2 水平約束2下各規劃年度養護費用分配結果

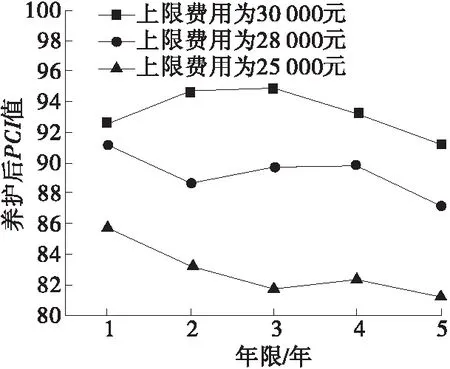
圖3 水平約束2下各規劃年度PCI值

由圖2、圖3可知：不同上限養護費用下各規劃年度內養護費用分配比例較接近，均為第1年養護費用最大，占比達90%以上，其余4年內分配費用相當。這種養護費用分配趨勢與實際分配接近。養護費用上限值影響路面PCI值，上限費用越高，PCI值越大，上限費用為30 000元時第1年PCI值比上限費用為25 000元時第1年PCI值高6.5左右，且上限養護費用越低，規劃期內PCI值下降越明顯。3種養護費用下5年規劃期內PCI最小值分別為92、86、81，均滿足水平約束2的要求。

3 結論

(1) 可采用蟻群算法在確定路面養護費用上限值后對路面規劃期內養護費用進行最大效益化分配；若養護費用不明確，可采用蟻群算法基于PCI值等指標提供多個養護水平進行養護費用分配。

(2) 湛徐高速公路的養護費用較充足及一般的情況下，規劃期內第1年養護費用分配值均最大，超過總費用的90%，后期各年養護費用相當；規劃期總的養護費用水平越高，各年度PCI均值越高；上限養護費用越低，規劃期內PCI值下降越明顯。