感受坐標(biāo)思想 把握坐標(biāo)內(nèi)涵

孔凡哲

數(shù)軸是數(shù)形結(jié)合的典范.平面直角坐標(biāo)系由兩條原點重合且互相垂直的數(shù)軸組成，它的發(fā)明，使得代數(shù)式與圖形有機(jī)結(jié)合在一起，不僅可以使代數(shù)問題幾何化.而且可以使幾何問題代數(shù)化.

一維圖形就是一條直線.在直線上確定點的位置，必須確定一個基準(zhǔn)點和一個基準(zhǔn)方向，這個點就是原點，這個方向就是正方向，同時，還要確定度量單位，即單位長度，在確定了原點、正方向和單位長度的直線上，任何一個點都對應(yīng)著唯一的一個實數(shù)，而且僅僅需要一個實數(shù)就可以確定點的位置，故數(shù)軸上的點和實數(shù)是一一對應(yīng)的，而這個實數(shù)就是點的坐標(biāo).

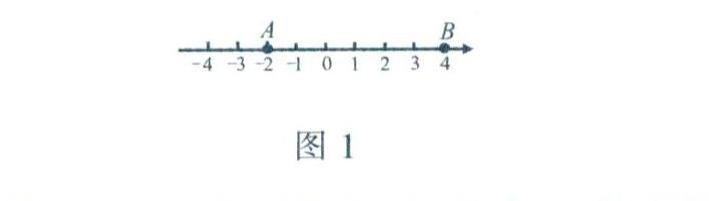
如圖1所示，數(shù)軸上點A的坐標(biāo)為-2.若已知某點的坐標(biāo)是4，則這個點在點B處，

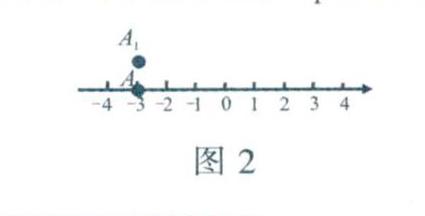
思考1：如圖2所示，如果點A的坐標(biāo)為-3，點A的正上方一個單位長度處有一個點A1，那么該如何表示點A.的位置？

點A1和點A的橫向上的位置都是-3，但是縱向上的位置是不同的，相差一個單位長度.利用定位一維圖形上的點的方法，無法定位點A1，必須增加新的量才能解決問題.

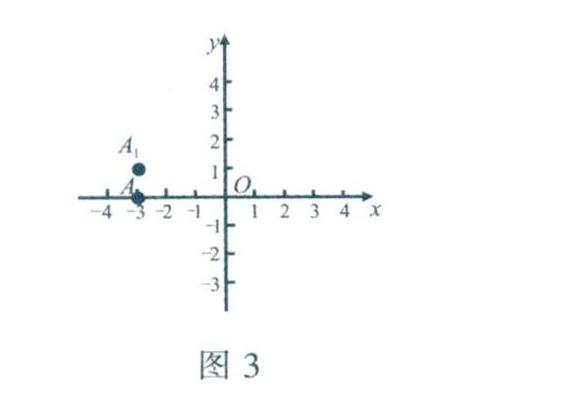
引入縱向軸線，在平面內(nèi)再畫一條與已知數(shù)軸垂直，且原點重合的數(shù)軸，組成平面直角坐標(biāo)系.水平的數(shù)軸稱為x軸或橫軸，習(xí)慣上取向右為正方向;豎直的數(shù)軸稱為y軸或縱軸，習(xí)慣上取向上為正方向;兩坐標(biāo)軸的交點為平面直角坐標(biāo)系的原點（如圖3所示）.

點A，的橫向上的位置會在x軸上體現(xiàn)，縱向上的位置會在y軸上體現(xiàn)，過點Ai分別向x軸、y軸作垂線，得到了與x軸、y軸相交的兩個點（垂足）以及兩個點分別對應(yīng)的實數(shù)，我們可以用這個實數(shù)對來表示點A，的位置.

因此，點A1的坐標(biāo)為（-3，1）.

在平面內(nèi)確定一個點的位置，只需要一個數(shù)對就可以了，這個數(shù)對叫作有序數(shù)對.之所以稱之為有序數(shù)對，是由于數(shù)對是一個整體，數(shù)對中的兩個數(shù)有順序之分，當(dāng)a≠b時，（a，b）所表示的點與（b，a）所表示的點的位置是不同的，

思考2：若再畫一條與已知數(shù)軸原點重合、但不垂直的數(shù)軸，能否表示點A1的位置？

答案是肯定的，這樣的坐標(biāo)系我們稱之為斜坐標(biāo)系.

當(dāng)把兩條數(shù)軸垂直放置時，更方便標(biāo)記點的位置，因此在實際問題中，我們常常建立適當(dāng)?shù)钠矫嬷苯亲鴺?biāo)系，根據(jù)點的位置寫出它的坐標(biāo)，

如圖4，建立平面直角坐標(biāo)系后，平面上的點可分成兩條坐標(biāo)軸上的點以及四個區(qū)域內(nèi)的點，這四個區(qū)域稱為象限，右上方的區(qū)域稱為第一象限，按照逆時針的方向，其他區(qū)域依次稱為第二、第三和第四象限，兩條坐標(biāo)軸上的點是不屬于任何一個象限的.就好比兩間房子之間的隔墻是不屬于任何一方的，

在平面直角坐標(biāo)系中，以坐標(biāo)軸x軸為對稱軸，對稱點的坐標(biāo)特點為“橫坐標(biāo)不變，縱坐標(biāo)互為相反數(shù)”;以坐標(biāo)軸y軸為對稱軸，對稱點的坐標(biāo)特點為“縱坐標(biāo)不變，橫坐標(biāo)互為相反數(shù)”.

思考3：若平面內(nèi)有一點P（a，b），則點P關(guān)于坐標(biāo)原點的對稱點P'的坐標(biāo)是________.

關(guān)于坐標(biāo)原點對稱可以分解為先關(guān)于x軸對稱，再關(guān)于y軸對稱（或先關(guān)于y軸對稱，再關(guān)于x軸對稱）.進(jìn)行兩次軸對稱變換后的點，與原來的點成中心對稱，對稱點的坐標(biāo)特點為“橫坐標(biāo)、縱坐標(biāo)均互為相反數(shù)”，相當(dāng)于橫、縱坐標(biāo)均乘一1.即點P，的坐標(biāo)為（-a，-b）.

在平面直角坐標(biāo)系中，將點向左（或向右）平移n個單位長度（n是正數(shù)），平移后的點的坐標(biāo)特點為“縱坐標(biāo)不變，橫坐標(biāo)減少（或增加）n個單位長度”;將點向上（或向下）平移n個單位長度（n是正數(shù)），平移后的點的坐標(biāo)特點為“橫坐標(biāo)不變，縱坐標(biāo)增加（或減少）n個單位長度”.

思考4：若平面內(nèi)的一點沿著某一方向（非坐標(biāo)軸方向）平移，則平移后的點的坐標(biāo)應(yīng)該如何表示？

沿著某一方向（非坐標(biāo)軸方向）平移，可以分解為先沿著x軸方向平移，再沿著y軸方向平移（或先沿著y軸方向平移，再沿著x軸方向平移），平移后的點的橫、縱坐標(biāo)都會發(fā)生相應(yīng)的變化.

練一練

1.（2019年杭州）在平面直角坐標(biāo)系中，若點A（m，2）與點B（3，n）關(guān)于y軸對稱，則（

）.

A.m=3，n=2

B.m=-3，n=2

C.m=2，n=3

D.m=-2，n=-3

2.（2019年安順）在平面直角坐標(biāo)系中，點P（-3，m2+1）關(guān)于原點的對稱點在（

）.

A.第一象限

B.第二象限

C.第三象限

D.第四象限

3.（2019年廣安）若點M（x-l，-3）在第四象限，則x的取值范圍是____，

參考答案：

1.B

2.D

3.x>1