基于蒙特卡洛方法的燃料組件壓緊力研究

(中國核動力研究設計院，四川 成都 610213)

燃料組件壓緊系統驗證中，需分析確定在正常運行期間壓緊組件能防止燃料組件跳起，以保證燃料組件的完整性。

目前，在核電工程上通常采用的壓緊力驗證分析方法為確定論分析方法，并采用最保守的假設，所有的設計參數均取對最小壓緊力最不利的極限值。造成計算得到的壓緊力與堆內的實際值差別很大。這種分析方法大大增加了燃料組件防跳起的安全性，但同時可能出現壓緊力裕量不足的情況。如果就此修改壓緊系統設計來增加壓緊力，使得驗證結果滿足要求；此時真實的壓緊力可能會過大，反而會造成燃料組件發生彎曲，從而可能延長控制棒的落棒時間，甚至出現不完全落棒，進而影響反應堆的安全運行[1]。因此，為優化壓緊系統的設計，在保證足夠壓緊力的同時減小對燃料組件彎曲的影響，需研究更為合理的壓緊力計算方法。

在保證壓緊的前提下減小施加到燃料組件上的軸向壓緊力成為壓緊系統設計新的關注重點，也對壓緊系統的壓緊力大小提出了更加苛刻的要求。壓緊系統設計時不能為了保證燃料組件的壓緊而僅從結構設計上增加壓緊力，也需要通過更為精確的壓緊力計算方法來增加壓緊力值。為了在保證壓緊系統壓緊功能的同時，燃料組件不致承受過大的軸向壓緊力，本文研究采用蒙特卡洛方法計算了燃料組件板彈簧壓緊力對燃料組件壓緊影響，并對蒙特卡洛方法的精準度進行了研究。

1 壓緊系統分析驗證方法

1.1 方法概要

燃料組件的壓緊狀態與反應堆及燃料組件自身的眾多參數相關，無論采用哪一種方法進行壓緊力的計算和驗證，都需要考慮這些因素影響，將相關參數作為計算輸入。根據不同參數的特性，可將輸入參數劃分為可變參數和固定參數兩大類。

對于給定的燃料組件、壓緊系統和堆芯，固定參數的取值不會隨計算方法發生變化。其取值的確定也會考慮相應的保守性，如壓緊板彈簧剛度特性采用根據實驗數據擬合得到的下限值(最小剛度)。

對于可變參數，數據組成包括名義值及其不確定度，不同的計算方法差異在于對于參數不確定的處理，對于整個計算所考慮的物理模型相同。可變參數包括堆腔高度、組件軸向結構參數、壓緊系統結構參數及輻照特性等。

1.2 確定論方法

目前工程設計中一般采用保守假設的確定論方法(Deterministic Methodology)進行壓緊系統驗證。通過對可變參數的名義值加上或者減去不確定度以使平衡力達到最小，從而使計算結果達到最保守的程度，以包絡實際反應堆中所有燃料組件的最危險壓緊狀態[2]。

采用確定論方法計算壓緊力時，對各種影響平衡力的參數均取了極限值。但實際運行中，各種影響平衡力的參數均同時處于極限值的概率是非常小的。因此，采用確定論方法驗證計算得到的最小平衡力過于保守[3]。

1.3 蒙特卡洛方法

蒙特卡洛方法(Monte Carlo Algorithm)也稱統計模擬方法，是一種以概率統計理論為指導的一類非常重要的數值計算方法，可以使用隨機數(或常見的偽隨機數)來解決很多計算問題。

采用蒙特卡洛方法計算時，使用數學模擬的方法，進行大量模擬實際情況的計算。每次計算時，可變參數按照一定的概率分布規律隨機生成數據，并經模型計算得到相應的輸出結果。最終對大量的計算結果進行統計處理，得到在一定置信度下壓緊力和平衡力的統計輸出結果[4]。為了保證蒙卡方法計算壓緊力的可靠性及適用性，需選擇適宜的輸入參數分布類型及數據統計時的置信度。

2 壓緊驗證結果對比

采用蒙特卡洛方法驗證燃料組件的壓緊，需要開發配套的軟件，目前中國核動力研究設計院自主研發的HOFA軟件可以實現該功能[5]。經分別采用確定論方法及蒙特卡洛方法對燃料組件進行壓緊力驗證，壓緊力及平衡力計算結果對比見表1，其中蒙特卡洛方法中的置信度為95%。

通過對采用確定論方法及蒙特卡洛方法計算的最小壓緊力、平衡力數據進行對比，可以看出在未考慮最小設計裕量時，采用確定論方法計算的平衡力已經不足，不滿足設計準則。采用蒙特卡洛方法計算的壓緊力及平衡力都能獲得較大的提升。相較于確定論方法，采用蒙特卡洛方法最少獲取755 N的提升，在壓緊情況最惡劣的熱態邊緣區仍有707 N的裕量，滿足了設計準則要求的最小250 N的裕量，從而避免由于計算方法的過度保守性導致壓緊力不足的問題。

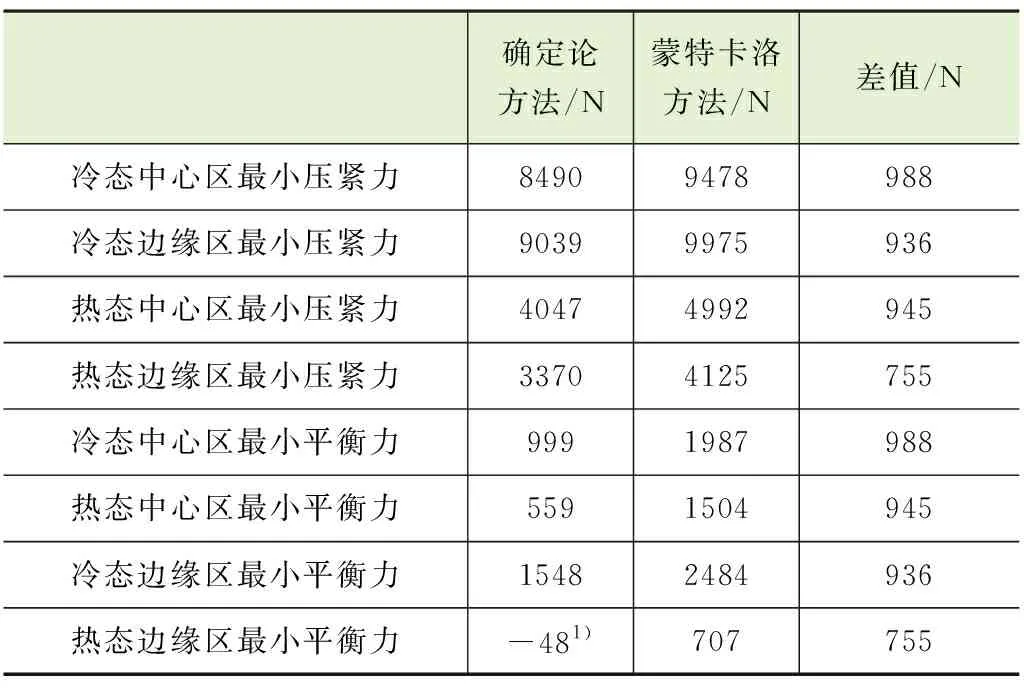
表1 最小力計算結果對比

3 壓緊力離散度對比分析

早期的燃料組件設計中，板狀壓緊彈簧設計中重點關注了壓緊系統的壓緊功能以保證燃料組件運行過程中不發生跳起，未考慮過大壓緊力對燃料組件彎曲的影響。

采用確定論方法計算的壓緊力為最極限的值，離散度大，偏離燃料組件堆內所受的實際壓緊力較大。以前在壓緊系統設計時，如果最小壓緊力不能滿足壓緊的要求，設計者往往會修改結構設計來增加壓緊力。如果分析方法得到的結果不夠精確，燃料組件在堆內承受的實際壓緊力會比計算得到的最小壓緊力大得多，可能會對燃料組件產生不利的影響。壓緊系統設計不能繼續按照保守壓緊力的方式進行設計，需要更為準確的壓緊力分析方法來計算壓緊力值，以避免過大壓緊力對組件的不利影響。通過研究壓緊力的離散度，來分析燃料組件壓緊力評價方法的準確性。

3.1 離散度評價指標

離散度是指變量各個取值之間的差異程度，可采用極差進行衡量。極差,是觀測變量的最大取值與最小取值之間的離差，也就是觀測變量的最大觀測值Max(xi)與最小觀測值Min(xi)之間的區間跨度，采用下式進行計算：

R=Max(xi)-Min(xi)

為評價壓緊力分析結果的離散度，采用極差進行各方法計算結果的離散度分析。

3.2 離散度對比

從方法原理上講，在計算壓緊力時，確定論方法中對可變參數取極限值，因此壓緊力的最小值和最大值均比蒙特卡洛方法計算結果更保守。確定論方法計算的壓緊力變化范圍很大，離散度高。采用蒙特卡洛方法計算的壓緊力變化范圍較小，數據更精確，離散度低。

采用確定論方法及蒙特卡洛方法對燃料組件進行壓緊力計算。對不同計算方法下各工況壓緊力的離散度進行了研究分析，研究對象為壽期內各時間點對應工況下壓緊力的極差。

蒙特卡洛方法計算的壓緊力被包絡在確定論方法的最小值和最大值之間，與根據方法原理判斷的預期是相符的。蒙特卡洛方法計算的壓緊力的冷態及熱態下極差變化相對確定論方法減小45%～65%，見圖1、圖2。以上對比數據表明采用蒙特卡洛方法可有效降低壓緊力計算結果的離散度，提高計算結果的準確性。

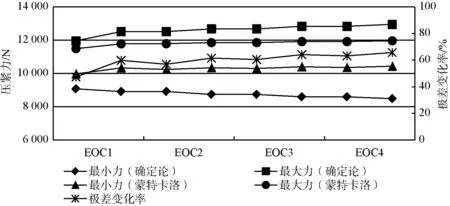
圖1 冷態壓緊力分布及極差變化率Fig.1 Distribution of hold-down force andchange of range in cold state

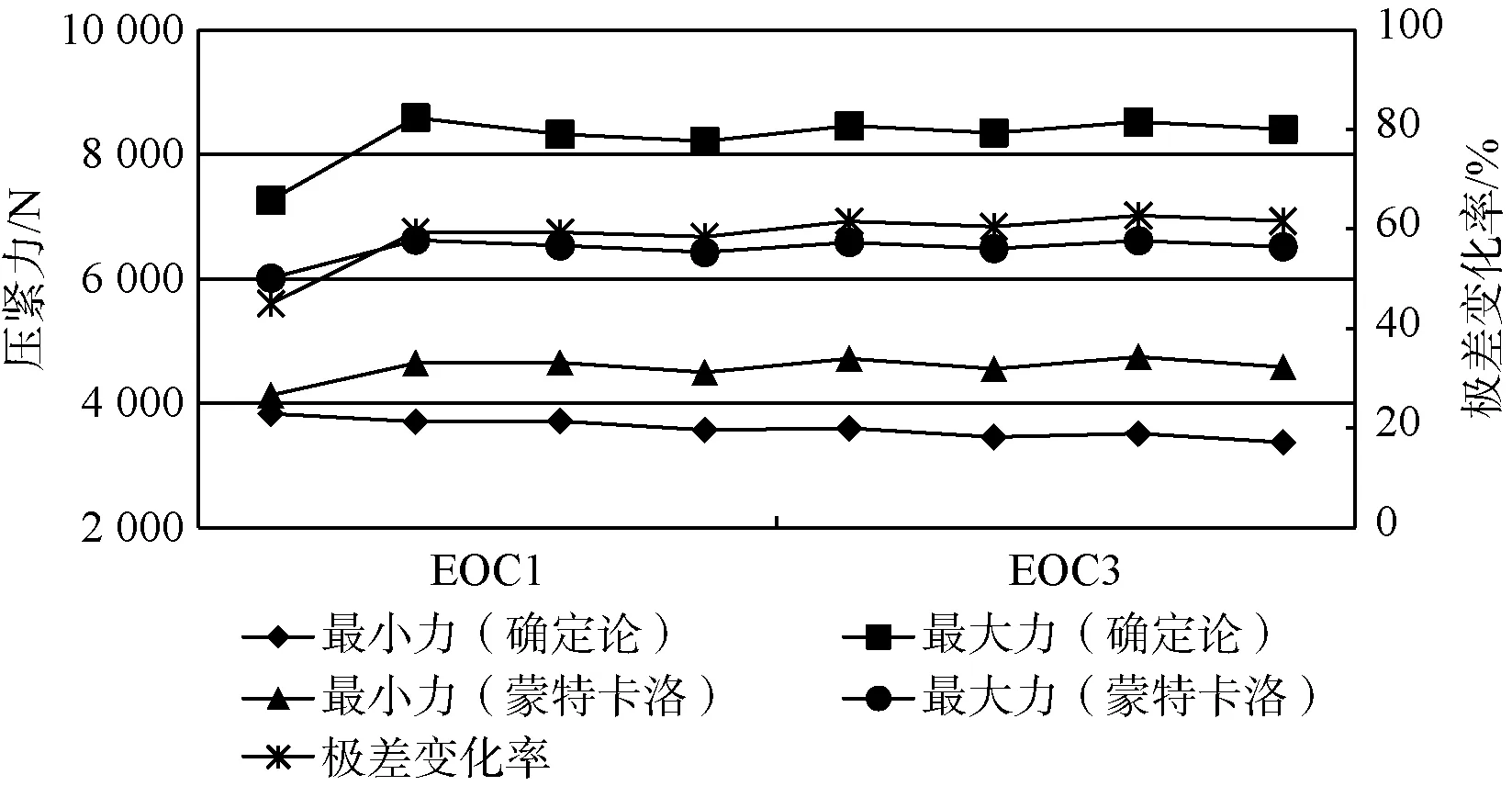
圖2 熱態壓緊力分布及極差變化率Fig.2 Distribution of hold-down forceand change of range in hot state

4 結 論

采用確定論方法計算得到的燃料組件壓緊力不夠精確，過于保守。在堆內燃耗水平不斷提高的情況下，采用確定論方法對燃料組件進行驗證時，可能會出現壓緊力不滿足準則要求的情況。本文基于蒙特卡洛方法對燃料組件壓緊力進行了分析，結論如下：

1)采用蒙特卡洛方法計算能夠獲取更大的壓緊力裕量，可避免在實際工程中由于計算方法的過度保守性導致壓緊力不足的問題，從而保證燃料組件設計滿足工程驗證的要求。

2)采用蒙特卡洛方法替代確定論方法進行燃料組件壓緊力分析驗證，降低了壓緊力分析結果的離散度，提高了壓緊力計算的準確性，能夠為設計者設計壓緊系統時避免燃料組件承受過大的壓緊力提供指導。