頻域濾波產生的時域端點效應及避免方法

王 顏

1 頻域濾波產生的時域端點效應

濾波是數字信號處理中的常見過程。通過選頻濾波可以提取時域信號有用的頻率分量，壓制干擾信號。選頻濾波通常在頻域進行，其具體步驟是：

（1）對長度為N 的時域信號x（n）作離散傅里葉變換（DFT），得到對應的頻域信號X（k）。通常使用快速傅里葉變換算法（FFT）進行。

（2）將頻域信號X（k）各點處的值與頻域濾波器F（k）相同頻率處的值相乘，得到濾波后的頻域信號Y（k）：

（3）對 Y（k）做離散傅里葉反變換（IDFT），即得到頻域濾波后的時域信號 y（n）。通常使用快速傅里葉反變換算法（IFFT）進行。

對時域信號進行頻域濾波后所得到的信號可能在時域的一端被截斷，被截去的部分在另一端出現，造成時域信號失真。本文稱這種時域信號截斷和移位造成的信號失真為頻域濾波的時域端點效應。下文通過編寫MATLAB 程序，應用式（2）所表示的帶余弦鑲邊的帶通濾波器對地震勘探數據處理中廣泛應用的雷克子波[1]進行頻域濾波，說明頻域濾波的流程，并指出這一過程產生的時域截斷和移位現象，即頻域濾波的時域端點效應。

式（2）中，l1和h1分別是低頻端和高頻端的截止頻率，l1-l2和h1-h2分別是低頻端和高頻端的過渡帶，在過渡帶內濾波器的幅值以余弦函數的形式從1 衰減到0. 顯然，對于連續的頻率，該濾波器的頻譜是光滑的。

現將濾波器低頻端和高頻端的截止頻率分別設為20Hz，60Hz，過渡帶寬度設為 3Hz，即 l2=16，l1=20，h1=60，h2=64，則濾波器的頻譜如圖1 所示。

圖2 和圖 3 分別是主頻 40Hz 的雷克子波信號及其頻譜。

圖2 40Hz 的雷克子波信號

圖4 和圖5 分別是應用圖1 所示濾波器進行步驟（2）所述濾波后的信號的頻譜和經過離散傅里葉反變換后所得的時域信號。

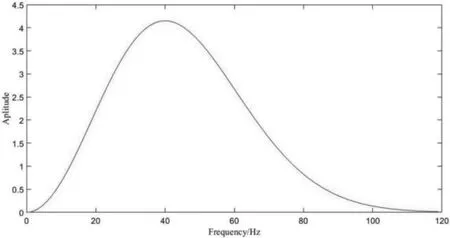
圖3 40Hz 對應的頻譜

圖4 濾波后的信號的頻譜

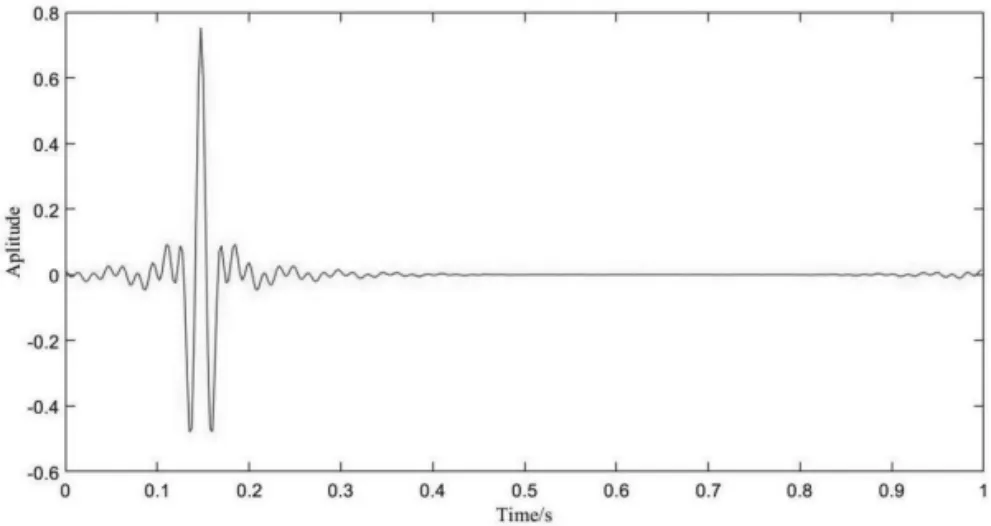
圖5 經過離散傅里葉反變換后所得的時域信號

從圖5 可以看出，濾波后的信號在t=0 處被截斷，被截去的部分出現在了時間軸的末端，即出現了前文所述的端點效應。

2 端點效應產生的原因分析

根據離散傅里葉變換和反變換的性質[2]，對頻域信號進行點數為N 的等間隔采樣，其離散傅里葉反變換對應的時域信號為

由（3）式可知，如果原來的時域信號x（n）經過頻域濾波后對應的延伸至a ≤n ＜0 范圍內，則這段信號會被截除，同時因為被截除的信號會出現在時間軸末端的a+N ≤n ≤N-1 位置。類似的，如果延伸至N ≤n ≤b 范圍內，這段信號同樣會被截除，并出現在0≤n ≤b-N 位置。

3 頻域濾波中避免時域端點效應的原理

本文現從時域和頻域運算間的關系角度分析為避免時域端點效應，頻域濾波過程應滿足的條件。

由傅里葉變換的性質可知，頻域的乘積運算等價于時域的卷積運算，所以。

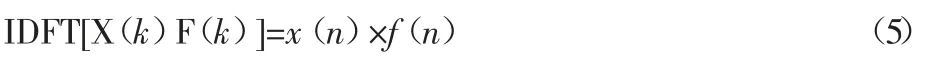
由上式可知經過頻域濾波后的信號相當于原信號在時域與濾波器的時域響應做卷積運算的結果。假設x（n）和 f（n）在時間軸上的第一個和最后一個非零值出現的位置分別為 N1、N2和 N3、N4，濾波后的信號為 xf（n），則：

若xf（x）≠0，則x（m）≠0 且f（n-m）≠0，所以m ≤N2，nm ≤ N4，兩式相加得。

由（7）式可知，原信號的采樣總時長N 滿足（8）式時，可以確保濾波后的信號在時間軸末端不被截斷。

（8）式可以變形為

因為對于傅里葉反變換，時間軸的兩個方向是等價的，所以由（9）可以得到確保濾波后的信號在時間軸起始端不被截斷的條件。

（9）式和（11）式指出了原信號和濾波器的參數滿足什么條件時，可以保證經過頻域濾波的信號在時域不出現端點效應。從推導過程可以看出，這兩個不等式表達的是避免時域端點效應的充分條件，而非必要條件。所以若頻域濾波過程中出現了時域端點效應，可以按滿足（8）（11）兩式的方向調整相關參數，但相關參數并非必須滿足兩式才能避免端點效應。

4 避免時域端點效應的方法及實驗驗證

本節介紹了避免頻域濾波的時域端點效應的兩種具體的方法，并以濾波后的信號在時間軸起始端被截斷造成的端點效應為例，通過MATLAB 程序進行了實驗驗證。

4.1 時域補零

通過在原信號的末端增加M 個零值點，可使式（8）中的N增大M 而N2、N4不變，各參數整體向滿足該不等式變化，因此當M 大于某個值時，信號在時間軸末端被截斷造成的端點效應會得到避免。

類似的，通過在原信號的起始端增加M 個零值點，可使式（11）中的N、N1各增大M。因為頻域采樣點數增加了M，所以濾波器的離散傅里葉反變換時長增加了M，由離散傅里葉反變換結果的對稱性可知，N3增大了M/2。因此（11）式左端增大了M，右端增大了3M/2，各參數整體向滿足該不等式變化，因此當M大于某個值時，信號在時間軸起始端被截斷造成的端點效應會得到避免。

在圖2 所示信號起始端增加100 個零值點，得到圖6 所示延時0.25s 后的信號。

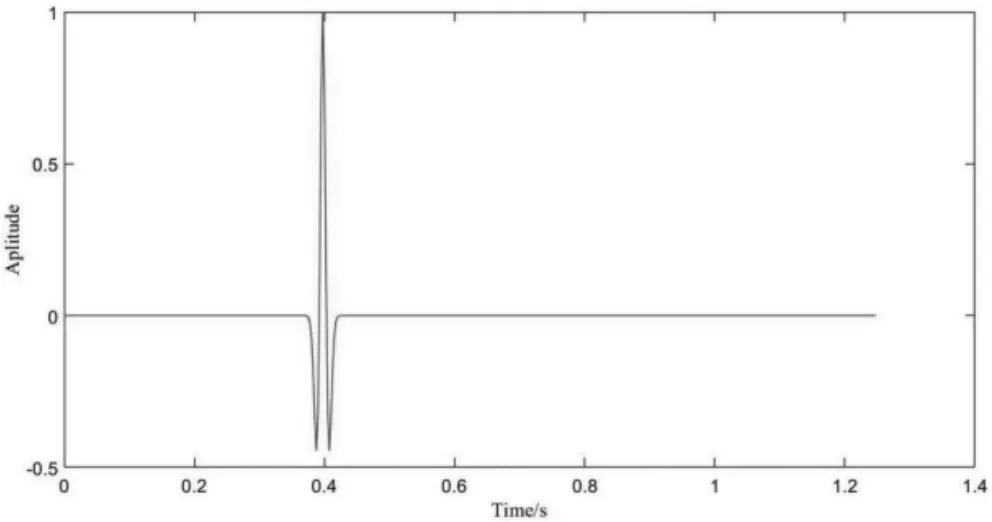
圖6 延時0.25s 后的信號

根據離散傅里葉變換的性質，信號的頻譜（振幅譜）不發生變化，且仍為均勻采樣，但采樣數比原來增加100，采樣間隔變小。因此要通過頻域濾波獲取與第一節中相同的頻率成分，所使用的濾波器應滿足連續頻譜與第一節實驗中的濾波器相同，但采樣位置與圖6 信號頻譜的采樣位置相同。該濾波器的頻譜如圖 7 所示。

圖7 與圖6 信號頻譜的采樣位置相同下的濾波器頻譜

圖8 紅線和藍線分別是第一節的實驗和本實驗所用濾波器的時域響應，可以看出藍線第一個非零值的位置比紅線增大了50，與理論分析相符。

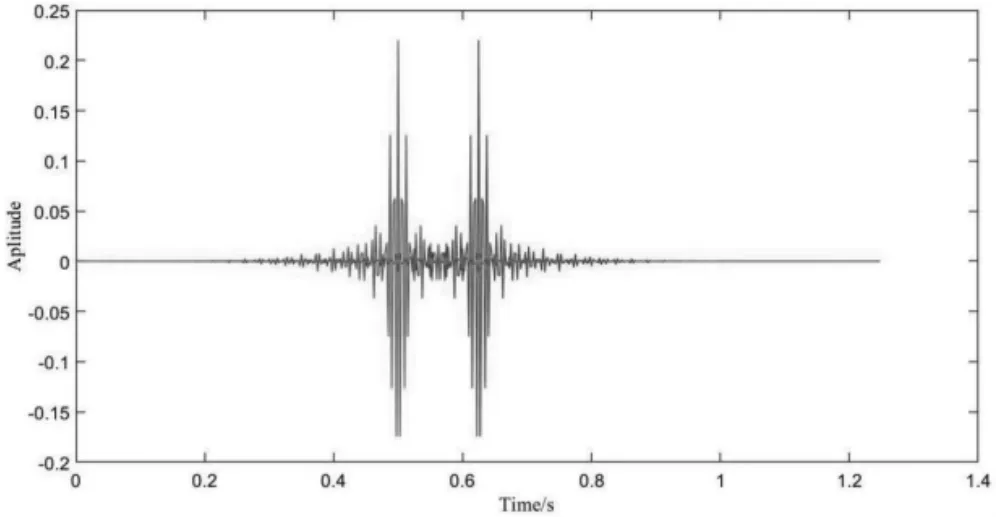
圖8 不同實驗所用濾波器的時域響應

圖9 是經過頻域濾波得到的時域信號，可見圖5 中的端點效應消失，證明了時域補零方法的有效性。

圖9 經過頻域濾波得到的時域信號

4.2 拓寬濾波器頻譜

通過拓寬濾波器頻譜，使其時域響應變窄，（8）式中的N4變小，（11）式中的N3 變大，兩式中的參數都向使不等式成立的方向變化。因此信號在時間軸起始端和末端被截斷造成的端點效應都可以通過拓寬濾波器頻譜來解決。

將第一節實驗所用濾波器的過渡帶寬度增加到9Hz，其頻譜如圖10 所示。

圖1 0 濾波器過渡帶寬度增加到9Hz 時的頻譜

圖11 紅線和藍線分別是第一節的實驗和本實驗所用濾波器的時域響應，可以看出本實驗濾波器的時域響應變窄，第一個零值點位置后移，最后一個零值點位置前移。

圖12 是用過渡帶寬度增加的濾波器對圖2 所示信號進行頻域濾波的結果，可見圖5 中的端點效應消失，證明了拓寬濾波器頻譜方法的有效性。同時因為濾波器的過渡帶變得更加平緩，吉布斯效應也得以減弱。

圖11 不同實驗所用濾波器的時域響應

圖12 經過頻域濾波得到的時域信號

5 結論

對數字信號進行頻域濾波所得到的時域信號可能在一端被截斷，被截去的部分出現在另一端，造成時域信號失真。本文稱這一現象為頻域濾波的時域端點效應。通過理論分析和數值實驗，得出以下結論：

（1）頻域濾波的時域端點效應產生的原因是原信號經過頻域濾波后時寬變長，因采樣總時長有限而在一端或兩端被截斷。同時因為頻域信號對應的時域信號的周期性，在一端被截除的信號在另一端重現。

（2）假設原信號采樣總時長為N，原信號和濾波器的時域響應在時間軸上的第一個和最后一個非零值出現的位置分別為 N1、N2和 N3、N4，則上述參數滿足 N-1≤N1+N3可以確保不出現信號在起始端被截斷造成的端點效應；滿足N-1≥N2+N4可以確保不出現信號在末端被截斷造成的端點效應。

（3）若頻域濾波過程中出現了時域端點效應，可以按滿足結論（2）中的兩個不等式的方向調整相關參數。但因為這兩個不等式表達的是避免時域端點效應的充分條件而非必要條件，所以調整后參數并非必須滿足兩式。

（4）通過在原信號的起始端補零，可以避免濾波后的信號在起始端被截斷造成的端點效應；在原信號的末端補零，可以避免濾波后的信號在末端被截斷造成的端點效應。

（5）通過拓寬濾波器頻譜，信號在時間軸起始端和末端被截斷造成的端點效應都可以得到解決。