云輔助移動邊緣計算中的計算卸載策略

王 妍,葛海波,馮安琪

(西安郵電大學 電子工程學院,西安 710121)

0 概述

隨著移動設備的普及,計算密集型、時延敏感型等新興移動應用不斷涌現并迅速受到用戶的青睞,如增強現實、圖像識別、網絡游戲、車聯網等[1]。這類新興的應用通常需要消耗大量的計算資源,以滿足低時延需求。然而,資源有限的移動設備很難滿足上述移動應用的需求[2]。計算卸載是一種有效的解決方案,通過卸載計算任務到云服務器或者邊緣服務器,從而達到緩解計算和存儲的限制、降低時延的目的。移動云計算(Mobile Cloud Computing,MCC)被認為是一種很有效的卸載計算任務的方法,其強大的計算能力可以顯著降低移動服務的處理時延。然而,將計算任務卸載到空間上遠離移動設備的云服務器上會造成較高的傳輸時延,增加能量消耗。為了解決云計算卸載過程中面臨的高傳輸時延等問題,移動邊緣計算(Mobile Edge Computing,MEC)應運而生[3],MEC的核心思想是將服務器的計算和存儲資源遷移到移動設備附近,降低移動服務處理過程中的傳輸時延、處理時延,減少能量消耗。移動邊緣計算是移動云計算的一種特殊情況。

在計算卸載問題中,MCC和MEC各有利弊,適用于不同的移動服務[4]。當面臨延遲敏感任務時,MEC以其靠近移動設備、傳輸延遲短的優點,可以提供比MCC更好的服務,當處理非延遲敏感任務時,則會突出MCC中計算資源豐富的優勢。因此,MCC和MEC兩者應相互協調、相互補充,確保計算卸載策略能滿足不同的應用場景。

本文綜合考慮MCC計算資源豐富以及MEC靠近移動設備的優勢,提出一種云輔助移動邊緣計算的計算卸載策略(CAME),在此基礎上,設計基于改進遺傳算法的計算卸載算法(CAMEGA),優化移動服務的運行時間和設備能耗,從而得到系統總代價較優的計算卸載策略。

1 相關研究

計算卸載是研究MEC的關鍵問題之一。近年來,研究人員對MEC中的計算卸載問題進行了大量研究,并且取得了突破性的進展。這些研究旨在探索制定最佳卸載決策,達到降低時延和節省移動設備能耗的目的。文獻[5]利用馬爾科夫鏈理論分析給定計算任務的時延,運用一維搜索算法尋找時延最小的計算卸載策略。文獻[6]研究在移動邊緣計算環境下,卸載延時和可靠性之間的權衡問題,利用基于啟發式搜索、重構造線性化技術和半定松弛3種算法,實現系統延時和卸載失敗率最小。文獻[7]運用排隊網絡的方法分析系統時延,提出一種具有線性復雜度的算法,該算法能顯著降低系統時延。文獻[8]提出一種基于李亞普諾夫的動態卸載算法,在滿足指定應用程序對時延要求的前提下,實現系統節能。文獻[9]研究一個帶有能量收集器件的MEC系統,提出基于李亞普諾夫優化的動態計算卸載算法,實現應用程序的執行延遲最小。文獻[10]提出一種細粒度卸載策略,將任務卸載問題表示為一個有約束的0-1規劃問題,采用BPSO算法,旨在滿足嚴格的延時約束的同時,最大限度地減少能量消耗。文獻[11]研究了由多個用戶組成的移動邊緣計算卸載系統中的資源分配問題,將最優資源分配問題表示為一個凸優化問題,實現在滿足時延要求的條件下,移動設備能耗最小。文獻[12]提出一種面向優先級業務的邊緣計算資源分配方法,根據業務價值賦予相應的優先級,對不同優先級的任務進行加權資源分配,旨在降低業務的執行時間和能耗。文獻[13]提出基于拉格朗日的計算卸載策略,將移動邊緣計算框架下的計算卸載問題建模為一個凸優化問題,采用拉格朗日乘子法優化移動終端總的計算時間和能耗。文獻[14]采用云輔助移動邊緣計算框架,旨在以最小的系統成本保證用戶服務質量。文獻[15]提出一種新的異構網絡兩層計算卸載框架。基于此框架,設計有效的計算卸載方案,以使總體能耗最小化。文獻[16]提出一個云、MEC和LoT集成的融合框架,解決MEC面臨的可擴展問題,設計了一個選擇卸載方案,在滿足時延要求的條件下實現移動設備能耗最小。文獻[17]提出一種資源優化方法來最小化多天線接入點的能耗。文獻研究總結如表1所示,其中,√為是,×為否。

表1 不同方案的計算卸載策略

上述對于移動邊緣計算環境下的計算卸載問題的研究工作,大部分只是將能耗或時延其中一項作為優化目標,或者沒有考慮任務之間的數據依賴關系和順序依賴關系。此外,大部分研究集中于應用MEC或MCC來卸載計算任務,并未考慮兩者之間的協作。很少有文獻在綜合考慮以上3種情況的基礎上研究計算卸載問題,這就導致設計的卸載策略局限性較大。因此,設計一個適用于不同移動服務的計算卸載策略成為計算卸載問題中的難點。為了解決上述問題,本文提出CAMEGA計算卸載算法。主要工作如下:

1)綜合考慮MEC傳輸時延低、計算能力有限而MCC傳輸時延高、計算資源豐富的特點,提出云輔助移動邊緣計算的計算卸載框架(CAME)。

2)考慮到任務之間的依賴關系,將復雜的移動服務簡化為具有優先約束關系的工作流模型處理。

3)設計基于改進遺傳算法的計算卸載算法(CAEMGA),利用改進遺傳算法循環得到最優卸載策略,最小化移動服務總的執行時間和能耗。

2 系統模型

本節主要闡述系統模型,系統模型主要包括移動服務模型和計算卸載模型。

2.1 移動服務模型

本文主要研究云輔助移動邊緣計算環境下單用戶單個移動服務的計算卸載問題。將復雜的移動服務簡化為具有優先約束關系的工作流模型處理。用S={s1,s2,…,si,…,sn}表示工作流中任務的集合,n為任務的數量,用戶可以通過調整任務的數量以及任務間的依賴關系來模擬各種各樣的移動服務。每個任務被建模為一個二元組{αi,βi},其中,αi為第i個任務的工作量,βi為輸出數據量。

在移動服務的運行過程中,本地設備輸入數據,第一個任務從本地設備獲取數據,因此第一個任務必須在本地設備中執行。類似地,當移動服務運行完后,應該把輸出數據傳回本地設備,最后一個任務也必須在本地執行。

2.2 計算卸載模型

計算卸載模型如圖1所示,移動設備通過移動網絡連接到基站。當移動設備運行移動服務時,可以將工作流中的任務卸載到邊緣服務器或云服務器中執行。邊緣服務器和云服務器接收來自移動用戶的請求并處理,最后將處理結果返回給移動用戶。移動用戶可以根據移動服務的需求選擇任務部分卸載或者完全卸載。由圖1可知,用戶U3將工作流中第2個任務卸載至邊緣服務器中執行,將第3個任務卸載至云服務器中執行,第1個和第4個任務在本地設備執行。

圖1 計算卸載模型Fig.1 Computation offloading model

邊緣服務器可通過一個二元組E={Ce,Fe},其中,Ce為邊緣服務器處理1 bit數據所需的CPU周期數,Fe為邊緣服務器計算能力。

云服務器可通過一個二元組E={Cc,Fc},其中用Cc表示云服務器處理1bit數據所需的CPU周期數,Fc為云服務器計算能力。

3 問題分析

圖2展示了一個由9個任務組成的移動服務工作流,這9個任務的執行順序具有優先約束關系,箭頭表示任務執行的先后順序,這些任務可以在本地設備、邊緣服務器或云服務器中執行。由圖2可以看出,任務S1、S2、S5、S9在本地執行,S3、S4、S7在邊緣服務器中執行,S6、S8在云服務器中執行。

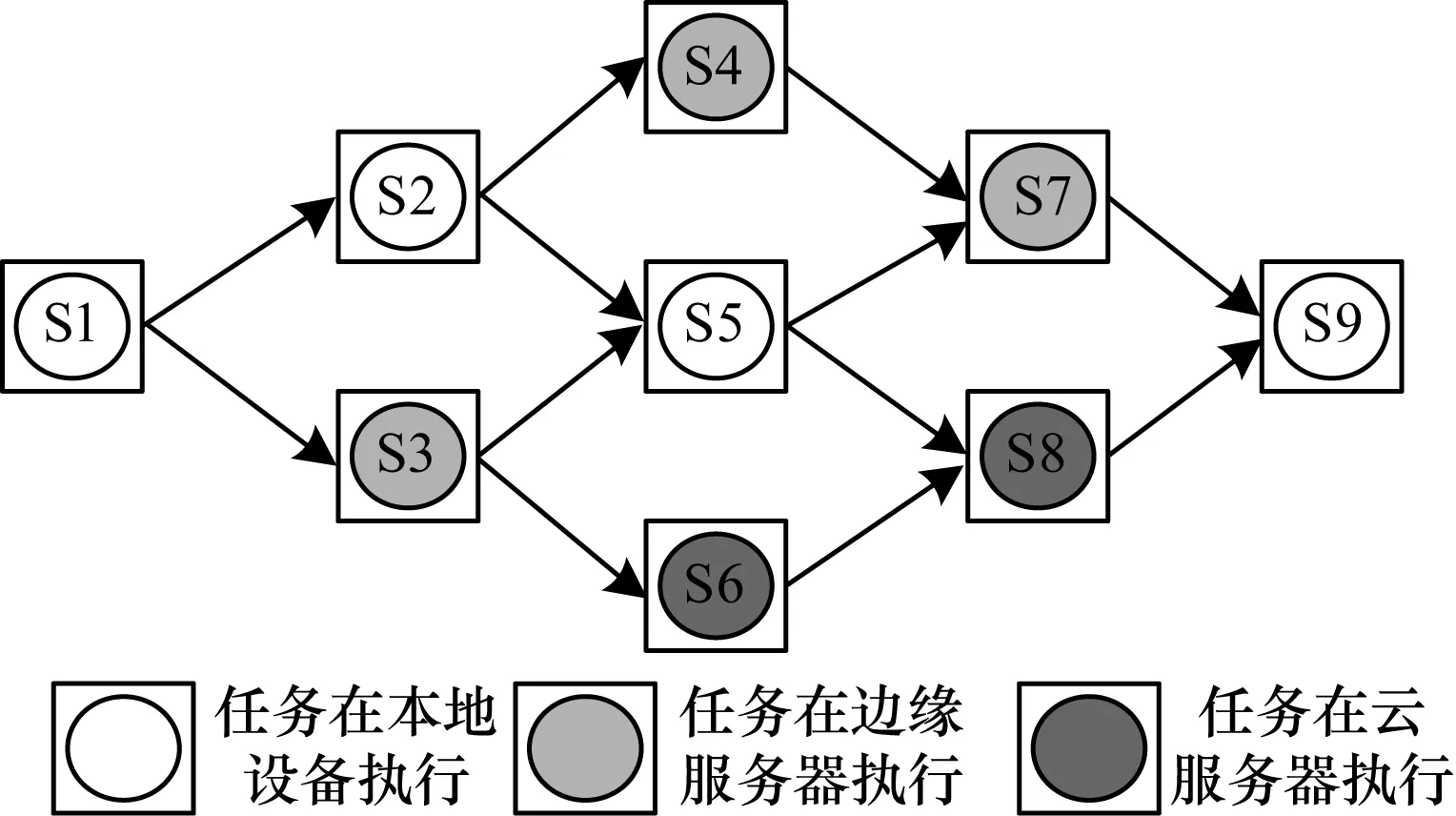
圖2 任務卸載模型Fig.2 Task offloading model

本文旨在制定最佳的卸載策略,實現工作流的執行時間和移動設備的能耗最小。因此,將目標函數定義為工作流執行時間和能耗的加權和。

F=ωT+(1-ω)E

(1)

其中,E為執行工作流服務過程中移動設備的總能耗,T為工作流執行的總時間,ω為時延權重系數,1-ω為能耗權重系數。ω可根據移動服務的需求及移動設備的狀態來設置,例如,當運行延時敏感型移動服務時,可以適當增加ω的值,當移動設備電量不足時,ω必須設置為較小的值。本文以時延敏感型移動服務為例,ω取0.8。

按照如下方式計算目標函數中的分量:

1)任務i在本地執行的計算時間為:

(2)

任務i在本地執行的能耗為:

El=Tl×Pl

(3)

2)任務i從本地卸載至邊緣服務器的總時間為:

(4)

任務i從本地卸載至邊緣服務器的總能耗為:

(5)

3)任務i從本地設備卸載至云服務器的總時間為:

(6)

任務i從本地設備卸載至云服務器的總能耗為:

(7)

綜上所述,移動服務運行的總時間和移動設備的總能耗可以表述為:

(8)

(9)

4 卸載算法設計

目前,研究人員使用智能算法解決優化問題[18-19]。本文選擇遺傳算法作為基礎算法,部分修改傳統遺傳算法,以滿足計算卸載問題的特殊需求[20-21]。

在云輔助移動邊緣計算的計算卸載系統中,移動服務工作流中的每個任務可在不同服務器上執行(本地、邊緣、云),這些服務器具有不同的計算能力,所以不同的執行位置會造成不同的執行時間和設備能耗。此外,當工作流中包含大量任務數時,會出現多個任務同時競爭一個計算資源的情況。因此,本文采用排序任務的執行順序來解決這個問題。考慮以上兩點,本文主要關注任務的執行位置和執行順序兩組變量,這兩組變量相互影響,共同決定卸載策略。如果分開優化每組變量,將不能得到最優卸載策略。本文采用改進遺傳算法,即嵌套遺傳算法,同時優化任務執行順序和執行位置。

4.1 編碼

本文采用改進浮點數編碼的編碼方式。與傳統的浮點數編碼不同的是,分別讓浮點數整數和小數部分映射不同的個體特征,即一種基因型映射兩種表現型,這樣編碼能夠降低算法復雜度,提高運算效率。假設n為任務總數,用集合X.Y={x1.y1,x2.y2,…,xi.yi,…,xn.yn}表示任務執行順序和執行位置,其中整數部分xi表示工作流中的某個任務,小數部分yi表示任務xi∈{s0,s1,s2,…,si,…,sn-1}的執行位置,yi=0表示任務在本地設備執行,yi=1表示任務在邊緣服務器執行,yi=2表示任務在云服務器執行。圖3描述的是編碼方案示例。

圖3 編碼方案示例Fig.3 Example of encoding scheme

4.2 適應度函數

在遺傳算法中,適應度是描述個體性能的主要指標,適應度越大,個體越優秀。根據適應度的大小,對個體進行優勝劣汰。本文關注的問題是搜尋最優卸載策略,實現移動服務工作流的執行時間與能耗的加權和最小化。因此,使用目標函數的倒數計算工作流的適應度值。

4.3 初始化

由于任務之間有一定的順序關系,因此借助優先約束矩陣PCM來初始化任務的執行順序。PCM是一個n×n矩陣,用D表示,Dij表示工作流中第i個任務與第j個任務的約束關系。當Dij=0時表示任務i和任務j沒有優先約束關系,可以同時執行;Dij=1表示任務i必須先執行;Dij=-1表示任務j必須先執行。可以根據任務的數量及任務之間的具體依賴關系自定義PCM矩陣,圖4為圖2中9個任務的優先約束矩陣。

圖4 優先約束矩陣

具體的操作步驟為:每次選取沒有先序任務或先序任務已經排序完畢的任務,即選取優先約束矩陣中所有Cij不等于-1的行數,然后把優先約束矩陣中與所選取任務相關的行和列都置為0,即選取任務Si后,將Cij、Cji都置為0。按照此方法繼續選取下一任務,直到形成一組可行任務序列。循環N次形成初始種群,N為種群規模。

完成任務執行順序初始化后,進行任務執行位置初始化。隨機產生0.0、0.1、0.2中的一個數,如果產生為0.0,則表示任務在本地設備執行,同理,產生0.1、0.2分別表示在邊緣服務器或云服務器中執行。

4.4 交叉

采用傳統的單點交叉法,進行任務執行位置的交叉操作,經過交叉操作后,得到新的個體X1.Y12和X2.Y21。

算法1排序交叉算法

輸入完成位置交叉操作的任務序列

輸出完成整體交叉操作的任務序列

Begin

1.生成[1,n]之間的隨機數r;

3.X12.Y12=X21.Y211≠φ

4.for i=1 to r

6.end for

8.for i=1 to r

10.end for

12.for i=1 to n+r

13.for m=1 to n

16.else

18.end if

19.end for

20.for i=1 to n+r

21.for m=1 to n

24.else

26.end if

27.end for

任務執行順序變異過程如圖5所示。

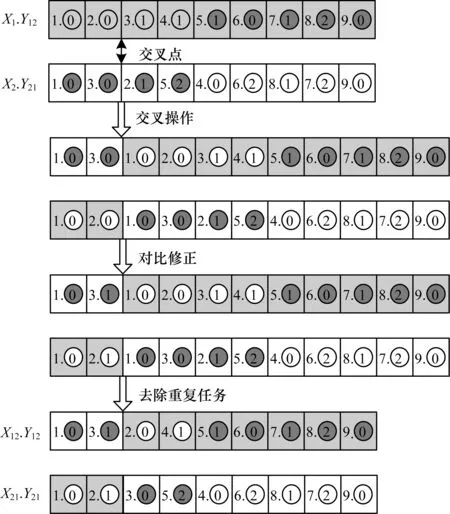
圖5 任務執行順序變異過程1Fig.5 Mutation process 1 of task execution sequence

4.5 變異

變異操作是將染色體中的某個基因值做出變動。隨機選取任務序列中一個任務作為變異點,以突變概率決定是否進行變異,若變異,則任務執行位置變為除當前執行位置之外的任一位置,即基因小數部分0變為1或2、1變為0或2、2變為0或1。

在執行任務執行順序的變異操作時,同樣需要考慮任務之間的優先約束關系。從任務集合X.Y中隨機選取一個任務xi.yi作為變異點,在任務集合X.Y中,以xi.yi為中心,分別往正反方向查找,直到找到xi.yi所有的先序任務集合{x1.y1,x2.y2,…,xa.ya}和后繼任務集合{xb.yb,xb+1.yb+1,…,xn.yn}。最后,在不包含xi.yi的先序任務和后繼任務的序列{xa+1.ya+1,xa+2.ya+2,…,xb+1.yb+1}中,隨機選取一個任務,與xi.yi交換執行順序。任務執行順序的變異過程如圖6所示。

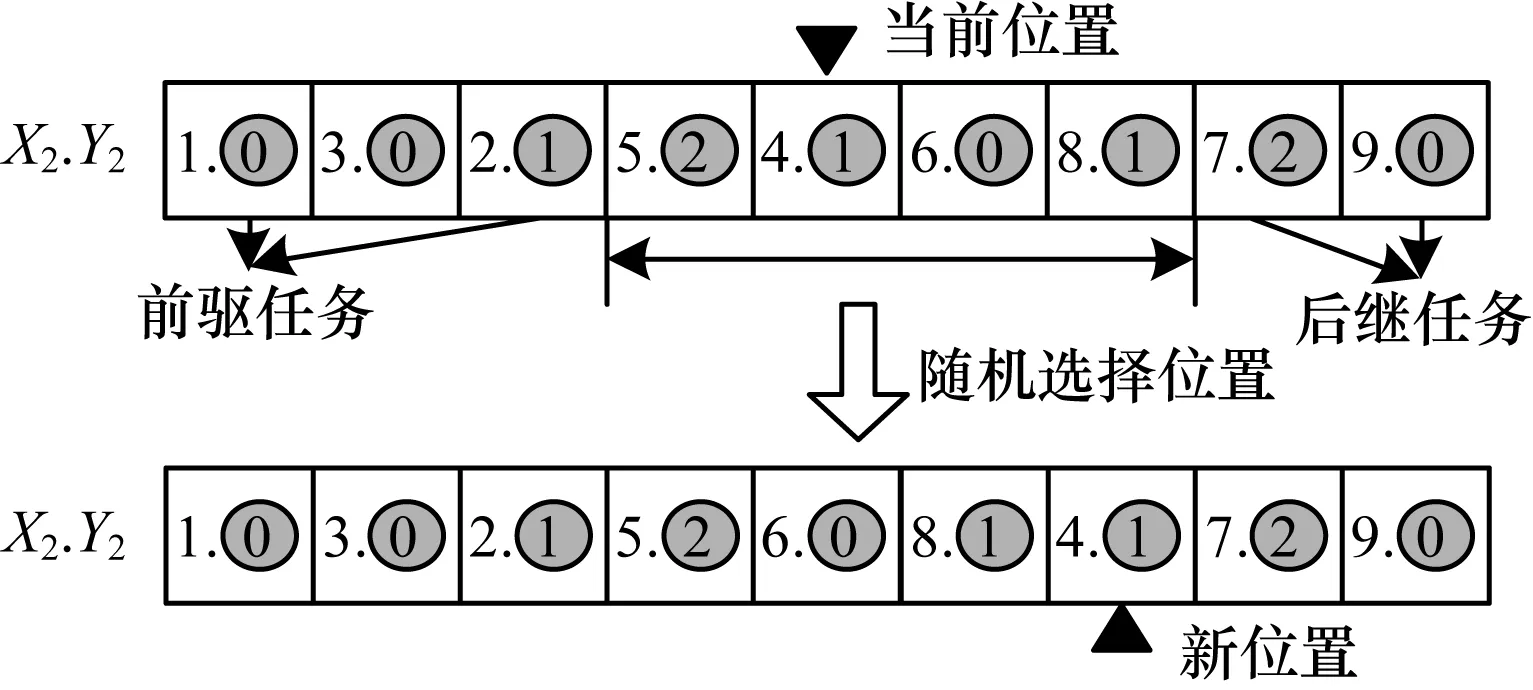
圖6 任務執行順序變異過程2Fig.6 Mutation process 2 of task execution sequence

算法2排序變異算法

輸入完成位置變異的任務序列

輸出完成整體變異操作的任務序列

Begin

1.生成[1,n-1]之間隨機數r;

2.for i=1 to r

3.搜索xr.yr的先序任務集{x1.y1,x2.y2,…,xa.ya};

4.end for

5.for i=r to n-1

6.搜索xr.yr的后繼任務{xb.yb,xb+1.yb+1,…,xn.yn};

7.end for

8.得到集合X′.Y′={xa+1.ya+1,xa+2.ya+2,…,xb+1.yb+1};

9.排出xr.yr當前位置,在集合X′.Y′中隨機選擇位置插入

10.得到新個體

End

5 仿真實驗與結果分析

本節對本文CAMEGA算法以及All-Local算法、Random算法、ECGA算法進行了仿真對比實驗。根據已有相關文獻,遺傳算法相關參數由表2[23]給出,網絡仿真參數由表3給出,其中,任務工作量為服從[1,200]之間均勻分布(單位為GHz),輸出數據量為服從[1,50]之間均勻分布(單位為MB)。

表2 遺傳算法相關參數

表3 網絡仿真參數

All-Local算法:將所有的任務都放在移動設備執行。

Random算法:在云輔助移動邊緣計算的計算卸載框架下,隨機分配任務的執行位置(本地、邊緣、云)和執行順序。

ECGA算法:移動邊緣計算的計算卸載框架下,基于遺傳算法的計算卸載算法。

5.1 任務數變化對系統總代價的影響

本節主要研究在不同的工作流任務數量下,CAMEGA算法、All-Local算法、Random算法、ECGA算法的性能比較,模擬的任務數分別為30、60、90、120和150的情況。如圖7所示,隨著工作流中任務數的增加,系統的總代價逐漸增加。與All-Local算法、Random算法、ECGA算法相比,CAMEGA算法的系統總代價最小,約為All-Local算法的8.4%、Random算法的43.7%、ECGA算法的30%。因此,在計算卸載問題中,CAMEGA算法有較大的優勢。

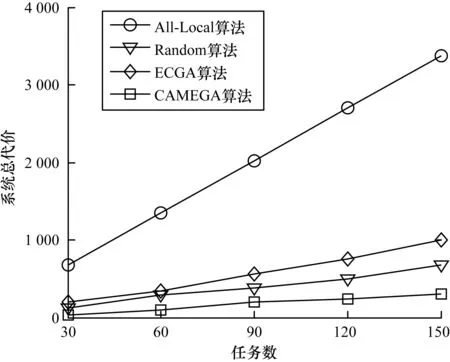
圖7 任務數變化對系統總代價的影響Fig.7 Impact of task number changes on total system cost

5.2 時延權重變化對系統總代價的影響

本節主要研究時延權重ω與能耗權重1-ω的比值大小在[0.01,100]時,CAMEGA算法、All-Local算法、ECGA算法與Random算法4種算法的性能比較。如圖8所示,針對不同的時延和能耗比值,本文提出的CAMEGA算法得到的結果明顯優于其他3種算法。因此,CAMEGA算法可以更好地適用于需求不同的移動服務。

圖8 時延權重與能耗權重的比值對系統總代價的影響Fig.8 Effect of ratio of delay weight to energy consumption weight on total system cost

5.3 迭代次數對系統總代價的影響

本節主要研究迭代次數在[10,100]時,迭代次數的變化對系統總代價的影響。取移動服務工作流中的任務數N=60,如圖9所示,隨著迭代次數的增加,All-Local算法得到的實驗結果幾乎沒有變化(略去),基于CAMEGA算法、Random算法、ECGA算法的系統總代價值呈下降趨勢,當迭代次數在[10,100]時,系統總代價的下降趨勢較大,迭代次數超過50以后,系統總代價的變化趨勢很小、趨于穩定。由此可以得出,迭代次數取50時,可以得到較優的實驗結果。

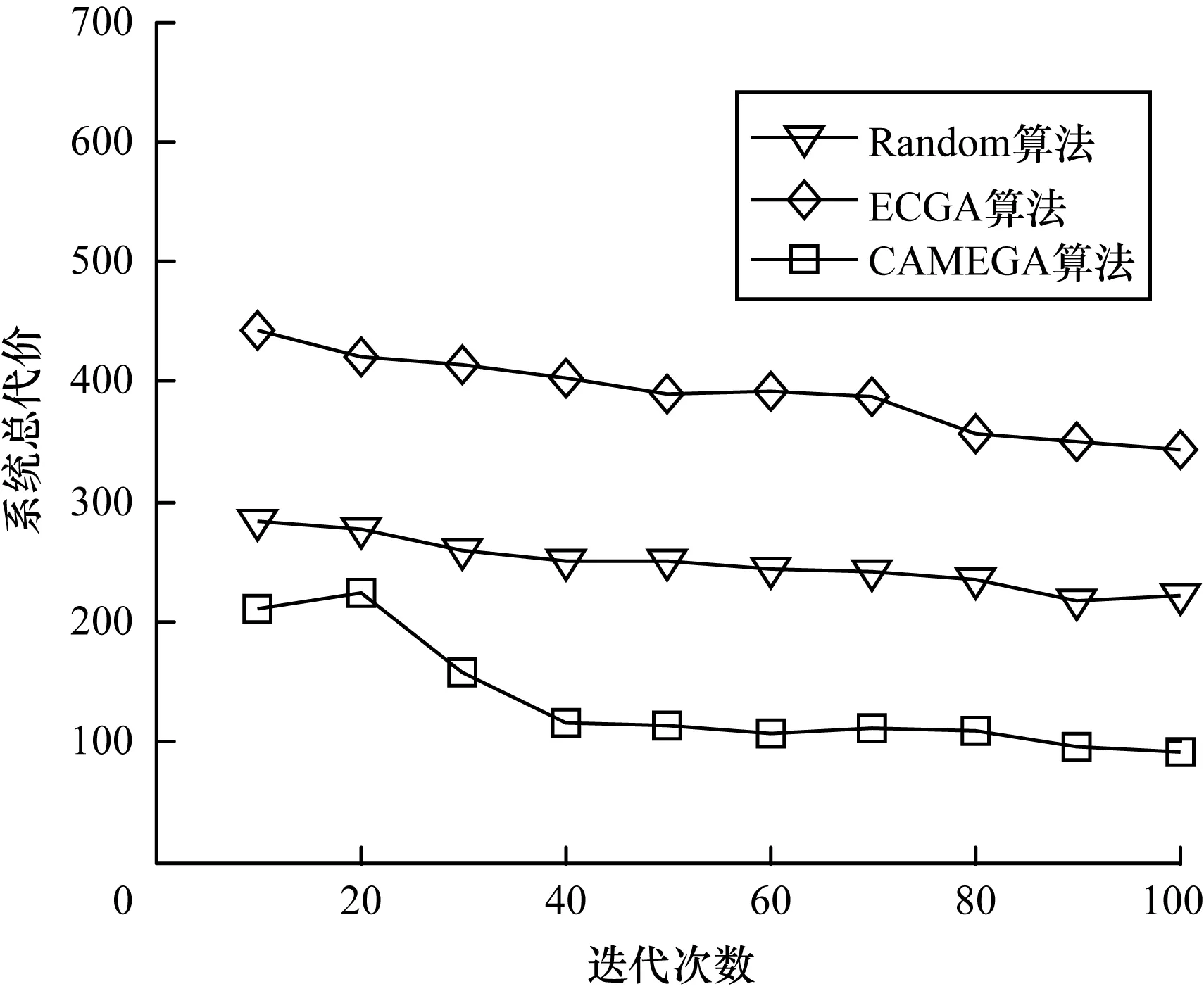
圖9 迭代次數對系統總代價的影響Fig.9 Impact of workload changes on total system cost

5.4 工作量變化對系統總代價的影響

本節主要研究任務工作量在[0,200]之間時系統總代價的變化。從圖10可以看出,隨著任務工作量的增加,系統總代價也在逐漸增加。這是因為在本地設備、邊緣服務器、云服務器的計算能力不變的情況下,增加任務的輸入數據量必然會導致執行時間變長,從而系統總代價變大。同樣,CAMEGA算法得到的系統總代價明顯小于All-Local算法、Random算法和ECGA算法。

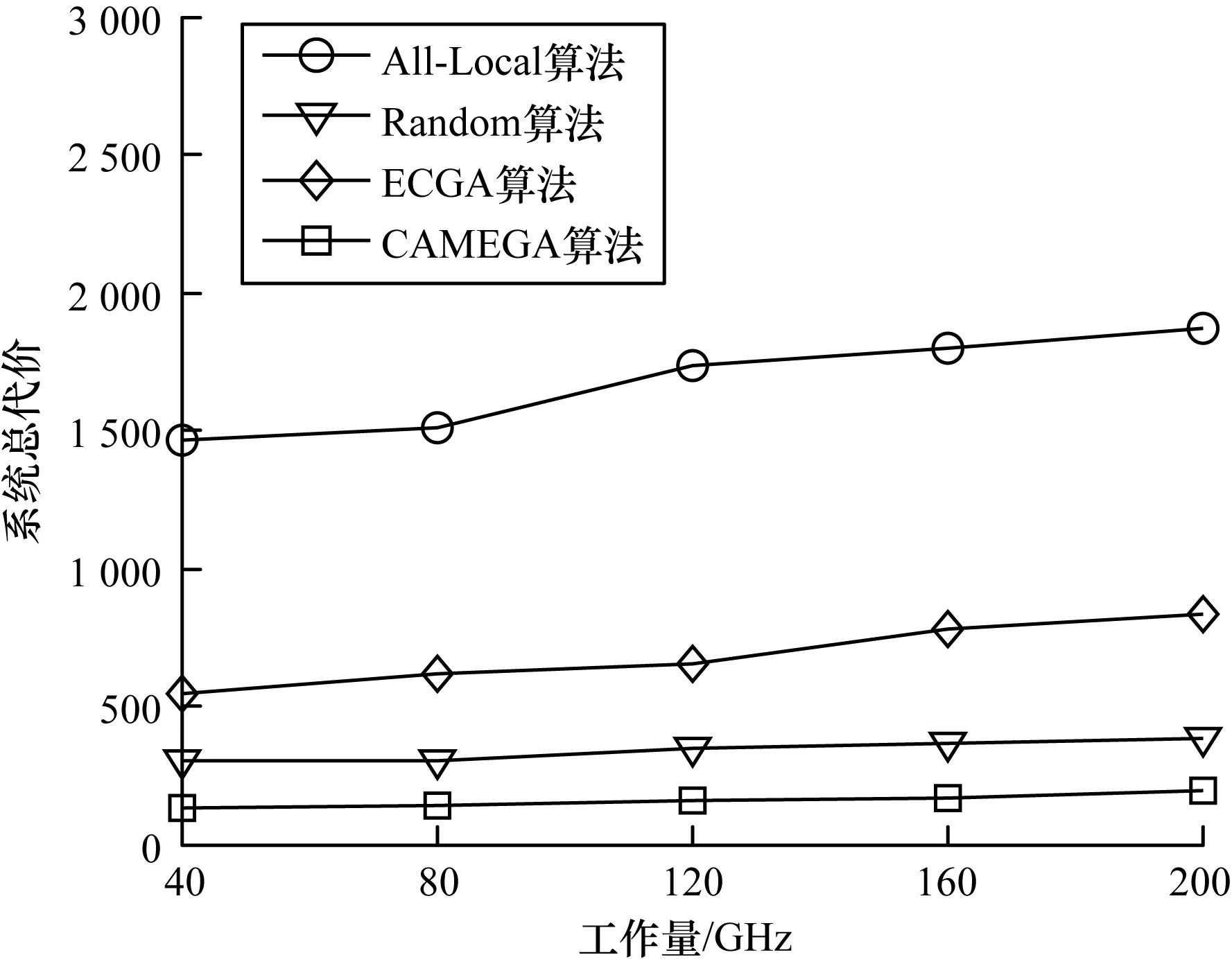
圖10 工作量變化對系統總代價的影響Fig.10 Impact of workload changes on total system cost

5.5 任務輸出數據量變化對系統總代價的影響

本節主要研究工作流任務的輸出數據在[10,50]時,4種算法的系統總代價的變化。如圖11所示,對于All-Local算法,隨著任務輸出數據量的增加,All-Local算法的系統總代價幾乎沒有變化,這是由于在All-Local算法中,移動服務中所有任務都在本地執行,不存在數據上傳/下載過程,也就不存在傳輸時延和傳輸能耗。對于Random算法、ECGA算法和CAMEGA算法,任務的輸出數據量越大,系統總代價越大。這是因為任務的輸出數據量對于工作流執行過程中的上傳/下載的時延和能耗都會產生較大的影響。在同樣的卸載策略下,較大的數據傳輸量會花費較長的時間。同樣,較大的數據傳輸量會給移動設備帶來更多的傳輸能耗。

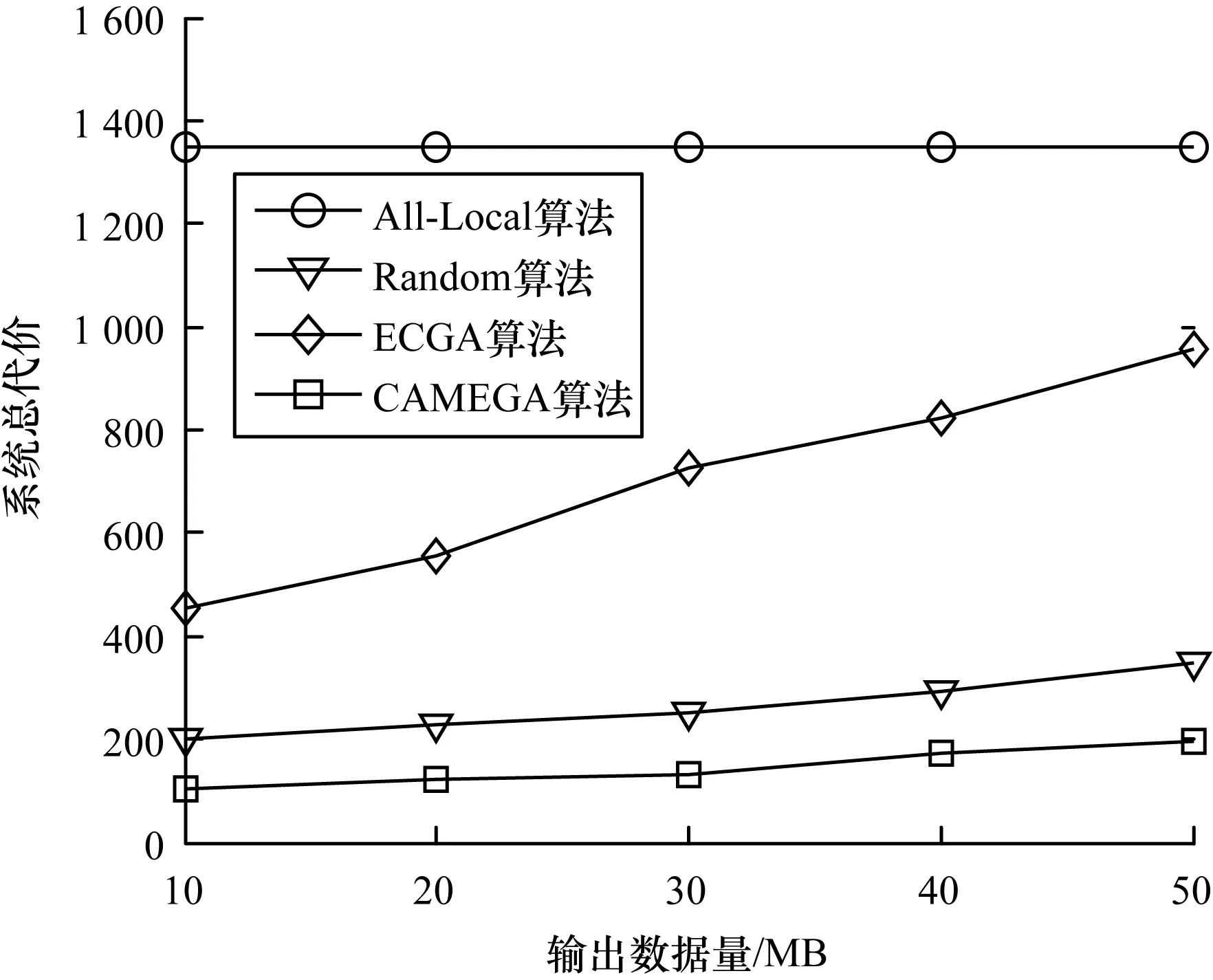
圖11 輸出數據量對系統總代價的影響Fig.11 Impact of amount of output data on total system cost

綜合上述分析可以看出,與All-Local算法、Random算法和ECGA算法相比,本文提出的CAMEGA算法均能得到最小的系統總代價。

6 結束語

本文針對移動服務的執行時間和移動設備能耗的優化問題進行研究,設計云輔助移動邊緣計算的計算卸載框架,并提出基于改進遺傳算法的計算卸載算法。通過選擇、交叉、變異等遺傳操作,迭代得到最優的卸載策略,實現系統總代價最小。仿真結果表明,與All-Local算法、Random算法和ECGA算法相比,CAMEGA算法系統總代價最小。下一步工作將對包含多個移動設備、邊緣服務器和云服務器等系統中的計算卸載問題進行研究。