一種改進的基于興趣相似度推薦算法

柯翔敏,陳 江,羅光華

(華僑大學 網絡與教育技術中心,福建 廈門 361021)

0 概述

目前,隨著物質生活的不斷豐富和科學技術的快速發展,人們的生活方式越來越多樣化。推薦算法的發展與運用使得用戶能夠快速發現自己感興趣的商品,從而在客觀上促進社會經濟的發展。

推薦算法可以分為基于內容的推薦[1]、基于協同過濾的推薦[2]以及混合推薦[3]三大類。其中,基于協同過濾的推薦算法應用最為廣泛,其又可分為基于用戶的系統過濾推薦、基于商品的協同過濾推薦[4]和基于模型的協同過濾推薦[5]。協同過濾推薦算法的思想是基于用戶-物品矩陣,如果為目標用戶進行推薦,選擇與目標用戶打分行為相似的Top-K個用戶打分過的物品,以及與目標用戶打分過的物品相似的Top-K個物品作為推薦候選。協同過濾推薦算法性能最重要的影響因素是相似度的計算方式。

在傳統的協同過濾推薦算法中,有余弦相似度、修正余弦相似度等常用的相似度計算方法。但是,由于用戶-物品矩陣存在數據稀疏性等問題[6-8],導致上述相似度計算方法存在相似度失真、相似度虛高、相似度難以區分等問題[9],進而造成推薦結果不準確的現象,影響了用戶體驗。

對于傳統協同過濾推薦算法相關度計算問題,一些學者提出了改進方式。文獻[10]考慮到傳統的相似度計算方法存在的數據稀疏問題,結合一些基礎相似度計算方法的優勢,將余弦相似度、杰卡德系數等相似度計算結果相結合并進行線性組合從而提高預測精度。文獻[11]引入元路徑、異構網絡的思想計算相似度。文獻[12]從3個方面對用戶相似度度量計算進行改進,其將用戶評分的平均差值引入到用戶相似度計算中。文獻[13]提出一種信任感知聚類的協同過濾方法。文獻[14]針對推薦系統中的數據稀疏性問題,提出一種比率相似度計算方法,該方法在計算用戶相似度時考慮2個用戶的所有偏好數據而非共同評分項。文獻[15]提出一種對協同過濾推薦算法進行改進的“用戶項目立方體”模型,該模型將相應的權重加入到時間因子中,然后用相應的權重計算相似度。文獻[16]為了降低稀疏性問題對相似度帶來的影響,利用LDA模型將高維空間轉化為低維空間,同時將相似度計算轉向低緯空間,從而降低了計算開銷。文獻[17]考慮到只有當不同用戶對相同項目都有很高的評分值時才能證明兩者之間具有很高的相似度,引入相似度改進因子和平衡因子的概念,重新計算相似度并對2個計算后的相似度進行加權處理。文獻[18]在局部敏感哈希算法的基礎上,提出基于精確歐氏局部敏感哈希的改進協同過濾推薦算法,其通過精確歐氏局部敏感哈希計算用戶的相似度,然后對用戶進行推薦。

上述改進的相似度計算算法均在一定程度上提高了推薦效果,但是多數算法都忽視了一個問題,即在用戶-物品矩陣中,不同物品對相似度的影響是不同的。在生活中存在一種現象,2個對冷門事物感興趣的人比2個對流行事物感興趣的人更有可能成為朋友,他們的相似度也更高。就事物本身而言,事物流行程度越低,對其感興趣的用戶的興趣權重分配值會越高。此外,以往的相似度計算算法同時也忽視了用戶之間共同感興趣的事物數量對用戶之間相似度的影響。為此,本文提出一種基于興趣分配與共同興趣項的相似度計算方法,并基于此構建一種混合協同過濾推薦模型,以提高推薦質量。

1 問題定義

1.1 逆流行度

定義1(逆流行度) 對于一個用戶-物品評分矩陣,物品存在逆流行度的特性,即物品的冷門程度的值位于0～1之間,該值越大表明物品的冷門程度越大。

通過上述定義可知,逆流行度是一個物品冷門程度的標準化值,其與流行度存在一種負相關的關系?，F有用戶-物品評分矩陣如表1所示,其中,5件物品被打分的次數分別為3、4、7、4、2,該數值即為流行度。

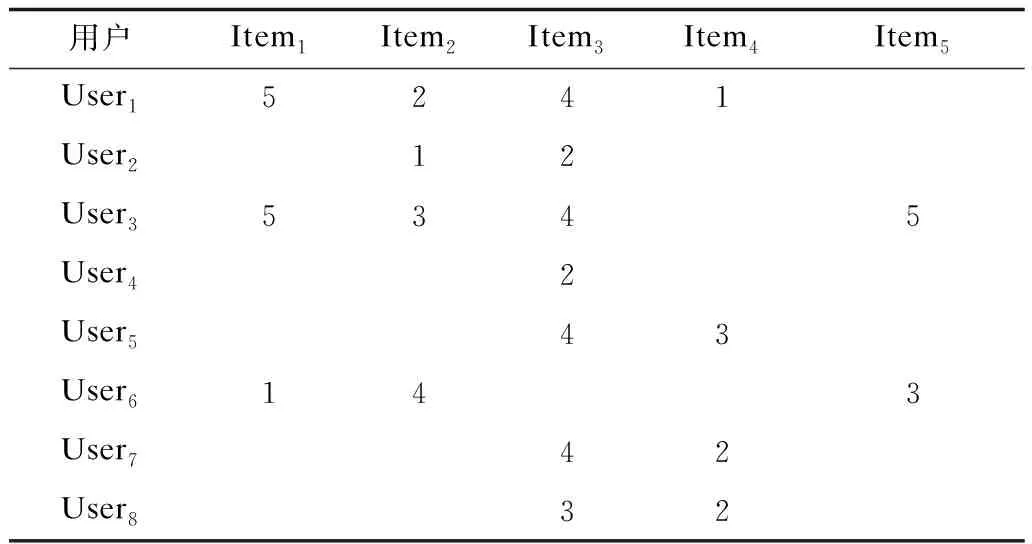
表1 用戶-物品評分矩陣Table 1 User-item rating matrix

流行度計算公式如下:

Pop(Itemi)=count(rating(j,i)>0),j∈U

(1)

其中,count為統計計算,U為用戶集合。

逆流行度是對物品冷門程度的一種度量方式,通過式(1)得到物品流行度之后,統計全局物品的流行度。對每一件物品進行逆流行度計算,逆流行度的度量方式如下:

(2)

其中,max與min計算可以分別得到物品中最大流行度與最小流行度的值。物品的逆流行度介于0～1之間,值越大,物品的冷門程度越大,其對興趣的潛在影響也越大。

1.2 共同興趣項

在一些傳統的相似度計算方法中,余弦相似度、修正余弦相似度都是對用戶的評分向量進行全量計算,如果2個用戶對某項物品均沒有評價,則該物品項在兩者的評分向量中為0。用戶-物品矩陣具有數據稀疏性,如果2個用戶評分項較少則可能會有很高的相似度。如果2個用戶即使對多數物品進行了評分,并且有許多為共同評分,但是余弦相似度的計算特性也可能會導致兩者的評分較低。本文認為如果用戶之間的共同評分項越多,他們擁有共同興趣的概率也就越大,用戶之間的相似度理應更高。但是,2個用戶對某一事物共同打分不一定代表兩者對該事物都有興趣,在5分為滿分的推薦系統中,如果一個用戶打5分,另一個用戶打1分,則這2個用戶對該事物的興趣差異很大。為此,本文提出共同興趣項的概念。

定義2(共同興趣項) 對于一個用戶-物品矩陣,如果用戶A與用戶B均對某一件物品I有評分操作,且A與B對I的評分都超過系統設定的興趣閾值α,則稱物品I為用戶A與用戶B的共同興趣項。

2個用戶之間的共同興趣項集合可用式(3)表示:

SA,B={i|rat(A,i)>α}∩{i|rat(B,i)>α}

(3)

其中,rat為評分值。

本文認為用戶之間的共同興趣項越多,且在共同興趣項中評分方差均值越小,則用戶之間的相似度越高。用戶的相似度應該通過用戶之間有多少共同的相似項來度量,因此,本文基于用戶的共同興趣項提出新的用戶相似度計算方法,如下:

(4)

其中,m為用戶A、B的共同興趣項數目,n為用戶-物品矩陣中物品的總數,T為一個常數,在式(4)中其為推薦系統中的評分最大值。

2 基于興趣分配與共同興趣項的協同過濾推薦

2.1 結合興趣分配的相關度計算

本文提出逆流行度與共同興趣項的概念以及相關度計算公式,在共同興趣項的基礎上提出一種新的相關度計算方法,但該方法并未結合逆流行度。本文提出逆流行度是考慮到生活中的“對冷門事物感興趣的人更可能成為好友,并且相似度更高”這樣一種場景。具體而言,對熱門事物產生過行為的用戶可能并非真正的偏好,也許是受一些社會因素的影響,比如媒體宣傳、營銷等。但是,如果用戶對冷門事物感興趣,一般是基于用戶本人的興趣偏好而受其他因素干擾較小?；谝陨戏治?本文在式(4)的基礎上結合共同興趣項的逆流行度進行相關度計算。存在2個用戶A、B,計算兩者共同興趣項的逆流行度的平均值,如式(5)所示:

(5)

其中,S為用戶A、B的共同興趣項集。R值越高,表示用戶的共同興趣項流行程度越低,共同興趣項對興趣分配的權重越高,受社會化的影響越小,即相似度越高。結合R值,本文提出新的相似度計算公式如下:

(6)

式(6)考慮到了用戶共同興趣的數量以及共同興趣項對相似度影響的權重,客觀合理,本文采用式(6)進行用戶之間的相似度度量。

2.2 混合協同過濾模型

通過式(6)可以完成用戶相似度計算,利用標準化方法可以將用戶相似度限定在0～1范圍內,對于目標用戶而言,可以生成相似用戶的Top-K推薦列表。但是,用戶-物品評分矩陣具有稀疏性問題,存在大量打分操作較少的用戶,且在評分矩陣中可能會有一些噪聲數據。本文為相似用戶的共同興趣項設定一個閾值,即當用戶之間的共同興趣項數量大于某閾值β時,用戶之間的相似度計算才有意義。如果只有少數共同興趣項則會存在一些不確定性,從而導致推薦結果不正確。因此,對于目標用戶A而言,其相似用戶列表為:

simUserList(A)={B|count(SA,B)>β}

(7)

如果2個用戶的共同興趣項數目小于β值,則其用戶相似度為0。

通過式(7)可以得到每一個用戶的相似用戶列表。此時會出現如下情況:一部分用戶會有較多的相似用戶,另外一部分用戶有較少的相似用戶,還有用戶的相似用戶列表甚至為空。對于此現象,本文提出一種混合協同過濾模型,具體如下:

1)對于第1種用戶,他們存在較多的相似用戶,因此,采用基于用戶的協同過濾模型,本文設置閾值為K。當相似用戶的數量大于K時,直接選取相似度排名靠前的前K個用戶作為候選推薦用戶,將相似用戶有過評分操作且目標用戶沒有評分操作的事物按照均分與相似度的綜合進行排序,選取前N個事物形成推薦列表返回給目標用戶。

2)對于第2種用戶,其相似用戶數量小于K且大于0,本文仍然采用基于用戶的協同過濾模型,但是要進行二次發掘來獲取更多的相似用戶,即與目標用戶相似的用戶的相似用戶也可能與目標用戶相似,如圖1所示。

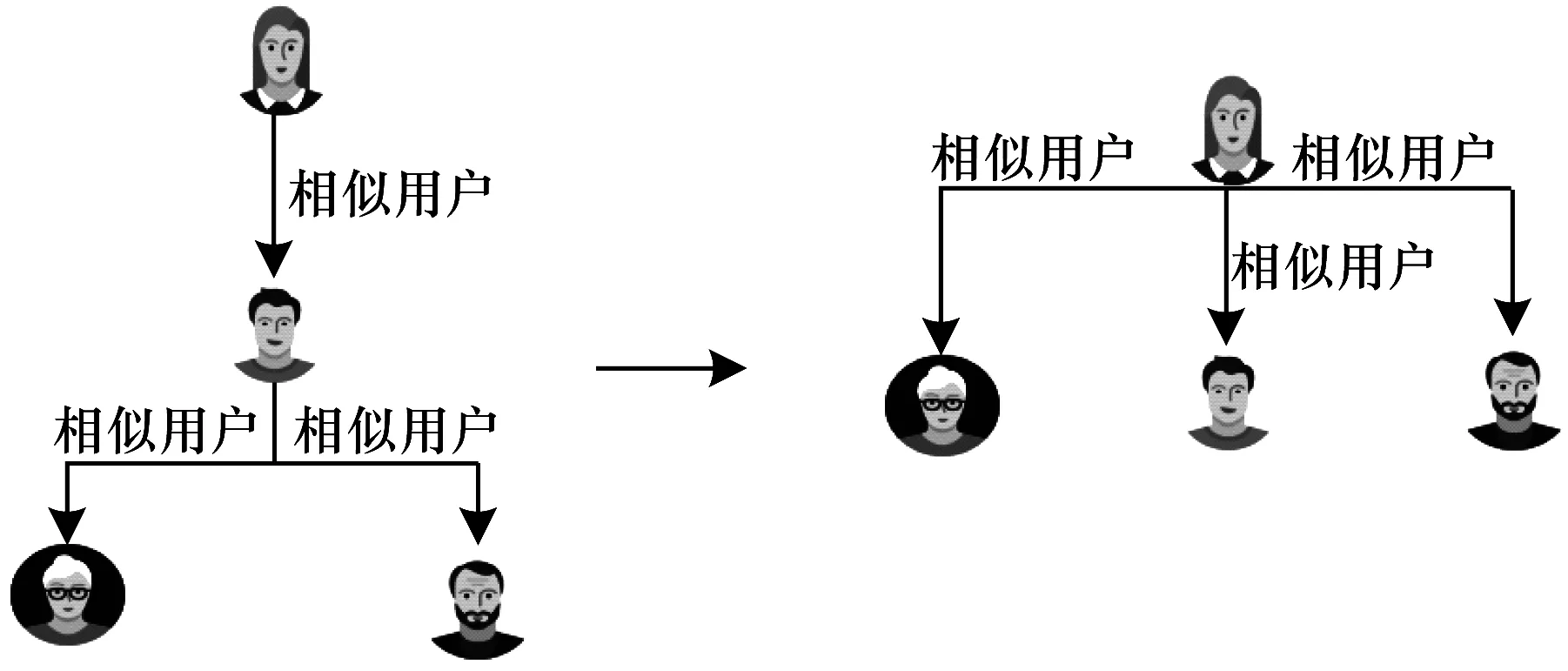
圖1 相似用戶二次發掘示意圖Fig.1 Schematic diagram of similar users’ secondary excavation

在目標用戶的相似用戶列表中引入相似用戶的相似用戶,如式(8)所示:

simUserList(A)=simUserList(A)∩simUserList(B)

(8)

其中,B是A的相似用戶。

對于通過二次發掘進入目標用戶相似用戶列表的用戶,其與目標用戶也有相似度的度量,如式(9)所示:

(9)

其中,n為Sim(B,C)>0的數量。

在完成二次用戶的二次發掘之后,即可采用第1種方式對用戶進行推薦。

3)針對第3種用戶,其沒有相似用戶。本文從2個方面對該類用戶進行分析,如果他們之間存在較多的興趣項,則采用基于物品的協同過濾模型進行推薦;如果他們之間有很少的興趣項或者沒有興趣項,則按照冷啟動的方式進行處理,可以選擇一些流行度高且評價較好的物品進行推薦。

對于每一個用戶,混合協同過濾推薦模型流程如圖2所示。

圖2 混合協同過濾推薦模型流程Fig.2 Procedure of hybrid collaborative filtering recommendation model

本文混合協同過濾推薦算法偽代碼如下:

算法1混合協同過濾推薦算法

輸入用戶集合U,物品集合I,相似用戶列表閾值K,共同興趣項過濾閾值β,興趣閾值α

1.begin

2.for each u in U:

3.simUserList(u)={}

4.recommendList(u)={}

5.for each u′ in U:

6.if u≠u′:

7.S(u,u′)={}

8.For i in I:

9.if rat(u,i)>α and rat(u′,i)>α:

10.S(u.u′).add(i)

11.if len(S(u,u′))>β:

12.simUserList(u).add([u′,Sim(u,u′)])

13.simUserList.sortBySim() //按相似度進行排序

14.if count(simuserList(u))≥K:

15.recommentList(u)=recommendByUser(simUserList(u))

16.elif count(simUserList(u))0:

17.for [u1,Sim(u,u1)] insimUserList(u):

18.simUserList(u)=simUserList(u)∩simUserList(u1)

19.recommentList(u)=recommendByUser(simUserList(u))

20.else:

21.recommentList(u) =recommendByItem(simUserList(u))

22.end

3 實驗結果與分析

3.1 數據集與實驗環境

本文選取推薦算法領域中的經典數據集MovieLens,原始數據集中包含用戶信息數據(User)、電影信息數據(Movie)與電影評價數據(Rating),本文實驗只選取電影評價數據集,大小約為21M,數據集基本信息如表2所示。

表2 MovieLens數據集信息Table 2 MovieLens dataset information

從表2可以看出,該數據集的稀疏程度為95.53%,稀疏程度較高。用戶的打分情況與電影被打分情況分別如圖3、圖4所示。

圖3 用戶打分統計Fig.3 User scoring statistics

圖4 電影得分統計Fig.4 Movie score statistics

從圖3、圖4可以看出,該數據集中用戶的評分情況與電影的得分情況均符合長尾分布,數據集中存在大量的“冷數據”。其中,評分操作高于電影總量10%的用戶約占用戶總數的10%,如果僅以改進的基于用戶的協同過濾推薦模型進行推薦,可預見存在一些用戶列表為空的用戶。因此,本文提出的混合協同過濾推薦模型具有現實意義。

本文實驗環境設置如下:操作系統為Windows7 64位系統旗艦版,CPU為Intel?CoreTMi5-7500 3.40 GHz,內存為8 GB。

3.2 實驗評價指標

推薦算法的目的是向用戶推薦其可能感興趣的事物,而非預測用戶會對事物如何評分[19-20],基于此思想,本文采用Top-N推薦方法,而不采用RMSE、MAE等基于回歸模型的評價指標,從而為用戶生成推薦列表。本文將精確率(precision)、召回率(recall)與F1值作為實驗評價指標,3個評價指標的計算公式分別如下:

(10)

(11)

(12)

其中,U為用戶集合,Ru表示對用戶u的推薦列表,Iu表示目標用戶喜愛的物品集合,用戶感興趣的評價標準可由前文中共同興趣項的分數閾值表示。

以MovieLens數據集為例,精確率表示推薦成功的電影占推薦電影總數的比例,召回率表示推薦成功的電影占用戶感興趣的電影的比例。

3.3 結果分析

本文將數據集分為訓練集與測試集,因為評分數據集中存在時間戳特征,鑒于推薦算法的時間特性,即用戶對物品的興趣值受時間影響,本文將訓練集與測試集按時間劃分,時間靠前的前80%數據為訓練數據,余下為測試數據。實驗中采用的對比算法為3種協同過濾算法,分別記為Cosin、Corrcosin和Pearson,三者分別采用余弦相似度、修正余弦相似度和皮爾遜系數進行相似度計算,將本文相似度計算方法記為New。

1)相同參數下不同推薦算法的比較

本次實驗比較推薦列表數目為20、每個用戶的相似用戶列表K值為20時各算法的性能,實驗計算每批次500個用戶的精確率與召回率,共取10個批次的平均值作為評價指標結果。從圖5可以看出,本文混合協同過濾推薦算法的精確率、召回率與F1值3個評估指標均優于其他3種基線算法,基于修正余弦相似度的推薦算法效果最差。

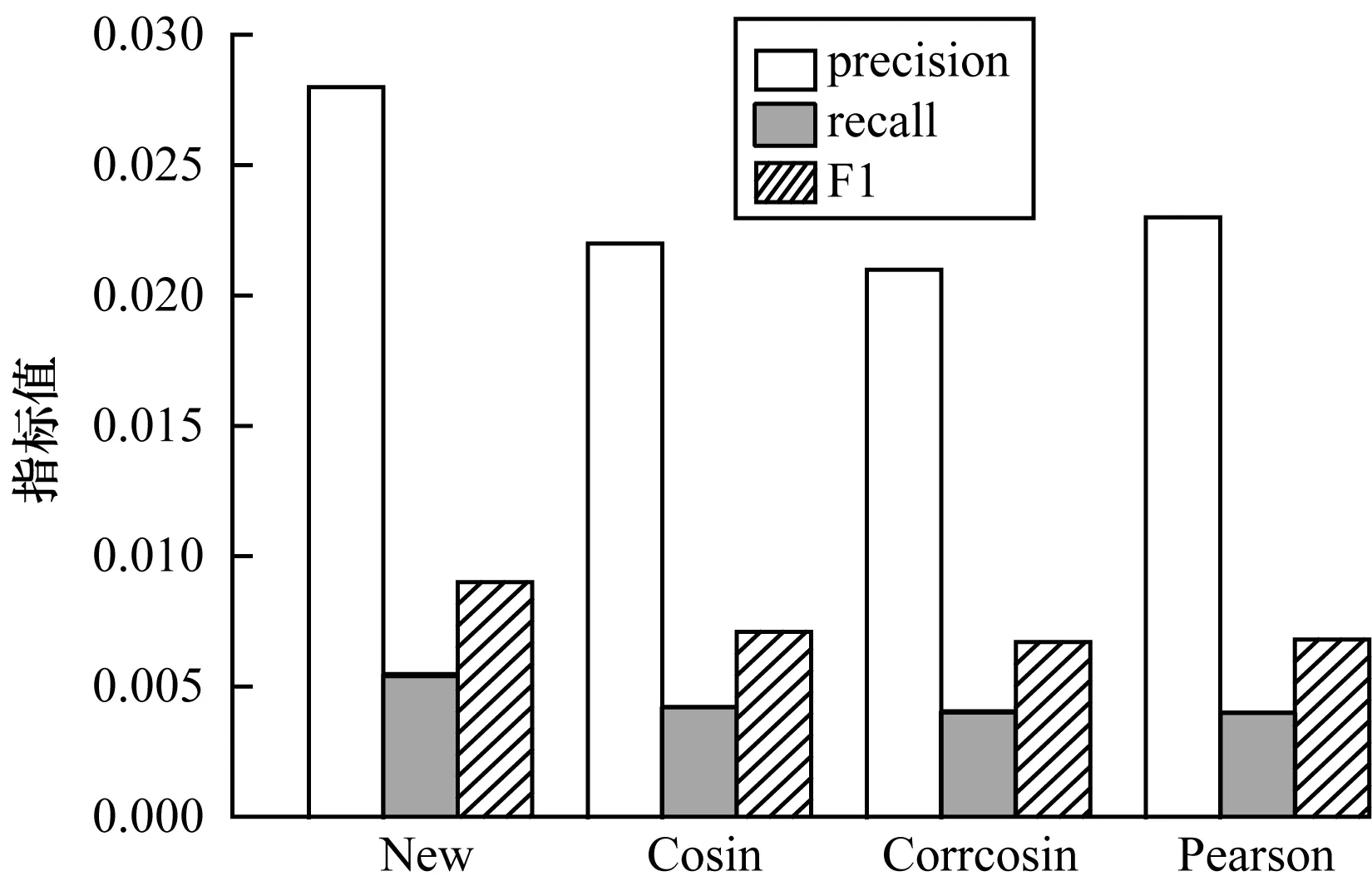
圖5 不同推薦算法的評估指標結果Fig.5 Evaluation index results of different recommendation algorithms

2)不同參數對推薦算法的影響

(1)推薦列表長度N。本次實驗比較最相似用戶的K值一定時(本實驗中K=20)推薦列表長度對推薦效果的影響。實驗進行10個批次,每個批次隨機選擇500個目標用戶,每個批次對用戶的推薦列表長度以增量為5進行劃分。

從圖6可以看出,隨著推薦列表長度的增加,精確率總體比較平穩,在N<35時,精確率有一定的提升,但N超過35之后,精確率開始下降,其他2個指標在N取5～50值時都有相對較高的提升,特別是F1值,其在N值為5～40時與推薦列表長度呈正相關關系。在圖7中,本文比較不同的推薦列表長度下4種協同過濾推薦算法的F1值大小。從圖7可以看出,在推薦列表長度為5～15時,不同相似度計算算法的推薦效果幾乎相同,當推薦列表長度增加后,本文相似度計算算法的F1值優于對比推薦算法,并且隨著推薦列表長度的進一步增加,本文相似度計算算法與修正余弦相似度計算算法明顯優于其他2種相似度計算算法。

圖6 推薦列表長度對推薦效果的影響Fig.6 Effect of recommendation list length on recommendation effect

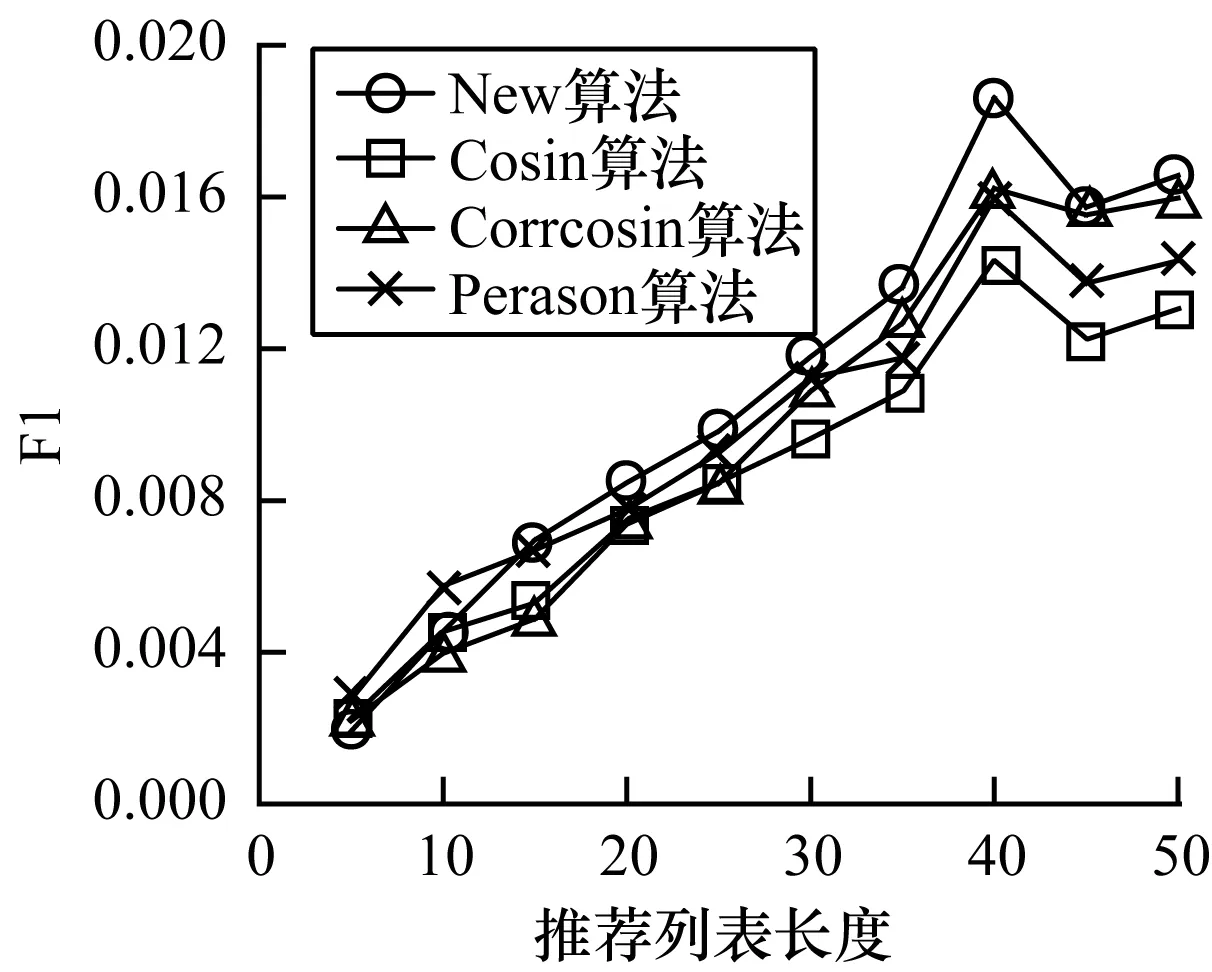
圖7 4種相似度計算算法在不同列表長度下的F1值Fig.7 F1 values of four similarity calculation algorithms under different list lengths

(2)最相似用戶列表長度K。在推薦列表長度一定時,分析最相似用戶列表長度對推薦效果的影響。實驗過程同樣進行10個批次,每個批次隨機選擇500個目標用戶,每個批次對用戶的推薦列表長度以增量為5進行劃分。在推薦列表長度為定值的情況下,不同的相似用戶列表長度對推薦結果的影響較小。由圖8可以看出,精確率、召回率與F1值3條曲線變化比較平穩。在K=25時,3個評估指標均達到最大。然后,隨著K值的增大,3個指標均有所下降,不過整體變化不大。綜上,推薦列表長度對推薦結果的影響大于最相似用戶列表長度。

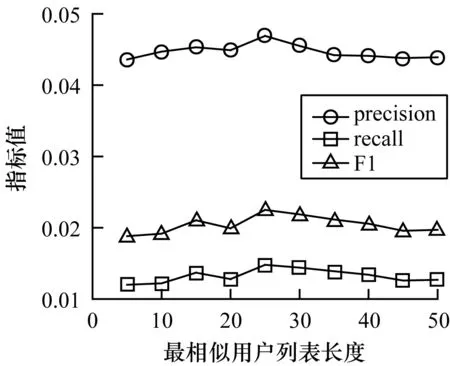
圖8 最相似用戶列表長度對推薦效果的影響Fig.8 Influence of the length of the most similar user list on the recommendation effect

3.4 算法性能分析

比較本文相似度計算算法與其他相似度計算算法在同樣硬件條件與實驗參數下,計算不同量級用戶之間相似度所消耗的時間,10次實驗的平均結果如表3所示。從表3可以看出,本文相似度計算算法計算效率最高,其次是Cosin和Pearson算法,兩者時間開銷基本一致,時間開銷最大的是Corrcosin算法,大約為本文算法的20倍。本文相似度計算算法在時間性能上有較大優勢,原因是本文算法設置一個共同興趣項的閾值,用戶達到閾值后會被認為是好友,一個用戶的好友列表平均值肯定小于其他相似度計算算法。在基線相似度計算算法中,用戶列表會考慮全部用戶并進行排序,用戶相似度的排序會消耗大量時間。

表3 相似度計算算法時間性能比較Table 3 Time performance comparison of similarity calculation algorithms s

4 結束語

本文針對基于協同過濾的推薦模型中原有相似度計算方法存在一定失真性的問題,結合事物流行度對用戶興趣權重分配與用戶共同偏好事物數目的影響,設計一種新的用戶相似度計算方法,并在該方法的基礎上構建一種混合協同過濾推薦模型。實驗結果表明,該模型的推薦效果優于基于基線相似度計算方法的推薦模型。下一步將針對用戶推薦時的數據稀疏性與冷啟動問題,結合更多影響相似度的潛在因素來提高推薦效果,并優化推薦算法的多樣性與覆蓋率等其他指標。此外,協同過濾推薦算法普遍存在復雜度較高的問題,且本文混合推薦模型涉及較多的參數,因此,進行高效調參調優以降低算法復雜度也是今后的研究重點。