氣浮軸承均壓腔內圓角結構對振動特性影響的實驗研究*
武 靜,錢俊兵,袁銳波*
(1.昆明理工大學 機電工程學院,云南 昆明 650500;2.昆明理工大學 民航與航空學院,云南 昆明 650500)
0 引 言
因具有低摩擦、低功耗、高精密、無污染等優點,氣浮軸承被廣泛應用于半導體、超精密測試設備和高精密加工機床設備等領域[1-2]。然而隨著設備精度的要求不斷提高,氣浮軸承的微振動制約著其運動定位精度的進一步提升,使制造加工精度無法更高。
為研究自激振動的起因和抑制方法,國內外學者做了大量研究。KAWAI等[3]認為是由于結構中微觀粗糙表面誘發氣體湍流而引起的自激微振動;SAWADA等[4]對氣浮導軌的性能進行了分析,發現了導軌結構對振動的影響;AL-BENDER等[5]總結了描述氣浮軸承壓力氣膜的各種方法,提出了主動補償措施提高軸承穩定性;CHEN等[6]提出了有腔小孔節流氣浮軸承在節流孔出口處存在氣旋,并提出了氣旋會引起氣膜振動的觀點,對比了多種氣腔內的氣體流動特性,提出了球形腔結構能有效抑制氣浮軸承的微振動的觀點;李運堂等[7]運用了LES方法分析了小孔節流氣浮軸承內的氣體流動特性,研究證實了氣浮軸承發生自激振動主要是氣旋的產生和破裂;陳琦等[8]提出了在氣浮軸承工作表面增加均壓槽的方法來抑制軸承的微振動;杜建軍等[9]以圓周方向有均壓槽的氣浮軸承為研究對象,分析得到了氣錘振動穩定的判別方程;龍威等[10-11]分析了軸承內部氣膜波動形成機理,發現了氣膜流場內氣旋分布規律與軸承微振動有著密切關系,并通過實驗得到了沿氣膜高度方向的振動是導致氣浮軸承微振動的主要因素的結論;薛義璇等[12]通過仿真分析發現了氣浮軸承氣腔帶倒角的結構能提高軸承的穩定性。
綜上所述,雖然對于氣浮軸承微振動特性的研究一直是關注熱點,很多學者也分析了它的形成機理,但目前還沒有關于均壓腔內圓角結構對氣膜振動特性影響的實驗研究。
本文將通過設計實驗方案,采集氣浮軸承氣膜的振動數據,分析均壓腔內圓角結構對氣膜振動特性的影響,為超精密靜壓氣浮軸承的設計提供一定的參考。
1 氣浮軸承實驗
氣浮軸承的工作原理示意圖如圖1所示。
圖1中,高壓空氣經進氣道進入節流孔小孔節流后,進入均壓腔環面二次節流,再進入軸承底部與支承平臺形成的微小間隙(即氣膜間隙)向周邊擴散,最后經過軸承邊緣排出大氣。
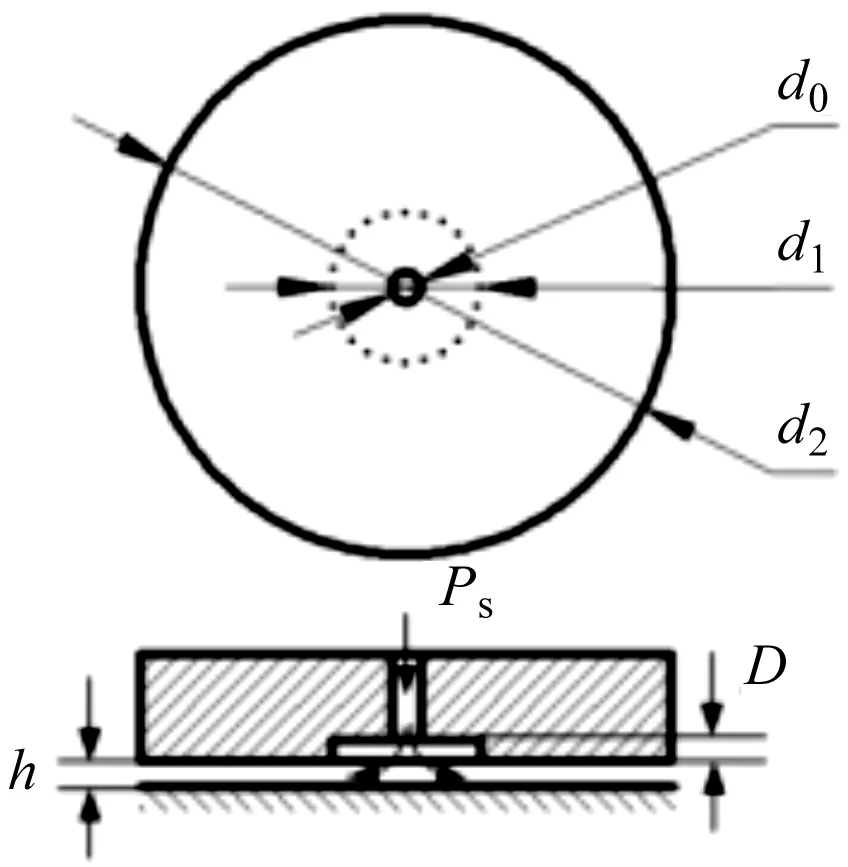
圖1 氣浮軸承工作原理示意圖
由于氣膜間隙十分微小,間隙內的壓力始終大于大氣壓力,氣膜具有一定承載能力。
1.1 實驗原理和裝置
為了實現對氣浮軸承微振動信號的測量,筆者研究其振動特性。
具體是將氣浮軸承作為測試對象,供氣孔與軸承氣道連通,通過電感測微儀實時測量氣膜厚度,加載氣缸壓力改變氣膜厚度,將氣膜間隙控制在10 μm,再通過LMS動態檢測儀將加速度傳感器采集到的振動型號傳輸到PC端。
氣膜微振動實驗原理圖如圖2所示。
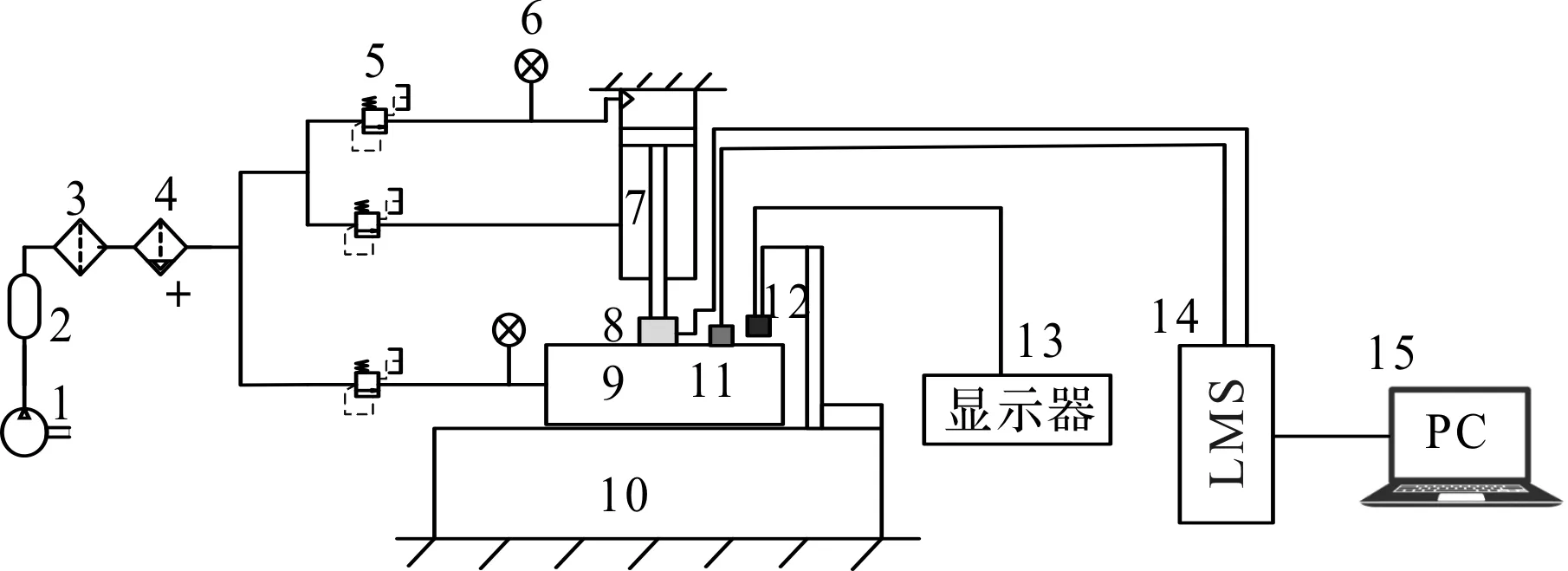
圖2 氣膜振動測試實驗原理圖1—空壓機;2—氣罐;3—過濾裝置;4—油霧分離器;5—減壓閥;6—壓力表;7—氣缸;8—動態力傳感器;9—氣浮軸承;10—大理石隔振平臺;11—加速度傳感器;12—電感測微儀;13—電感微位移顯示器;14—LMS動態監測儀;15—計算機
在整個實驗中,由空壓機提供氣源。其中:
過濾調壓閥的型號為SMC AW30-03D-A,油霧分離器的型號為SMC AFM30-03D-A;
減壓閥的型號為SMC IR2020-02,其設定壓力范圍為0.01 MPa~0.8 MPa;
氣缸的型號為SC63X,滿足使用壓力范圍(0.1 MPa~1.0 MPa);
動態力傳感器的型號為BSHS-1(量程0~150 kg);
PCB加速度傳感器型號為352A24 SN LW195334;
LMS動態監測儀進行振動數據的實時采集和記錄,頻率采集范圍為0~40 MHz,掃描精度±2%。
電感測微儀為DGC-8ZG/D型微位移傳感器,其分辨率為0.01 μm,顯示誤差在±0.05 μm;電感微位移顯示器的型號為DGS-6C。
微振動測試裝置實物圖如圖3所示。

圖3 微振動測試裝置實物圖
1.2 實驗條件與方法
為了研究均壓腔內圓角結構對軸承振動特性的影響,筆者設計了不同節流結構的氣浮軸承。
節流方案局部圖如表1所示。

表1 節流結構方案局部圖
表1中,筆者以均壓腔無圓角連接的小孔節流氣浮軸承(S-type結構)、節流孔出口(即均壓腔入口)處圓角連接的氣浮軸承(R-type1結構)和均壓腔出口圓角連接的氣浮軸承(R-type2結構)3種結構的氣浮軸承為實驗對象。
其中,節流孔直徑d0=0.15 mm,均壓腔直徑d1=6 mm,軸承直徑d2=60 mm,均壓腔深度D=0.1 mm。
其中,R-type1和R-type2結構中圓角結構為半徑R=0.05 mm的圓弧。
實驗環境溫度為25 ℃;軸承供氣壓力Ps為0.2 MPa~0.6 MPa。適當加載氣缸壓力,使氣膜間隙厚度保持在h=10 μm。
本文對保持氣膜間隙穩定后的S-type結構、R-type1結構和R-type2結構的氣浮軸承進行振動測試,使用LMS動態檢測儀采集其振動數據,經過多次測量比較,保證數據的準確性。
2 數學模型
氣浮軸承節流孔和均壓腔內氣體是復雜的湍流運動,均壓腔內的氣旋導致氣膜內氣體流速的改變,由于壁面剪切作用與氣體流速的變化,使得節流孔出口處產生氣旋渦,而在遠離節流孔出口處會產生氣旋渦的破裂或分解。
由氣體靜壓潤滑理論可知,氣浮軸承內氣體流場的連續性方程可以用Navier-Stokes(N-S)方程[13]表示,即:
(1)
式中:p—氣體壓強;μ—氣體動力粘度;u—x方向上的速度分;v—y方向上的速度分量;w—z方向上的速度分量;ρ—氣體密度。
根據氣體為定常流動,以及氣膜區域內部沿氣膜厚度方向壓力p與z坐標無關等條件,可以得到氣體在氣膜間隙內流動的簡化氣體的動量方程式[14],即:
(2)
當模型結構發生改變時,軸承內部的邊界也隨之改變,此時常用的N-S方程將不能很好地表達出軸承邊界氣體滑移流動特性和內部壓力分布特征;根據廣義Maxwell速度滑移邊界理論,此時需要添加速度滑移邊界條件[15-16],即為:

(3)

(4)
式中:λ—邊界滑移長度;h—為氣膜高度;U—軸承氣膜的表面速度。
當軸承結構改變時,邊界滑移長度λ也隨之改變,直接影響速度分量u、v、w的大小。且由式(4)可知,λ對豎直方向的速度分量w影響最大。
在有腔小孔節流氣浮軸承中,均壓腔內氣旋的變化是引起軸承微振動的主要因素,而氣旋的變化是由腔內流體的速度變化而引起的,即可以通過改變邊界條件來削減軸承的振動強度。
所以筆者通過改變邊界條件,即改變軸承結構的方法來探究削減軸承微振動的措施。
3 實驗結果及分析
在靜態穩定工作條件下,為研究S-type、R-type1和R-type2結構的氣浮軸承內部氣膜的振動特性,筆者設計了實驗方案,采集了3種不同結構氣浮軸承的振動信號,分析了3種結構在不同供氣壓力的微振動幅值及頻域特性的變化規律,對比分析了均壓腔內圓角結構及圓角位置對振動特性的影響。
由于相比沿氣膜平面豎直方向,沿氣膜平面半徑方向的微振動的影響較小,筆者主要研究沿豎直方向的微振動幅值及頻域變化。
3.1 時域分析
通過實驗可以讀取10 s內軸承的振動幅值變化的平均值,在供氣壓力0.2 MPa~0.6 MPa時,筆者分別記錄3種結構的氣浮軸承的振動幅值,繪制出的不同供氣壓力下的振動幅值變化,如圖4所示。
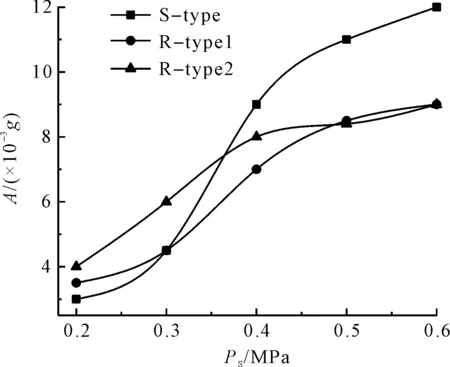
圖4 不同供氣壓力下的振動幅值變化曲線
從圖4可以看出:
(1)當供氣壓力由0.2 MPa增加至0.6 MPa時,S-type結構的振動幅值A從3×10-3g增加至12×10-3g;R-type1結構的振動幅值A從3.5×10-3g增加至9×10-3g;R-type2結構的振動幅值A從4.0×10-3g增加至9×10-3g;
(2)隨著供氣壓力增大,3種結構的氣浮軸承沿氣膜平面豎直方向的微振動幅值也隨之增大,即氣浮軸承的微振動強度隨著供氣壓力的增大而增大;
(3)當供氣壓力小于0.3 MPa時,S-type結構的微振動強度(3×10-3g~4.5×10-3g)小于R-type1結構(3.5×10-3g~4.5×10-3g)和R-type2結構(4×10-3g~6×10-3g)的微振動強度;
(4)當供氣壓力大于0.3 MPa后,S-type結構的微振動強度隨著供氣壓力的增大,大幅增加由4.5×10-3g增加至12×10-3g,R-type1結構和R-type2結構的微振動強度分別由4.5×10-3g和6×10-3g增加至9×10-3g。
由此可以明顯看出:R-type1結構和R-type2結構能減緩由于供氣壓力增大而導致軸承微振動的增強。
這是由于:
(1)當供氣壓力低(Ps≤0.3 MPa)時,氣膜間隙內的氣流速度較低,產生的氣旋強度較弱,此時的振動大部分是由氣浮軸承結構和實驗平臺共振所引起的;
(2)當采用較高供氣壓力(Ps≥0.4 MPa)時,軸承氣膜間隙內氣流所攜帶的能量也較大,此時由氣膜內氣旋運動而引起的振動也不容忽視,但是R-type1結構和R-type2結構均壓腔內存在圓角連接,可以起到過渡引流的作用,在一定程度緩解了節流孔出口處或均壓腔出口處由于氣體流動橫截面積的擴大,而導致氣體急劇變化引起的軸承振動。
綜上所述,均壓腔內圓角結構的存在能減緩因供氣壓力過大而引起的軸承微振動,即在高壓環境下,均壓腔內采用圓角連接結構的氣浮軸承的穩定性優于沒有采用圓角連接結構的軸承。
3.2 頻域分析
實驗完成后,提取軸承振動的頻域信號。
在不同供氣壓力下,筆者研究的3種結構的氣浮軸承的頻域信號如圖5所示。

圖5 不同供氣壓力下的頻域信號
其峰值頻率如表2所示。

表2 3種結構峰的值頻率對比表
從圖5和表2可以看出:在相同氣膜厚度(h=10 μm)時,同一結構的氣浮軸承的微振動有著相似的頻率特征,隨著供氣壓力的增大,微振動強度也在增大,但產生峰值的幾個頻率點基本是重合的。
對于不同結構的氣浮軸承,雖然產生的峰值的頻率點不一致,但產生最大峰值的主頻段基本都在4 kHz附近,具體情況為:
(1)對于S-type結構,峰值頻率主要集中在0.98 kHz、3.8 kHz、5.3 kHz、19.8 kHz等一系列頻段內,振動幅值最大處即主頻段在3.8 kHz頻段處;
(2)對于R-type1結構,峰值頻率主要集中在0.63 kHz、2.0 kHz、4.1 kHz、19.3 kHz等一系列頻段內,主頻段在4.1 kHz頻段處;
(3)對于R-type2結構,峰值頻率主要集中在0.75 kHz、1.8 kHz、3.5 kHz、19.9 kHz等一系列頻段內,主頻段在3.5 kHz頻段處。
雖然對于R-type1結構和R-type2結構,在20 kHz頻段內振動幅值有一定增長,但其增長幅值較小,也不易產生共振。
上述實驗結果表明:隨著供氣壓力的增大,會使軸承內部的微振動強度增強,而均壓腔內圓角連接的結構能減緩氣流與軸承壁面的沖擊,雖會使高頻段的振幅有些許增大,但抑制了主頻段內的幅值增長,從而降低了氣膜內的振動強度。
4 結束語
通過搭建相關實驗平臺,筆者采集了傳統有腔小孔節流氣浮軸承(S-type結構)和均壓腔內圓角連接結構的氣浮軸承(R-type1結構和R-type2結構)的振動信號,對比分析了其時域信號和頻域信號,并得到了以下主要結論:
(1)分別對比均壓腔內無圓角結構、節流孔出口圓角連接結構和均壓腔出口圓角連接結構的時域信號可知,隨著供氣壓力的增大,三者的振動強度都增大,但節流孔出口圓角連接結構和均壓腔出口圓角連接結構的振幅增長較小,且當供氣壓力超過某定值時其振動幅值趨于平穩,即均壓腔內圓角連接結構能有效削減因供氣壓力增大而導致的振動;
(2)對比均壓腔內無圓角結構、節流孔出口圓角連接結構和均壓腔出口圓角連接結構的頻域信號可知,雖然三者結構產生峰值的頻率點不一致但產生最大峰值的主頻段都在4 kHz附近,即均壓腔內圓角連接結構對振動的共振頻率影響較小,對振動幅值的影響更大;
(3)對比節流孔出口處圓角連接結構和均壓腔出口圓角連接結構可知,當供氣壓力超過0.5 MPa時,兩種結構的振幅基本一致,即當高壓工作時均壓腔內圓角位置對振動的影響很弱;當供氣壓力低于0.5 MPa時,節流孔出口處圓角連接結構的振動強度較低,即節流孔出口圓角連接結構削減振動的效果更佳。

