基于θ-映射法的ZSGH4169合金缺口試樣蠕變變形模擬
李 迪1,魏大盛
(1.中國航發(fā)商用航空發(fā)動(dòng)機(jī)有限責(zé)任公司,設(shè)計(jì)研發(fā)中心,上海 201108;2.北京航空航天大學(xué)能源與動(dòng)力工程學(xué)院,北京 100191)
0 引 言
蠕變是指在一定溫度下金屬受持續(xù)應(yīng)力作用而產(chǎn)生緩慢塑性變形的現(xiàn)象,是溫度、應(yīng)力和時(shí)間共同作用的結(jié)果[1]。蠕變研究一般從兩方面著手:一是從微觀角度出發(fā),研究蠕變機(jī)理及冶金因素對蠕變特性的影響,以提高金屬的蠕變抗力;二是從唯象角度出發(fā),以試驗(yàn)為基礎(chǔ),根據(jù)觀察到的宏觀蠕變現(xiàn)象建立蠕變方程,并尋求工程上的應(yīng)用。從蠕變速率來看,蠕變曲線包括速率減小、速率恒定、速率增加3個(gè)階段。研究人員根據(jù)材料在蠕變試驗(yàn)中表現(xiàn)出來的不同特征,建立了多種蠕變模型,如Norton率模型[2]以及在其形式上發(fā)展而來的時(shí)間硬化/應(yīng)變硬化模型、Omega模型[3-4]、θ-映射法模型[5-6]等。這些模型特點(diǎn)鮮明且具有特定的適用范圍:Norton率模型只能描述第一階段和第二階段的蠕變變形;Omega模型是針對特征明顯的第三階段蠕變曲線建立的;θ-映射法模型可以描述完整的蠕變過程,且參數(shù)組合較為靈活,在工程上應(yīng)用較多[7]。
對于實(shí)際工程結(jié)構(gòu),如航空燃?xì)廨啺l(fā)動(dòng)機(jī),其熱端部件(渦輪盤、渦輪葉片等)在高溫、高載荷作用下通常會(huì)發(fā)生蠕變變形,成為結(jié)構(gòu)失效的隱患。因此,航空燃?xì)廨啺l(fā)動(dòng)機(jī)設(shè)計(jì)時(shí)需要對蠕變行為進(jìn)行深入分析[8],并針對蠕變可能導(dǎo)致的失效模式給出相應(yīng)的設(shè)計(jì)準(zhǔn)則。然而,螺栓孔邊、圓角、榫頭/榫槽連接位置等應(yīng)力集中部位的載荷通常相對較高,易產(chǎn)生較大的蠕變變形和應(yīng)力松弛,從而對傳統(tǒng)疲勞壽命評(píng)價(jià)方法產(chǎn)生影響。準(zhǔn)確計(jì)算這些部位的蠕變變形及松弛應(yīng)力,是開展工程結(jié)構(gòu)件持久壽命[9-10]、蠕變疲勞交互影響[11-12]等研究的前提和基礎(chǔ)。同時(shí),由于缺口處的蠕變變形無法準(zhǔn)確測量,采用數(shù)值分析方法給出缺口蠕變變形特征也是一項(xiàng)重要的基礎(chǔ)研究。為此,作者基于ZSGH4169合金的蠕變數(shù)據(jù),采用16參數(shù)的θ-映射法模型對不同溫度、不同載荷下的蠕變曲線進(jìn)行分析,在獲得方程參數(shù)的同時(shí)考核模型的計(jì)算精度,并設(shè)計(jì)了具有不同應(yīng)力集中系數(shù)的缺口試樣,以凈截面應(yīng)力作為參考標(biāo)準(zhǔn),采用θ-映射法模型對其蠕變變形及應(yīng)力松弛行為進(jìn)行了模擬。
1 試驗(yàn)材料
試驗(yàn)材料為經(jīng)時(shí)效處理的GH4169合金鍛件,牌號(hào)記為ZSGH4169,其化學(xué)成分如表1所示[13]。
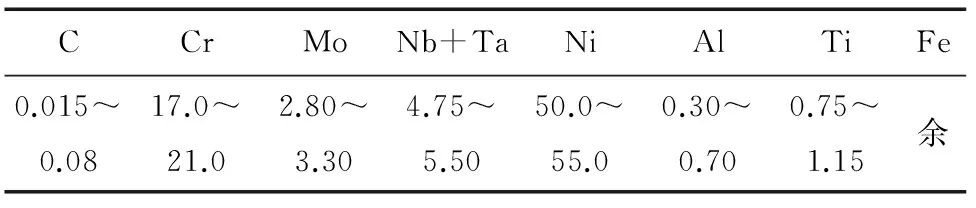
表1 ZSGH4169合金的化學(xué)成分(質(zhì)量分?jǐn)?shù))
試樣外輪廓尺寸為80 mm×18 mm×2 mm,工作段寬度為6 mm,與兩端銷釘夾持段以半徑為12 mm的圓角過渡,中部開單邊V型或雙邊半圓型缺口(圖1),缺口尺寸如表2所示。
缺口試樣應(yīng)力參數(shù)如表3所示。其中:σ0為計(jì)算應(yīng)力集中系數(shù)時(shí)的遠(yuǎn)端應(yīng)力;σn為缺口凈截面應(yīng)力,單邊缺口sn計(jì)算公式為s0/(1-DW),雙邊缺口sn計(jì)算公式為s0(1-2D/W),W為試樣寬度,D為缺口深度;σmax為缺口根部最大應(yīng)力,通過有限元計(jì)算獲得;Kt為應(yīng)力集中系數(shù),為最大應(yīng)力與靜截面應(yīng)力的比值。
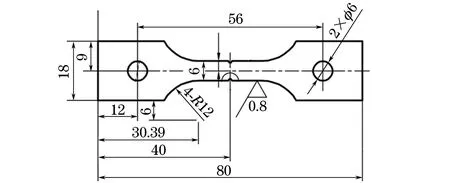
圖1 ZSGH4169缺口試樣的形狀與尺寸Fig.1 Shape and size of ZSGH4169 notched specimen
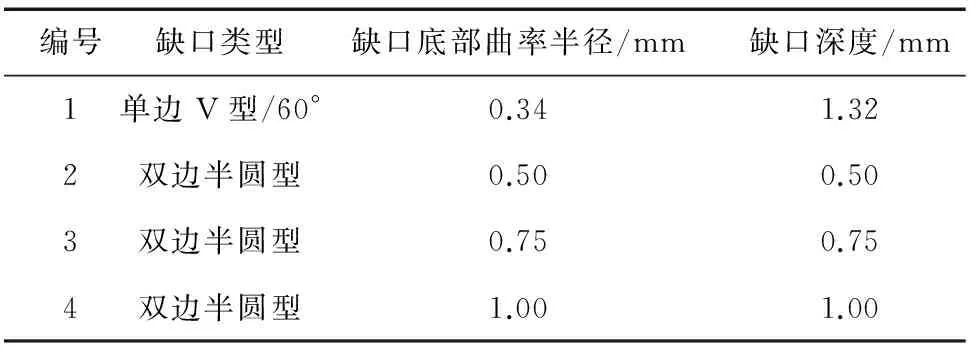
表2 缺口試樣的缺口類型與尺寸
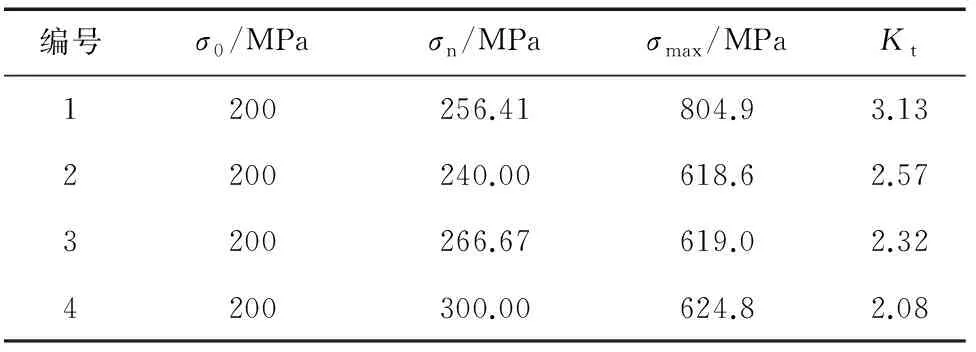
表3 缺口試樣的應(yīng)力參數(shù)
2 蠕變模型的建立
根據(jù)蠕變曲線特征,θ-映射法模型將蠕變過程假設(shè)為強(qiáng)化和弱化過程的疊加,蠕變速率恒定的第二階段可以看作是強(qiáng)化和弱化平衡的過程。基于此,能夠描述3階段蠕變曲線的方程為
εc=θ1[1-exp(-θ2t)]+θ3[exp(θ4t)-1]
(1)
式中:εc為蠕變應(yīng)變;t為蠕變時(shí)間;θi(i=1,2,3,4)為材料參數(shù)。
第一項(xiàng)描述了材料的硬化;第二項(xiàng)描述了材料的弱化;參數(shù)θ1和θ3描述了應(yīng)變的變化量;θ2和θ4描述了蠕變速率。
θi由應(yīng)力σ和溫度T決定,關(guān)系式為
lgθi=ai+biσ+ciT+diσT
(2)
式中:ai,bi,ci,di(i=1,2,3,4)為材料參數(shù)。
在模型建立過程中,應(yīng)力以材料在相應(yīng)溫度下的屈服強(qiáng)度作歸一化,溫度則以材料的熔點(diǎn)溫度作歸一化,這樣優(yōu)化得到的方程參數(shù)在數(shù)量級(jí)上不會(huì)相差過大,且計(jì)算過程中的蠕變變形數(shù)值更加穩(wěn)定。以ZSGH4169合金在650,700 ℃時(shí)不同應(yīng)力水平下的蠕變試驗(yàn)數(shù)據(jù)[13]為基礎(chǔ),將參數(shù)的獲取過程視為多參數(shù)優(yōu)化問題(共計(jì)16個(gè)參數(shù),與溫度、載荷以及時(shí)間相關(guān)),選擇Levenberg-Marquardt優(yōu)化算法,采用分步優(yōu)化策略[14]得到方程參數(shù),如表4所示。參數(shù)獲取過程是一個(gè)多參數(shù)優(yōu)化過程,不同優(yōu)化策略將獲得不同的結(jié)果,因此存在多組參數(shù)滿足要求,這里選擇1 組計(jì)算精度相對較高的參數(shù)進(jìn)行后續(xù)計(jì)算。
分別采用Fortran程序及MSC.MARC有限元程序?qū)SGH4169合金蠕變數(shù)據(jù)進(jìn)行模擬計(jì)算。Fortran程序的計(jì)算目的是實(shí)現(xiàn)θ-映射法,而有限元程序則是為工程結(jié)構(gòu)的蠕變分析服務(wù)。計(jì)算過程中,兩程序均采用表4中的參數(shù)。由圖2可以看出:采用Fortran程序的計(jì)算結(jié)果(空心點(diǎn))與有限元程序結(jié)合子程序(MSC.MARC)的計(jì)算結(jié)果(實(shí)線)完全吻合,說明程序編寫準(zhǔn)確;θ-映射法采用上述參數(shù)可較好地模擬出ZSGH4169合金在不同溫度、不種應(yīng)力下的蠕變變形行為,且能夠完整描述出蠕變各個(gè)階段的特征,特別是加速損傷的第三階段。
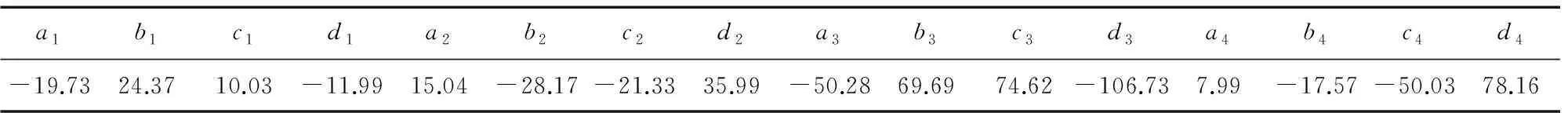
表4 ZSGH4169合金的θ-映射法模型參數(shù)
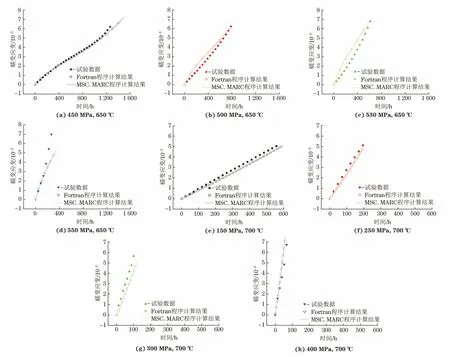
圖2 不同溫度及應(yīng)力下ZSGH4169合金蠕變試驗(yàn)結(jié)果與θ-映射法模型計(jì)算結(jié)果Fig.2 Creep test and θ-projection method calculation results of ZSGH4169 alloy under different temperatures and stresses
3 缺口試樣的蠕變變形模擬
3.1 蠕變變形計(jì)算方法
使用表4中θ-映射法模型參數(shù)計(jì)算各缺口試樣的蠕變變形,力邊界條件見表5。不同缺口試樣均以凈截面應(yīng)力作為對照標(biāo)準(zhǔn),應(yīng)力水平分別取300,375,450 MPa,結(jié)合5種應(yīng)力集中系數(shù)(包含Kt=1.00的情況,即無缺口試樣),進(jìn)行15種不同情況下的蠕變變形計(jì)算,蠕變計(jì)算時(shí)間取1 500 h。
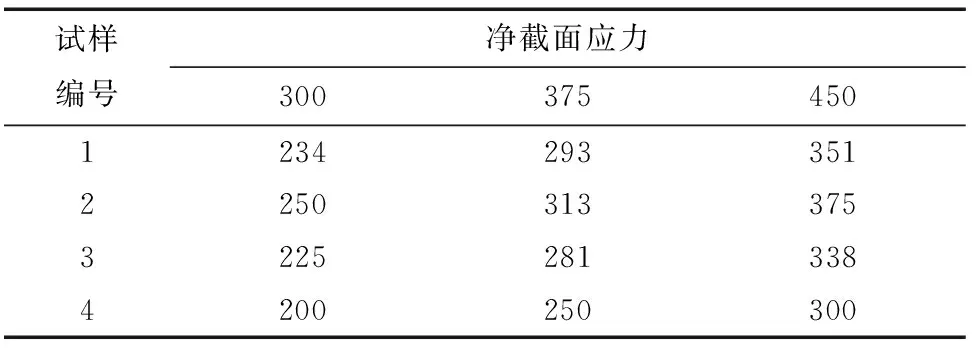
表5 缺口試樣在不同凈截面應(yīng)力下的遠(yuǎn)端應(yīng)力
3.2 V型缺口試樣的蠕變變形
對缺口有限元模型進(jìn)行網(wǎng)格劃分(圖3),重點(diǎn)分析沿缺口平分線向根部逐步深入的5個(gè)節(jié)點(diǎn)(編號(hào)為2328,2510,2509,2508,2507)的蠕變變化規(guī)律。由圖4可以看出,越靠近試樣缺口表面,V型缺口試樣(Kt=3.13)的蠕變應(yīng)變越大,應(yīng)力松弛越顯著。由于缺口位置為多軸狀態(tài),計(jì)算中給出的應(yīng)力均指等效應(yīng)力。拉伸方向(y方向)的應(yīng)力松弛在大小上略有不同。

圖3 V型缺口試樣有限元模型沿缺口根部平分線上的節(jié)點(diǎn)分布示意Fig.3 Schematic of nodes distribution of finite element model of V-notched specimen along symmetric path at notch root
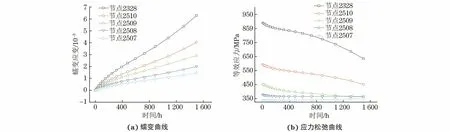
圖4 650 ℃、凈截面應(yīng)力300 MPa下V型缺口試樣不同節(jié)點(diǎn)的蠕變曲線及應(yīng)力松弛曲線模擬結(jié)果Fig.4 Simulation results of creep (a) and stress relaxation (b) curves of different nodes of V-notched specimen undernet section stress of 300 MPa at 650 ℃
由圖5可以看出:隨著凈截面應(yīng)力的提高,V型缺口試樣表面節(jié)點(diǎn)(編號(hào)為2328)的蠕變應(yīng)變增加;由于應(yīng)力提高使得高應(yīng)力區(qū)面積增加,試樣應(yīng)力松弛的時(shí)間較低應(yīng)力下的略有滯后。
3.3 不同缺口試樣的蠕變變形
由圖6可知,隨著應(yīng)力集中系數(shù)的增大,試樣蠕變變形程度增加,應(yīng)力松弛現(xiàn)象顯著。無缺口試樣(Kt=1.00)的蠕變應(yīng)變最小,該條件下應(yīng)力是恒定的,因此應(yīng)力松弛曲線中不包含Kt=1.00的情況。
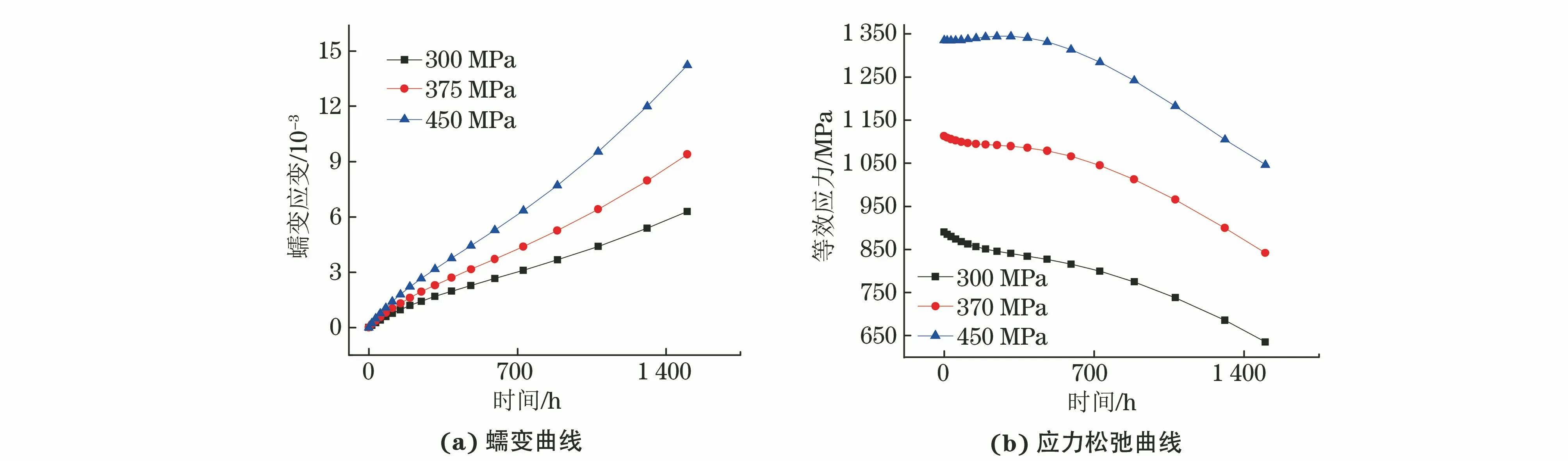
圖5 650 ℃、不同凈截面應(yīng)力下V型缺口試樣表面節(jié)點(diǎn)的蠕變曲線及應(yīng)力松弛曲線模擬結(jié)果Fig.5 Simulation results of creep (a) and stress relaxation (b) curves of surface node of V-notched specimen underdifferent net section stresses at 650 ℃
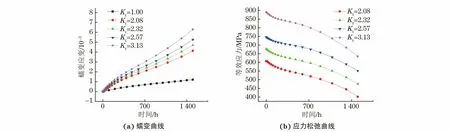
圖6 650 ℃、凈截面應(yīng)力300 MPa下不同缺口試樣表面節(jié)點(diǎn)的蠕變曲線及應(yīng)力松弛曲線模擬結(jié)果Fig.6 Simulation results of creep (a) and stress relaxation (b) curves of surface nodes of different notched specimens undernet section stress of 300 MPa at 650 ℃

圖7 650 ℃、凈截面應(yīng)力450 MPa下不同試樣表面節(jié)點(diǎn)的蠕變曲線及應(yīng)力松弛曲線模擬結(jié)果Fig.7 Simulation results of creep (a) and stress relaxation (b) curves of surface nodes of different notched specimens undernet section stress of 450 MPa at 650 ℃
由圖7可以看出,650 ℃、凈截面應(yīng)力為450 MPa時(shí),缺口試樣蠕變變形計(jì)算結(jié)果的變化趨勢與凈截面應(yīng)力300 MPa下的類似。應(yīng)力集中系數(shù)為2.08的缺口試樣的蠕變曲線計(jì)算結(jié)果與無缺口試樣的十分接近,這是由于其應(yīng)力集中程度及缺口應(yīng)力梯度不高,缺口根部曲率半徑與其他試樣的相比相對較大。上述分析說明根據(jù)不同載荷及試樣幾何特征,可以嘗試采用無缺口試樣來預(yù)測缺口試樣的蠕變變形。
對無缺口試樣和應(yīng)力集中系數(shù)為2.08的缺口試樣蠕變行為進(jìn)行進(jìn)一步分析。650 ℃、凈截面應(yīng)力為300 MPa下,t=0時(shí),缺口試樣表面節(jié)點(diǎn)的等效應(yīng)力為606.4 MPa,拉伸方向應(yīng)力為624.8 MPa;t=1 500 s時(shí),表面節(jié)點(diǎn)等效應(yīng)力為401.5MPa,拉伸方向應(yīng)力為418.6 MPa。以t=1 500 s時(shí)的應(yīng)力作為無缺口試樣(Kt=1.00)的拉伸應(yīng)力,以考察持續(xù)變載(應(yīng)力松弛)對蠕變變形的影響。由圖8可以看出,應(yīng)力松弛對蠕變變形計(jì)算結(jié)果產(chǎn)生了較大影響,相同恒定應(yīng)力條件下的蠕變應(yīng)變有所不同。
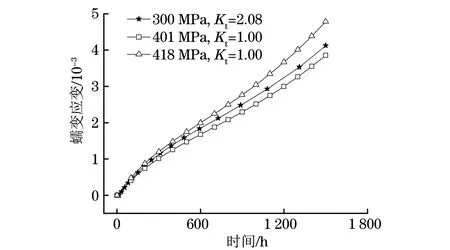
圖8 300 MPa凈截面應(yīng)力下缺口試樣及不同拉伸應(yīng)力下無缺口試樣的蠕變曲線計(jì)算結(jié)果Fig.8 Calculation results of creep curves of notched specimen under net section stress of 300 MPa and non-notched specimens under different tensile stresses
試驗(yàn)所建立的模型可以通過修正θ-映射公式來反映上述影響。缺口試樣的蠕變變形同應(yīng)力集中系數(shù)(與缺口凈截面應(yīng)力、表面最大應(yīng)力相關(guān))和應(yīng)力梯度(與缺口處幾何形式相關(guān))密切相關(guān),因此缺口處蠕變計(jì)算公式可表示為
εc=f(σ,T,t)·f(Kt)·f(dσ/dx)
(3)
式中:f(σ,T,t)為傳統(tǒng)蠕變模型;f(Kt)為針對應(yīng)力集中系數(shù)(或缺口根部最大應(yīng)力)的修正因子;f(dσ/dx)為針對應(yīng)力梯度的修正因子。
以上僅給出了描述缺口蠕變可能的表達(dá)式,對于具體表達(dá)式和可行的試驗(yàn)驗(yàn)證方法尚未進(jìn)行深入研究,且未對是否存在更好的優(yōu)化方法及流程,使計(jì)算結(jié)果的精度更高進(jìn)行探討,這將是重要的后續(xù)研究工作。
4 結(jié) 論
(1)θ-映射法模型可通過獲得的一組參數(shù)描述不同溫度、不同應(yīng)力下ZSGH4169合金的蠕變行為,計(jì)算精度較高,在提高計(jì)算效率的基礎(chǔ)上,能夠用于實(shí)際工程結(jié)構(gòu)的蠕變分析。
(2) 應(yīng)力集中程度越高,應(yīng)力梯度越大,ZSGH4169合金缺口根部的蠕變變形越明顯,應(yīng)力松弛程度越高;應(yīng)力集中系數(shù)較小、應(yīng)力梯度較為緩和時(shí),缺口根部的蠕變變形呈現(xiàn)與無缺口試樣相接近的趨勢。
(3) 引入應(yīng)力集中系數(shù)(或最大應(yīng)力)、應(yīng)力梯度影響因子對傳統(tǒng)蠕變模型進(jìn)行修正,給出了缺口試樣蠕變變形計(jì)算的一般表達(dá)式。

