白居塔塔體結構穩定性分析研究

張立乾，馮中華，陳 紅，閆 晶

（北京特種工程設計研究院，北京 100028）

0 引 言

白居寺，全國重點文物保護單位，位于西藏自治區日喀則地區江孜縣江孜鎮，南、北、東三面環山，海拔3 900 m，是一座藏傳佛教薩迦派、夏魯派、格魯派共存的寺院。白居寺始建于1427年，歷時10年竣工，是一座塔寺結合的典型的藏傳佛教寺院建筑，塔中有寺、寺中有塔，寺塔天然渾成，相得益彰，其建筑充分代表了13世紀末至15世紀中葉后藏地區寺院建筑的典型樣式。于2011年對白居寺中的吉祥多門塔（又稱為白居塔）的塔體建筑形制進行了充分調查，在此基礎上首次對白居塔體結構在重力和地震作用下的穩定性進行了深入研究，并合理推斷了白居塔體基礎和下伏山體的位置關系。白居塔整體形貌見圖1所示。

1 白居塔建筑形制

塔高分十層，總高41 m左右，底寬52 m左右，立面三角形。塔座為5個層級，塔身為圓形塔瓶，直徑20余米。依據白居塔建筑形制調查結果，白居塔平面布局圖見圖2所示，由內部筒狀墻體和內外部縱橫交錯布置的格構受力墻體系組成。白居塔墻體以泥砌塊石（片石）砌體結構為主，樓板為柔性木梁、檁條結構，屬于剛性墻體，柔性樓板結構。

圖1 白居塔俯瞰圖Fig.1 Overhead view of Baiju Tower

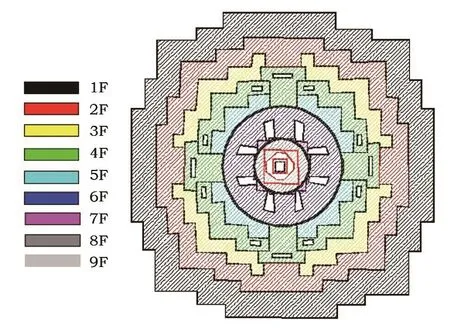
圖2 白居塔平面布局圖Fig.2 Plane layout of Baiju Tower

由于現場條件限制，建筑內部和山體的關系不能直接獲得，依據同類建筑形制進行推理，從布達拉宮到古格故城等城堡類建筑以及楚布寺多門塔和拉孜覺朗多門塔等塔式建筑都有依山而建的眾多先例，見圖3所示；另外從白居寺現場地形、地勢來看，其北側有一山體呈垂直切割狀，向南延伸恰好是白居寺所處的位置。基于以上分析，有理由推斷白居寺立面布局應依據山勢而建，其內部墻體建在環狀山包上。由于不能直接判斷內部嵌入山包的具體高度，依據北側山體現狀邊坡的自然坡率延伸至白居塔所處位置的坡體高度，分削坡和不削坡兩種情況，將內嵌山包分高（16 m，對應不削坡）、低（10 m，對應削坡）兩種情況進行探討。建筑立面布局圖4所示。

圖3 楚布寺多門塔立面與周邊環境Fig.3 Facade and surrounding environment of the auspicious multi-gate pagoda in Chubu Temple

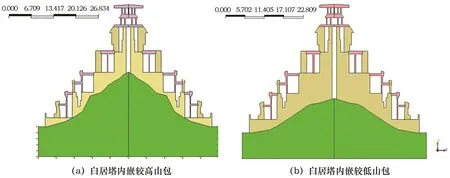
圖4 白居塔立面布圖Fig.4 Layout of Baiju Tower elevation

2 白居塔結構模型

2.1 物理力學指標

白居塔墻體為塊石砌體結構，樓板為木梁、檁條上覆阿嘎土結構。墻體、山體采用摩爾-庫倫本構模型，樓板采用彈性模型。模型的物理力學和結構指標見表1所示，表中圖例顏色與圖4中結構顏色相對應。

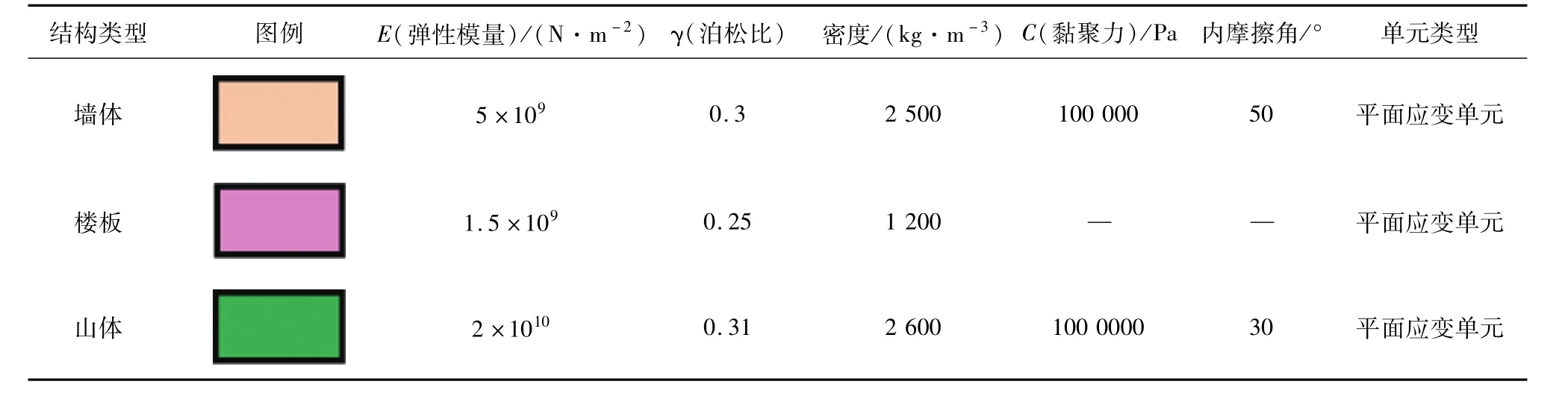
表1 物理力學參數表Table 1 Physical and mechanical parameters

墻體砌塊的物理力學指標體系中，砌塊的物理力學指標通過室內試驗和砌體回彈測試確定，砂漿則通過貫入測試獲得。通過砌塊和灰漿的物理力學參數，按照砌體強度理論推算出相應的砌體物理力學參數[1]。已知砌塊的抗壓強度平均值f1以及灰漿的抗壓強度平均值 f2，根據公式（1）（2）及（3）可得砌體的抗壓強度平均值fm、軸心抗拉強度平均值ft，m、彎曲抗拉強度平均值 ftm，m、抗剪強度平均值fv，m、彈性模量 E。 式中，ξ為彈性特征值。

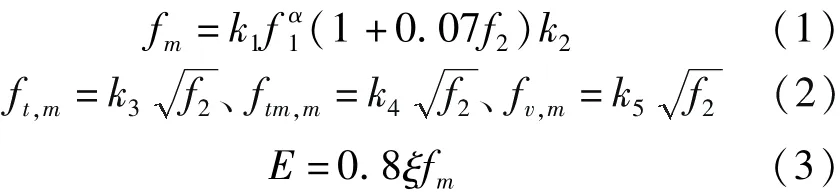
將砌體看成均質連續體，采用摩爾-庫侖模型進行計算。已知砌體的拉伸與壓縮強度參數，通過公式（4）及（5）計算得出砌體的黏聚力c及內摩擦角φ。

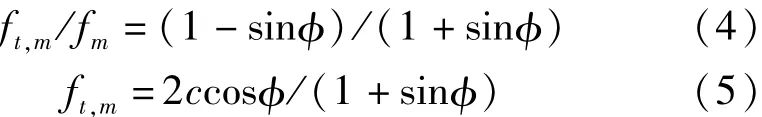
樓板物理參數取值依據規范《木結構設計規范：GB 50005—2017》[2]的參照值。山體物理參數取值依據《巖土工程勘察規范：GB 50021—2017》[3]、《建筑地基基礎設計規范：GB 50007—2011》[4]對應的中風化硬質巖的參照值。

2.2 安全穩定系數計算方法

采用強度折減法[5]計算結構體的安全穩定系數。有限元強度折減法分析結構體穩定性的基本思想是當計算正好收斂時（最小安全系數Ftrial再稍大一些，數量級一般為10-3，計算便不收斂），對應的Ftrial被稱為坡體的最小安全系數，此時土體達到臨界狀態，發生剪切破壞。強度折減法的基本公式見公式（6～8）。

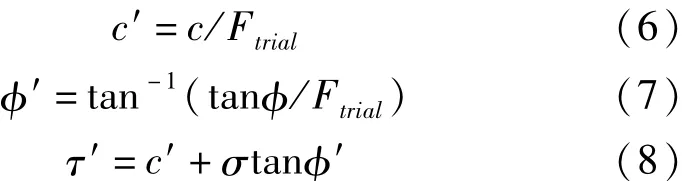
式中，τ為折減后的抗剪強度；σ為作用于巖土體上的正應力。

與傳統的條分法相比，抗剪強度折減系數法具有如下優點：1）能夠對具有復雜地貌、地質結構的邊坡進行計算；2）求解安全系數時，可以不假定滑移面的形狀，也無需進行條分；3）考慮了巖土體的本構關系以及變形對應力的影響；4）能夠模擬滑坡形成過程及其滑移面形狀（通常由剪應變增量或位移增量確定滑移面的形狀和位置）。

2.3 計算模型

采用midas GTS巖土分析軟件進行計算分析。依據《建筑抗震設計規范：GB 50011—2010》之3.4.4條之規定，對于平面或豎向不規則的建筑，應采取空間結構計算模型，考慮到塔體結構平面和豎向均規則，所以可以采取平面模型。塔體在三維空間上屬于軸對稱結構，通過軸心的垂向截面和水平向截面為結構寬度最小截面，可視為受力最不利截面。因此，作為塔體典型計算截面，按照平面應變問題，進行塔體穩定性計算分析。白居塔樓板木結構單元劃分大小為0.25 m，墻體單元劃分大小為0.35 m，山體單元劃分大小為1.2 m，單元總數量7 634個。邊界條件為：山體底部豎向和水平約束，山體側面水平約束，塔體底部與山體連接處為綁定連接。模型單元劃分見圖5所示。

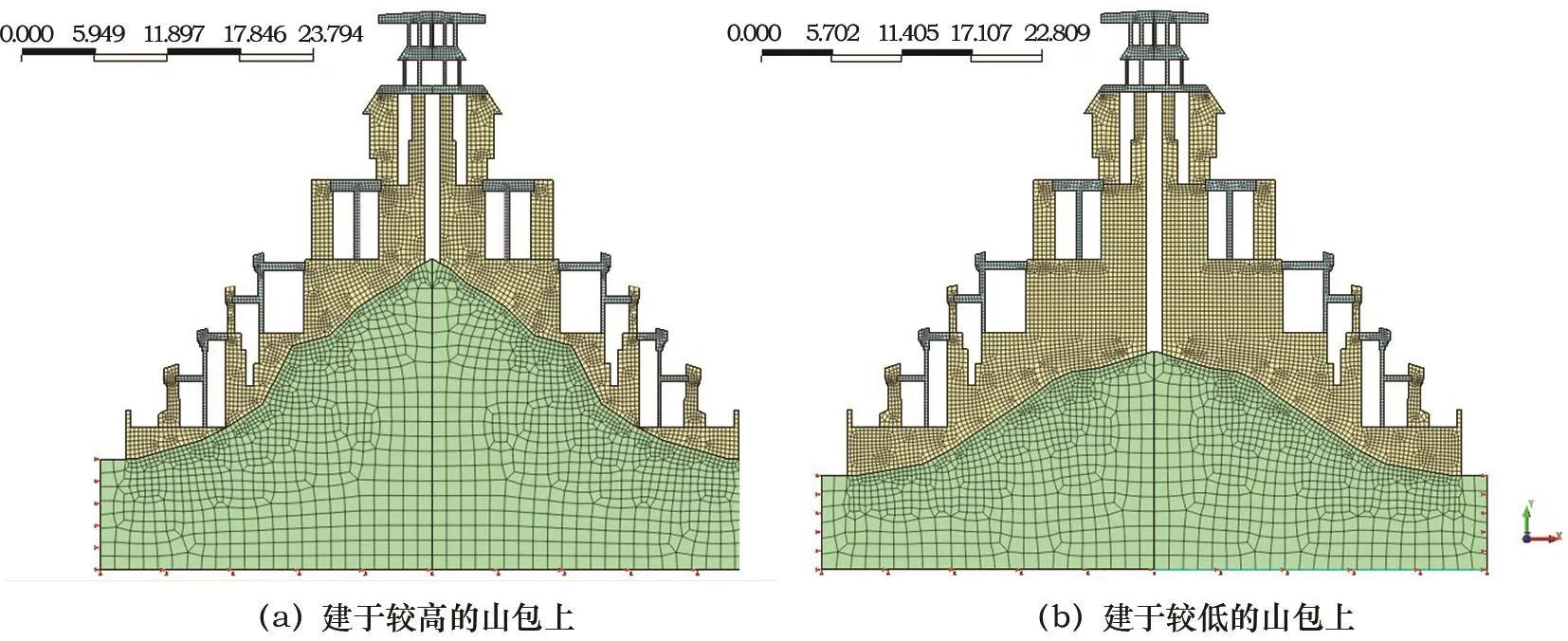
圖5 白居塔及山體有限元模型Fig.5 Finite element model of Baiju Tower and the mountain

3 重力作用下結構穩定性分析

塔體在自重作用下的結構位移圖見6所示，位移矢量圖見圖7所示，最大剪應變云圖見圖8所示。從圖6、圖7可以看出，較高山體模型在重力作用下，其最大變位為7.15 mm，結構的最大變位以6層墻體斜向下變位為主；較低山體模型在重力作用下，由于芯部墻體高達21 m，水平向剛度相對較弱，整體結構變位以向中心的水平變位為主，其最大變位為10.72 mm。

從圖8可以看出，較高山體模型在重力作用下，其最大剪切應變帶出現在7層平臺對應的內墻體下部，呈向下剪切模式。該部位控制整個結構的安全穩定系數，剪應變最大值為4 657με。較低山體模型在重力作用下，其最大剪切應變帶出現的位置不同，出現在7層平臺對應的內墻體下部，呈向下剪切模式。該部位同樣控制整個結構的安全穩定系數，剪應變最大值為6 356με。之所以出現剪切帶位置上的差異，原因在于墻體高的模型對應較高的臨空面，在豎向應力作用下，形成內下方剪切帶。

較高山體模型安全穩定系數為1.912 5，較低山體模型安全穩定系數為1.587 5。可見較高山體模型安全程度較較低山地模型高。兩個模型在自重作用下，整體的安全穩定均有較高的保證。

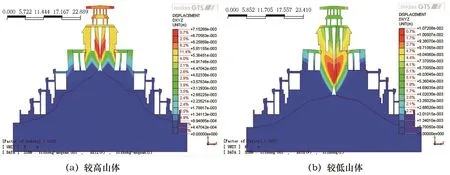
圖6 自重作用下變位圖（位移單位：m）Fig.6 Displacement diagram under the action of gravity（displacement unit： m）

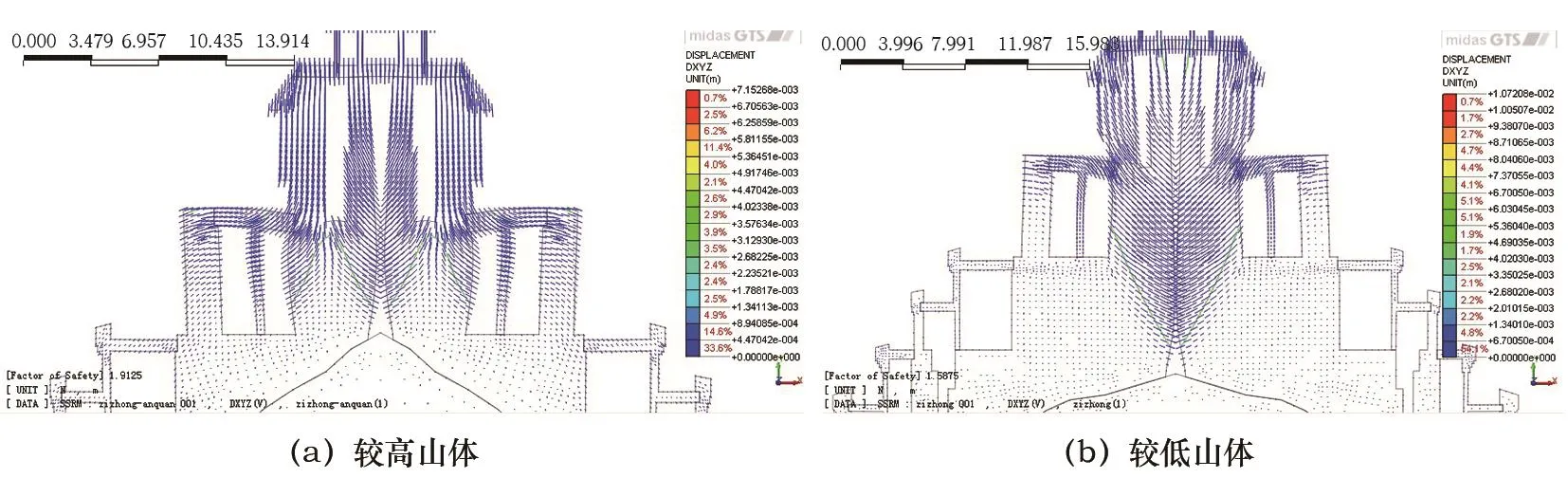
圖7 自重作用下變位矢量圖Fig.7 Vector diagram of displacement under the action of gravity

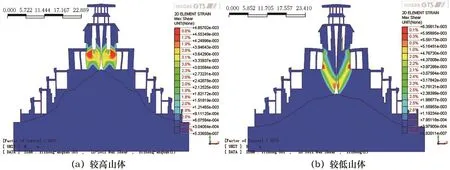
圖8 自重作用下最大剪應變云圖Fig.8 Maximum shear strain nephogram under the action of gravity

基于以上分析，在重力作用下，無論是較高山體模型，還是較低山體的模型，整體結構穩定性沒有問題，是安全的。

4 地震作用分析

白居塔主體結構以塊石砌體結構為主，樓板為柔性木梁、檁條結構，屬于剛性墻體，柔性樓板結構，采用底部剪力法計算較為合適。依據《建筑抗震設計規范：GB 50011—2001》[5]，該建筑位于西藏江孜，抗震設防烈度為7°，設計基本地震加速度為0.15 g，地震分組為第二組。7°設計基本地震加速度0.15 g時對應的水平地震影響系數為0.12（多遇地震），8°設計基本地震加速度0.3 g時對應的水平地震影響系數為0.24（多遇地震）。分別按照7°（對應設計基本地震加速度0.15 g）和提高一度8°（對應設計基本地震加速度0.3 g）選取水平地震系數0.12和0.24，用于該結構地震穩定性計算。

4.1 振型分析

分別針對較高山體和較低山體兩個模型進行模態分析，前4階振型見圖9、圖10所示，模態頻率表見表2所示。

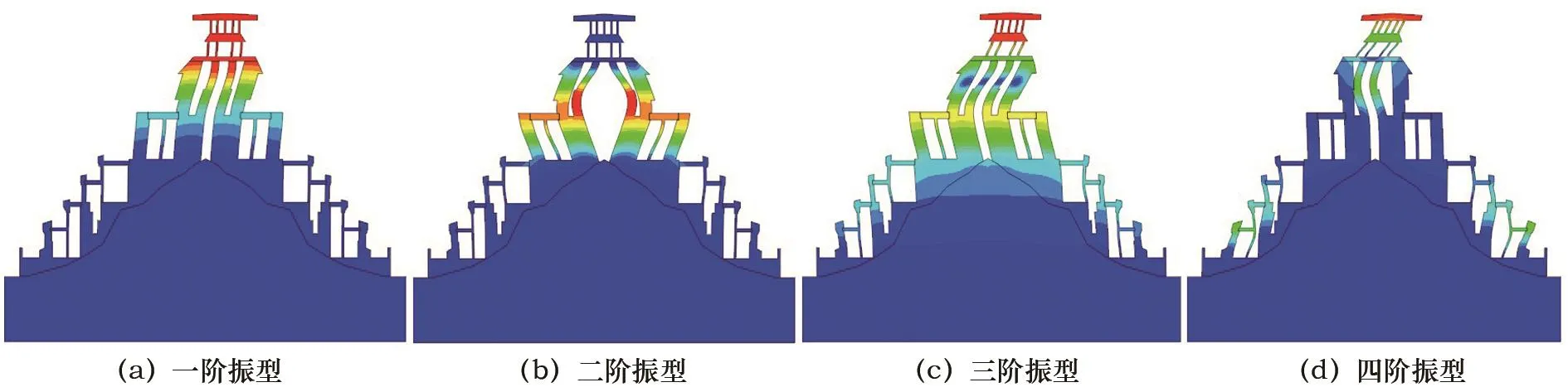
圖9 較高山體振型Fig.9 Vibration modes to higher mountain

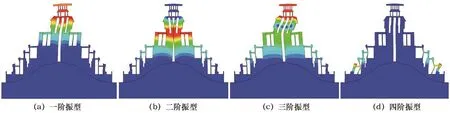
圖10 較低山體振型Fig.10 Vibration modes to lower mountain

表2 模態頻率表Table 2 Modal frequency

山體較高的模型，基頻為5.015 Hz，山體較低的模型，基頻為4.606 Hz，說明兩個模型結構整體剛度較大。兩個模型基頻形態均為上部側擺，山體較低模型側向剛度相對于山體較高模型為小。基頻形態為側向擺動，說明采取底部剪力法可用于該結構的抗震分析。兩個模型二階模態均為對稱擺動，三階模態均為扭擺，四階模態均為局部側擺，兩個模型的一致性較好。

4.2 7°多遇地震作用下結構穩定分析

從圖11可以看出，較高山體模型在重力和水平向多遇地震作用下，其最大變位為24.7 mm，結構的最大變位以6層墻體及以上水平向變位為主；較低山體模型在重力和水平向多遇地震作用下，左右側墻體變形雖均為側向水平變位為主，但左右側墻體分布并不相同，其最大變位為19.2 mm。

從圖12可以看出，較高山體模型在重力和水平向多遇地震作用下，其最大剪切應變帶出現在7層平臺對應的內墻體下部，呈向下剪切模式。該部位控制整個結構的安全穩定系數，剪應變最大值為5 938με，左右側墻體剪切形態基本一致。較低山體模型在重力作用下，其最大剪切應變帶出現的位置不同，出現在7層平臺對應的左側內墻體下部，呈向下剪切模式。該部位同樣控制整個結構的安全穩定系數，剪應變最大值為6 064με。而右側由于受壓為主，其剪切帶偏上，剪切應變較小，左右側剪切帶位置存有差異。原因在于墻體高的模型對應較高的臨空面，在豎向和水平向拉力的作用下，形成內下方剪切帶。

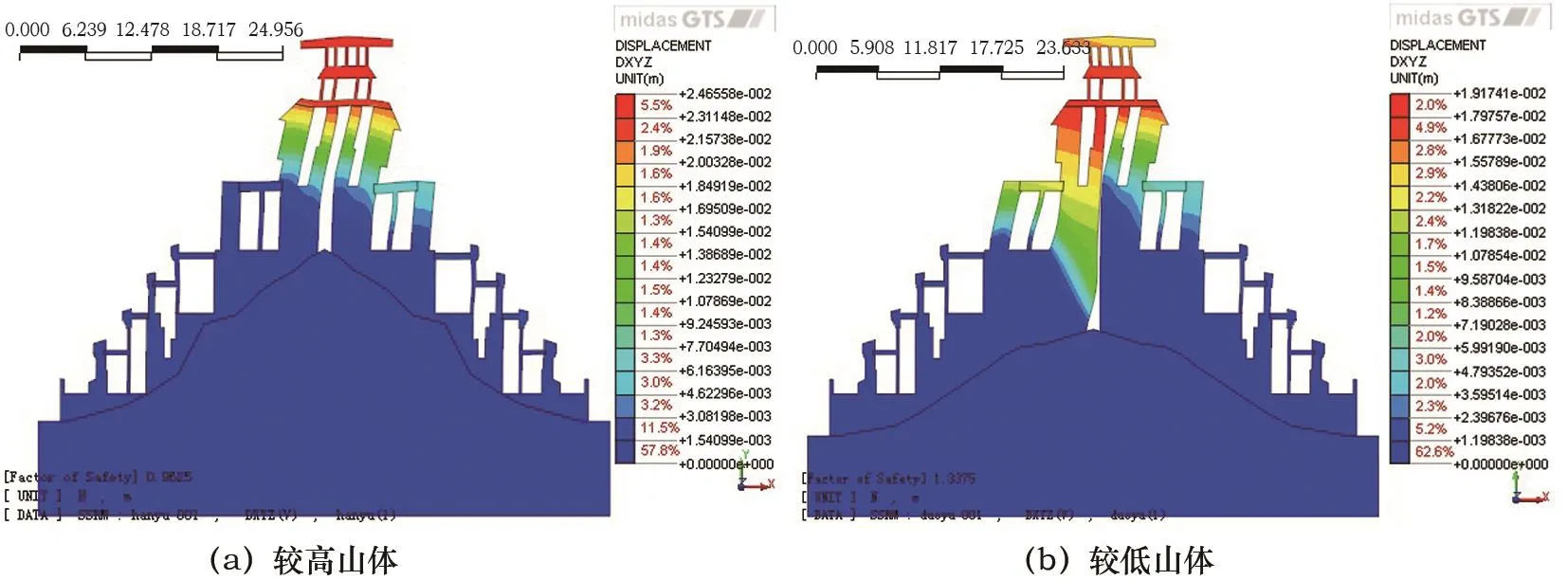
圖11 7°多遇地震作用下結構變位圖（位移單位：m）Fig.11 Structural displacement diagram under 7-degree frequent earthquakes（displacement unit： m）

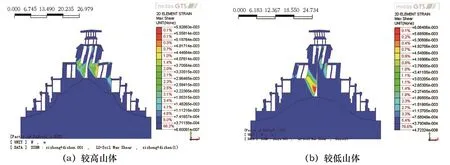
圖12 7°多遇地震作用下最大剪應變云圖Fig.12 Maximum shear strain nephogram under 7-degree frequent earthquakes

圖13 給出了自重和水平向多遇地震作用下結構的安全系數。較高山體模型安全穩定系數為1.637 5，較低山體模型安全穩定系數為1.337 5。可見較高山體模型安全程度較較低山地模型為高。兩個模型在自重和水平向多遇地震作用下，整體的安全穩定仍有較高的保證。

4.3 8°多遇地震作用下結構穩定分析

8°多遇地震作用下，由圖14可知，較高山體模型對應結構最大位移25.2 mm，較低山體模型對應結構最大位移為23.5 mm。由圖15可知，最大剪應變形態仍與7°多遇地震相同。由圖16可知，較高山體模型安全穩定系數為0.962 5，為安全穩定的臨界狀態；較低山體模型安全穩定系數為0.787 5，結構穩定系數不能滿足要求。

由模型參數表1可知，穩定系數的求解對應墻體C=100 kPa，φ=50°的本構模型參數。如果保持φ值不變，將C值增大20%，即取120 kPa，山體參數不變，再次計算兩個模型在8°多遇地震作用下的安全穩定系數。穩定系數計算結果見圖17所示。

圖13 7°多遇地震作用下結構安全穩定系數Fig.13 Safety and stability coefficients of structures under 7-degree frequent earthquakes

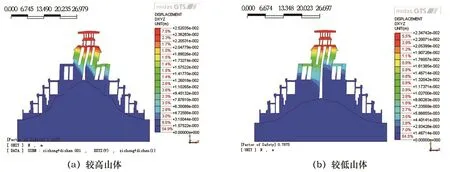
圖14 8°多遇地震作用下結構變位圖（位移單位：m）Fig.14 Structural displacement diagram under 8-degree frequent earthquakes（displacement unit： m）

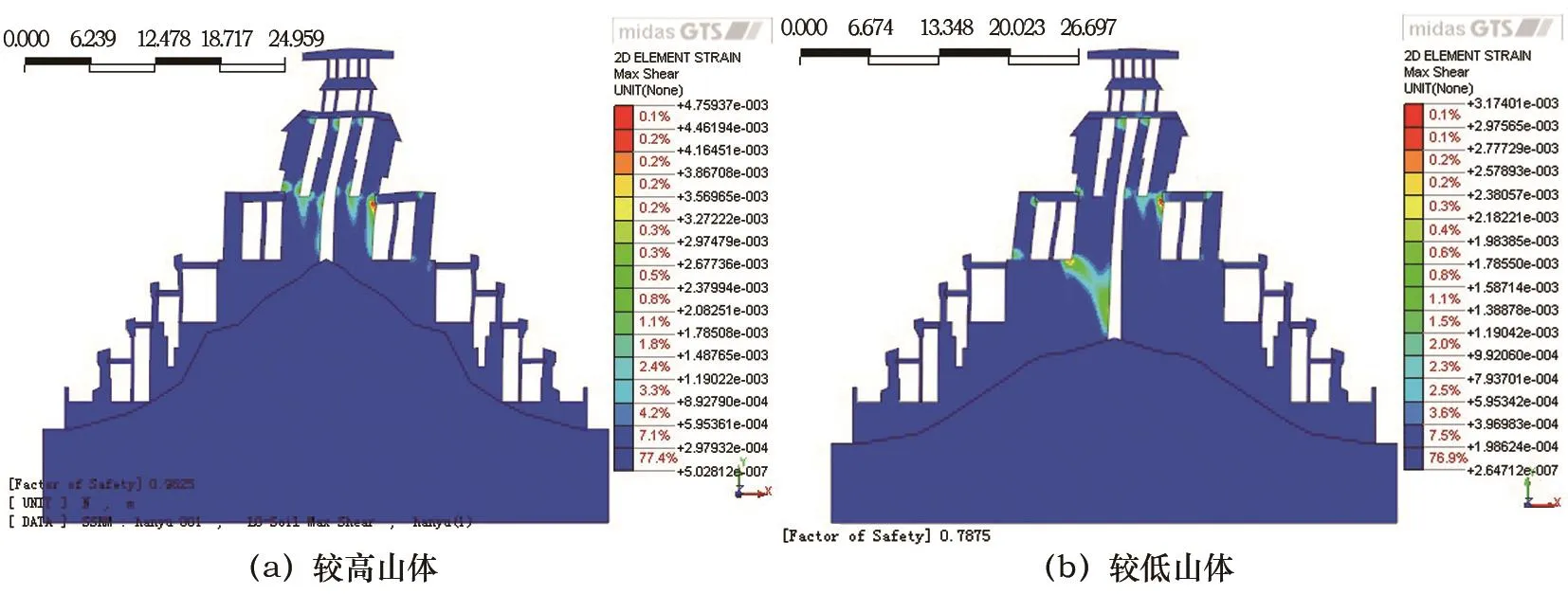
圖15 8°多遇地震作用下最大剪應變云圖Fig.15 Maximum shear strain nephogram under 8-degree frequent earthquakes

圖16 8°多遇地震作用下結構安全穩定系數Fig.16 Safety and stability coefficients of structures under 8-degree frequent earthquakes

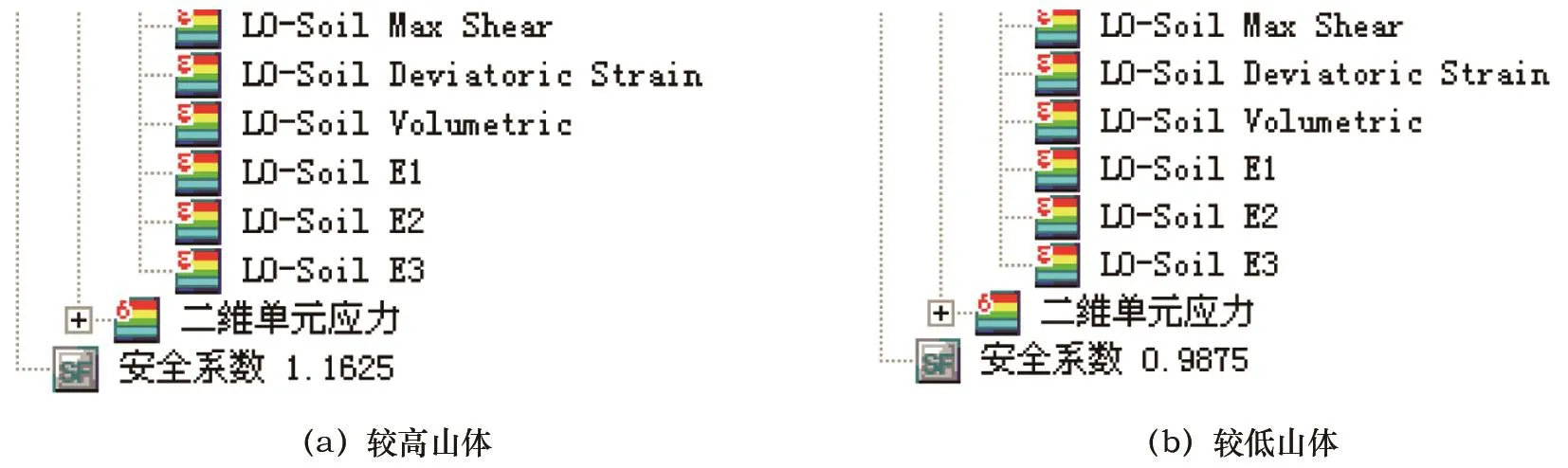
圖17 8°多遇地震作用下結構安全穩定系數Fig.17 Safety and stability coefficients of structures under 8-degree frequent earthquakes

由圖 14～17可知，C值增大 20%，即取120 kPa，其余參數不變，則較高山體模型穩定系數由0.962 5增至1.162 5，滿足大于1.1的要求。較低山體模型穩定系數也由0.787 5增至0.987 5。較高山體模型穩定性高于較低山體模型。C值的變化對結構穩定較為敏感。

對比而言，較高山體模型對應的安全穩定系數高于較低山體對應的安全穩定系數22%左右。結合白居塔經歷數百年風雨巋然不動的現實來推理判斷，白居塔真實可能的情況應該為塔體“內嵌”較高山體。

5 結 論

基于以上分析，對白居塔的整體穩定性可以得出如下結論：

1）無論較高山體，還是較低山體，白居塔整體結構的剛度較大，整個結構體系屬于抗震有利體系。

2）自重作用下，整體結構安全性滿足，且有較高的安全穩定系數。

3）白居塔整體結構基頻模態以側傾為主。在7°（基本加速度0.15 g）多遇地震作用下，兩個模型整體結構的抗震穩定性較好，結構不會產生整體性失穩破壞。在8°（基本加速度0.3 g）多遇地震作用下，較高山體模型主體結構基本處于安全臨界狀態，較低山體模型主體結構不滿足要求。較高山體的模型相對于較低山體的模型，安全程度要高。

4）分析模型采用了平面應變模型，未能考慮方形格構墻體中橫墻的抗剪作用。該部分會對結構產生有利的抗震作用，如果加以考慮，結構整體穩定系數會有一定程度的提高。

致 謝：謹以此篇文章獻給尊敬的我院已故文物保護工作開拓者楊國興先生。