近海鹽霧區鋼筋混凝土圓形截面構件承載力退化研究

谷音，李攀

(福州大學 土木工程學院，福州 350108)

鋼筋混凝土圓柱暴露在氯鹽環境中，氯離子通過混凝土基質滲透到鋼筋表面，使得鋼筋銹蝕，同時引起保護層混凝土開裂甚至剝落[1]，從而導致截面承載力出現退化。目前，腐蝕鋼筋混凝土截面剩余承載力評估方法已被很多學者關注。Akiyma等[2]通過OpenSees有限元模型，獲得了腐蝕矩形橋墩截面承載力曲線。Tapan等[3]考慮腐蝕導致的鋼筋和混凝土之間粘結能力退化，通過歐拉公式來評估銹蝕鋼筋的臨界受壓屈服應力，獲得不同腐蝕情況下鋼筋混凝土矩形截面軸力-彎矩相關曲線。Guo等[4]將矩形橋墩截面劃分為離散性纖維單元，進一步獲得氯鹽環境下鋼筋混凝土矩形柱在不同服役期的軸力-彎矩相關曲線。目前，不同腐蝕程度下混凝土柱矩形截面剩余承載力評估方法的研究已經相對完善。然而，已有文獻對圓形截面剩余承載力的研究較少。

為了確保混凝土圓柱在服役期的安全性，合理預測鋼筋混凝土圓柱開始腐蝕時間顯得尤為重要。Colepardi等[5]考慮擴散系數為常數，首次求解出氯離子在一維坐標下的擴散方程。Manget等[6]通過試驗發現氯離子擴散系數隨著時間增加而逐漸降低，可表達為時間函數，并對Colepardi等[5]提出的擴散模型進行更新。近年來，越來越多的學者開始考慮截面形狀對氯離子擴散的影響。Val等[7]采用有限差分方法對二維Fick擴散方程進行求解，獲得不同位置處鋼筋開始銹蝕時間。胡守旺等[8]采用有限元軟件(Comsol Multiphysis)模擬暴露氯鹽環境下不同服役期的預應力T梁中鋼筋表面氯離子濃度。Shafei等[9]通過利用有限元軟件模擬三維坐標下混凝土圓柱中鋼筋開始腐蝕時間。相比復雜的計算方法及有限元建模，簡潔的數學模型更方便且更有效地預測氯離子在混凝土中擴散。對于混凝土圓柱，Morga等[10]考慮擴散系數為常值，采用變量分離方法對極坐標下Fick二維擴散方程進行求解，獲得了圓形擴散模型。Song等[11]指出，隨著混凝土水化作用持續發生，毛細孔率逐漸降低，擴散系數隨著服役時間增長而改變。通過對6座不同齡期普通硅酸鹽混凝土的擴散系數實測數據進行回歸分析，Pack等[12]驗證了擴散系數強烈依賴服役時間。汪加梁等[13]考慮擴散系數為時變函數，對圓形擴散模型進行了更新。Morga等[10]與汪加梁等[13]研究結果表明，對于混凝土圓柱，混凝土表面氯離子濃度值越小，圓形截面半徑對鋼筋開始腐蝕時間的影響越明顯。McGee等[14]根據對位于Tasmania的1 158座橋梁的研究，結果表明，混凝土表面氯離子濃度隨著離海岸線距離增加而逐漸降低。Akiyma等[15]也指出空氣中氯離子濃度隨著海岸線距離顯著降低。由此可見，隨著海岸線距離增加，混凝土圓柱形狀對評估鋼筋開始腐蝕的影響越顯著。

筆者研究了不同海岸線距離混凝土圓形截面形狀對評估鋼筋開始腐蝕時間的影響，進一步分析了形狀對評估截面承載能力退化率的影響，給出了更加合理評估鋼筋混凝土圓柱承載力退化率的建議。

1 鋼筋混凝土圓柱開始腐蝕時間

1.1 氯離子擴散模型

假設混凝土基質為均勻材料，氯離子在圓形截面中擴散可采用極坐標下Fick第二定律來描述，如式(1)所示。

(1)

式中：D為氯離子擴散系數；t為擴散時間；C(ρ,t)為距離圓心ρ處t時刻的氯離子濃度；考慮氯離子擴散系數為時間t的函數，如式(2)所示[6]。

(2)

式中：m為混凝土老化系數，m=2.5(w/c)-0.6，其中，w/c為水灰比；Dref為養護齡期tref對應的氯離子擴散系數，一般tref取28 d，D28可表達為D28=10-12.06+2.4(w/c)[16]。

氯離子在圓形截面擴散中滿足如下假定：1)表面氯離子濃度為常值；2)截面中氯離子濃度分布滿足軸向對稱；3)混凝土基質中初始氯離子濃度為0。

對C(ρ,t)采用分離變量C(ρ,t)=φ(ρ)ψ(t)，結合式(2)，式(1)可更新為

(3)

對式(3)進行變形

(4)

式(4)中，等號左側僅為變量t的函數，右側僅為ρ的函數。當且僅當左右兩邊的方程等于相同常數λ2時，等式(4)成立。式(4)可變形為

(5)

對方程組(5)中等式分別求解，基于氯離子在混凝土圓形截面擴散假設，氯離子在圓形截面中的擴散模型可更新為

Ccir(ρ,t)=

(6)

式中：C0為混凝土暴露在環境中的表面氯離子濃度；R為混凝土圓柱半徑；J0為零階貝塞爾函數；J1為一階貝塞爾函數；αn是方程J0(Rαn)=0的根。

若忽視圓形截面對氯離子擴散的影響，評估鋼筋表面氯離子濃度時，平板擴散模型如式(7)所示[6]。

(7)

式中：x為保護層厚度；erf為高斯誤差函數。

為了對比平板擴散模型與圓形擴散模型，文獻[17]定義了Ccir(R-x,t)/Cslab(x,t)，其中R為圓形截面半徑，分析了表面氯離子濃度C0、擴散系數D28、老化系數m、保護層厚度x、半徑R、擴散時間t參數對Ccir(R-x,t)/Cslab(x,t)比值的影響。通過參數分析結果，圓形擴散模型可被簡化為修正平板擴散模型，如式(8)所示。

Ccir(x,t)=(1.8R-1.3x+1)·

(8)

平板擴散模型評估開始腐蝕時間Tslab，表達式為

(9)

式中：erf-1為高斯誤差反函數；Ccr為氯離子濃度閾值；C0為混凝土表面氯離子濃度。

考慮圓形截面對開始腐蝕時間的影響，通過修正平板擴散模型評估開始腐蝕時間，表達式為

(10)

1.2 開始腐蝕時間計算

為了提高結構的使用耐久性，《混凝土結構耐久性設計與施工指南》(CCES 01-2004)[18]對暴露在近海鹽霧區混凝土結構構造做出了具體規定。當距離海岸線0.1 km內時，為重度鹽霧區，混凝土柱的最大設計水灰比為0.36，最小保護層厚度為55 mm；當距離海岸線0.1 km外至0.3 km內時，為輕度鹽霧區，最大設計水灰比為0.4，最小保護層厚度為50 mm。

考慮鋼筋混凝土結構處于最易遭受氯離子腐蝕狀態，保護層厚度取最小設計值，水灰比取最大設計值。待確定參數表面氯離子濃度與濃度閾值具有較大隨機性。為了簡化分析，其參數取具有一般水平的均值。根據文獻[19]，氯離子腐蝕的濃度閾值的均值為0.9 kg/m3，混凝土表面氯離子濃度均值為海岸線距離dcoast函數，如式(11)所示。

(11)

研究半徑為40、60、80、100 cm的鋼筋混凝土柱。通過式(9)與式(10)分別評估不同dcoast下腐蝕開始時間，結果如圖1所示。當dcoast超過0.1 km時，鋼筋開始腐蝕時間隨著海岸線距離顯著增加。修正平板擴散方程與平板擴散方程評估開始腐蝕時間的差值如圖2所示。當混凝土圓柱暴露在輕度鹽霧區時，開始腐蝕時間差值保持恒定且小于5 a，當dcoast大于0.1 km時，該差值逐漸增加。圖2中不同dcoast所對應的開始腐蝕時間差值見表1。

圖1 海岸線距離dcoast所對應的鋼筋腐蝕開始時間TiFig.1 The time to corrosion initiation of RC circular column corresponding to dcoast

圖2 采用修正平板擴散方程與平板擴散方程所產生的開始腐蝕時間差值ΔTiFig.2 The difference value between the time to corrosion initiation estimated by modified slab diffusion model and this time estimated by original slab one

表1 不同半徑下dcoast所對應的開始腐蝕時間差值(ΔTi/a)Table 1 The difference of the time to corrosion initiation corresponding to dcoast at a series of radius

2 腐蝕鋼筋混凝土圓柱截面承載力模型

2.1 材料性能退化模型

Du等[20]提出了腐蝕鋼筋屈服強度退化模型，如式(12)所示。

fy(t)=(1-0.5η(t))fy0

(12)

式中：fy(t)為腐蝕時間t鋼筋剩余屈服強度；fy0為未腐蝕鋼筋屈服強度；η(t)為t時刻鋼筋質量損失率。

自然環境下腐蝕鋼筋主要以點蝕形態存在，如圖3所示。若鋼筋腐蝕形態沿長度方向保持一致，η(t)可采用截面積損失率表示。

(13)

式中：D0為正常鋼筋直徑；As(t)為鋼筋剩余面積，計算模型如式(14)～式(18)所示[21]。

(14)

(15)

(16)

(17)

(18)

式中：p(t)為t時刻局部銹蝕深度，根據文獻[22]，具體表達式為

(19)

(20)

式中：R為局部腐蝕系數，均值為7.1。

圖3 鋼筋剩余面積計算示意圖Fig.3 Schematic diagram of resiudal corroded area bar

銹蝕產物的體積膨脹，導致保護層混凝土開裂甚至剝落。Qi等[23]結合理論與試驗結果，提出鋼筋腐蝕量與保護層混凝土開裂寬度的半經驗與半理論模型，如式(21)～式(23)所示。

Wc=Wc1+Wc2

(21)

(22)

(23)

式中：Wc為單位長度鋼筋腐蝕量；γ為鐵的密度，取為7.85 mg/mm3；ρ為體積膨脹系數，取值為3；c為保護層厚度；d為鋼筋直徑；w為保護層混凝土裂縫寬度；當混凝土E為混凝土彈性模量；fc為混凝土28 d抗壓強度；α0、β0、α1、β1為修正系數。

當鋼筋開始腐蝕后，保護層混凝土開裂寬度所對應的Wc與腐蝕開裂時間Tcr滿足

Wc=γp(Tcr)

(24)

式中：V為鋼筋腐蝕速率；p(Tcr)為開裂時間Tcr所對應的局部腐蝕深度。

當保護層混凝土開裂嚴重時，腐蝕速率增加，如式(25)所示[24]。

λ2(t)=(4.5-26λ1(t))λ1(t)

(25)

保護層混凝土剝落后，式(12)不再適用于評估腐蝕鋼筋抗壓強度。此時腐蝕鋼筋臨界受壓屈服應力為[3]

(26)

式中：Es為腐蝕鋼筋彈性模量，腐蝕對彈模的影響可以忽略；Is(t)為t時刻腐蝕鋼筋截面慣性矩；Lexp為鋼筋暴露長度。

由于Coronelli等[25]提出的保護層混凝土抗壓強度退化模型不適用于圓形截面，當保護層混凝土未剝落時，假定保護層混凝土抗壓強度不變。根據文獻[26]，當裂縫寬度到達極限值1 mm時，裂縫擴展嚴重，可認為保護層剝落，其抗壓強度為零。考慮箍筋腐蝕對于約束混凝土的影響，在已知箍筋的剩余面積和屈服強度后，通過Mander模型來計算約束混凝土的抗壓強度。

2.2 截面承載力計算公式

如圖4所示，保護層混凝土采用拋物線本構，保護層混凝土峰值應力對應的應變為0.002，極限應變為0.003 3。考慮鋼筋為理想彈塑性材料，采用雙線性本構描述應力-應變關系。核心混凝土采用Mander模型計算應力-應變關系，細節見參考文獻[27]。

圖4 材料應力-應變關系Fig.4 The relationship between the stress and strain of material

對于腐蝕后圓形混凝土截面，仍滿足平行截面假定。圖5中，εcu為保護層混凝土極限壓應變；xc為混凝土截面受壓高度；εsc與εst為鋼筋壓應變與拉應變。混凝土劃分成若干個水平層狀單元，每根鋼筋作為單獨單元處理。σco(i)為i單元處保護層混凝土抗壓強度，σcc(i)為i單元處核心混凝土抗壓強度，σsc(j)為j位置處鋼筋抗壓強度，σst(k)為k位置處鋼筋抗壓強度。當圓形截面劃分條帶層數量較多時，每個不規則水平層狀條帶簡化為矩形單元，如圖6所示。對于每個混凝土矩形單元，所提供的軸力Nc(i)與彎矩Mc(i)可表示為

(27)

(28)

Nc(i)=Nco(i)+Ncc(i)

(29)

Mc(i)=(R-id)N(i)

(30)

若劃分混凝土條帶層狀單元不包含核心混凝土時，Ncc(i)變為0，Nco(i)重新表達為

(31)

整個圓形截面軸力和彎矩的平衡條件為

(32)

(33)

式中：p為混凝土條帶層狀單元數量；m為截面受壓鋼筋數量；n為截面受拉鋼筋數量。

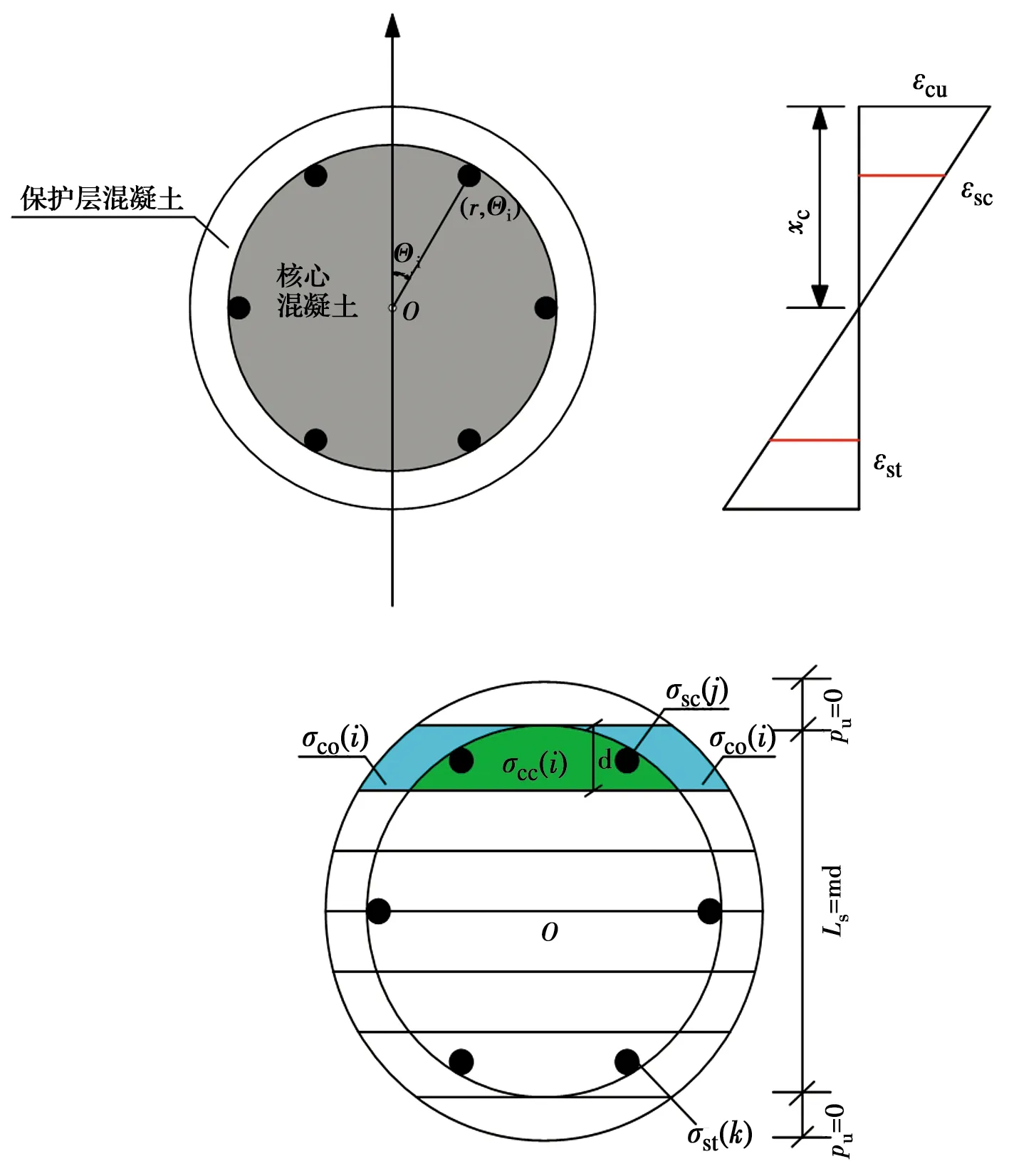
圖5 鋼筋混凝土圓形截面應變-應力分布及條帶層劃分Fig.5 The strain-stress distribution and layer element division of circular section of reinforced concrete

圖6 第i個混凝土條帶層示意圖Fig.6 Schematic diagram of the ith concrete layer element

基于Matlab，編制混凝土圓柱截面彎矩承載力計算程序。給定截面軸向荷載Np，通過圖7所示流程可得截面彎矩承載力。

圖7 計算指定軸力下截面彎矩承載力示意圖Fig.7 Flow chart of calculating bending moment capacityunder specified axial force at circular across-section

2.3 模型驗證

《混凝土結構設計規范》(GB 50010—2010)[28]對正常圓形截面承載力計算公式進行了詳細描述。若鋼筋腐蝕率為0，即鋼筋未發生腐蝕的情況，將規范與筆者所提出的計算方法進行對比。假定鋼筋混凝土圓柱截面半徑為60 cm，保護層厚度為5 cm，截面配置24@25 mm、設計屈服強度為360 MPa的縱筋。箍筋采用直徑為10 mm、間距為80 mm的HPB300，設計屈服強度為270 MPa。混凝土抗壓強度分別取30、40、50 MPa。計算結果如圖8所示。需指出的是，筆者考慮了截面處于軸心受壓狀態。在軸力-彎矩相關曲線中，彎矩為零對應為截面所能承受的最大軸力值。在彎矩為零附近未考慮水平直線段。

圖8 規范(GB50010-2010)與本文計算模型對比Fig.8 Comparison between Code (GB50010-2010) and calculation method proposed in the paper

由圖8可見，當豎向軸力較小時，采用的計算方法與規范計算結果吻合很好。當軸力增加時，混凝土受壓高度增加，所對應的彎矩承載力大于規范計算值，這是由于規范中未考慮箍筋對核心的約束作用，核心混凝土強度取值與保護層混凝土強度一致。對比結果表明，計算方法對未腐蝕性圓形截面同樣適用，一定程度上反映了腐蝕圓形截面承載力計算方法的合理性。

Ma等[29]設計了13個不同腐蝕程度的混凝土圓形柱來研究墩柱的力學性能退化規律。選取其中5個發生彎曲破壞的圓形橋墩試驗信息進行對比。縱筋實測屈服強度為373.2 MPa，箍筋實測屈服強度為327 MPa，28 d混凝土實測抗壓強度為32.4 MPa，加載高度為0.82 m。朱杰[30]對不同腐蝕程度的鋼筋混凝土圓柱進行擬靜力試驗，構件均發生彎曲破壞。縱筋實測屈服強度為355.626 MPa，箍筋實測屈服強度為230.677 MPa，28 d混凝土實測抗壓強度為30.43 MPa。加載高度為1.1 m，以上試驗構件中的鋼筋質量損失率與軸壓比信息分別列于表2和表3中，試驗樣本的截面及配筋信息如圖9所示。Ma等[29]試驗信息中，未對箍筋腐蝕率進行描述。參考已有文獻[31-32]試驗結果，取箍筋腐蝕率為縱筋腐蝕率的2倍。

圖9 試驗樣本構造圖(單位:mm)Fig.9 The detail of experiment specimen (unit: mm)

表2 Ma等試驗樣本腐蝕率和軸壓比信息Table 2 The specimens about corrosion degree and ratio of axial compression stress to strength by Ma et al

表3 朱杰試驗樣本腐蝕率和軸壓比Table 3 The specimens about corrosion degree and ratio of axial compression stress to strength by Zhu

由于鋼筋的不均勻腐蝕，試驗樣本的骨架曲線往往出現不對稱現象。需指出的是，Ma等[29]試驗資料中未給出正負加載方向的承載力信息。給出的承載力試驗值為構件正負加載方向的均值。預測值與試驗值的比值分布如圖10(a)所示。朱杰[30]試驗資料中，給出了構件正負加載時各自承載力試驗值。預測值與正向承載力比值如圖10(b)所示，預測值與負向承載力比值如圖10(c)所示。通過統計分析，試驗與預測比值分布的均值為0.88，方差為0.07。由此可見，預測值略低于試驗值。在加速腐蝕過程中，縱筋的截面損失率沿墩高并非一致。保護層混凝土考慮完全剝落，受壓鋼筋采用歐拉公式即式(26)計算得到。實際情況中，保護層混凝土具有分布裂縫而并非完全脫落。這些原因導致預測值與試驗值的比值分布具有較大離散性，且普遍小于1。文獻[4]將腐蝕鋼筋混凝土矩形截面承載力預測值與試驗結果進行對比，結果表明了相同現象。考慮腐蝕截面的安全富余，該模型可作為圓形截面的剩余承載力評估。圖10中的數據信息匯總見表4。

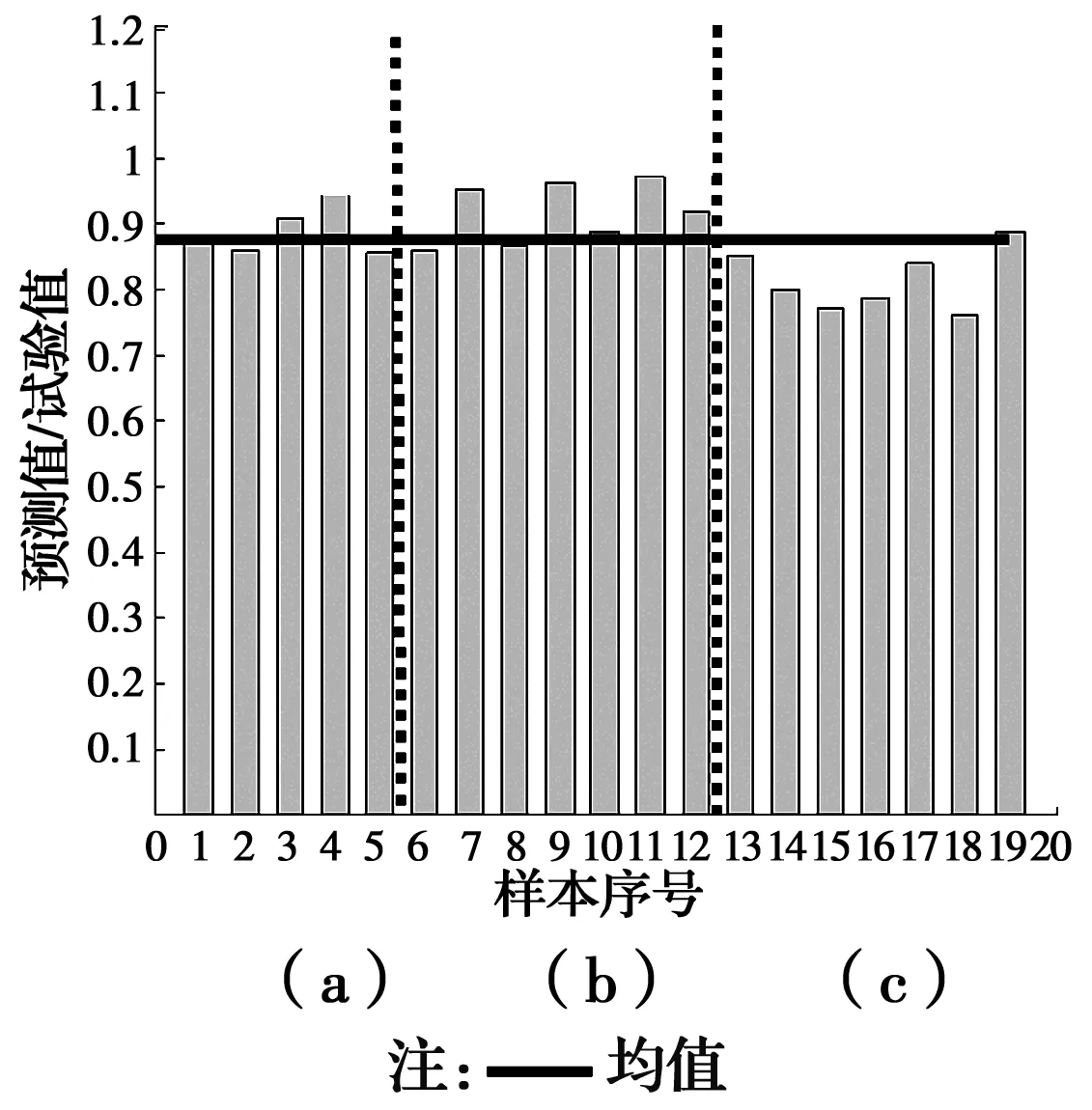
圖10 預測值與試驗值比值分布Fig 10 The distribution of the ratio of predicted value and experiment value

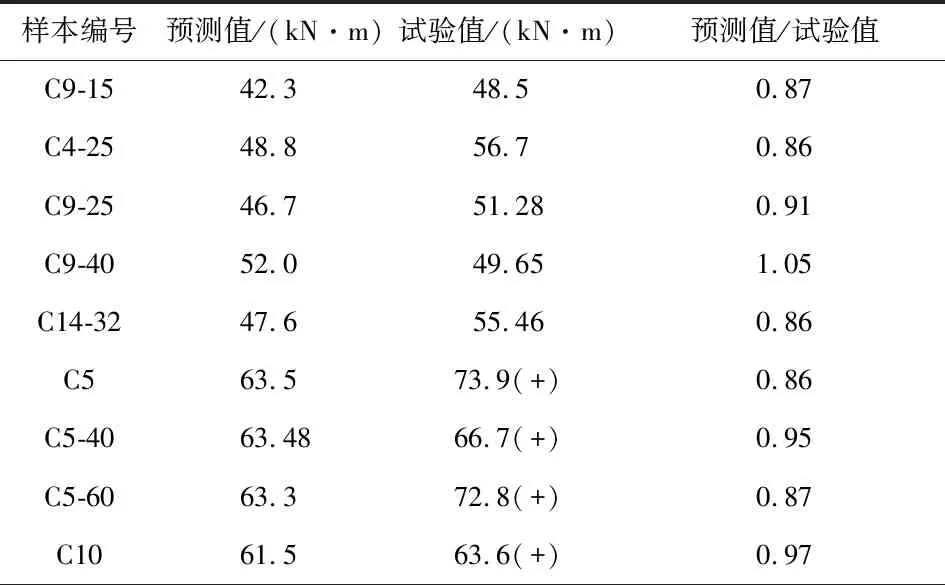
表4 試驗樣本的預測值與試驗結果對比Table 4 Comparison between predicted value and experimental value of specimens

續表4

3 算例分析

以半徑為40、60、80 cm的鋼筋混凝土圓柱為研究對象，柱高4 m，采用C40混凝土，設計抗壓強度為19.1 MPa，水灰比為0.4。混凝土保護層厚度為50 mm。當半徑為40 cm時，配置12@25 mm的HRB400縱向鋼筋，半徑分別為60、80 cm時，截面分別配置24@25 mm與44@25 mm的HRB400縱向鋼筋，縱筋設計屈服強度為360 MPa。箍筋采用直徑為10 mm、間距為80 mm的HPB300，設計屈服強度為270 MPa。通過式(21)～式(24)可得，鋼筋開始腐蝕后，保護層混凝土剝落時間為3.6 a。不同銹蝕時間Tc下圓形截面時變軸力-彎矩相關曲線如圖11所示。

圖11 鋼筋銹蝕時間對截面N-M曲線影響Fig.11 The effect of corrosion time on N-M curve of RC circular column

由圖11可見，當保護層混凝土剝落時，截面承載力出現驟降。選取截面最大軸向承載力Nmax，最大彎矩承載力Mmax以及截面軸力為零對應的彎矩承載力M0作為研究對象。基于圖11中數據，Nmax、Mmax及Nmax在不同腐蝕時間時所對應的退化率如圖12。由圖12可見，對于M0，不同銹蝕時間下，各半徑所對應的退化率基本保持一致。然而，對于Mmax和Nmax，半徑越小，相同銹蝕時間所對應的退化率越高。對比M0、Mmax和Nmax，截面M0退化程度最為顯著，其次為Mmax。這是由于截面受壓高度越大，半徑越大，鋼筋對承載力的貢獻越小，腐蝕對截面承載的影響越小。從擬合方程可見，退化率與銹蝕時間很好地滿足了線性關系，且不同半徑下，退化率隨銹蝕時間增長速率基本相同。

由圖2和圖12可見，采用平板擴散模型將高估鋼筋開始腐蝕時間，從而低估截面承載力的退化率。由于M0的退化程度最為明顯，通過圖12(a)中的擬合方程，不同海岸線距離下所對應的M0退化率差值如圖13所示。從圖13可以看出，對于重度鹽霧區，各半徑所對應的退化率差值均小于4%。隨著海岸線距離增加，退化率差值逐漸增加，采用平板擴散模型對評估承載力退化率的影響逐漸增加。對于輕度鹽霧區，圖12中不同半徑所對應的退化率差值見表5。由表5可見，當半徑為40 cm時，退化率差值的均值為6.6%。當半徑增加為60 cm時，差值降低到4.2%。

圖12 鋼筋銹蝕時間對M0、Mmax、Nmax的退化率影響Fig.12 The effect of corrosion time on the degradation rate of M0、Mmax、Nmax

圖13 截面M0退化率差值隨海岸線距離變化圖Fig.13 The difference value of bearing capacity M0 degradation rate varying with dcoast

表5 不同海岸線距離dcoast下M0退化率差值Table 5 The difference of M0 degradation rate under a series of dcoast

4 結論

推導與驗證了腐蝕鋼筋混凝土圓形截面承載力計算模型。考慮近海鹽霧區截面形狀對鋼筋開始腐蝕時間的影響，對比了分別采用修正平板擴散模型與平板擴散模型對評估鋼筋混凝土圓柱截面承載力退化率的影響，得到如下結論：

1)采用平板擴散模型將高估近海鹽霧區鋼筋混凝土圓截面中鋼筋開始腐蝕時間。海岸線距離越大、半徑越小，高估現象越明顯。

2)保護層混凝土剝落，使得截面承載力出現急劇下降。鋼筋銹蝕對軸力為0所對應的彎矩承載力M0的影響最為明顯。隨著半徑增大，鋼筋腐蝕對截面承載力的影響逐漸減小。

3)鋼筋混凝土圓柱在重度鹽霧區時，采用平板擴散模型所引起的截面承載力退化率差值小于4%，可以直接采用平板擴散模型評估鋼筋開始腐蝕時間。位于輕度鹽霧區時，當半徑為40 cm，該承載力退化率差值的均值為7%，當半徑為60 cm，該差值的均值變為5%左右。為了控制差值在5%以內，當鋼筋混凝土圓柱半徑小于等于60 cm且暴露在輕度鹽霧區時，建議使用修正平板擴散方程評估圓柱鋼筋腐蝕開始時間，進一步評估截面剩余承載力。