超混沌耦合發電機系統的混沌控制
謝艷云 蔡文良
(1.2.重慶水利電力職業技術學院,重慶 永川 402160)
自1990 年Pecora 等提出的混沌控制和混沌同步以來,混沌的研究已成為科學界的熱點之一,許多學者已廣泛關注對混沌和超混沌系統的控制研究,文獻[3]采用比例微分控制器實現了非自治系統和自治系統的混沌控制;文獻[4]進一步提出一類嚴格反饋型非線性系統的變比例增益的混沌控制;文獻[6]采用微分反饋控制法和控制法消除了一個新非線性系統的混沌現象,文獻[7]采用單變量脈沖控制法實現了超混沌的控制。
本文在文獻[8-9]的基礎上,對四維超混沌耦合發電機系統 的超混沌控制問題進行了研究,分別采用控制和比例微分控制兩種超混沌控制法消除了系統中的超混沌現象,對比這兩種控制方法,受控后系統的動力學行為有明顯的區別,為該系統在工程上的實施提供理論依據,也為其他系統的超混沌控制提供了經驗。
一、四維超混沌耦合發電機系統模型
文獻[8]在三維耦合發電機系統的基礎上增加一個非線性控制器,構成了一個新的四維超混沌耦合發電機系統,該方程的狀態方程表示為:
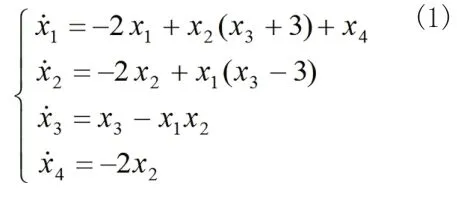
文獻[9]對上述四維超混沌耦合發電機系統(1)進行了詳細的動力學分析,采用MATLAB 軟件,利用四階龍格-庫塔方法對系統(1)進行數值仿真,選取初始點發現系統(1)于超混沌運動狀態,圖1 為系統的吸引子在X1-X2面上的投影圖。
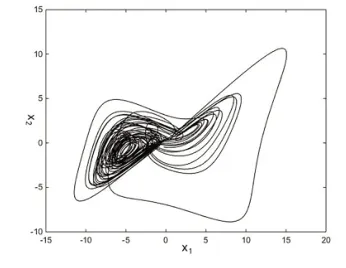
圖1 系統(1)的吸引子圖
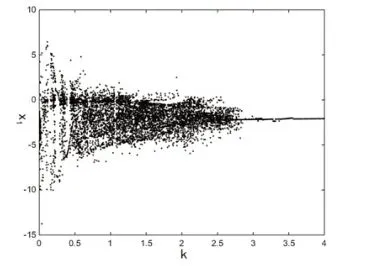
圖2 施加控制后系統(2)的分岔圖
在耦合發電機系統(1)中的第一個方程加入負反饋控制器,其中變量為k反饋增益,就可以得到受控系統的為:
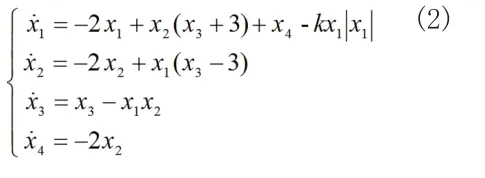
這樣只要稍微改變受控系統中的反饋增益就可以將耦合發電機系統(1)中的超混沌運動控制到周期運動。數值仿真采用MATLAB 軟件和四階Runge-Kutta方法,得到受控系統(2)關于K 的全局分岔圖,如圖2 所示,從圖2 可以看出,隨著反饋增益的增大,受控系統(2)可以穩定到周期軌道。選取反饋增益K=3.5 時,可以將受控系統(2)穩定到周期一軌道,圖3 為受控系統(2)穩定到周期一軌道的吸引子在X1-X2和X1-X4面上的投影圖.
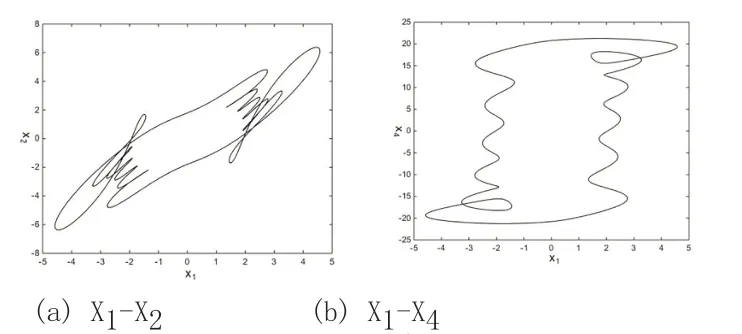
圖3 施加控制后系統(2)的吸引子圖
三、比例微分控制
現選取耦合發電機系統(1)中的狀態變量為X2受控變量,取比例微分得:
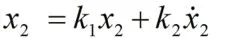
其中K1和K2是比例微分控制方法中的兩個可調參數,可以通過調整K1和K2這兩個參數的值來實現超混沌控制.現將耦合發電機系統(1)按如下方式進行反饋
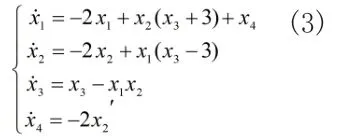
為了方便討論,不失一般性,令K1=1,對于實施反饋后的系統(3),通過數值仿真,采用MATLAB 軟件,選取不同的K2,可以使實施反饋后的系統(3)穩定到周期軌道。當時K2=1.81 時,可將實施反饋后的系統(3)穩定到單周期軌道,其吸引子在X1-X2、X1-X3、X1-X2-X3和面上的投影圖如圖4 所示。
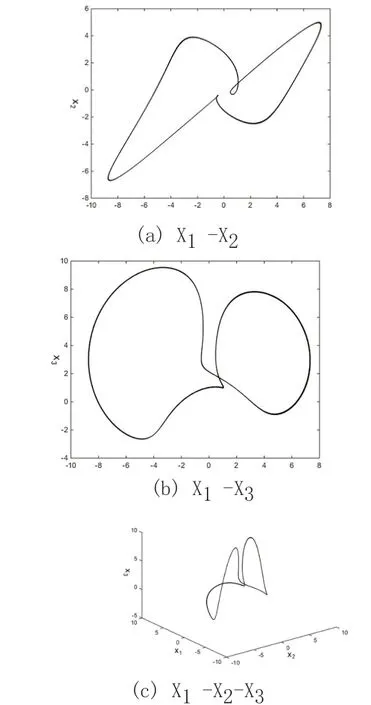
圖4 系統(3)的相圖
四、結論
基于四維超混沌耦合發電機系統模型,采用了兩種超混沌控制方法,選取合適的反饋增益和比例微分參數,能有效的使四維超混沌耦合發電機系統穩定到周期軌道,同時通過數值模擬驗證,驗證了這兩種超混沌控制方法的有效性,且為該系統的在實際工程應用中提供理論依據。

