基于RFM及線性回歸的商場會員活躍度研究

田 恬 高汝林 鄭春華 劉 楠 呂海俠

(陜西工業職業技術學院 陜西 咸陽 712000)

引言

在零售行業中，會員是銷售額和利潤的主要貢獻者。但電商產業的迅猛發展使傳統零售業受到沖擊，商場許多會員失活，造成巨大損失；并且發展新會員的資金投入又太高。因此，如何激活會員，讓更多的非活躍會員變為活躍會員，就成為商場決策者關注的主要問題，也是零售運營商制定策略的主要參考依據。

基于此，本文以2018年全國大學生數學建模競賽專科組C題[1]的附件數據為基礎，對會員消費行為進行分析。構建了基于RFM[2]的會員消費狀態分類模型，將會員分為活躍會員和非活躍會員；建立了激活率與促銷系數的回歸模型，揭示了非活躍會員激活率與商場促銷活動呈線性關系，為傳統零售運營商決策者激活失活會員提供重要依據。

一、基于RFM的會員消費狀態分類模型

會員的狀態和激活非活躍會員是本文需要解決的問題。在此之前，必須選擇合適的時間窗口。考慮到在時間窗口內購買行為必須具備延續性和穩定性，對原始數據經過預處理后[3]，得到2015年1月—2018年1月商場每月的會員購物次數，如下圖1。

圖1 商場每月會員購物次數

由圖1可知，2015年8月—2016年1月會員幾乎沒有在商場購物，因此2015年1月—2016年1月這段時間不適合選為時間窗口；又考慮到商場一般以年(或12個月)為單位處理會員狀態或積分，因此本文選取2017年1月—2017年12月為時間窗口。

結合相關文獻[4-5]以及實際生活經歷可知，會員活躍度是可以通過會員購物行為體現的。長時間不購物，活躍度就會下降；而頻繁的購物，活躍度就顯著提升。因此，認為會員在時間窗口消費時間越連續、消費頻次越高，會員狀態越活躍。本文選取RFM模型中的‘R’最近一次消費時間和‘F’消費頻率作為對會員狀態進行劃分的依據。通過最后一次消費時間(R)描述會員消費時間的連續性；消費頻率(F)描述會員購物總頻次。構造如下RF會員消費狀態分類模型。

X(i)=Rt(i)*Ft(i)

(1-a)

Rt(i)=f(Ri)，Ft(i)=φ(Fi)

(1-b)

這里的Rt(i)和Ft(i)分別代表會員i以R、F為分類依據的相應變量評分。Rt(i)在1～2之間變化，Ft(i)在1～3之間變化，兩個指標相乘得到消費狀態X(i)的變化區間為1～6，評分越高，說明會員越活躍。本文定義X(i)在1～3之間會員狀態為非活躍，在4～6之間為活躍。

其中Rt(i)和Ft(i)的評分標準如下：

①Rt(i)的構建

若會員的R處于時間窗口的首月(即1月)，則Rt(i)=2，否則Rt(i)=1；若R處于時間窗口的次月至末月(即2-12月)，會員上個月也發生購買，則Rt(i)=2，否則Rt(i)=1。即會員最后購物時間越連續，Rt(i)越大，會員越活躍。

②Ft(i)的構建

(2-a)

(2-b)

其中Fi(j)表示會員i在第j個月是否發生消費，若消費，則為1，否則為0。Fi表示時間窗口內消費月頻次(Fi可隨具體的時間窗口變化，如時間窗口是一個月的話，Fi表示消費周頻次)，特別的，若Fi=0，即整年沒有一次消費，則為僵尸會員，則將該會員當作非會員處理。當會員消費時間越持續，Ft(i)就會越大，則會員越活躍。

本文對選取的商場會員消費數據進行處理，利用消費狀態分類模型得到2017年不同狀態的會員數據如表1所示。

表1 2017年不同狀態的會員數及對應比例

由表1可知，非活躍會員和活躍會員對應占比分別為95%和5%，說明會員群體中絕大多數處于不活躍狀態，活躍會員較少。由此可見，開展針對性的營銷策略，引導非活躍會員消費，轉為活躍會員，刻不容緩。本文針對一點，繼續探索。

二、激活率與促銷系數回歸模型

(一)激活率——狀態轉移概率矩陣模型

本節欲研究非活躍會員激活率，并試圖探究其與商場活動的內在機理。故先對商場會員狀態變化概率進行研究。

在上節的基礎上，建立消費人員狀態轉移概率矩陣[6]，表示會員狀態的動態變化。現有商場消費人員狀態可分為三大類：活躍會員、非活躍會員和非會員。其中非活躍會員轉變為活躍會員的概率，就是非活躍會員的激活率。

統計出時間段ti內的非會員、活躍會員和非活躍會員的總量Pi、Ii和Ni，同理可以得到時間段ti+1內的Pi+1、Ii+1和Ni+1。建立如下的狀態轉移概率矩陣模型：

Si+1=Ti,i+1Si

(3-a)

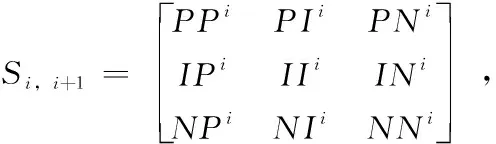
(3-b)

(3-c)

其中，Si,i+1表示三種狀態相互轉化的狀態轉移概率矩陣；NIi表示由時間段ti變為ti+1時，非活躍會員轉為活躍會員的概率，即非活躍會員激活率(Si,i+1中的其他8個元素意義類似，表示由前一狀態轉變為后一狀態的概率值)。

針對上述狀態轉移概率矩陣模型，繼續選取2017年消費數據(以每月為一時間窗口)，共計12個時間段，計算出11組激活率，結果如下表2所示。

表2 2017年1月至2017年12月每月會員激活率

由表2可知，會員在1月的激活率最高，為0.32，這說明有近3成的非活躍會員在2月份轉變成活躍會員，這與春節正好處于2月份吻合；7-8月的激活率都保持較高水平，這與暑假時間相吻合；9月的激活率最低，僅為0.049，這可能是因為現在“旅游熱”，會員10月轉為活躍的可能性就會減少。除了這些外在因素，思考非會員激活背后的原因，本文認為，這與商場是否促銷，促銷程度大小有一定的關系。

(二)基于激活率與促銷系數的線性回歸模型

本文將商場促銷力度簡化為會員消費金額與對應商品總標價的比值，即在同一時間段ti內，αi表示商場的促銷系數，公式如下，

(4)

其中，Costi表示時間段ti內會員總消費金額；Pricei表示時間段ti內會員消費商品總標價。αi=1表示商場無促銷，αi<1表示商場有促銷活動。且促銷程度越大，αi越小。

經計算可以得到2017年1月到2017年12月的激活率與促銷系數，并畫出散點圖，結果如圖2所示。

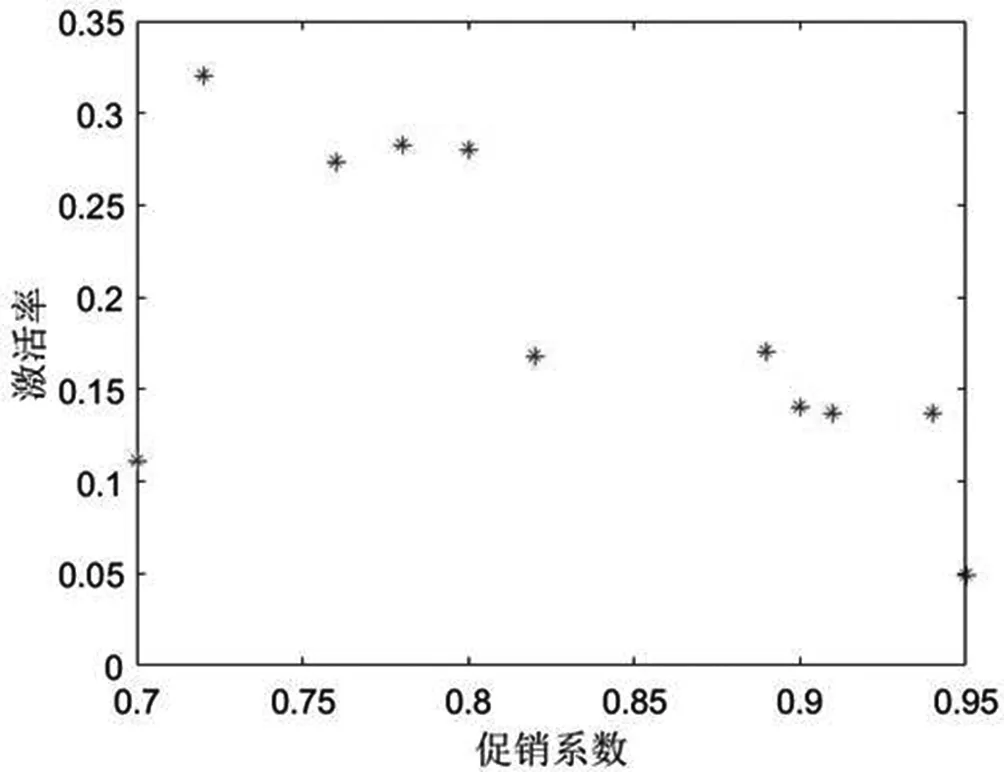
圖2 激活率與促銷系數散點圖

觀察散點圖，可以看出激活率與促銷系數基本呈線性關系，因此，可以建立如下的激活率與促銷系數的線性回歸模型[7]，

NIi=b0+b1αi+ε

(5)

利用上述模型對激活率與促銷活動進行線性回歸擬合，剔除異常數據后的擬合曲線如下圖3。

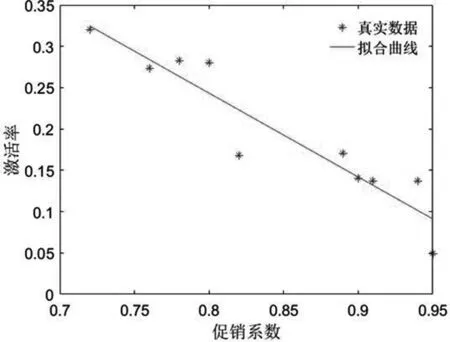
圖3 擬合曲線

擬合曲線為：

NIi=1.0555-1.0151αi，R2=0.88

(6)

圖3表明，擬合效果良好。并且可以看出，隨著促銷活動力度的加大(αi減小)，非活躍會員的激活率也在逐漸增加。因此，商場管理可以利用打折等促銷活動來激活非活躍會員，為商場帶來更多利潤。

三、小結

本文從某大型百貨商場的消費數據出發，構建了基于RFM的會員消費狀態分類模型，對商場會員評分，最終將商場會員分為2類:非活躍會員和活躍會員，發現非活躍會員比例高達95%，與現實情況相符；通過觀察激活率與促銷系數的散點圖，發現激活率與促銷系數呈線性關系，最終建立了激活率與促銷系數的線性回歸模型。為決策者激活失活會員提供重要依據。