基于BP神經(jīng)網(wǎng)絡(luò)模型的住宅用地地價(jià)評(píng)估研究
——以南昌市主城區(qū)為例

陳志鵬，郭 熙，趙麗紅*，郭細(xì)根

(1.江西農(nóng)業(yè)大學(xué)國(guó)土資源與環(huán)境學(xué)院，330045，南昌；2.重慶理工大學(xué)經(jīng)濟(jì)金融學(xué)院，400054，重慶)

0 引言

改革開放以來，我國(guó)土地交易市場(chǎng)的建設(shè)取得重大突破。從土地公開市場(chǎng)的土地出讓收益來看：1999—2015年，這17 a全國(guó)土地出讓收入總額為37 457億元，2017年這一數(shù)據(jù)猛增至52 059億元[1]。由此可見，我國(guó)土地出讓市場(chǎng)呈現(xiàn)異常活躍、交易量大的特點(diǎn)。為了規(guī)范土地交易市場(chǎng)，抑制土地價(jià)格的不合理增長(zhǎng)，對(duì)土地估價(jià)的精度要求也越來越高，提高地價(jià)評(píng)估的客觀性和科學(xué)性很有必要。在此背景下很多學(xué)者基于不同視覺、采用不同的技術(shù)方法對(duì)地價(jià)評(píng)估進(jìn)行研究，如回歸模型[2]、模糊數(shù)學(xué)[3]、云模型[4]、克里金插值[5]等方法。但上述方法均未考慮地價(jià)影響因素權(quán)值確定這一主觀性問題。隨著人工智能的興起，不少學(xué)者將人工智能方法運(yùn)用于地價(jià)評(píng)估，如BP神經(jīng)網(wǎng)絡(luò)，支持向量機(jī)[6]和隨機(jī)森林[7]等方法。該些方法均規(guī)避了地價(jià)影響因素的權(quán)重問題，建立地價(jià)與其影響因素間的映射關(guān)系，更具有一定的客觀性與優(yōu)越性。

與傳統(tǒng)估價(jià)方法中的市場(chǎng)比較法相比，BP神經(jīng)網(wǎng)絡(luò)有很多相似之處，但是與市場(chǎng)比較法不同的是，神經(jīng)網(wǎng)絡(luò)不需要人為地確定修正系數(shù)，這也就在很大程度上降低了人為因素對(duì)估價(jià)的影響。因此為減少在土地估價(jià)過程中人為主觀性，提高估價(jià)科學(xué)性，本文將BP神經(jīng)網(wǎng)絡(luò)引入到住宅地價(jià)評(píng)估中，采集南昌市主城區(qū)100多個(gè)住宅土地交易案例，探討適用于南昌市主城區(qū)住宅用地的地價(jià)評(píng)估自動(dòng)機(jī)制。

1 基于BP神經(jīng)網(wǎng)絡(luò)模型算法的地價(jià)評(píng)估模型

1.1 BP神經(jīng)網(wǎng)絡(luò)算法原理

在整個(gè)人工神經(jīng)網(wǎng)絡(luò)當(dāng)中，BP神經(jīng)網(wǎng)絡(luò)是精華部分，處于核心地位，廣泛用于回歸、逼近、壓縮、識(shí)別等領(lǐng)域。在實(shí)際應(yīng)用中，大約80%的神經(jīng)網(wǎng)絡(luò)模型采取了BP網(wǎng)絡(luò)或BP網(wǎng)絡(luò)的變化形式。BP網(wǎng)絡(luò)大體上由輸入層、隱含層和輸出層組成，其中隱含層可以分為一層或者多層[8]，如圖1所示，該圖是一個(gè)簡(jiǎn)單的神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)示意圖，該神經(jīng)網(wǎng)絡(luò)包含有1個(gè)輸入層、2個(gè)隱含層、1個(gè)輸出層。

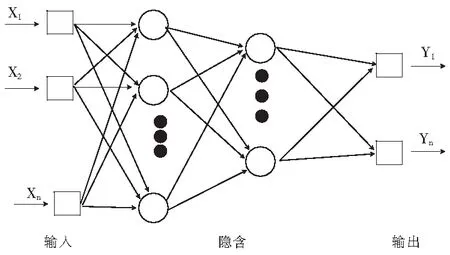
圖1 BP神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)

BP神經(jīng)網(wǎng)絡(luò)的學(xué)習(xí)過程由兩部分組成：正向傳播和反向傳播[9]。把量化的影響因子作為輸入層，在隱含層，網(wǎng)絡(luò)會(huì)自動(dòng)地在地價(jià)與影響因子之間建立非線性映射關(guān)系，賦予每個(gè)影響因子以一定的初始權(quán)重和偏置(即閾值)，然后正向地傳播過去，發(fā)現(xiàn)得出的結(jié)果與給定的結(jié)果之間存在較大的誤差，那么網(wǎng)絡(luò)就會(huì)沿著使誤差遞減速度最快的方向反向傳播，修正權(quán)重和偏置，這個(gè)過程稱為1次迭代，這個(gè)遞減速度也叫做學(xué)習(xí)率。循環(huán)往復(fù)，經(jīng)過多次迭代，直到得到的誤差小于期望誤差，至此，訓(xùn)練結(jié)束。

1.2 BP神經(jīng)網(wǎng)絡(luò)地價(jià)評(píng)估模型

BP神經(jīng)網(wǎng)絡(luò)地價(jià)評(píng)估原理是建立地價(jià)及其影響因素非線性映射關(guān)系，并通過全局優(yōu)化功能去獲取 BP 神經(jīng)網(wǎng)絡(luò)最優(yōu)的初始權(quán)值和閾值， 將這些參數(shù)代入網(wǎng)絡(luò)，然后用仿真模擬函數(shù)進(jìn)行地價(jià)的模擬和預(yù)測(cè)[10]。

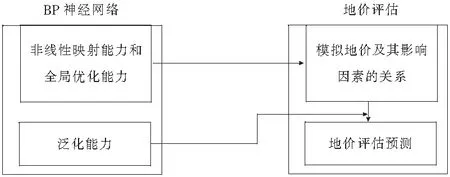
圖2 BP神經(jīng)網(wǎng)絡(luò)地價(jià)評(píng)估原理

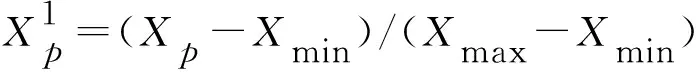
2 實(shí)證研究

2.1 研究區(qū)概況、數(shù)據(jù)來源與處理

本文以南昌市中心城區(qū)建成區(qū)為研究區(qū)(依據(jù)城市總體規(guī)劃確定的城市建成區(qū))。南昌市為江西省的省會(huì)城市，占地面積7 401 km2，地處江西中部偏北，贛江下游，鄱陽(yáng)湖的西南岸，位于東經(jīng)E115°27′～116°35′、北緯N28°10′～29°11′之間。全境山、丘、平原相間，地形主要以平原為主，占總面積35.8%，東南相對(duì)平坦，西北丘陵起伏，水網(wǎng)密布，湖泊眾多。2018年，南昌市全年實(shí)現(xiàn)地區(qū)生產(chǎn)總值(GDP)5 274.67億元，比上年增長(zhǎng)8.9%。其中，第一產(chǎn)業(yè)產(chǎn)值190.68億元，增長(zhǎng)3.2%；第二產(chǎn)業(yè)產(chǎn)值2 660.92億元，增長(zhǎng)8.5%；第三產(chǎn)業(yè)產(chǎn)值2 423.07億元，增長(zhǎng)10.1%。

本文用于地價(jià)評(píng)估的樣本數(shù)據(jù)為2016年南昌市城區(qū)基準(zhǔn)地價(jià)評(píng)估所采用土地交易案例，從中選取了103個(gè)住宅用地交易案例作為樣本點(diǎn)，包括樣本點(diǎn)的容積率、交易價(jià)格等信息。在中國(guó)地價(jià)監(jiān)測(cè)網(wǎng)獲取不同時(shí)期南昌市住宅用地的地價(jià)水平值，以2019年3月1號(hào)為評(píng)估基準(zhǔn)日，將地價(jià)修正到評(píng)估基準(zhǔn)日。住宅地價(jià)樣本點(diǎn)分布如圖3所示，樣本點(diǎn)較為均勻地分布在南昌市主城區(qū)內(nèi)。本文隨機(jī)選取了90個(gè)樣本作為訓(xùn)練樣本集，占樣本總數(shù)的87%，其余13個(gè)樣本作為測(cè)試樣本集，占樣本總數(shù)的13%。

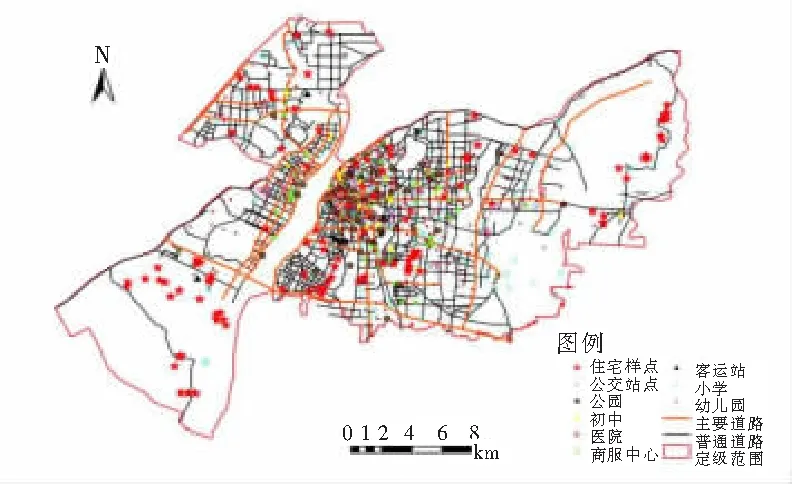
圖3 樣本點(diǎn)分布圖

2.2 住宅地價(jià)影響因素體系構(gòu)建與量化

在選取影響因子時(shí)，參考南昌市城市土地定級(jí)因素因子指標(biāo)體系。1)在影響地價(jià)的商業(yè)因素中選取了商服中心作為影響因子；2)在影響地價(jià)的交通因素中，選取了客運(yùn)站、主要道路、普通道路、公交站點(diǎn)作為影響因子；3)在影響地價(jià)的基礎(chǔ)設(shè)施因素中選取了小學(xué)、初中、幼兒園、醫(yī)院作為影響因子；4)在影響地價(jià)的環(huán)境因素中，選取了公園作為影響因子。影響因子表見表1。

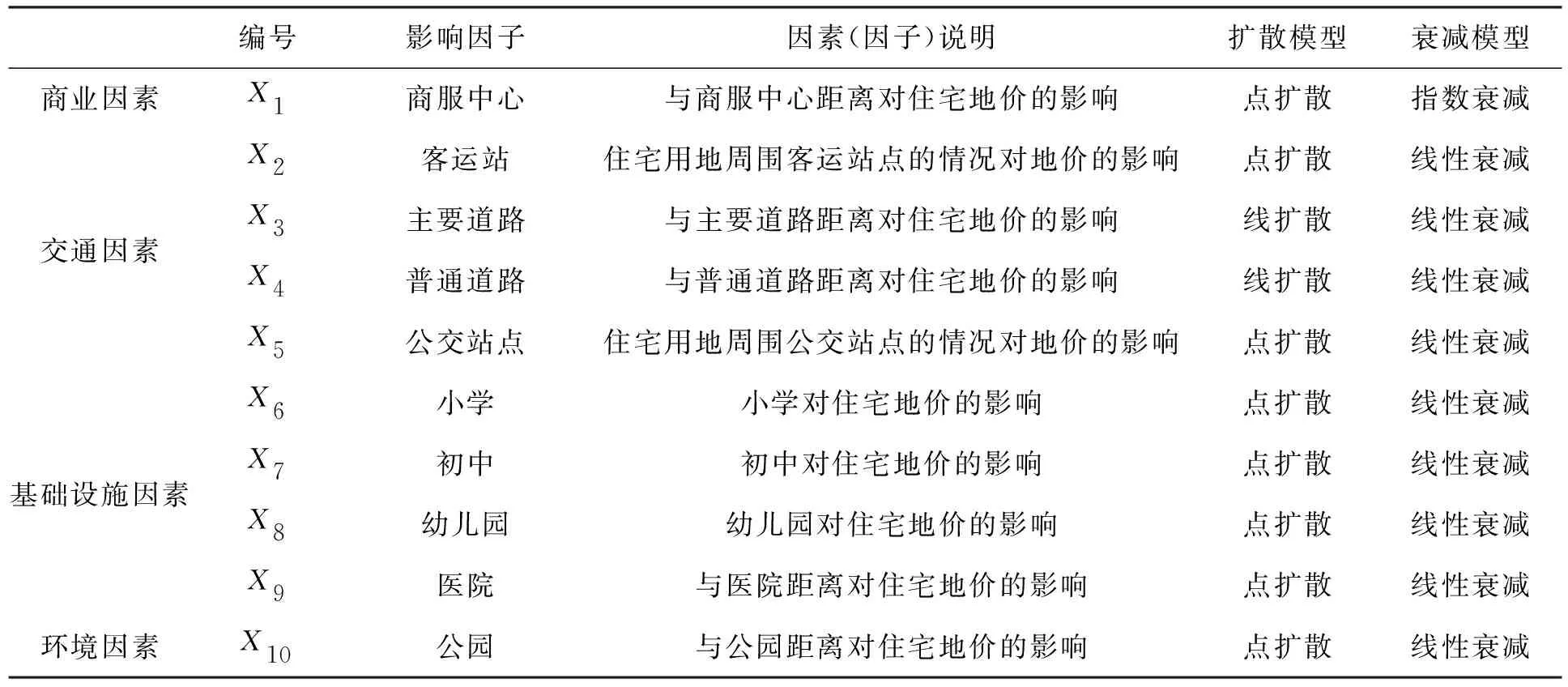
表1 住宅地價(jià)影響因素(因子)表

基礎(chǔ)設(shè)施點(diǎn)狀數(shù)據(jù)通過POI獲取，小學(xué)、公交站點(diǎn)、客運(yùn)站(無坐標(biāo)信息)利用地理編碼獲取經(jīng)緯坐標(biāo)，再將所獲取的點(diǎn)狀要素進(jìn)行投影轉(zhuǎn)換為西安80坐標(biāo)系。

對(duì)影響因子的量化，根據(jù)衰減模型進(jìn)行分值計(jì)算。運(yùn)用ArcGIS空間分析中的歐式距離和柵格計(jì)算器進(jìn)行因子量化，再把計(jì)算出來的值賦予到每個(gè)樣本點(diǎn)上。量化分值范圍為0～100分，分值越高，土地價(jià)格的理論值越高。結(jié)果如圖4所示。

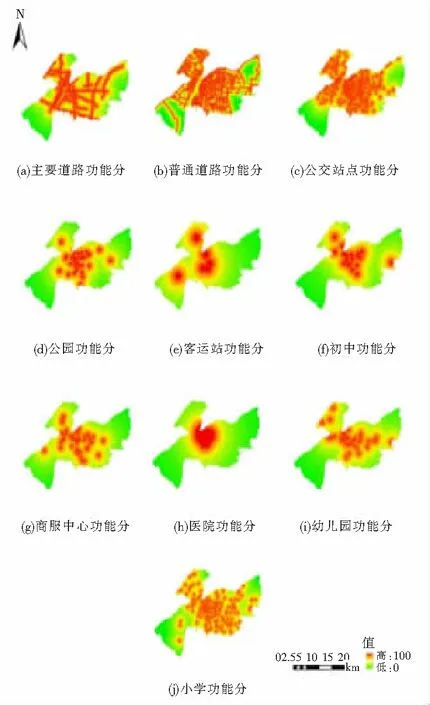
圖4 各影響因子功能分值圖

2.3 相關(guān)分析和灰色關(guān)聯(lián)度分析

為了減小變量間的多重共線性對(duì)模型的影響，現(xiàn)對(duì)影響因子進(jìn)行相關(guān)分析，求出影響因子兩兩間的相關(guān)系數(shù)，發(fā)現(xiàn)公交站點(diǎn)與7個(gè)影響因子顯著相關(guān)，公園與6個(gè)影響因子顯著相關(guān)，商服中心與其他6個(gè)影響因子顯著相關(guān)，幼兒園與6個(gè)影響因子顯著相關(guān)，那么剔除掉這4個(gè)影響因子。

對(duì)剩下的7個(gè)影響因子進(jìn)行灰色關(guān)聯(lián)度分析，檢驗(yàn)其與地價(jià)的關(guān)聯(lián)度大小。灰色關(guān)聯(lián)度是一種衡量因素間關(guān)聯(lián)程度的方法，它是根據(jù)序列曲線形狀與參考序列的曲線形狀的相似程度來計(jì)算關(guān)聯(lián)度大小的。計(jì)算步驟如下。

1)確定比較序列和參考序列，{X1(k)}、{X2(k)}、{X3(k)}、{X4(k)}、{X5(k)}、{X6(k)}、{X7(k)}作為比較序列，{X8(k)}作為參考序列。其中X1為初中，X2為客運(yùn)站，X3為普通道路，X4為小學(xué)，X5為醫(yī)院，X6為主要道路，X7為容積率，X8為修正后地價(jià)。

2)數(shù)據(jù)的無量綱化處理。利用平均值標(biāo)準(zhǔn)化的方法，公式如下：

(1)

計(jì)算灰色關(guān)聯(lián)度。公式如下：

(2)

ζi(k)為灰色關(guān)聯(lián)系數(shù)，ρ為分辨系數(shù)，一般取值為0.5，得到灰色關(guān)聯(lián)度的值為：

(3)

以上過程在DPS 9.01中實(shí)現(xiàn)，得到關(guān)聯(lián)矩陣，其中G(8,1)=0.741 3、G(8,2)=0.749 60、G(8,3)=0.751 29、G(8,4)=0.770 46、G(8,5)=0.749 93、G(8,6)=0.761 17、G(8,7)=0.755 71，關(guān)聯(lián)序：X4>X6>X7>X3>X5>X2>X1。可見，7個(gè)影響因子與地價(jià)的關(guān)聯(lián)程度均大于0.7，對(duì)地價(jià)的影響力大，可以作為模型的解釋變量。

2.4 模型構(gòu)建

2.4.1 訓(xùn)練樣本準(zhǔn)備 經(jīng)過量化后的樣本數(shù)據(jù)，一部分要用來對(duì)BP神經(jīng)網(wǎng)絡(luò)模型進(jìn)行學(xué)習(xí)與訓(xùn)練、從而得到合格的評(píng)估模型，另一部分要用來檢測(cè)該模型的準(zhǔn)確性與可靠性[12]。將每個(gè)住宅樣點(diǎn)在各影響因子下的量化分值作為輸入變量，輸出變量為經(jīng)過時(shí)間修正后的住宅用地交易價(jià)格。

2.4.2 網(wǎng)絡(luò)結(jié)構(gòu)及參數(shù)的確定

1)網(wǎng)絡(luò)層數(shù)的確定。本文選取了7個(gè)影響因子作為輸入變量，故輸入層節(jié)點(diǎn)數(shù)為7個(gè)，地價(jià)作為輸出變量，故輸出層節(jié)點(diǎn)數(shù)為1個(gè)；至于隱含層，一般來說，層數(shù)越多、節(jié)點(diǎn)越多，訓(xùn)練模型上的效果越好，甚至?xí)_(dá)到100%預(yù)期精度。但隨之帶來的問題是過擬合，將模型放在預(yù)測(cè)數(shù)據(jù)上的效果嚴(yán)重降低，而且訓(xùn)練時(shí)間也會(huì)延長(zhǎng)。因此，隱含層數(shù)設(shè)置為1層，根據(jù)節(jié)點(diǎn)公式：

(4)

式中：∝為1～10之間的常數(shù)、n為輸入層節(jié)點(diǎn)數(shù)、m為隱含層節(jié)點(diǎn)數(shù)，因此，確定隱含層節(jié)點(diǎn)數(shù)為8個(gè)[13]。在輸入層與隱含層之間選擇tansig函數(shù)為傳遞函數(shù)，在隱含層與輸出層之間選擇函數(shù)purelin作為傳遞函數(shù)。最終構(gòu)建的網(wǎng)絡(luò)為“7-8-1”的3層網(wǎng)絡(luò)結(jié)構(gòu)。

2)期望誤差的確定。在對(duì)神經(jīng)網(wǎng)絡(luò)訓(xùn)練前，需要設(shè)置一個(gè)期望誤差，期望誤差既不能設(shè)置得過小、也不能設(shè)置得過大。期望誤差過大，會(huì)降低預(yù)測(cè)精度；期望誤差過小，會(huì)導(dǎo)致網(wǎng)絡(luò)還沒有達(dá)到期望誤差就停止訓(xùn)練。根據(jù)經(jīng)驗(yàn)值及多次訓(xùn)練結(jié)果的比較，最終確定期望誤差為0.001。

3)學(xué)習(xí)率的確定。在逆向傳播的過程中，BP神經(jīng)網(wǎng)絡(luò)采用的是隨機(jī)梯度下降算法去調(diào)整權(quán)值和偏置(即閾值)來減小誤差。梯度下降法需要設(shè)置學(xué)習(xí)率，學(xué)習(xí)率決定了一個(gè)小批量中權(quán)重在梯度方向要移動(dòng)多遠(yuǎn)。如果學(xué)習(xí)率過低，盡管訓(xùn)練會(huì)變得更加可靠，但是朝向損失函數(shù)最小值的每個(gè)步長(zhǎng)很小導(dǎo)致優(yōu)化會(huì)耗費(fèi)較長(zhǎng)的時(shí)間。如果學(xué)習(xí)率過高，情況可能會(huì)更糟糕，因?yàn)橛?xùn)練可能不會(huì)收斂，甚至?xí)l(fā)散，權(quán)重的改變量非常大，使得優(yōu)化越過最小值，損失函數(shù)變得更糟[14]。權(quán)重用公式表示為：

(5)

式中：α為學(xué)習(xí)率，θi為權(quán)重值，j(θi)為損失函數(shù)。學(xué)習(xí)率過小(左)和學(xué)習(xí)率過大(右)對(duì)損失函數(shù)的影響如圖9所示。綜合分析，最終確定學(xué)習(xí)率為0.1。

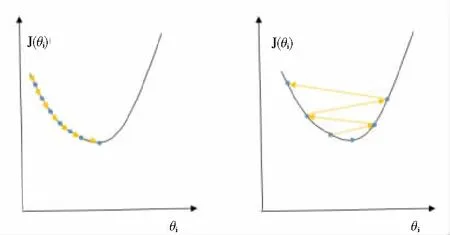
圖5 權(quán)重變化與損失函數(shù)的關(guān)系

4)最大訓(xùn)練迭代次數(shù)。在網(wǎng)絡(luò)訓(xùn)練結(jié)束前，為了讓最后的誤差小于期望誤差，設(shè)置最大的訓(xùn)練迭代次數(shù)為10 000次。

2.5 網(wǎng)絡(luò)運(yùn)行與預(yù)測(cè)結(jié)果

在進(jìn)行BP神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)時(shí)用Matlab語言對(duì)BP網(wǎng)絡(luò)進(jìn)行仿真訓(xùn)練。Matlab工具箱中包含了神經(jīng)網(wǎng)絡(luò)工具箱，為神經(jīng)網(wǎng)絡(luò)的構(gòu)建、訓(xùn)練、模擬、仿真模擬提供了很多函數(shù)，這樣的話，人們?cè)谑褂眠@些函數(shù)時(shí)就不需要編寫復(fù)雜而龐大的算法程序，人們可以根據(jù)自己的需要調(diào)用相關(guān)的程序[15]。

從圖6可以很清楚地看到，模型在147次迭代以后輸出的誤差達(dá)到了設(shè)定的精度，在這個(gè)過程中所花費(fèi)的時(shí)間也很短，僅為數(shù)秒鐘。訓(xùn)練誤差下降很快，在50次以內(nèi)下降得尤其明顯，且從回歸圖來看，線性擬合效果很好，說明網(wǎng)絡(luò)的學(xué)習(xí)狀態(tài)良好。利用仿真模擬sim函數(shù)預(yù)測(cè)后面20組樣本的地價(jià)，用sim函數(shù)預(yù)測(cè)出來的值是歸一化的值，再經(jīng)過反歸一化得到土地價(jià)格。預(yù)測(cè)結(jié)果如圖7所示，預(yù)測(cè)誤差統(tǒng)計(jì)結(jié)果見表2。

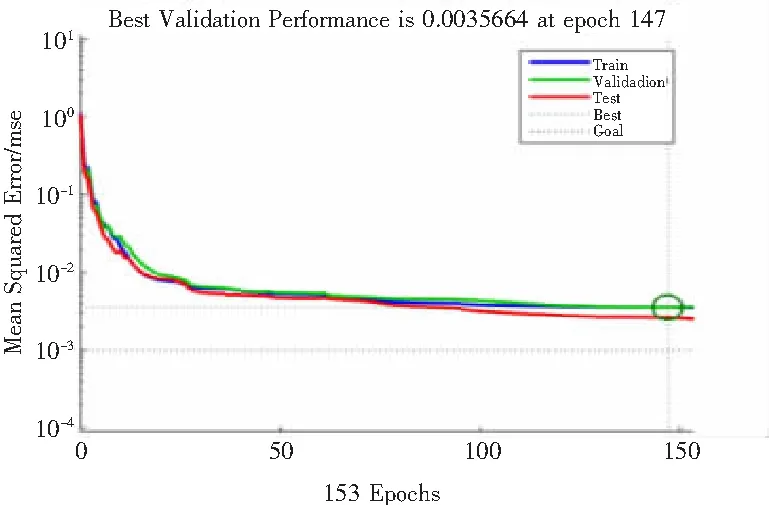
圖6 誤差變化圖與回歸圖

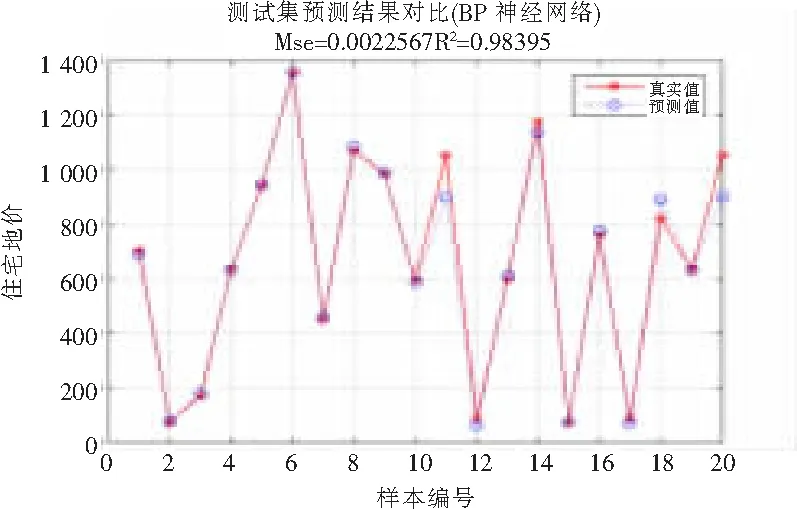
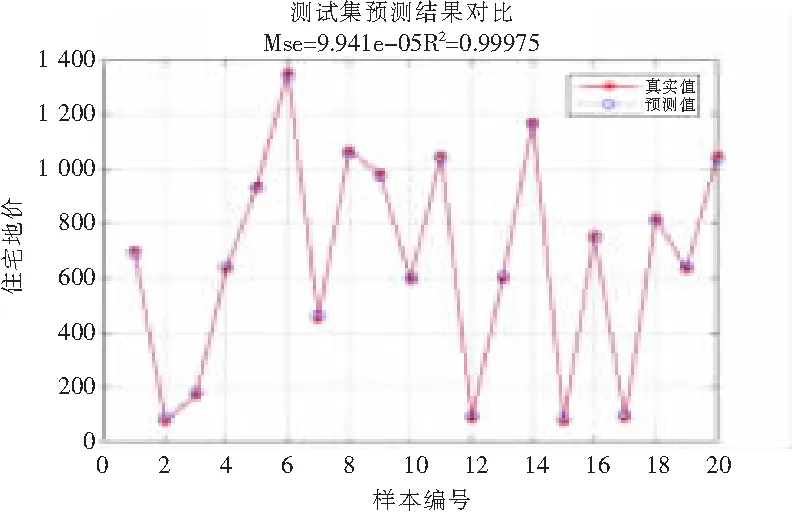
圖7 預(yù)測(cè)輸出(上為BP網(wǎng)絡(luò)，下為SVM模型)

在用BP神經(jīng)網(wǎng)絡(luò)對(duì)地價(jià)進(jìn)行評(píng)估的同時(shí)，作為對(duì)比，也用支持向量機(jī)模型(簡(jiǎn)稱SVM模型)對(duì)地價(jià)進(jìn)行評(píng)估。得到的誤差變化圖與回歸圖以及驗(yàn)證樣本表如下所示：可以看出，無論是BP神經(jīng)網(wǎng)絡(luò)還是SVM模型，得到的預(yù)測(cè)值與實(shí)際值的擬合優(yōu)度都很高，預(yù)測(cè)值與實(shí)際值的誤差百分比也在合理范圍之內(nèi)，沒有偏差太大，只有個(gè)別點(diǎn)的誤差偏大一些，是由于該樣本點(diǎn)的選取不夠合理所致，因?yàn)閷?duì)于該樣本點(diǎn)的預(yù)測(cè)，無論是BP神經(jīng)網(wǎng)絡(luò)還是SVM模型，都出現(xiàn)較大誤差。總的來說，BP神經(jīng)網(wǎng)絡(luò)對(duì)地價(jià)的預(yù)測(cè)是比較精確的。

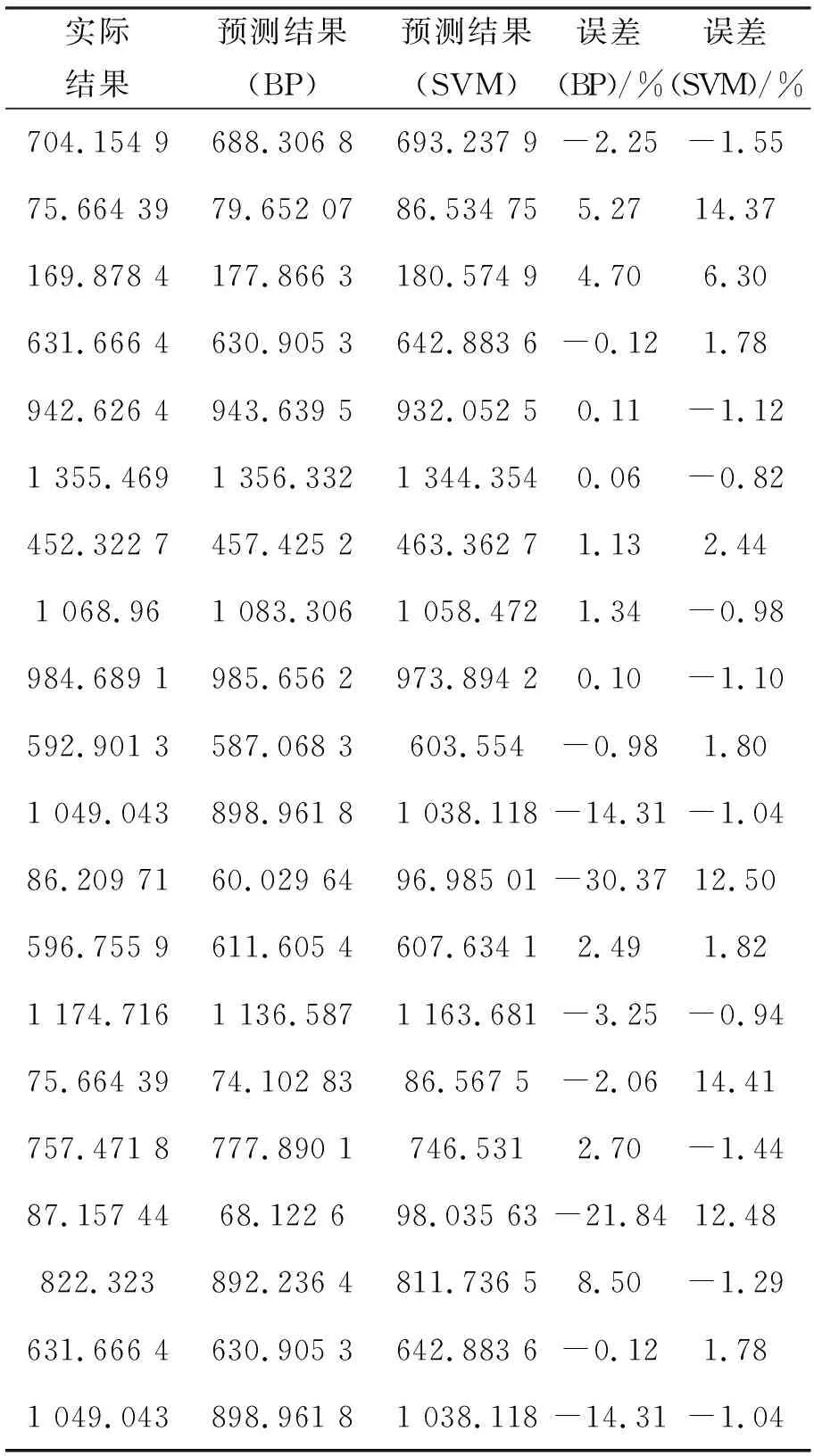
表2 驗(yàn)證樣本表

值得一提的是，盡管SVM模型給出的預(yù)測(cè)值的誤差要小于BP神經(jīng)網(wǎng)絡(luò)，但是SVM模型在整個(gè)運(yùn)行過程中用了數(shù)分鐘才完成，而BP神經(jīng)網(wǎng)絡(luò)只用了數(shù)秒鐘。BP神經(jīng)網(wǎng)絡(luò)的運(yùn)行效率要遠(yuǎn)遠(yuǎn)高于SVM模型，SVM模型對(duì)計(jì)算機(jī)的運(yùn)算性能有更高的要求。綜合預(yù)測(cè)精度跟運(yùn)算性能兩者來考慮的話，BP神經(jīng)網(wǎng)絡(luò)要好一些。

3 結(jié)論與討論

本文以南昌市主城區(qū)的住宅地價(jià)作為研究對(duì)象，根據(jù)影響地價(jià)的主要因素，選取了商服中心、客運(yùn)站、主要道路、普通道路、公交站點(diǎn)、小學(xué)、初中、幼兒園、醫(yī)院、公園等作為影響因子，再獲取量化分值。經(jīng)過相關(guān)分析和灰色關(guān)聯(lián)度分析，剔除掉了公交站點(diǎn)、公園、商服中心、幼兒園4個(gè)影響因子。用前83組樣本進(jìn)行訓(xùn)練，找出最優(yōu)權(quán)重和閾值，再用仿真模擬函數(shù)對(duì)剩下的20組樣本進(jìn)行預(yù)測(cè)。結(jié)果顯示預(yù)測(cè)值與實(shí)際值的誤差控制在合理范圍以內(nèi)，表明BP神經(jīng)網(wǎng)絡(luò)模型進(jìn)行地價(jià)預(yù)測(cè)是可行的，且預(yù)測(cè)精度較高。

BP神經(jīng)網(wǎng)絡(luò)有著強(qiáng)大的非線性映射能力，能夠在影響因素與地價(jià)之間迅速建立起一種聯(lián)系。跟傳統(tǒng)估價(jià)方法中的市場(chǎng)比較法相比，BP神經(jīng)網(wǎng)絡(luò)有很多相似之處，不同的是，BP神經(jīng)網(wǎng)絡(luò)不需要人為確定修正系數(shù)，這也就在很大程度上降低了人為因素對(duì)估價(jià)的影響，使得估價(jià)的過程更加符合評(píng)估的三大原則：獨(dú)立、客觀、公正。

用神經(jīng)網(wǎng)絡(luò)對(duì)地價(jià)進(jìn)行評(píng)估仍存在兩大缺陷：一是用BP網(wǎng)絡(luò)進(jìn)行評(píng)估時(shí)，要選取具體的、可以量化的影響因子。也就是說，神經(jīng)網(wǎng)絡(luò)只能進(jìn)行定量分析。但是在影響地價(jià)的因素當(dāng)中，有些只能進(jìn)行定性分析，如國(guó)家宏觀政策對(duì)地價(jià)的影響；二是用BP網(wǎng)絡(luò)評(píng)估地價(jià)從本質(zhì)上來說，與市場(chǎng)比較法是一致的。訓(xùn)練樣本即為可比交易案例，根據(jù)可比交易案例的情況，來預(yù)測(cè)待估宗地地價(jià)。因此，市場(chǎng)法適用的BP網(wǎng)絡(luò)也適用，市場(chǎng)法的局限性也是BP網(wǎng)絡(luò)的局限性。對(duì)于劃撥出讓、協(xié)議出讓或者市場(chǎng)不活躍的土地價(jià)格的確定，BP神經(jīng)網(wǎng)絡(luò)不適用，因其交易價(jià)格無法獲取。即便如此，對(duì)于南昌市城區(qū)住宅用地地價(jià)評(píng)估來說，BP神經(jīng)網(wǎng)絡(luò)是適用的。

隨著智能化時(shí)代的到來，類似于BP神經(jīng)網(wǎng)絡(luò)的人工智能方法將會(huì)應(yīng)用到各行各業(yè)中，將BP神經(jīng)網(wǎng)絡(luò)應(yīng)用到土地估價(jià)當(dāng)中，也會(huì)推動(dòng)我國(guó)土地估價(jià)工作的發(fā)展，為政府和經(jīng)濟(jì)主體參與經(jīng)濟(jì)活動(dòng)提供科學(xué)的依據(jù)。