OFDM序列調制的信息分組映射方法研究
閻肖鵬,馮旭東,付 軍
(中國人民解放軍91550部隊,遼寧 大連 116023)
0 引言
序列調制[1](Index Modulation,IM),又稱為序號調制,是近年來被廣泛研究的一種新型調制技術,其可看作是廣義空間調制(General Spatial Modulation,GSM)中基于天線組合的信息承載方法向全信息傳輸要素的一種推廣[2-4]。在IM技術中,通信系統中任意種類的數量為2個以上的傳輸要素均可用于加載信息,如天線、子載波、中繼節點、調制種類、時隙/采樣間隔、預編碼矩陣和擴頻碼等。正交頻分復用(Orthogonal Frequency Division Multiplexing,OFDM)是目前應用最廣泛的多載波技術,其在頻譜利用率、抗多徑和易于實現等方面具有明顯優勢,其缺點是多路時域疊加信號的峰均功率比(Peak-to-Average Power Ratio,PAPR)較高。OFDM序列調制(OFDM with Index Modulation,OFDM-IM)是IM與OFDM的結合,其通過選擇若干個子載波的組合并調制來加載信息,在相同的功率效率情況下,有望獲得比傳統OFDM更高的帶寬效率,并可有效降低系統的PAPR[5-7]。
OFDM-IM方法從提出至今不過十年時間,還有很多理論問題和關鍵技術需要解決。在目前的OFDM-IM調制模型中,其原始信息分2次進行調制,第1次是選擇子載波組合,第2次是對所選擇的子載波進行正交振幅(Quadrature Amplitude Modulation,QAM)調制或多進制數字相位(Multiple Phase Shift Keying,MPSK)調制[8-14]。在這種方式下,2次調制是分別進行的,沒有從系統可靠性入手對信息映射方式進行總體設計,導致調制信號間的最小歐式距離沒有優化,影響了該調制方法的性能。本文對OFDM-IM的信息分組映射方法進行了研究,將APSK調制引入OFDM-IM中,針對其多圈星座圖構建問題,結合APSK-OFDM-IM調制信號形式,提出了多圈窮舉搜索的星座圖構建方法,并以提升系統誤碼率性能為目標,提出了基于APSK-OFDM-IM的信息分組映射方法。
1 OFDM-IM調制模型
假設OFDM系統的子載波數目為n,在OFDM-IM方法中,一般將所有子載波均分為若干組,每個組再分別進行序列調制。假設將子載波分為g組,在每組內進行序列調制,選出的子載波再進行傳統數字調制。每組子載波數為n/g,每組中選出k個子載波,這k個子載波進行l進制的數字調制,則一次調制可承載的信息量p為:
p=g(?lbC(n/g,k)」+lbl)。
每個小組的信息量為p/g,令p1=?lbC(n/g,k)」,p2=lbl,則p/g=p1+p2。在OFDM-IM的2組信息映射中,第1組映射加載p1比特的信息,第2組加載p2比特的信息,在完成信息映射分組后,采用傳統OFDM的FFT方法,即可完成載波調制,后續流程與傳統OFDM方法一致。OFDM-IM調制的基本流程如圖1所示。
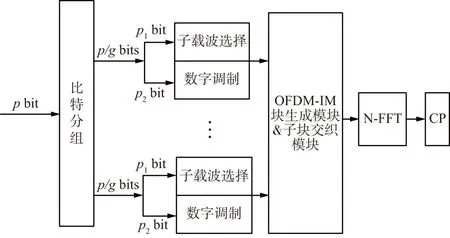
圖1 OFDM-IM調制的基本流程Fig.1 The schematic diagram of OFDM-IM
假設子載波數n=8,子載波數索引集合為{1,2,3,4,5,6,7,8},分組數g=2,則每組4個載波,每次參加序列調制的子載波數k=2,則p1=?lbC(n/g,k)」=2。對于每個子載波,再采用4-PSK或QAM調制。在第1組中,信息比特與子載波索引組合的對應關系如表1所示。
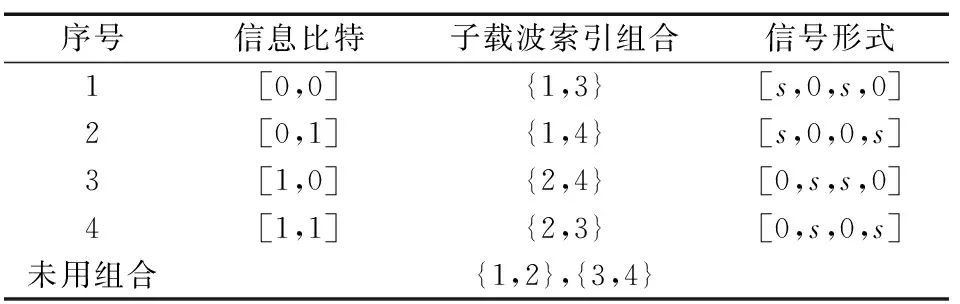
表1 信息比特與子載波組合對應關系表Tab.1 The relationship between the information bit and sub-carrier combination
需要說明的是,為了提高系統的誤碼率性能,當lbC(n/g,k)不是整數,即可選的脈沖組合有冗余時,一般選擇載波中心頻率相差較遠的脈沖組合。如表1中,{1,2}和{3,4}這2組脈沖組合是未用的。
2 基于APSK調制的信息分組映射方法
在OFDM-IM調制方法中,數字調制部分一般對各個子載波單獨進行QAM或MPSK調制,再生成子載波調制信號并交織。對于OFDM-IM調制方法,由于每次調制無法利用所有子載波,為了達到與OFDM相同的頻譜效率,就需要對每個子載波進行更高進制的PSK或QAM調制。在各子載波數字調制這一環節中,現有的OFDM-IM方法采用傳統MPSK或M-QAM調制方法,MPSK主要是將調制星座圖中的單元圓進行等間隔取點,以獲得代表各相位的調制信號,而M-QAM方法一般采用等幅度矩形星座圖的方式,獲得各調制信號形式。上述2種方法對傳統OFDM信號可達到最優的誤碼率性能,由于OFDM-IM信號各子載波并不是等間隔分布,仍采用單一幅度等間隔劃點或等間隔幅度的方式進行調制信息向子載波的加載,將導致系統誤碼率性能降低,同時,在高傳輸速率要求下,仍采用傳統數字調制方式的OFDM-IM信號將具有較大的PAPR。
為解決上述問題,這里將APSK調制引入OFDM-IM中,提出了APSK多圈分組信息映射方法。對于APSK調制,首先要確定其星座圖分布,星座圖分布確定后,其信息映射方式也就確定了[15]。這里針對OFDM-IM調制信號的形式,對APSK調制星座圖重新進行了設計。由于OFDM-IM調制的理論誤碼率性能由調制信號的最小歐式距離決定,這里以最小歐式距離最大化為目標,對其星座圖進行了設計。
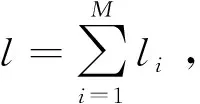
① 根據子載波數目k和調制階數l,確定APSK的調制圈數M=「lbl/2k?;
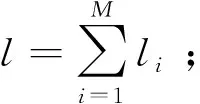
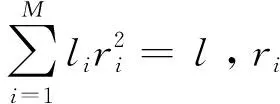
④ 確定各相鄰圈的旋轉角度,對于第i圈和第i+1圈,第i+1圈的旋轉角度Δθi,i+1=π/LCM(li,li+1),i=1,2,…,M-1;
⑤ 計算每次遍歷所得調制信號的最小歐式距離,記錄其最大值所對應的各圈調制階數和半徑的組合,即為最優星座圖組合。
基于APSK調制分組映射的OFDM-IM調制方法原理如圖2所示。

圖2 基于APSK分組映射的OFDM-IM方法原理Fig.2 The schematic diagram of OFDM-IM based on APSK grouping mapping
該方法中,比特分組后,一部分進行子載波序列調制,另一部分進行APSK分組映射。APSK分組映射中,首先需要按照上述搜索步驟確定APSK最優星座圖設計;在確定APSK最優星座圖組合后,APSK分圈策略也相應確定,對于APSK的每一圈內,星座點采用等間隔方式劃分,即相當于MPSK調制。根據APSK的星座圖分布,再在每一圈上分別進行MPSK調制,從而完成該組子載波的數字調制。在完成該組序列調制比特映射后,后續步驟與OFDM-IM相同。
3 算法仿真與分析
為了驗證算法的可行性和準確性,在Matlab仿真環境中,對該方法的性能進行了仿真分析,并與相同頻譜效率的QAM-IM-OFDM調制方法進行了比較。
假設子載波數n=8,子載波數索引集合為{1,2,3,4,5,6,7,8},分組數g=2,則每組4個載波,在參加序列調制的子載波數k=2,數字調制進制數l=16,以及k=3,l=32兩種情況下,分別對APSK星座圖進行了設計,并給出了相應的信息分組映射方案。2種情況下構建的APSK分圈如表2所示。

表2 最優多圈APSK星座圖參數Tab.2 The optimal parameters of APSK multi-ring constellation
在調制子載波數k=2,數字調制進制數l=16,APSK分組映射方法采用表2中第1行的星座圖,此時第1,2圈之間的旋轉角度Δθ1,2=π/8。對APSK分組映射方法、傳統QAM和MPSK三種方法下的OFDM-IM誤碼率性能進行了仿真,結果如圖3所示。
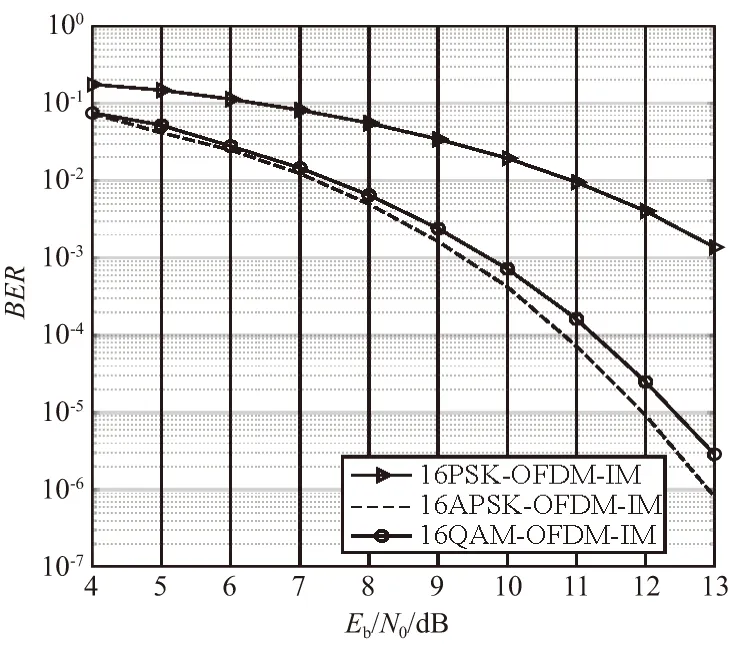
圖3 16進制時3種典型OFDM-IM調制的 誤碼率性能仿真結果Fig.3 The BER simulation results of three OFDM-IM hexadecimal modulations
由圖3可知,在16進制情況下,與16PSK-OFDM-IM調制方法相比,APSK分組映射方法的誤碼率性能有較大優勢,在Eb/N0=12 dB情況下,其誤碼率性能有2個數量級的優勢。在BER=10-5情況下,APSK分組映射方法相對于16QAM-OFDM-IM調制方法有較小優勢,約為0.5 dB,且優勢隨信噪比的升高而增加。
在調制子載波數k=3,數字調制進制數l=32時,對APSK分組映射方法和傳統QAM和MPSK調制方法下的OFDM-IM的誤碼率性能進行了仿真,結果如圖4所示。APSK分組映射方法采用表2中第2行的星座圖,此時第1,2圈之間的旋轉角度為Δθ1,2=π/247。
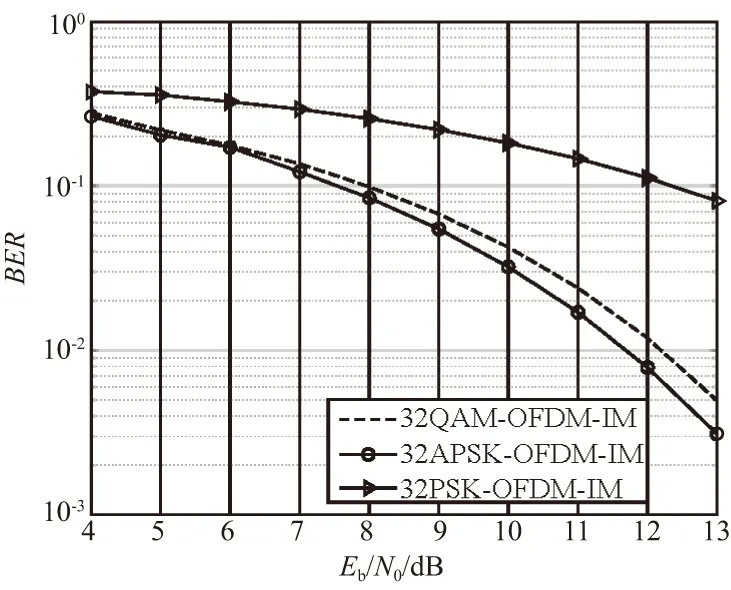
圖4 32進制時3種典型OFDM-IM調制的 誤碼率性能仿真結果Fig.4 The BER simulation results of three OFDM-IM 32-ary modulations
由圖4可知,在32進制情況下,與32PSK-OFDM-IM調制方法相比,APSK分組映射方法的誤碼率性能有較大優勢,在Eb/N0=12 dB情況下,其誤碼率性能約有一個數量級的優勢。與16進制情況下的仿真結果類似,APSK分組映射方法相對于QAM-OFDM-IM調制方法有較小的優勢,且優勢隨信噪比的升高而增加。綜合以上2次仿真結果可以看出,與OFDM-IM所采用的傳統多進制調制方法相比,APSK分組映射方法增加了OFDM-IM調制信號的最小歐式距離,提升了系統的誤碼率性能。
4 結束語
載波序列調制方法在提高系統調制容量上具有明顯的優勢。目前,針對載波序列調制所用的二級信息映射模式展開研究,為進一步提升系統誤碼率性能,提出了基于APSK調制的信息分組映射方法,建立了相應的APSK多圈星座圖優化模型,給出APSK-OFDM-IM的原理框圖。仿真結果表明,與OFDM序列調制二級信息映射方法相比,該方法可提高調制信號的最小歐式距離,有效提升系統的誤碼率性能,具有較好的應用前景。

