基于流形距離核的自適應(yīng)遷移譜聚類(lèi)算法
齊曉軒 都 麗 洪振麒
1(沈陽(yáng)大學(xué)應(yīng)用技術(shù)學(xué)院 遼寧 沈陽(yáng) 110044)2(沈陽(yáng)大學(xué)信息工程學(xué)院 遼寧 沈陽(yáng) 110044)
0 引 言
聚類(lèi)[1-2]作為數(shù)據(jù)挖掘領(lǐng)域中重要的方法,主要是將同類(lèi)對(duì)象劃分為同一簇,不同類(lèi)對(duì)象劃分到不同簇的過(guò)程。聚類(lèi)方法有很多種,如C-means、FCM、MECA[3-5]等算法,但這些算法在高斯分布數(shù)據(jù)集上聚類(lèi)效果良好,在非高斯分布數(shù)據(jù)集上聚類(lèi)效果卻不太理想,容易受樣本形狀影響。譜聚類(lèi)算法(SC)[6-10]作為一種圖論演化而來(lái)的算法,不受樣本空間形狀的制約,且收斂于全局最優(yōu)解,在一定程度上解決了這個(gè)問(wèn)題。
SC算法首先根據(jù)給定的樣本集計(jì)算任意兩點(diǎn)的相似度矩陣W,然后計(jì)算特征矩陣,最后使用特征矩陣進(jìn)行聚類(lèi),所以相似度矩陣W的選取直接影響特征矩陣的構(gòu)造,進(jìn)而影響聚類(lèi)效果。Kong等[10]通過(guò)建立新的相似圖來(lái)構(gòu)造相似度矩陣;ZelnikManor等[13]利用數(shù)據(jù)點(diǎn)的鄰域分布,自動(dòng)調(diào)節(jié)尺度參數(shù),增加其泛化能力。Wang等[3]針對(duì)相似度矩陣構(gòu)造存在尺度敏感問(wèn)題,利用密度差來(lái)調(diào)整樣本點(diǎn)之間的相似度。范子靜等[14]利用模糊劃分改進(jìn)譜聚類(lèi)中硬化分,調(diào)整相似性度量函數(shù)。以上方法皆是以歐氏距離作為相似性度量方法,無(wú)法反映空間分布結(jié)構(gòu)特征。張建朋等[15]通過(guò)使用流形距離代替歐氏距離構(gòu)造相似性矩陣來(lái)改進(jìn)AP算法,較好地解決了數(shù)據(jù)分布的全局結(jié)構(gòu)問(wèn)題;Tao等[16]使用流形距離計(jì)算相似度矩陣,但沒(méi)有考慮數(shù)據(jù)點(diǎn)全部的鄰域信息,對(duì)于復(fù)雜分布點(diǎn)效果依然不理想。
在實(shí)際環(huán)境中,領(lǐng)域中可用數(shù)據(jù)的匱乏或者數(shù)據(jù)受到污染,樣本特征信息稀疏,傳統(tǒng)的聚類(lèi)算法很難達(dá)到良好效果。針對(duì)此種情況,遷移學(xué)習(xí)可以有效利用在某個(gè)不同但相關(guān)領(lǐng)域上學(xué)習(xí)到的知識(shí)或模式(源域)指導(dǎo)當(dāng)前領(lǐng)域(目標(biāo)域)中數(shù)據(jù)量匱乏的聚類(lèi)任務(wù),輔助提高聚類(lèi)效果。在聚類(lèi)中加入遷移學(xué)習(xí)已幫助學(xué)者們解決了很多問(wèn)題[16-19]:Dai等[20]通過(guò)同時(shí)聚類(lèi)目標(biāo)和輔助數(shù)據(jù)提出一種基于協(xié)同聚類(lèi)的自學(xué)習(xí)聚類(lèi)(STC);Jiang等[21]通過(guò)聯(lián)合聚類(lèi)方法提出遷移譜聚類(lèi)方法(TSC);魏彩娜等[22]提出基于F-范數(shù)正則項(xiàng)的遷移譜聚類(lèi)方法(TSC-IDFR);Qian等[23]提出使用中心與隸屬度信息遷移的TI-KT-CM和TII-KT-CM方法。
為提高譜聚類(lèi)的領(lǐng)域適應(yīng)能力,降低樣本數(shù)量、數(shù)據(jù)空間分布對(duì)譜聚類(lèi)的性能影響,本文提出一種基于流形距離核的自適應(yīng)遷移譜聚類(lèi)算法。具體包括兩個(gè)方面的改進(jìn):① 考慮數(shù)據(jù)分布的全局一致性,使用流形距離作為相似性計(jì)算方法,且面對(duì)簇邊緣分布不均勻或不同簇邊緣分布密度相近,局部密度情況復(fù)雜會(huì)導(dǎo)致錯(cuò)分的問(wèn)題,對(duì)核函數(shù)進(jìn)行自適應(yīng)調(diào)整,提高譜聚類(lèi)對(duì)復(fù)雜數(shù)據(jù)集的處理能力;② 考慮領(lǐng)域數(shù)據(jù)匱乏問(wèn)題,引入遷移學(xué)習(xí)方法,使用源域的知識(shí)輔助目標(biāo)域進(jìn)行譜聚類(lèi)。經(jīng)實(shí)驗(yàn)驗(yàn)證,本文算法與原始譜聚類(lèi)算法相比有明顯提升。
1 相關(guān)概念
1.1 SC算法
SC算法(見(jiàn)圖1)主要思想是把樣本點(diǎn)連接起來(lái)構(gòu)造無(wú)向權(quán)重圖,根據(jù)距離遠(yuǎn)近賦予權(quán)重高低,根據(jù)子圖內(nèi)權(quán)重和高、子圖間權(quán)重和低的最優(yōu)劃分原則對(duì)圖進(jìn)行最優(yōu)劃分,從而完成聚類(lèi)。
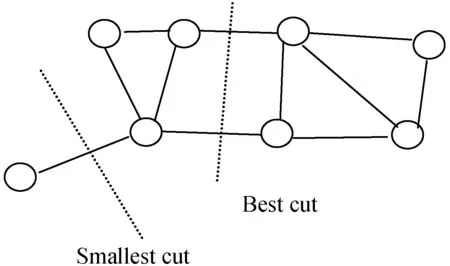
圖1 SC算法原理示意圖
SC算法的最優(yōu)化模型為:
maxtr(UTLU)U∈RN×k
(1)
s.t.UTU=I
算法實(shí)現(xiàn)過(guò)程:
輸入:n個(gè)樣本點(diǎn)X=x1,x2,…,xn,聚類(lèi)個(gè)數(shù)k
輸出:聚類(lèi)簇c1,c2,…,ck
步驟1構(gòu)造無(wú)向權(quán)重圖G(V,E),計(jì)算相似度矩陣W:
(2)
步驟2計(jì)算度矩陣D:
(3)
步驟3計(jì)算拉普拉斯矩陣L:
L=D-W
(4)
標(biāo)準(zhǔn)化L:
(5)
步驟4計(jì)算L的前k個(gè)最小特征值的特征向量組成矩陣且對(duì)其進(jìn)行標(biāo)準(zhǔn)化,得到特征矩陣U={u1,u2,…,uk},U∈Rn×k。
步驟5采用C-means或FCM等對(duì)U進(jìn)行聚類(lèi),得到聚類(lèi)結(jié)果{c1,c2,…,ck}。
1.2 流形距離
歐氏距離是最快捷簡(jiǎn)單的距離度量方法。但使用歐氏距離計(jì)算的聚類(lèi)算法往往會(huì)忽略數(shù)據(jù)的空間分布特征,無(wú)法滿(mǎn)足聚類(lèi)的全局一致性。為了解決這個(gè)問(wèn)題,有學(xué)者提出流形距離,具體形式如下:
局部流形距離即流形上的點(diǎn)到點(diǎn)的線段長(zhǎng)度,在同一流形結(jié)構(gòu)中,數(shù)據(jù)集任意兩點(diǎn)xi、xj之間的流形距離為:
Ld(xi,xj)=ρdist(xi,xj)-1
(6)
式中:dist(xi,xj)為xi和xj兩點(diǎn)之間的歐氏距離。
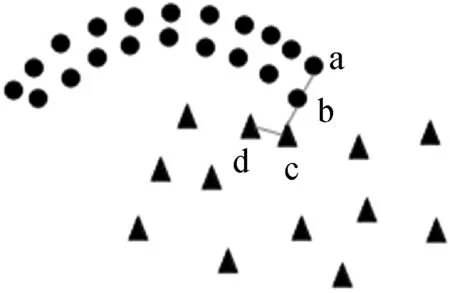
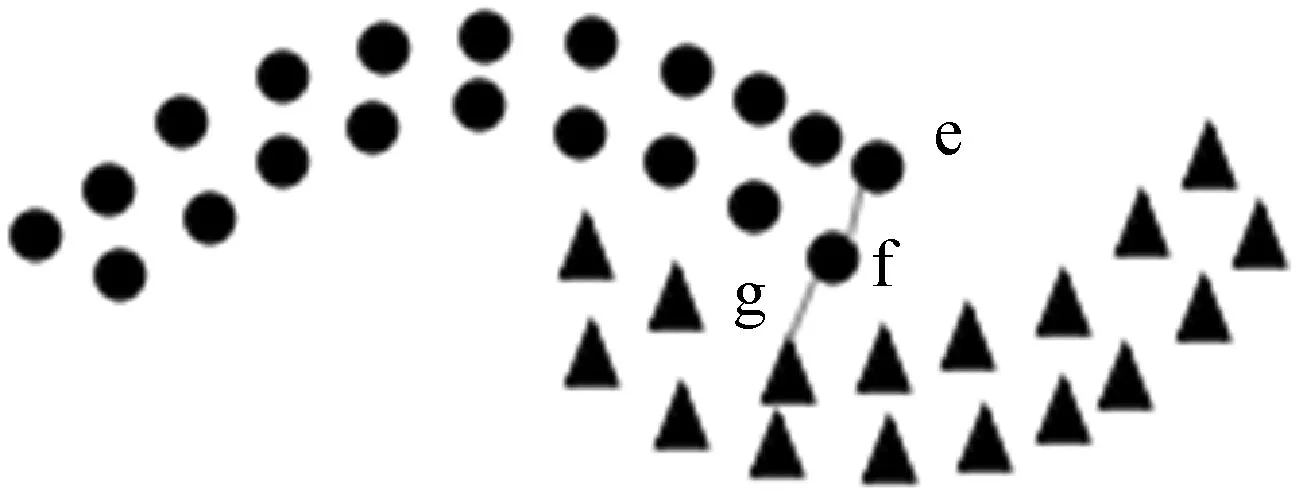
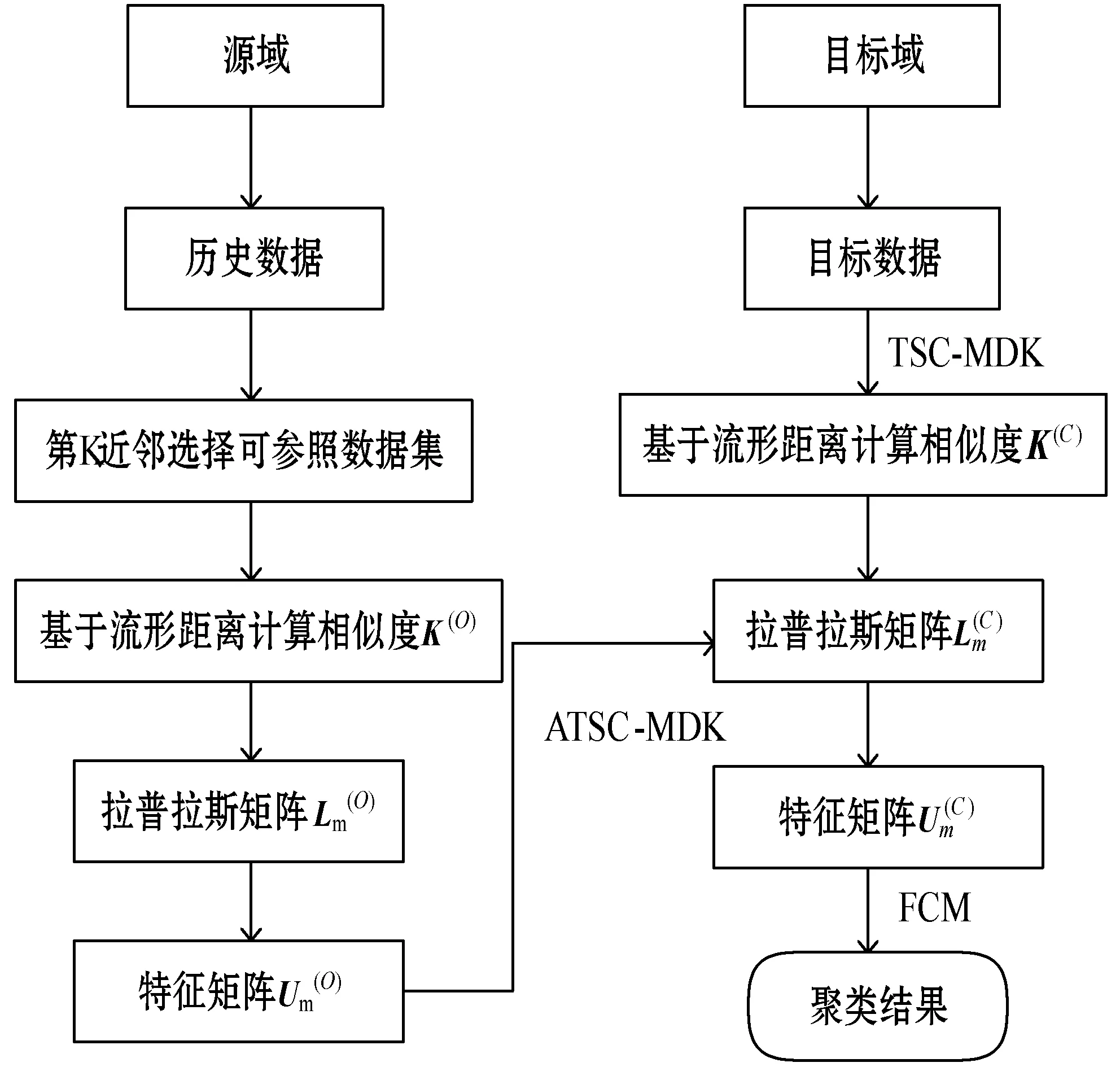
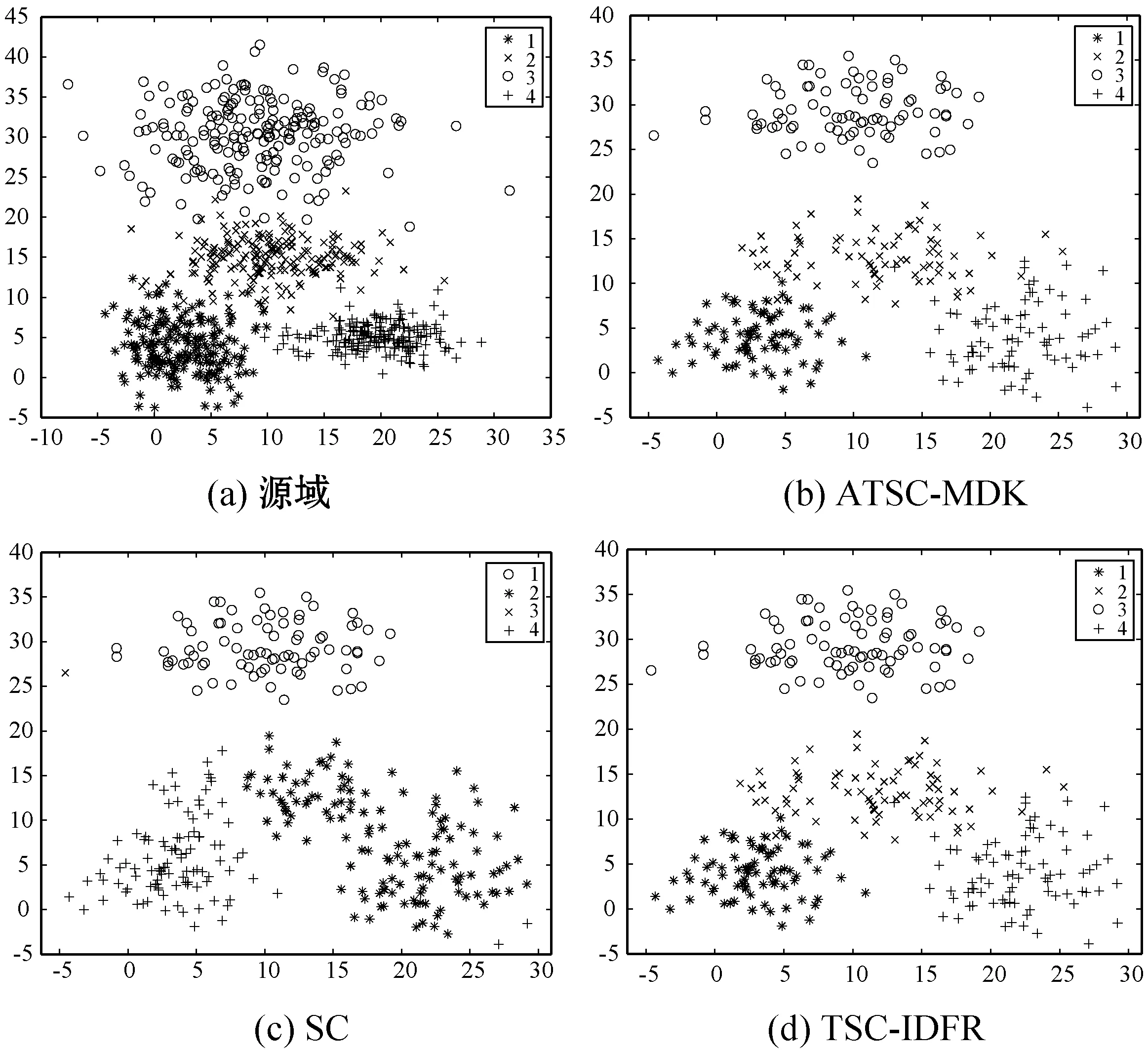
全局流形距離:構(gòu)造數(shù)據(jù)點(diǎn)間的加權(quán)無(wú)向圖G(V,E),V為圖的頂點(diǎn),E為圖邊集合。令p={p1,p2,…,pk}∈Vl表示圖上一條連接點(diǎn)p1與pk的路徑,其中邊(pm,pm+1)∈E,1≤m 設(shè)P=(p1,p2,…,pk)是xi和xj之間的一條最短路徑,則全局流形距離為連接兩點(diǎn)之間的最短路徑的所有局部距離之和: (7) 式中:pi,j是xi和xj之間的最短路徑。 (8) 該方法可增大不同流形上數(shù)據(jù)點(diǎn)的距離,縮小不同流形上數(shù)據(jù)點(diǎn)的距離。 SC算法用高斯核函數(shù)構(gòu)建相似度矩陣,但是歐氏距離在計(jì)算距離時(shí)受結(jié)構(gòu)影響較大,當(dāng)數(shù)據(jù)集為復(fù)雜的流形結(jié)構(gòu)時(shí),會(huì)損失很多結(jié)構(gòu)特征,使用流形距離代替歐氏距離能在一定程度上解決這個(gè)問(wèn)題。 本文以流形距離計(jì)算任意兩點(diǎn)的距離,且對(duì)核函數(shù)進(jìn)行調(diào)整,使其面對(duì)更復(fù)雜的分布時(shí),保留更多樣本特征信息,提高聚類(lèi)準(zhǔn)確率。歐氏距離計(jì)算的核函數(shù)為: (9) 本文用流形距離作為距離度量方法,流形距離核函數(shù)為: (10) 該核函數(shù)雖能考慮數(shù)據(jù)的整體結(jié)構(gòu)分布,但參數(shù)σ均是通過(guò)反復(fù)測(cè)試得到,時(shí)間復(fù)雜度高,若取固定值,則影響核函數(shù)的泛化性,制約聚類(lèi)效果。為了取得合適參數(shù),ZelnikManor等[13]提出使用數(shù)據(jù)點(diǎn)的鄰域信息計(jì)算一種自動(dòng)選擇尺度參數(shù)σ的方法,為每一個(gè)樣本點(diǎn)選擇一個(gè)σi,定義的核函數(shù)為: (11) 式中:σi為點(diǎn)xi到第k個(gè)近鄰的歐氏距離,但該k近鄰方法易受噪聲點(diǎn)影響。本文尺度參數(shù)取點(diǎn)xi的加權(quán)距離,可在一定程度上提高核函數(shù)的自適應(yīng)能力,降低噪聲點(diǎn)的干擾,具體表示為: (12) (13) 式中:參數(shù)σi取點(diǎn)xi的第k個(gè)近鄰點(diǎn)xk的加權(quán)距離。由此可以得到融入加權(quán)參數(shù)和流形距離的核函數(shù),具體表示為: (14) 使用流形距離計(jì)算的相似度矩陣考慮了全局一致性,加權(quán)參數(shù)可減小參數(shù)對(duì)特征矩陣的影響。但當(dāng)簇間密度差異較大、簇邊緣分布不均勻或不同簇邊緣分布密度相近時(shí),局部密度情況復(fù)雜會(huì)導(dǎo)致錯(cuò)分,仍會(huì)影響聚類(lèi)效果。以圖2和圖3為例,利用式(14)計(jì)算圖2中點(diǎn)的相似度,a、b位于較稠密的簇中,c、d處于較稀疏的簇中,且它們都處于簇的邊緣,正確聚類(lèi)有一定難度,已知dist(a,b)=dist(b,c)=dist(c,d),可知當(dāng)σb<σd、σbσc<σdσc,得K(b,c) 圖2 樣密度分布不均勻示意圖 圖3為雙月形分布,已知dist(e,f)=dist(f,g),當(dāng)σe=σg時(shí),σeσf=σgσf,表明e、f和g、f的相似度相同,但e、f應(yīng)聚為一類(lèi),所以g影響了f的聚類(lèi),可能使f聚為錯(cuò)誤的一類(lèi)。所以應(yīng)該賦予e、f更高的相似性。 圖3 雙月形分布示意圖 為解決上述問(wèn)題,提高聚類(lèi)準(zhǔn)確率,本文使用共享近鄰方法(SNN)[24]來(lái)調(diào)整相似度矩陣,SNN定義為求兩個(gè)點(diǎn)共享的近鄰點(diǎn)的個(gè)數(shù)。xi和xj表示樣本集{x1,x2,…,xn}的任意兩點(diǎn),兩點(diǎn)的相似度為共享最近鄰點(diǎn)的個(gè)數(shù),即: (15) (16) 當(dāng)共享近鄰數(shù)為0時(shí),SNN(xi,xj)+1=1,即對(duì)相似性不作調(diào)整。因?yàn)閍、b處于稠密的簇中,可知a、b的共享近鄰的個(gè)數(shù)多于b、c的共享近鄰個(gè)數(shù),所以SNN(a,b)+1>SNN(b,c)+1,可以對(duì)相似性進(jìn)行調(diào)整,使a、b的相似性更大,使聚為一類(lèi)的概率更高。e、f處于同一流形中,g處于另一流形中,可知e、f共享近鄰多于g、f,所以SNN(e,f)+1>SNN(f,g)+1,可以對(duì)相似性進(jìn)行調(diào)整,使e、f的相似性更大,更可能聚為一類(lèi)。 綜上,基于SC算法提出了一種改進(jìn)的計(jì)算相似度函數(shù)的方法:“加權(quán)局部密度自適應(yīng)的流形距離核”,表示為: (17) 該核函數(shù)得到的距離空間是離散值,區(qū)間為[0,+∞],相似度空間區(qū)間為[0,+∞]。通過(guò)式(17),可知該函數(shù)滿(mǎn)足以下基本性質(zhì): 1) 非負(fù)性:Kij≥0; 2) 自反性:Kij=0; 3) 對(duì)稱(chēng)性:Kij=Kji; 4) 一致性:當(dāng)S(xa,xb) ASC-MDK在樣本充分時(shí),可通過(guò)考慮數(shù)據(jù)聚類(lèi)的全局分布,局部復(fù)雜分布情況,進(jìn)行自適應(yīng)調(diào)節(jié)。但當(dāng)數(shù)據(jù)匱乏時(shí),該方法依然不會(huì)得到理想效果,由此引入遷移學(xué)習(xí)解決這個(gè)問(wèn)題。基于F-范數(shù)的正則項(xiàng)遷移譜聚類(lèi)方法(TSC-IDFR)[21]在SC算法上,引入遷移學(xué)習(xí)機(jī)制形成了基于高級(jí)知識(shí)遷移的譜聚類(lèi)算法,即把源域提取出的高級(jí)知識(shí)進(jìn)行遷移,指導(dǎo)目標(biāo)域數(shù)據(jù)集的聚類(lèi)。 TSC-IDFR通過(guò)減小目標(biāo)域數(shù)據(jù)和源域數(shù)據(jù)上的知識(shí)之間的不相似程度,得優(yōu)化函數(shù)為: (18) 式中:U(C)和U(O)分別表示目標(biāo)域數(shù)據(jù)和源域數(shù)據(jù)的特征矩陣;KU(C)和KU(O)分別表示U(C)和U(O)對(duì)應(yīng)的相似度矩陣。經(jīng)過(guò)變換,得到優(yōu)化目標(biāo)函數(shù): (19) 式(19)通過(guò)最小化目標(biāo)函數(shù),即最大化tr(U(C)U(C)TU(O)U(O)T),作為遷移正則項(xiàng)加入譜聚類(lèi)原始優(yōu)化函數(shù)中,那么TSC-IDFR的最優(yōu)化模型為: (20) s.t.U(C)TU(C)=I 經(jīng)變換得: (21) s.t.U(C)TU(C)=I 式中:λ為調(diào)整目標(biāo)域關(guān)于源域知識(shí)的遷移程度,其參考取值范圍為(0.1,1.0)。 在該遷移譜聚類(lèi)方法基礎(chǔ)上,融入ASC-MDK算法,提出基于流形距離核的自適應(yīng)遷移譜聚類(lèi)算法(ATSC-MDK),其最優(yōu)化模型為: (22) 輸入:源域數(shù)據(jù)集data(O),目標(biāo)域數(shù)據(jù)集data(C),聚類(lèi)個(gè)數(shù)c,伸縮因子ρ,最近鄰點(diǎn)數(shù)k 輸出:目標(biāo)域數(shù)據(jù)點(diǎn)的劃分c1,c2,…,ck 步驟1使用第K近鄰機(jī)制為輸入的目標(biāo)域數(shù)據(jù)集data(C)從源域數(shù)據(jù)集data(O)中挑選可參照樣本集(采用網(wǎng)格搜索方法)。 (1) 通過(guò)迪杰特斯拉算法[25]進(jìn)行數(shù)據(jù)集任意相鄰兩點(diǎn)最短路徑選擇,并通過(guò)式(8)計(jì)算最短路徑和。 (2) 根據(jù)式(12)、式(13)計(jì)算參數(shù)σi和σj。 (3) 根據(jù)共享近鄰算法計(jì)算SNN(xi,xj)+1;最后計(jì)算式(17)得到Kij。 (4) 計(jì)算數(shù)據(jù)集的拉普拉斯矩陣L,其中: 對(duì)角元素為:Kii=0,1≤i,j 構(gòu)造拉普拉斯矩陣:L=D-K。 算法流程圖如圖4所示。 圖4 ATSC-MDK算法流程圖 3.1.1 相似度對(duì)比分析 相似度矩陣對(duì)于譜聚類(lèi)算法進(jìn)行特征提取而言是至關(guān)重要的一步,會(huì)直接影響聚類(lèi)結(jié)果。如圖5所示,以雙月型數(shù)據(jù)集(如圖3所示)為例,(a)為以本文提出的距離核計(jì)算的相似度矩陣,(b)為傳統(tǒng)譜聚類(lèi)的高斯核計(jì)算的相似度矩陣。以高斯核計(jì)算的距離矩陣類(lèi)別分布不明顯,無(wú)明顯規(guī)律可循,說(shuō)明以歐氏距離計(jì)算的相似度矩陣很大程度上忽略復(fù)雜數(shù)據(jù)集的分布結(jié)構(gòu),而本文距離核計(jì)算的點(diǎn)陣顏色分布及深淺較明顯,呈塊對(duì)角模式,可看到明顯分類(lèi)。這表明,本文方法能更好地反映數(shù)據(jù)集的內(nèi)在結(jié)構(gòu)和整體分布,采用的流形距離測(cè)度較空間分布形狀不敏感,更能考慮流形分布對(duì)聚類(lèi)的影響。且通過(guò)考慮邊緣密度情況,降低邊緣密度影響造成錯(cuò)分情況。最后采用加權(quán)自適應(yīng)核參數(shù),避免了參數(shù)敏感,且降低了噪聲點(diǎn)的干擾。 (a) 距離核 (b) 高斯核圖5 兩種方法相似度矩陣計(jì)算對(duì)比 3.1.2 復(fù)雜度分析 本文算法主要執(zhí)行任務(wù)是計(jì)算ATSC-MDK算法的迭代過(guò)程。ATSC-MDK運(yùn)行一次需要分別進(jìn)行源域和目標(biāo)域的ASC-MDK算法。選取來(lái)自源域的樣本數(shù)據(jù)時(shí)間復(fù)雜度是O(m×n2),利用Dijkstra算法搜索最短路徑的空間復(fù)雜度為O(n2),構(gòu)建KNN網(wǎng)絡(luò)并賦權(quán)的計(jì)算徑向基參數(shù)時(shí)間復(fù)雜度為O(n2),SNN共享近鄰時(shí)間復(fù)雜度O(n2),調(diào)整系數(shù)λ時(shí)間復(fù)雜度O(n),本文整體迭代次數(shù)為T(mén),因此算法的時(shí)間復(fù)雜度為O(m×n2+3n2+n)。本文所提算法處理數(shù)據(jù)量較大時(shí),可利用GPU對(duì)算法進(jìn)行加速,增加算法的實(shí)用性。 為驗(yàn)證ATSC-MDK算法的有效性,將使用三組人工模擬數(shù)據(jù)集和三組公共數(shù)據(jù)集進(jìn)行實(shí)驗(yàn)對(duì)比。本文除了與SC算法比較,還將與ASC-MDK、FCM、TI-KT-CM、TII-KT-CM、TSC-IDFR算法進(jìn)行對(duì)比。 實(shí)驗(yàn)采用歸一化互信息(NMI)和蘭德指數(shù)(RI)[26]兩大常用方法作為評(píng)價(jià)標(biāo)準(zhǔn)。 (23) 式中:P(i,j)為同時(shí)聚類(lèi)到U類(lèi)和類(lèi)標(biāo)簽為V的概率,P(i)為聚類(lèi)到U類(lèi)的概率,P′(j)為聚類(lèi)到V類(lèi)的概率。NMI取值范圍為[0,1],越趨近于1,聚類(lèi)效果越好。 (24) 實(shí)驗(yàn)環(huán)境:所用PC為Xeon處理器,2.8 GHz,16 GB RAM, 算法編程使用MATLAB2016a。 3.2.1 模擬數(shù)據(jù)集及實(shí)驗(yàn) 遷移學(xué)習(xí)的場(chǎng)景要求領(lǐng)域相關(guān)且不相同,為此本文在以下場(chǎng)景進(jìn)行實(shí)驗(yàn): (1) 高斯分布遷移數(shù)據(jù)集M1-M2:如圖6所示的低維人工模擬數(shù)據(jù)集。(a)為采用高斯概率分布函數(shù)隨機(jī)生成4類(lèi)共800個(gè)數(shù)據(jù)樣本的源域數(shù)據(jù)集;(b)-(h)為采用高斯概率分布函數(shù)隨機(jī)生成4類(lèi)320個(gè)數(shù)據(jù)樣本的目標(biāo)域數(shù)據(jù)集。 圖6 高斯分布遷移數(shù)據(jù)集M1-M2 (2) 雙月型遷移數(shù)據(jù)集L1-L2:如圖7所示,(a)不含噪聲,共121個(gè)數(shù)據(jù)點(diǎn)且分為上下兩類(lèi);(b)-(h)為受噪聲干擾,共120個(gè)數(shù)據(jù)點(diǎn)且上下分類(lèi)界限有重疊,邊緣分布較復(fù)雜。 圖7 雙月型遷移數(shù)據(jù)集L1-L2 (3) Threecircles遷移數(shù)據(jù)集C1-C2:如圖8所示,(a)為三個(gè)同心圓圍起來(lái)的源域數(shù)據(jù)集;(b)-(h)為非同心圓,且有交叉的目標(biāo)域數(shù)據(jù)集。 圖8 Threecircles遷移數(shù)據(jù)集C1-C2 由圖6-圖8和表1可得:SC算法在人工數(shù)據(jù)集上表現(xiàn)效果較差,ATSK-MDK算法在兩大評(píng)價(jià)指標(biāo)上均高于其余對(duì)比算法,可以得到較好的聚類(lèi)效果。 表1 人工模擬數(shù)據(jù)集的各類(lèi)算法聚類(lèi)效果對(duì)比 M1-M2:凸形數(shù)據(jù)集中,ATSC-MDK,TSK-IDFR是在SC算法基礎(chǔ)上進(jìn)行知識(shí)遷移,TI-KT-CM和TII-KT-CM是在FCM算法上進(jìn)行知識(shí)遷移,經(jīng)過(guò)表1數(shù)據(jù)聚類(lèi)結(jié)果對(duì)比,均在原始算法上有所提升,說(shuō)明在場(chǎng)景遷移中,來(lái)自源域的歷史信息可以進(jìn)行有效的遷移,提高目標(biāo)域聚類(lèi)效果。 L1-L2:L1為絕對(duì)流形數(shù)據(jù)集,L2目標(biāo)域數(shù)據(jù)集為數(shù)據(jù)分布較分散,數(shù)據(jù)相互重疊的流形數(shù)據(jù)集,邊緣數(shù)據(jù)分布較復(fù)雜,容易造成錯(cuò)誤聚類(lèi),且為典型的非凸型數(shù)據(jù)集。在考慮數(shù)據(jù)流形分布的情況下,可充分體現(xiàn)流形距離優(yōu)勢(shì)。基于FCM下進(jìn)行知識(shí)遷移的TI-KT-CM和TII-KT-CM很明顯對(duì)于非凸形數(shù)據(jù)集聚類(lèi)效果不佳,但效果依舊有所提升,進(jìn)一步說(shuō)明遷移學(xué)習(xí)的有效性。而SC算法可以適應(yīng)任意形狀的數(shù)據(jù)且不易陷入局部最優(yōu),所以對(duì)于非凸形數(shù)據(jù)集有明顯優(yōu)勢(shì)。在此基礎(chǔ)上,考慮到這種特殊的流形分布,ASC-MDK明顯優(yōu)于歐氏距離的SC,加入流形距離的ATSC-MDK算法明顯優(yōu)于歐氏距離的TSC-IDFR算法。且根據(jù)實(shí)驗(yàn)結(jié)果,在此種分布下,考慮數(shù)據(jù)的分布結(jié)構(gòu)比加入遷移學(xué)習(xí)方法提升效果更為突出。 C1-C2:FCM是通過(guò)尋找聚類(lèi)中心的方法進(jìn)行聚類(lèi),在此種多流形分布下,聚類(lèi)中心非常難找,沒(méi)考慮分布結(jié)構(gòu)的情況下,聚類(lèi)錯(cuò)誤率非常高,正確率不超過(guò)30%,所以隸屬度進(jìn)行遷移的TI-KT-CM,TII-KT-CM算法,提升效果微乎其微。此種形狀的數(shù)據(jù)集,SC算法的優(yōu)勢(shì)非常明顯,ASC-MDK算法可以更進(jìn)一步考慮分布的全局一致性,面對(duì)復(fù)雜邊緣分布,且可自適應(yīng)調(diào)節(jié),效果有所提升。ATSC-MDK針對(duì)以上問(wèn)題,面對(duì)分布結(jié)構(gòu),邊緣密度等復(fù)雜情況,聚類(lèi)效果較好。 3.2.2 真實(shí)數(shù)據(jù)集實(shí)驗(yàn)結(jié)果分析 為了進(jìn)一步驗(yàn)證算法的有效性,在三個(gè)公共數(shù)據(jù)集上驗(yàn)證,該數(shù)據(jù)集為遷移學(xué)習(xí)、聚類(lèi)效果常用的驗(yàn)證數(shù)據(jù)集,具有一定的基準(zhǔn)性。 (1) 數(shù)據(jù)集1:來(lái)自UCI的人類(lèi)活動(dòng)時(shí)間序列數(shù)據(jù)集。從中選取來(lái)自志愿者的6類(lèi)自然活動(dòng):走路,上樓梯,下樓梯,坐下,站立,躺下。本文源域選取494條女性數(shù)據(jù)記錄,目標(biāo)域選取312條男性數(shù)據(jù)記錄,并進(jìn)行降維處理。 (2) 數(shù)據(jù)集2:來(lái)自ESF數(shù)據(jù)庫(kù)的垃圾郵件數(shù)據(jù)集。本文源域使用公共消息資源的4 000條數(shù)據(jù)記錄,目標(biāo)域使用用戶(hù)的1 800條數(shù)據(jù)。 (3) 數(shù)據(jù)集3:來(lái)自Brodatz紋理數(shù)據(jù)庫(kù)。圖9為源域紋理圖像,圖10為目標(biāo)域紋理圖像(有噪聲)。通過(guò)濾波方法對(duì)紋理特征進(jìn)行提取,且對(duì)維度進(jìn)行處理,構(gòu)成了最終TIS紋理數(shù)據(jù)。 圖9 源域 圖10 目標(biāo)域 真實(shí)遷移場(chǎng)景數(shù)據(jù)與真實(shí)數(shù)據(jù)集的各類(lèi)算法聚類(lèi)效果對(duì)比如表2、表3所示。 表2 真實(shí)遷移場(chǎng)景數(shù)據(jù) 表3 真實(shí)數(shù)據(jù)集的各類(lèi)算法聚類(lèi)效果對(duì)比 由表2和3可得:ATSC-MDK算法在NMI和RI指標(biāo)中均高于其余算法,雖然在人類(lèi)活動(dòng)序列數(shù)據(jù)集中,提高不太明顯,但是在垃圾郵件數(shù)據(jù)集中提高比較明顯,所以總體聚類(lèi)效果有所提升。在考慮到數(shù)據(jù)的空間分布時(shí),ASC-MDK在經(jīng)典譜聚類(lèi)的基礎(chǔ)上對(duì)核函數(shù)機(jī)型改進(jìn),對(duì)比SC效果有明顯的提升,說(shuō)明考慮空間分布可以較好地提高聚類(lèi)效果。TSC-IDFR中融合ASC-MDK所建立的ATSC-MDK算法,克服數(shù)據(jù)數(shù)量影響聚類(lèi)性能的問(wèn)題,對(duì)比SC聚類(lèi)效果有很大提升。 真實(shí)目標(biāo)域數(shù)據(jù)集與源域數(shù)據(jù)集分布相似但不相同,在分布時(shí)有一定的差異性,所以ATSC-MDK、TSC-IDFR、TI-KT-CM、TII-KT-CM均可獲得來(lái)自源域的有用信息,提高目標(biāo)域的聚類(lèi)有效性。ATSC-MDK不僅選取有用數(shù)據(jù)集,考慮源域和目標(biāo)域的空間分布特征,因此選取最有效的指導(dǎo)目標(biāo)域的數(shù)據(jù)集,在一定程度上有效避免了負(fù)遷移。 為提高SC算法的領(lǐng)域適應(yīng)能力,降低數(shù)據(jù)空間分布、樣本數(shù)量等對(duì)其性能的影響,本文提出一種基于流形距離核的自適應(yīng)遷移譜聚類(lèi)算法(ATSC-MDK)。考慮數(shù)據(jù)分布的全局一致性,使用流形距離作為相似性計(jì)算方法,充分考慮全部局部鄰域信息,對(duì)核函數(shù)進(jìn)行自適應(yīng)調(diào)整,提高譜聚類(lèi)對(duì)復(fù)雜數(shù)據(jù)集的處理能力;考慮領(lǐng)域數(shù)據(jù)匱乏問(wèn)題,引入遷移學(xué)習(xí),使用源域的知識(shí)輔助目標(biāo)域進(jìn)行譜聚類(lèi)。實(shí)驗(yàn)結(jié)果表明,本文算法性能與原始譜聚類(lèi)算法相比有明顯提升。2 算法設(shè)計(jì)
2.1 基于流形距離核的自適應(yīng)譜聚類(lèi)算法(ASC-MDK)


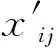
2.2 ATSC-MDK算法
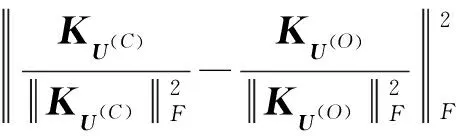
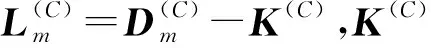
2.3 算法流程
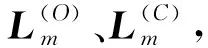
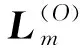
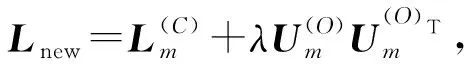

3 實(shí) 驗(yàn)
3.1 算法分析

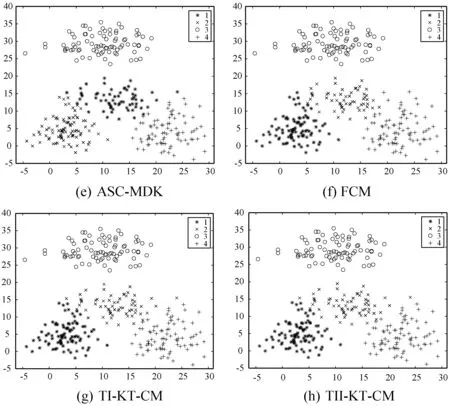
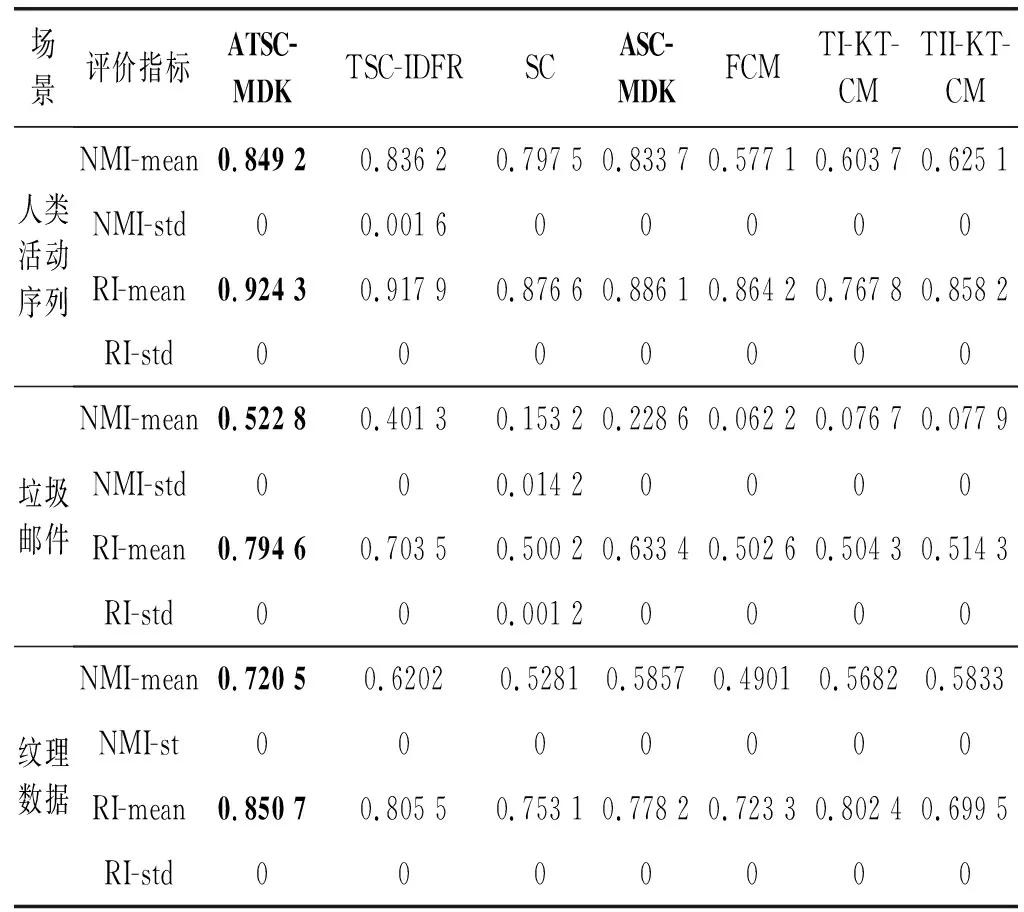
3.2 算法對(duì)比






4 結(jié) 語(yǔ)

