云環境保護競價隱私的最佳路徑算法

王 超 張 磊* 張春玲

1(佳木斯大學信息電子技術學院 黑龍江 佳木斯 154007)2(牡丹江技師學院 黑龍江 牡丹江 157000)

0 引 言

隨著云技術的發展尤其是基于位置服務以及導航的廣泛應用[1]，最佳路徑選擇已成為人們日常出行、外出旅游的首選服務[2-3]。與最短路徑不同，通常情況下，最佳路徑指用戶在固定區間內可在最短時間或最佳體驗效果的情況下到達指定目的地的移動路徑[4-5]。雖然在很多情況下最佳路徑就是最短路徑，但是仍存在較大概率最短路徑并不能滿足用戶的最佳體驗。因此，相對于最短路徑的計算，最佳路徑處理計算更為復雜，但云技術的發展為最佳路徑的計算帶來了便捷。在云環境下，最佳路徑計算一般由不同用戶提供移動路徑競價，同時經過云環境比較并給予一定補償后獲得。因此，在競價過程中，為云環境提供最佳路徑信息的用戶更加關心自己提供的信息尤其是競價信息是否安全。針對云環境處理最佳路徑隱私的問題，Zhang等[6]就考慮過受限最佳路徑的云環境處理，并利用同態加密技術對用戶信息加密實現了對最佳路徑信息的隱私保護。Xi等[7]也通過使用PIR(Private Information Retrieval)方法實現了導航最佳路徑競價數據的隱私保護。Aivodji等[8]更是提出使用多方安全計算實現多用戶同時最佳路徑計算并保障多用戶競價隱私的處理方法。但是，當前對于競價的隱私保護手段一般使用加密技術，并通過競價多方與云之間的信息交互來實現競價比較[9-10]，雖然能夠有效地保護競價隱私，但通常會由于加密處理以及密態環境下的比較導致處理效率相對較低，且很難實現多輪競價。針對效率和多輪競價問題，閆小勇等[11]提出最佳路徑搜索的二進制協議，該方法雖然能夠提升效率卻又無法有效保護競價隱私。因此，本文基于二進制前綴族提出一種可包含用戶競價隱私的云環境下的最佳路徑算法。利用二進制前綴碼建立前綴族，并通過對前綴族使用哈希加密的方法建立保密環境下的比較集合，然后將該集合提交給云環境，并由云環境比較后獲得最佳路徑。整個計算比較過程中，一方面由于使用的是前綴族，使得云環境無法在該族群內準確地識別用戶提交的最佳路徑競價，另一方面由于前綴族使用哈希加密，其他競價用戶即使獲得競價信息也無法獲知用戶的真實競價。同時，本文算法在處理效率上要優于同類的多方安全計算方法，既可以支持多輪競價，又不需要在用戶和云之間重復多次計算，因此其時間效率要優于現有的多方安全計算方法。

1 最佳路徑競價和前綴族

1.1 最佳路徑競價

通常情況下，云環境下的最佳路徑比較可看作是一種通過云環境實現的多方競價的網絡拍賣過程，即通過由云環境提供的物質激勵對協作用戶提交的最佳路徑進行競價[9]，競價獲勝者能夠獲得物質獎勵。與網絡競拍不同的是，該過程是經過比較獲得競價最低值，即最佳路徑取值。因此，這種競價過程可表示為如圖1所示的最低競價比較過程。

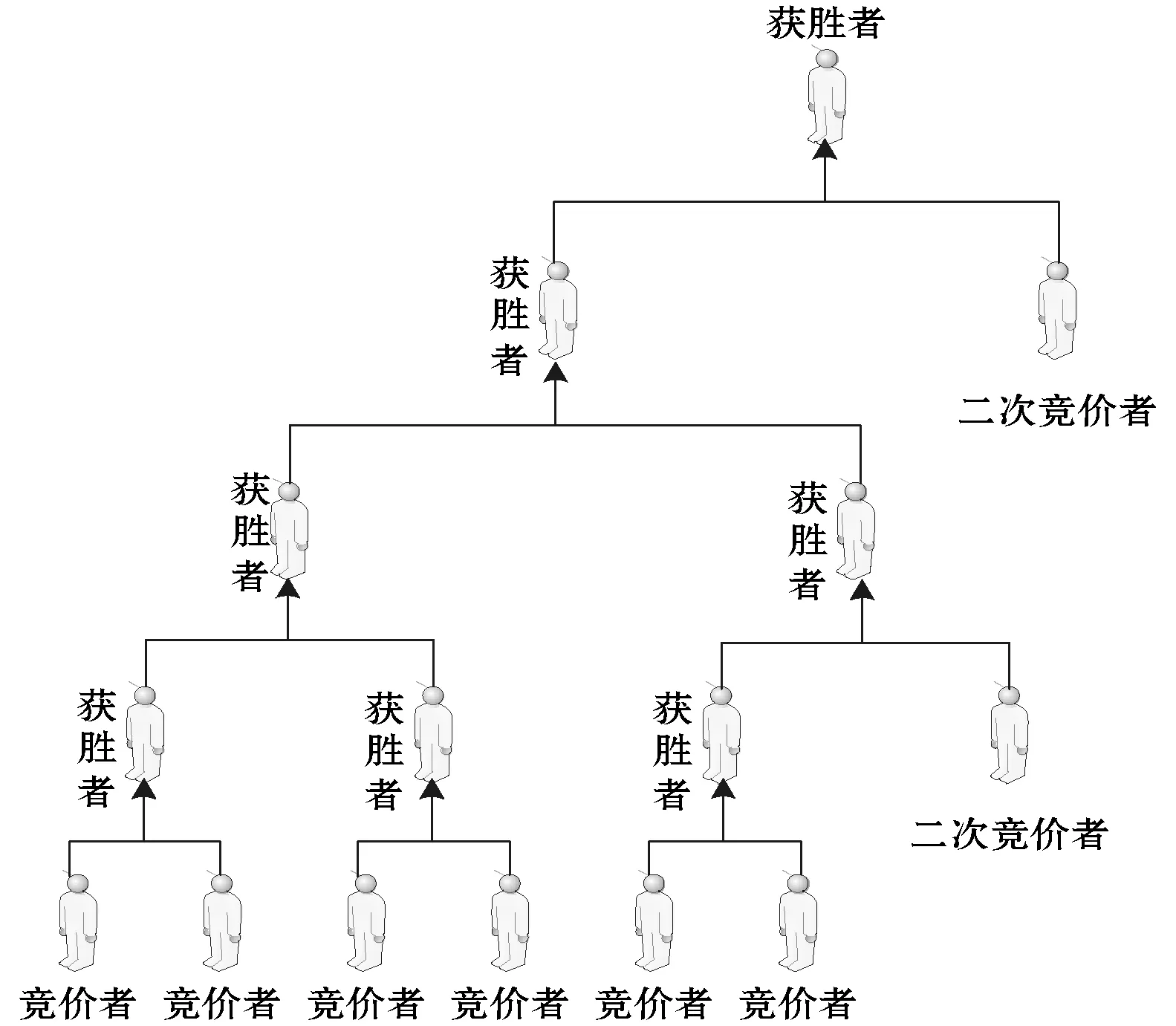
圖1 云環境最佳路徑的競價過程

可以看出，在云環境下競價者之間不僅存在一次競價比較，還存在當前出價失敗之后的二次競價甚至三次競價，直到不存在最佳路徑競價才能獲得最后的競價結果。因此，這種最佳路徑競價是一種多輪競價方式，故基于加密技術實現的隱私保護單輪競價方式無法滿足需要。同時，由于在競價的過程中，任何競價者都不希望其競爭者獲知其競價數值，因此還需在多輪競價中保持用戶競價隱私。

1.2 前綴族

前綴族是通過交運算來驗證某一數值是否在被判定的某一區間范圍內，即通過交運算來檢測數值范圍[12]。對于s-前綴族{0，1}s{*}w-s有s個0或者1，以及s個(w-s)*s，其中*可用0或者1來替代。例如：1***表示1-前綴族，而11*表示2-前綴族。由此，一個s-前綴族可代表一個從{0,1}s{0}w-s到{0,1}s{1}w-s之間的數值范圍。例如：p=1****表示的范圍是[10 000,11 111]，也就意味著一個數值滿足s-前綴族當且僅當具有相同首位的s位二進制數與s-前綴族相同。假設存在w比特長度的二進制數x=b1,b2,…,bw，則關于x的前綴族可表示為F(x)={b1,b2,…,bw,b1,b2,…,bw-1*,…,b1*…*,*…*}，該前綴族有(w+1)個元素，其中第i個可表示為b1,b2,…,bw-1+i*…*。例如數字9的二進制表示是01001，則F(9)={01001,0100*,010**,01***,0****,*****}，于是有對于一個給定的數值x以及前綴p，x位于p范圍內當且僅當p∈F(x)。其中，前綴族的范圍[d1,d2]可表示為P([d1,d2])，該范圍包含多個前綴，每個前綴覆蓋范圍[d1,d2]中的一個子范圍，并且所有前綴覆蓋整個前綴族的范圍[d1,d2]。例如，p([7,25])={001111,011110,111100,111000,110000,1****}，所以，x∈[d1,d2]當且僅當F(x)∩P([d1,d2])≠?。因此可利用前綴族這一特性制定一種隱私保護的競拍策略，一方面防止同類競價者獲得競價隱私信息，另一方面能夠實現多輪競價。基于這一思想，本文提出一種基于前綴族的隱私保護競價的最佳路徑算法，并以此實現隱私保護的多輪競價。

2 基于前綴族的隱私保護競價

2.1 隱私競價處理

使用前綴族的隱私保護競價可以簡單地劃分為兩個階段：第一階段為最佳路徑競價的前綴族編碼，第二階段為最佳路徑多輪競價秘密比較。為了進一步增強算法的隱私保護能力，將最佳路徑競價使用哈希加密增強競價的保密性。因此，競價的處理可按照前綴族編碼和多輪競價秘密比較展開。

最佳路徑競價前綴族編碼階段：

第1步云平臺發布指定起始點位置區域最佳路徑任務，同時給出最佳路徑的最高競價；

第2步各競價者在收到競價任務后，將自己的競價按照前綴族進行編碼，并同時將自己的競價與最高競價合并建立競價區間；

第3步各競價者使用哈希函數對前綴族和競價區間進行加密，并獲得加密后的信息H(F(x))和H(P([d1,d2]))并發送給云平臺。

最佳路徑多輪競價秘密比較階段：

第1步云平臺將收到的由各個競價者發送的哈希值按照前綴族和競價區間加以區分；

第2步平臺執行算法1對前綴族和競價區間加以比較并獲得當前最佳路徑取值；

第3步云平臺發布當前競價勝者，并同時接收第二輪競價前綴族和競價區間；

第4步重復執行第2、3步，直到無后續競價。

算法1前綴族最佳路徑競價比較

輸入：接收到的n個競價者發送來的哈希加密后的前綴族集合Hi(F(x))和競價區間集合Hi(P([d1,d2]))，1≤i≤n,k=n。

輸出：最低競價結果前綴族min(H(F(x)))。

1. for(i=1;i<=n;i++)

2. for(j=1;j<=n;j++)

3. if(Hj(F(x))∩Hi(P([d1,d2]))≠?)

//判斷集合交集

4.k=k-1;

//計算元素重合次數，即交集出現次數

5. end if

6. if(k<2)

7. min(H(F(x)))=Hi(F(x));

//獲得最佳路徑競價

8. else

9. 算法執行失敗；

10. end if

11. end

12. end

上述過程可表示為前綴族與競價區間中每個子項之間的相交關系。例如：假設云環境提出的當前最佳路徑競價的最高值為25，存在4個競價者向云環境提出競價，且分別是2、3、5、6，則按照前綴族編碼將得到表1所示的競價前綴族和競價區間。

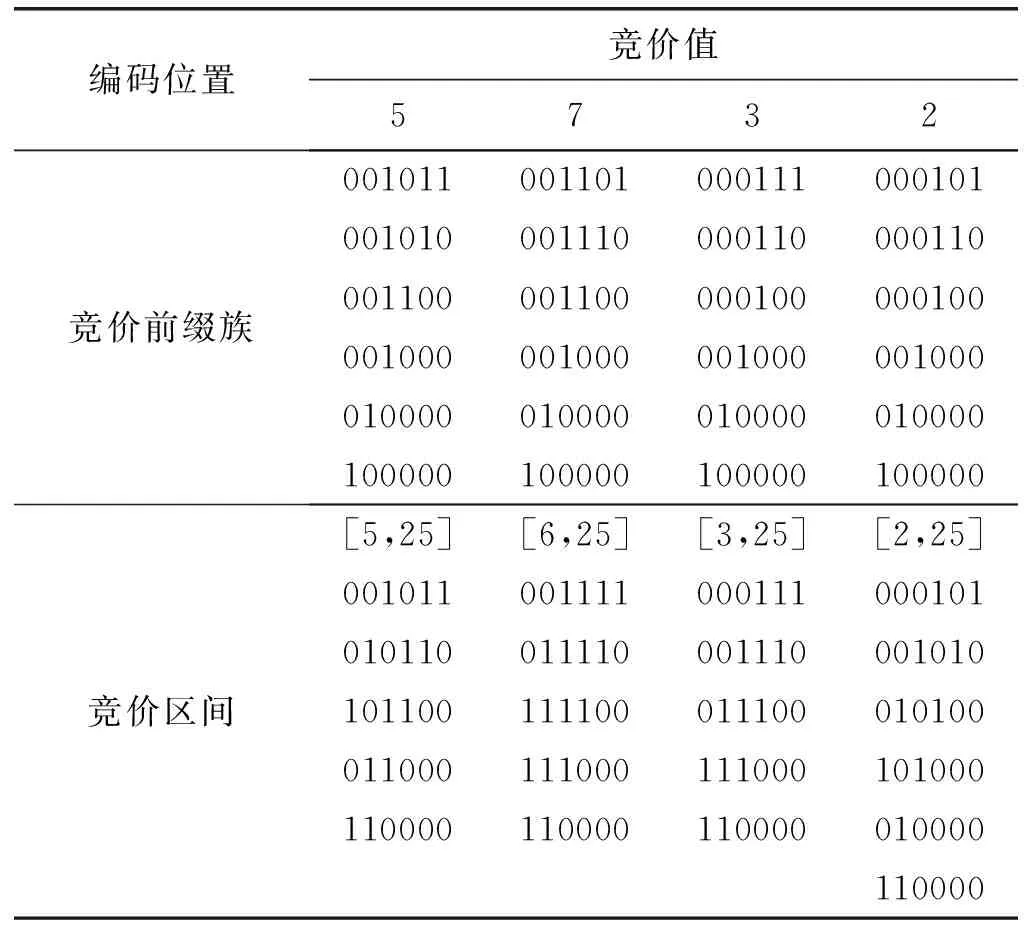
表1 前綴族的競價編碼

可以看出，[2,25]這樣的競價區間與包含在該區間內的所有競價之間的交集都不為空，則該區間為包含最佳路徑區間。此時與該區間同時提交的競價為最佳路徑競價。同時，對應于使用哈希函數加密后的集合中的每個元素，由于哈希算法的抗碰撞性上述元素交集計算成立，且由于哈希加密的單向性，上述競價不會被包括云環境在內的各個競價實體所獲知，競價隱私得到了保護。

2.2 安全性分析

使用前綴族在云環境下比較獲得最佳路徑競價的安全性取決于包括云環境在內的各個實體無法準確地獲知競價者出價。本文算法將競價內容轉換為前綴族，使得單一競價被擴展為一組至少由6個二進制數組成的前綴族，同類競價用戶即使通過搭線等攻擊手段獲得該族，也只能得到k個近似二進制競價，準確獲知用戶的真實競價的比例為1/k。在競價過程中，用戶利用哈希函數對前綴族中的每一個二進制數進行加密，而由于哈希函數的單向加密和抗碰撞特性，使得包括云服務器在內的整個參與競價的實體均無法對所獲得的競價信息加以解密，進一步保障競價信息的隱秘性。整個競價的比較過程是通過利用H(F(x))和H(P([d1,d2]))進行交運算結果是否為空的比較獲得最佳競價的，整個過程中不需要進行任何的實際價值對比，同時也不似同態加密那樣進行密態環境下的數值計算。因此無論云環境是否具有極強的計算能力以及信息分析能力，均無法猜測獲得競價信息，進一步保障整個競價處理過程中的信息隱蔽性，提高了最佳路徑競價比較的安全性。

3 實驗驗證

為驗證本文算法在執行過程中的計算效率以及算法在多輪隱私競價方面的隱私保護能力，本文在Windows 10環境下，使用Core i7處理器，8 GB內存的筆記本電腦利用MATLAB 2017a進行模擬驗證。參與比較的算法有基于編碼和加密的RADP算法[12]、使用同態加密進行比價的PPSP算法[6]、基于差分隱私的TATP算法[10]以及基于加密的CMQN算法[9]。實驗將在算法執行時間、最高同價競價比較次數、競價信息不確定性以及加密競價的可猜測概率等方面展開比較。

圖2給出了不同算法在隨競價人數增加的情況下算法的執行時間差異。可以看出，所有算法的執行時間均隨著競價人數的增加而增加，這是由于各算法需要對每個競價進行比較。本文算法的執行時間最短，這是由于本文算法僅需進行集合交集運算，而不需要數值比較。TATP算法采用添加噪聲的方法，需要同時對噪聲數據進行數值比較，執行時間稍高。CMQN算法對加密數值進行比較，其比較過程需要解密后才能完成，因而其執行時間高于CMQN算法。RADP算法雖然也使用集合，但是其編碼效率要低于本文算法，而且需要進行密文比較而不是集合交集運算，因此其執行時間同樣高于本文算法。PPSP算法采用基于同態加密的多方安全計算方式，需要在競價用戶與云服務器之間多次進行秘密計算，算法執行時間最高。

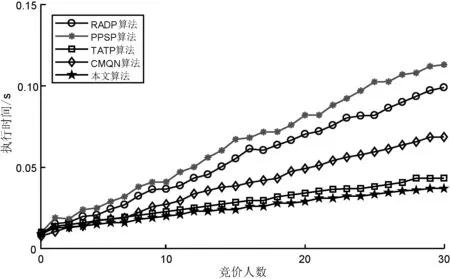
圖2 算法執行時間

圖3給出了出現相同最高競價情況下，不同算法對相同最高競價的處理輪次。對于相同最高競價，一般的處理方法是需要競價用戶重新進行出價，并再次進行競價比較。從圖3中可以看出，本文算法的比較次數最低，這是由于在相同競價產生之后本文算法僅需對再次競價用戶進行競價比較，不需要與其他已完成競價的用戶比較。RADP算法與本文算法相類似，但是需要在最后的比較中與前次比較的次優用戶進行比較，因此比較次數要高于本文算法。CMQN算法采用加密實現隱私競價，但其主要針對的是單次競價，在重新競價時需要與所有用戶進行比較。TATP算法與CMQN算法類似，但是由于添加的噪聲同樣需要加以比較，因此其比較次數高于CMQN算法。PPSP算法采用基于同態加密的多方安全計算，其比較不僅需要對所有競價重新進行秘密比較，還需要進行每個用戶間的隱私競價比較，因此最高同價競價比較次數最多。

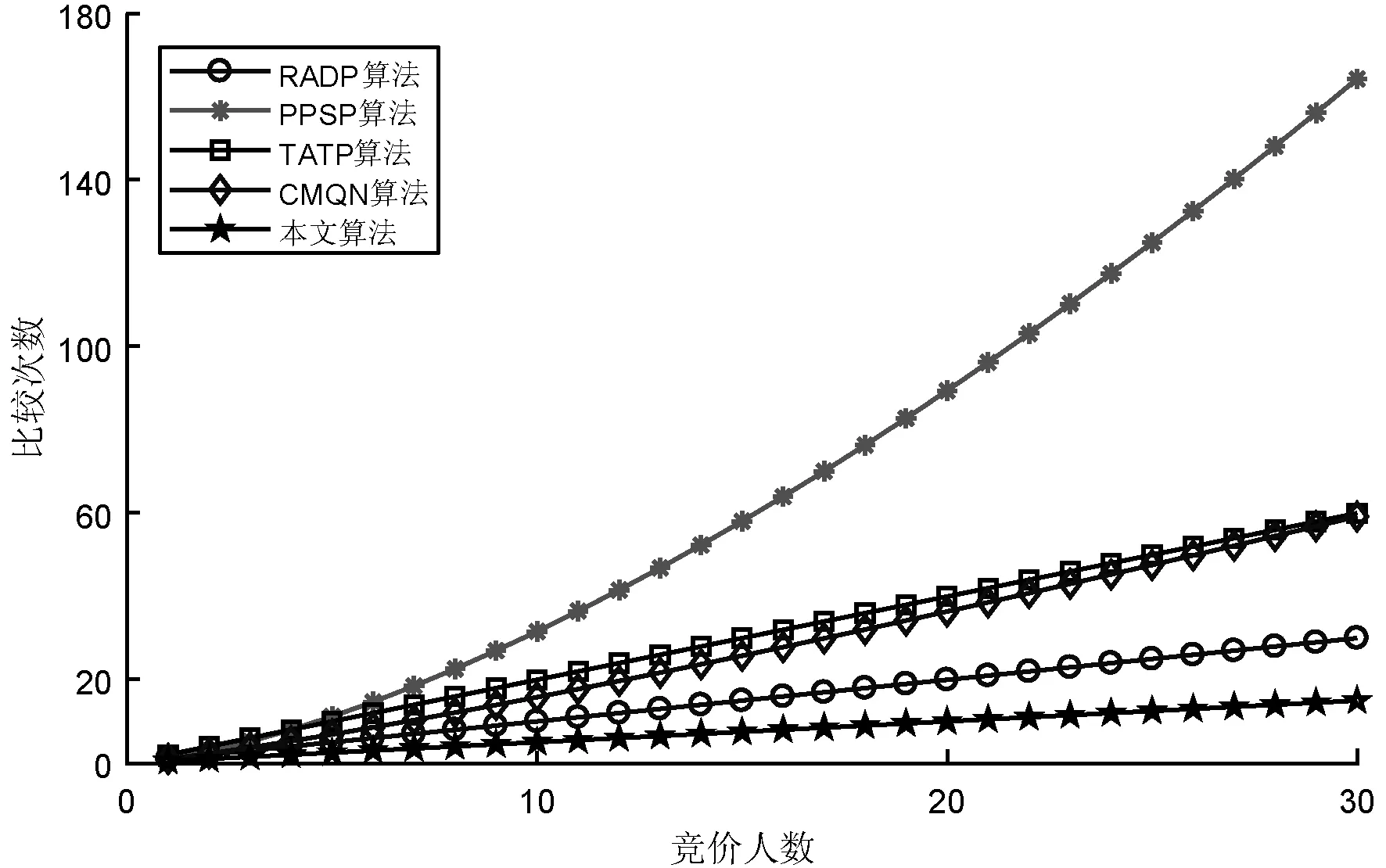
圖3 最高同價競價比較

圖4給出了競價用戶提交競價所組成的競價集合中真實競價的不確定性。可以看出，隨著競價人數的增加，本文算法、RADP算法和TATP算法的不確定性都隨之增加，而PPSP算法和CMQN算法卻未產生變化。這主要是因為CMQN算法使用加密處理，其信息不確定性并不受競價人數影響，且始終保持競價的單一加密性。PPSP算法盡管也是采用加密手段，但是由于同態加密的同態特性，其秘密計算是在競價用戶之間進行，所以其信息不確定性要高于CMQN算法。TATP算法通過噪聲實現隱私比較，其競價信息不確定性隨用戶增加而增大。RADP算法采用競價分組模式，其競價分組數量隨競價人數增加而增加，因而具有更高的不確定性。本文算法不僅采用競價分組模式，而且分組數量隨著競價值位數的變化而增加，因而具有最高的不確定性。

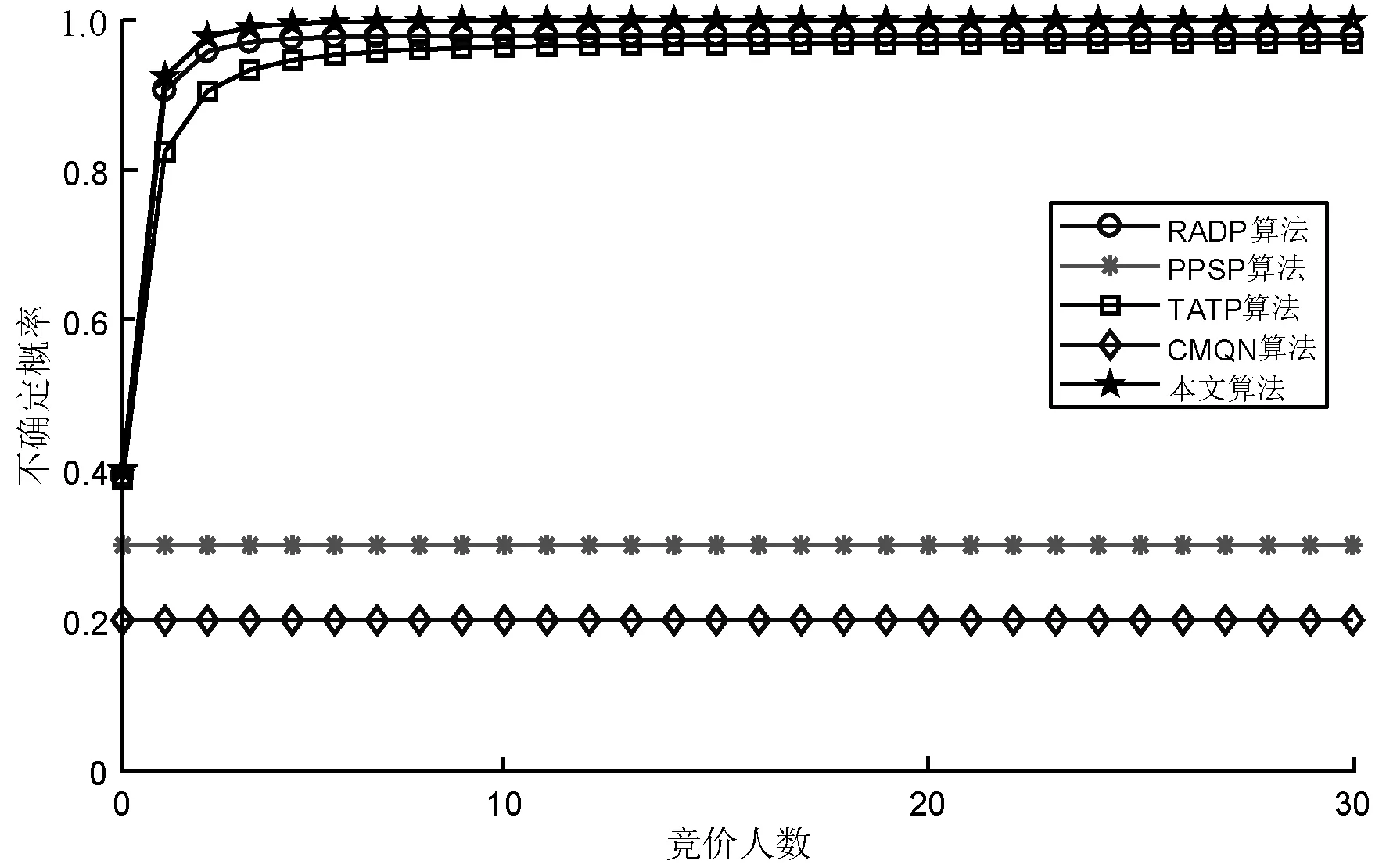
圖4 競價信息不確定性

圖5給出了云環境在強計算能力下，對加密的用戶競價成功猜測的成功概率。可以看出，隨著競價人數的增加，云環境對競價成功用戶的猜測成功率逐漸降低。但是，TATP算法由于只是簡單地添加了噪聲競價，因而其猜測成功率要高于其他算法。CMQN算法僅對競價進行單一加密，這使得其猜測成功率雖然低于TATP算法但仍然很高。PPSP算法采用多方安全計算，在共謀的情況下其競價隱私存在一定的被識別概率，因而其猜測成功率要高于RADP算法和本文算法。RADP算法采用分組后加密比較的方式實現隱私競價比較，但是其分組數量有限，影響了該算法的隱私保護能力，因而其加密競價的可猜測概率高于本文算法。本文算法一方面使用哈希加密后的集合交集運算，增加了競價信息的隱私比較特性，另一方面隨著競價值位數的變化增加當前競價分組數，進一步增加了競價信息的不確定性，可猜測概率最低。

圖5 加密競價可猜測概率

4 結 語

為了保障在云環境處理下對用戶最佳路徑的隱私競價給予保護，本文提出一種基于二進制前綴族的云環境下保護競價隱私的最佳路徑算法。一方面將用戶競價轉換為泛化后的前綴族二進制編碼，令攻擊者無法準確識別；另一方面，將這種前綴族利用哈希函數加密為單向不可逆的加密編碼，進一步加大對競價的保護。同時，由于采用前綴族與競價區間加密值交運算比較的方式獲得最佳路徑，整個計算處理過程并沒有受上述處理影響而增加計算復雜度和處理負載，因此具有較好的執行效率。通過與其他同類算法在隱私保護能力與算法執行效率兩個方面的比較結果也可看出，本文算法具有更好的適用性。然而，本文算法僅可用于最佳路徑的競價計算過程，仍無法解決云環境其他計算處理的隱私問題，今后的研究工作將在云環境數據隱私保護以及數據隱私利用等方面展開。