“理解算理”的測試維度與水平分析

王來波 王敏烽 鄭娟娟

【摘? ?要】理解算理是運算能力的重要表現(xiàn)特征。“理解算理”測評可以從算理表述的正確性、算理表征的層次性、算理遷移的通用性三個維度展開，并對其進行水平劃分與分析。通過區(qū)域測評發(fā)現(xiàn)，“20以內進位加法”在理解算理維度上，呈現(xiàn)算理表征層次性不強、算理遷移通用性水平不高等特點。

【關鍵詞】理解算理;水平分析;20以內進位加法

一、算理的含義和理解表現(xiàn)形式

算理和算法是計算教學中相輔相成、缺一不可的兩個方面。理解算理是運算能力的重要表現(xiàn)特征。算理的表現(xiàn)形式主要有：運算的意義、十進制與位值制思想、運算的性質與定律、運算之間的互逆關系。

“20以內進位加法”重點掌握“湊十法”，算理的表現(xiàn)形式是“運算的意義”“十進制”“運算的性質”。以“9+4”為例，運算的意義是“要把9和4合并起來”;十進制是“拆分湊十的過程”;運算的性質是“依據(jù)加法結合律先湊十，再十加幾”。因為湊十法是后續(xù)整數(shù)進位加法的主要算法，其背后的算理也是后續(xù)進位加法的主要算理。所以，“20以內進位加法”是加法算理的一節(jié)種子課。

二、“理解算理”的測試維度與樣例說明

對“理解算理”的檢測，主要通過各種題型的測試暴露學生算法背后思考的過程，并進行算理理解的水平劃分。“理解算理”的測試，可以圍繞 “算理表述的正確性”“算理表征的層次性”“算理遷移的通用性”三個維度展開。

（一）“算理表述的正確性”檢測樣例與水平劃分

算理表述的正確性主要反映為圖式的一致性，通過讓學生根據(jù)算法來選擇圖示，檢測算理與算法的一致性。

“20以內進位加法”中的算法主要依托框架式來呈現(xiàn)，展現(xiàn)算法的過程;而算理主要依托直觀圖示或文字來解釋算法背后的道理。如“8+9”的口算，可以有兩種拆分湊十的方法，學生要找到與此對應的圖示，理解“湊十法”背后的“十進制”（如表1）。

（二）“算理表征的層次性”檢測樣例與水平劃分

算理表征的層次性主要采用不同的物化材料來表征算理的檢測方式，如文字、符號、圖形等，不同的表征方式反映出對算理的理解水平。

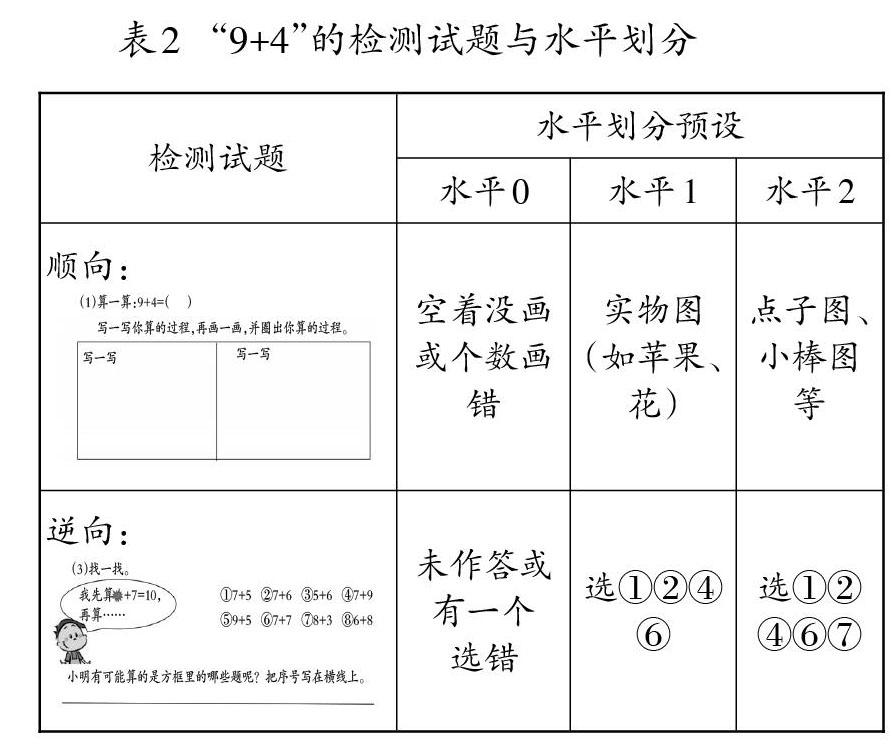
如，“9+4”的算理表征檢測，可以讓學生根據(jù)“9+4”算的過程，畫一畫、圈一圈，把想法表示出來;也可以讓學生根據(jù)算的局部過程，還原算式。通過順向、逆向的試題檢測，完成“湊十法”背后算理理解水平的劃分（如表2）。

（三）“算理遷移的通用性”檢測樣例與水平劃分

算理遷移的通用性，主要采用未學先試的檢測方式，考查學生能否將同一算理自主遷移到后續(xù)學習內容中，從而反映學生對算理的理解程度。

“20以內進位加法”后續(xù)學習內容是“兩位數(shù)加一位數(shù)的進位加法”，共通的算理是“十進制”。可以仿照“9+4”的順向測試題進行編制，如“根據(jù)19+4算的過程，畫一畫、圈一圈，把想法表示出來”，完成算理遷移通用性水平的考查（如表3）。

會算的同學，請你把19+4算的過程寫一寫、畫一畫。][寫一寫][畫一畫] 空著沒畫或個數(shù)畫錯 實物圖 點子圖、小棒圖，體現(xiàn)十進制位值制 ]

三、“20以內進位加法”理解算理水平區(qū)域調查分析

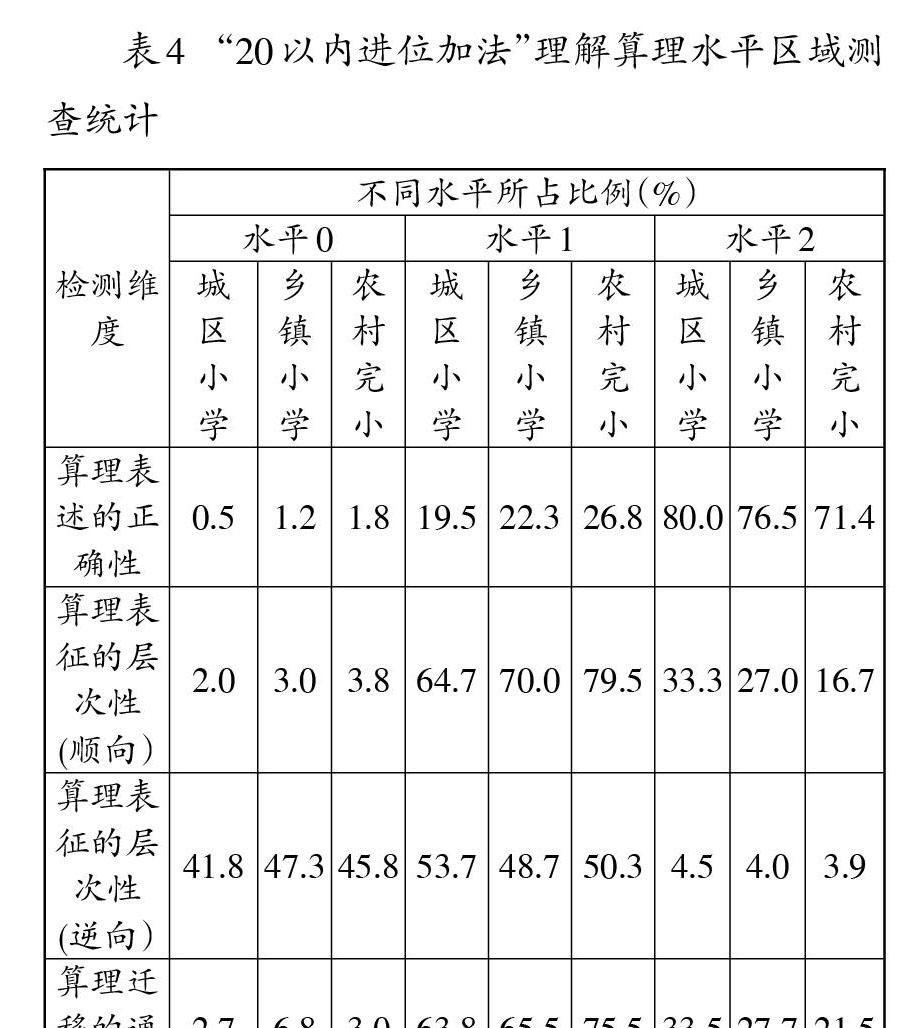
“20以內進位加法”理解算理水平區(qū)域測查，選取城區(qū)小學、鄉(xiāng)鎮(zhèn)小學和農村完小各5所，每所學校2個班級，共計1200名學生參加測查。檢測維度包括算理表述的正確性、順向和逆向的算理表征的層次性、算理遷移的通用性，每個維度劃分為三個水平，對每個群體的每個水平比例進行統(tǒng)計分析，具體數(shù)據(jù)如表4所示。

從表4可以發(fā)現(xiàn)，區(qū)域“20以內進位加法”理解算理能力水平呈現(xiàn)三個特點。一是算理表征表述的正確性總體水平較高，城鄉(xiāng)差異不大;二是算理表征的層次性總體水平偏低，順向表征能力略高于逆向表征能力;三是算理遷移的通用性明顯受算理表征的層次性的影響，水平等級的人數(shù)分布和算理表征的層次性（順向）非常接近。

（一）算理表征的層次性不明顯，材料缺乏結構性

算理表征物化手段統(tǒng)計顯示，有60%左右的學生選用實物圖，如蘋果、花朵等;有30%左右的學生選用點子圖;只有5%左右的學生選用小棒圖。另外，還有5%的學生用文字、寫算式等。其中有一所農村完小全班都畫了蘋果圖。

點子圖、小棒圖和實物圖都屬于表征算理的物化材料。物化材料主要分為齊性材料和結構性材料，像點子圖、小棒圖和實物圖都屬于齊性材料，計數(shù)器、數(shù)位筒等屬于結構性材料。測查數(shù)據(jù)說明，“20以內進位加法”教學中大量使用的是齊性材料，表征方式較為單一，教師應有意識滲透結構性材料，讓學生盡早感知十進制位值制。當然，算理表征除了層次性之外，還要做好順向、逆向表征的融會貫通，以更好地理解算理。

（二）算理點狀教學，導致算理遷移的通用性水平較低

“十進制位值制”是“20以內進位加法”非常重要的算理之一，基于這一算理，才有了湊十法。“9+4”表征算理的過程性，大部分學生的作品如圖1、圖2所示，畫圖只是點數(shù)出結果，或從運算意義的角度畫出“9+4”的意義，沒有體現(xiàn)十進制思想。正因為“20以內進位加法”的十進制思想教學的缺失，導致“19+4”算理表征的時候十進制思想也沒有體現(xiàn)，學生只是畫出算式的意義或排成一列點數(shù)出結果（如圖3），很少有學生有“圈十”的過程。

在“20以內進位加法”的教學中，位值制思想雖然不是這節(jié)課的重點，但對后續(xù)學習有一定影響。教學中，只需借助直觀圖或計數(shù)器簡單滲透即可。從學生的作品反映來看，多數(shù)教師缺乏整體思考，算理的點狀教學是導致算理遷移的通用性水平低的主要原因。

總之，無論是教學，還是測評，都需要高度重視算理。通過“算理表述的正確性”“算理表征的層次性”和“算理遷移的通用性”三個維度的測評，可以讓算理更加顯性化，從而提升學生的運算能力。