面向計算思維能力培養的STEM+C教育案例探究
——以“基于SIR模型的疾病傳播模擬”活動為例

曹曉靚

（中國福利會少年宮）

一、STEM教育和少兒編程教育教學實施現狀

（一）發現問題

1. 本土化的優質STEM教育課程缺乏

2017年發布的《中國STEAM教育發展報告》指出，目前國內的STEM課程還存在著諸多“水土不服”：STEM教學體系和評價缺乏系統化規范；相關教學資源的配置與使用在設計并實施一個STEM課程中至關重要，硬件設施和材料在開展課程時的損耗較高，這導致了STEM課程經費負擔重、課程更新慢；目前還呈現出學科整合不到位、相關經驗遷移難、資源共享難、師資嚴重缺乏等問題。通過文獻研究和教學實踐總結，發現能夠真正做到“跨學科”和“真落實”的本土化優質STEM課程并不多[1]。

2.少兒編程教育多注重技術忽視探究

近年來，隨著人工智能的發展，少兒編程教育的浪潮席卷全球。2017年中國國務院印發的《新一代人工智能發展規劃》中也明確提出應逐步在中小學推廣編程教育[2]。由此可見，青少年編程教育的普及是目前迫切需要的。雖然近年來計算思維的培養開始依托編程教育逐漸蓬勃發展起來，但通過研究者們的調查發現，大多發生在校內信息技術課堂上的編程教育內容都側重編程語法和算法構建，卻往往忽視了在探究學習中培養學生創新素養和跨學科解決真實問題的能力。

（二）SWOT分析法

20世紀80年代初，由美國舊金山大學的管理學教授韋里克提出的SWOT分析法常被用于競爭對手分析和企業戰略制定等場合，它是基于矩陣圖思維框架的一種分析方法。主要截取組織發展的四個維度：優勢（S）、劣勢（W）、機會（O）、威脅（T），然后通過歸納、對比和概括對組織狀況進行系統分析[3]。筆者主要采取文獻研究法，運用SWOT分析的原理，從四個維度對國內STEM教育一線教學實施現狀進行了分析和總結，使得培養計算思維的STEM+C（Computing）課程開發設計更具科學化。

（三）基于國內STEM教育一線教學實施現狀的SWOT矩陣

由于圖形化編程語言成本低、易于線上推廣、遠程培訓教師，以圖形化編程語言為輔助技術支持的STEM+C（Computing）課程能夠大大降低STEM教育的學習門檻；同時可以做到上下延伸，良好銜接，上接圖形化語言、STEAM多元化資源，下接開源開發板、物聯網硬件；融入機器學習、圖像識別等人工智能技術后也提升并開闊了STEM課程內容的高度與寬度，在學生思維的過渡期，可以起到很好的銜接作用。另一方面STEM的融合也有助于彌補現有編程課程體系中跨學科解決真實問題的能力和創新素質培養上的不足。

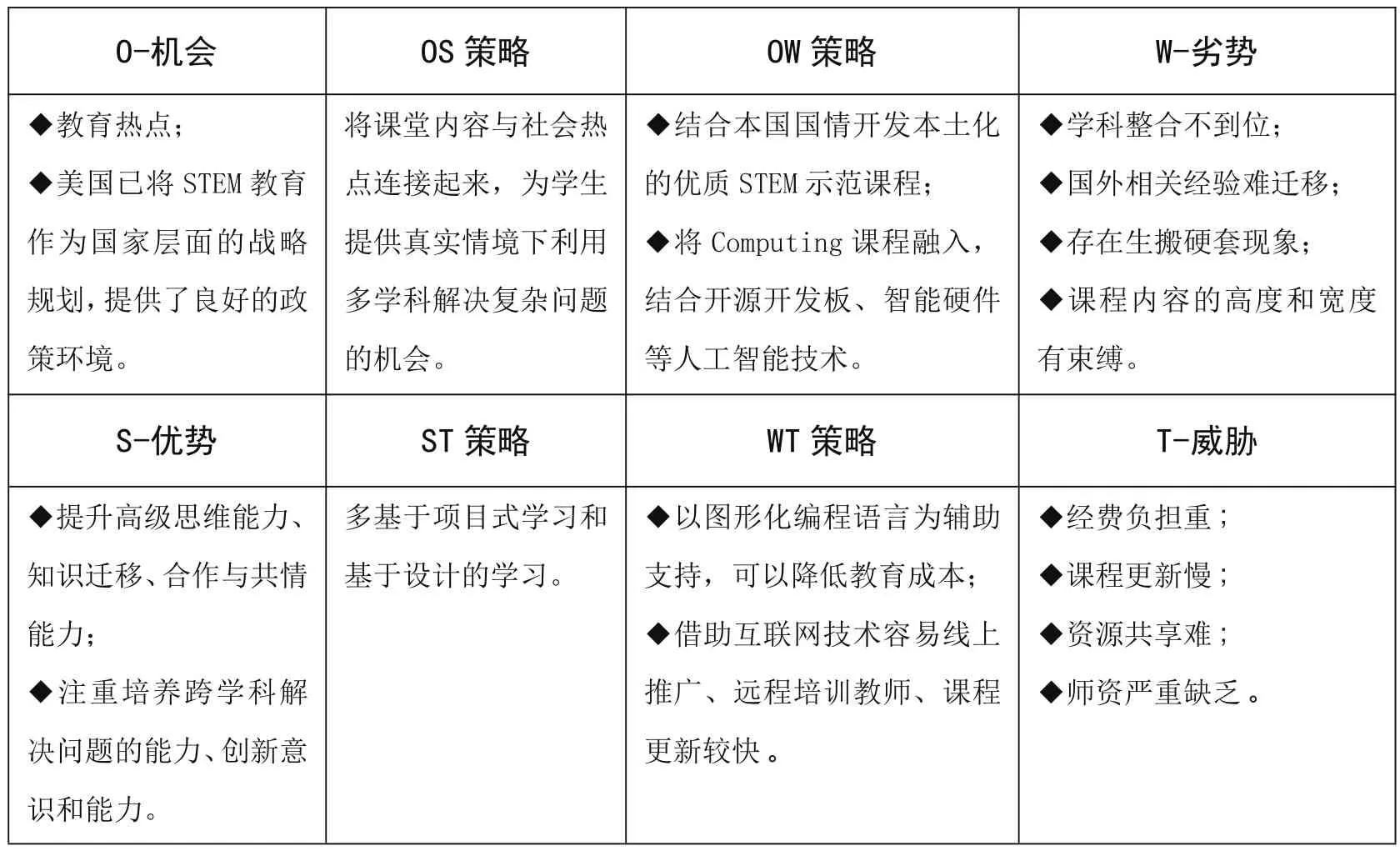
表1 基于國內STEM教育一線教學實施現狀的SWOT分析表

計算思維強調要基于真實問題展開，充分利用計算機科學的概念和方法解決真實情境中存在的問題。與之相似的一點，STEM教育同樣是注重通過多學科知識和多元化工具去解決真實情境中的復雜問題。因此，開發面向計算思維能力培養的STEM+C(computing計算)課程是極具現實意義和研究價值的。

二、基于STEM+C活動的計算思維培養模型設計

有國外學者提出，計算思維的包含“分解（Decomposition）、抽象（Abstraction）、算法 （Algorithms）、調試（Debugging）、迭代（Iteration） 和歸納（Generalization）”六個要素[4]。STEM課程注重探究、學科整合與真實情境的交互。在設計相關課程時，應培養學生獨自探究與合作探究的能力。探究過程要注重課程之間的銜接性，調動學生的興趣和求知欲，促使學習者自主發現并學會解決問題。設置層次分明的遞進式任務，步步深入發展學生的高級思維，同時做好相關拓展課程的延伸和知識遷移。在設計課程時，應注重多學科間的深入整合，情境的創設與支持也應從雙向考量，從真實情境中的問題出發再回歸到真實情境中去。根據這些特點，筆者構建了如圖1所示的基于STEM+C活動的計算思維培養模型。

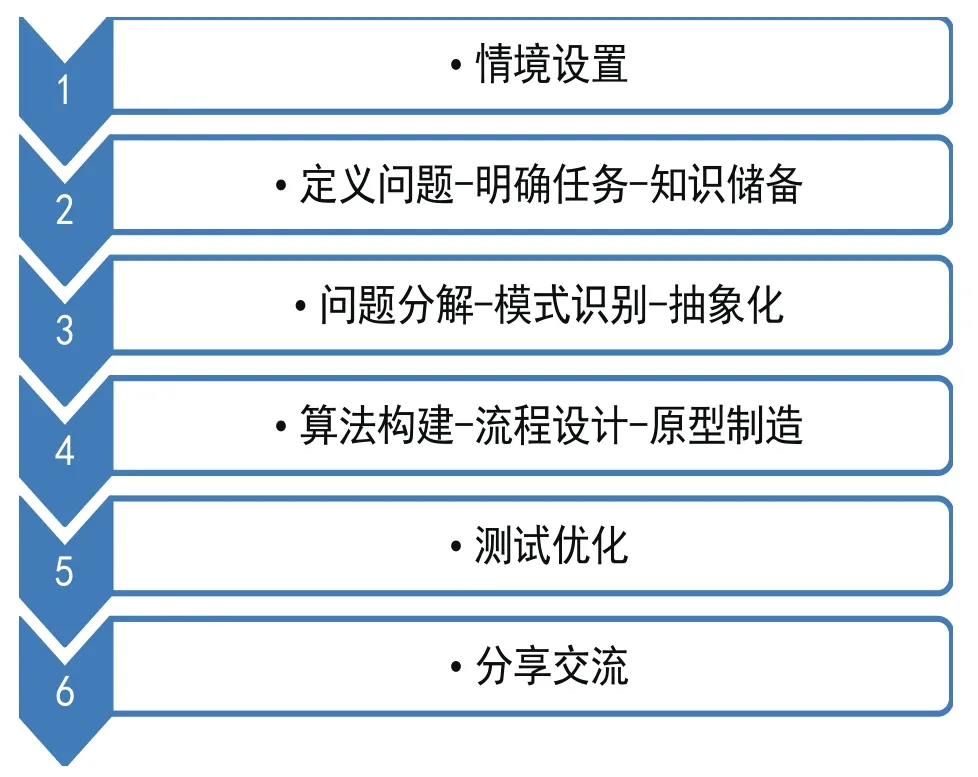
圖1 基于STEM+C活動的計算思維培養模型

三、教學案例剖析

下面通過對“基于SIR模型的疾病傳播模擬”活動案例的分析，具體闡述上述模型的應用。活動中將利用計算思維的方式重新解構科學課的一些具體問題，以此掌握計算思維解決真實問題的方法和能力。

第一步：情境設置，激發興趣

2020年新冠肺炎爆發，中國工程院院士鐘南山早前曾預測南方地區2月中旬將會達到發病最高峰。那么，科學家是如何預測的呢？

第二步：定義問題，明確任務，知識儲備

鐘南山院士對疫情的預測并不是憑借經驗，而是通過數學模型分析并結合實際情況作出的判斷。下邊我們就闡述如何一步步認識疾病傳播的過程，從簡單到復雜，建立起疾病傳播模型，最后用圖形化編程語言來實現疾病傳播的模擬。

知識儲備1—— 基本傳染數

通常記做R0，它是指在沒有外力介入，同時所有人都沒有免疫力的情況下，一個感染者會把疾病傳染給多少人的平均數[5]。R0的數目愈大，代表流行病的控制愈難，取決于當時各種環境因素，比如是否密閉空間、病患的癥狀和攜帶病毒的指數等。

知識儲備2 —— SIR模型

經典的“易感者-感染者-免疫者”傳染病模型，又叫SIR模型，像水痘、天花等疾病都遵循SIR模型，是指得了一次病就不會再得第二次。但有些疾病感染上之后可能下次還會患，就像我們最常見的感冒和流感，不會獲得免疫力，它稱之為“易感者-傳染者-易感者”模型（SIS模型）。

第三步：問題分解-模式識別-抽象化

1.問題分解——化繁為簡，各個擊破

計算思維的第一個步驟是把復雜的問題分解成若干易于處理的小問題。我們可以將疾控中的人群分成三大類：易感者（S）、感染者（I）、免疫者（R）。

2.模式識別——分析辨認，厘清關系

構建出它們的關系模型：易感者→感染者→免疫者。

3.抽象化——聯系舊識，模式歸納

定義“鄰居”：把每個人抽象成一個方塊，每個與方塊任意一邊相鄰的方塊“鄰居”代表的是社交圈里的一個人，假設每個人有4個鄰居。

定義“一格”：現實生活中從傳染、生病到治愈都需要一定的時間，我們假設將這段時間周期稱之為“1格”。

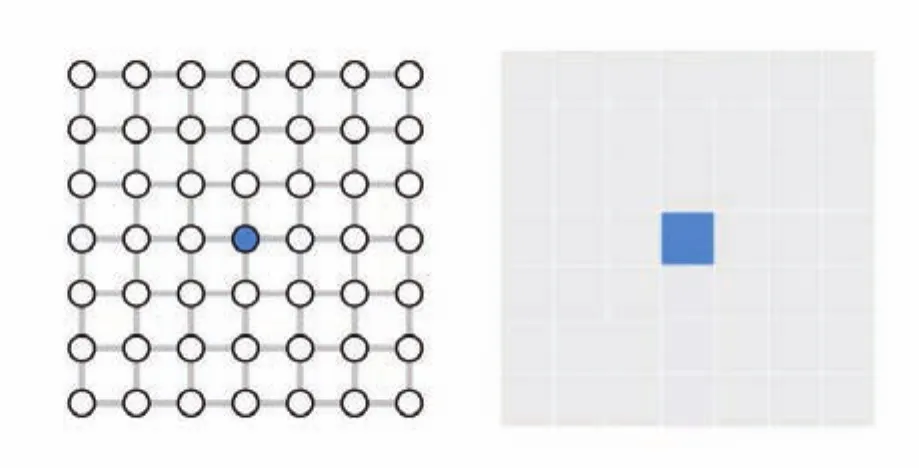
圖2 抽象化

第四步：算法構建-流程設計-原型制造

1.算法開發——設定規則，制造解決

所謂算法，就是指模型運行的規則。

規則1：感染者有一定概率在下一步讓易感者鄰居成為感染者。

規則2：疾病只能通過感染者傳播給“鄰居”，而不能隔空傳播。

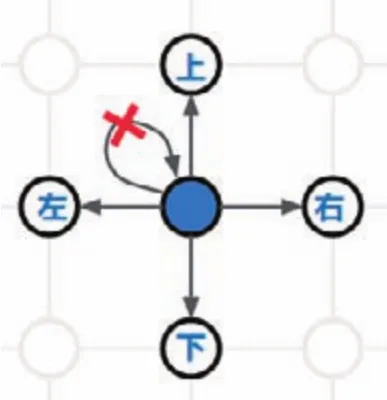
圖3 算法規則

2.流程設計

學生可以通過思維導圖的方式進行數據流分析，梳理每個角色之間的結構關系和事件關系。

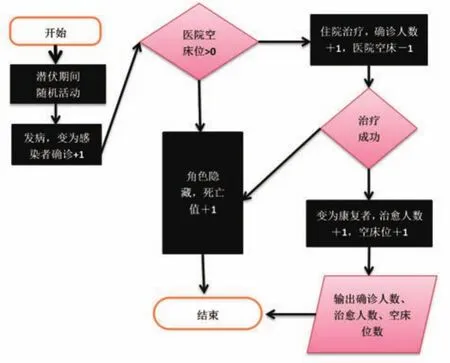
圖4 “傳染源”角色的流程圖

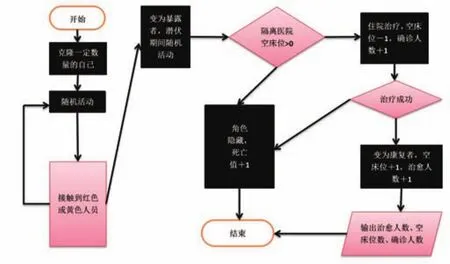
圖5 “易感者”角色的流程圖

3.編寫程序

隨著一號病源的活動，陸陸續續有接觸者被感染，從綠色變為黃色，然后發病轉為紅色，在有床位的情況下感染者被送往醫院隔離治療，但隨著病毒大面積爆發，右上角的死亡病例數值逐漸攀升，到了后期治療成功的藍色康復者越來越多。這個治愈概率該如何表示呢？可以用隨機數來解決這個問題！如果假設治愈率為70%，在1到100的數值范圍內隨機返回一個數值，而隨機返回值大于30的概率有70%。

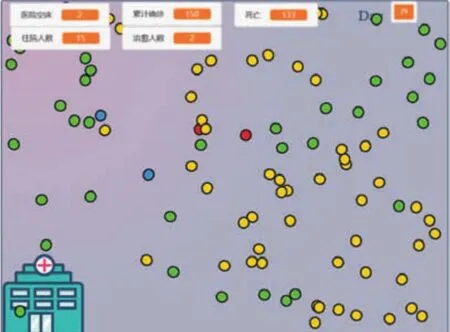
圖6 場景設置

第五步：測試優化

接下來我們可以通過修改模擬規則增加挑戰，讓它更接近真實生活。

1.現實生活中，幾乎不存在傳染率為100%的疾病，大多數疾病是易感者接觸了感染者后，有一定概率中招成為感染者，這就是我們前面說的傳染率。可以將感染率設置為一個變量，在模型中通過拖動滑桿改變感染的概率。

2.如果是SIS模型下，又要改變哪些規則呢？

第六步：分享交流

1.請用自己的話描述一下基本傳染數的概念。

2.除此之外，我們還可以用模擬驗證一下戴口罩的意義，自己試試看吧！

四、總結與反思

這種運用計算機科學的基礎概念去求解問題、設計系統和理解人類行為的思維模式就是計算思維[6]。此次是筆者STEM+C教育的案例探究，樂于與大家共享和探討不足之處。STEM教育融入C（Computing）課程，是以信息化技術為抓手、基于項目式學習的方式，運用科學原理、數學計算、工程設計培養學生計算思維的有效手段。計算思維并不一定要通過編程來實現，它不是計算機的思維，而強調的是人的思想，所以它不能直接與編程思維畫等號。計算思維的思想是要教會學生如何組織、分析，并且高效地解決生活或學習中的真實問題。所以建議教師力圖將課堂與社會熱點連接，提供解決真實情境中有效問題的機會，引導學生學會思考和分析己有方案的優缺點，簡化、優化算法，逐步找到最優解決方案。學習再多的理論，都需要經過實踐和不斷反思，希望在過程中找到自己的不足，探索更好的教學方法，設計更利于學生計算思維發展的活動內容。