基于OpenFOAM平臺的鈍體穩焰器尾流動力學分析①
王 祎,吳寶元
(1.液體火箭發動機技術重點實驗室 西安航天動力研究所,西安 710100;2.航天推進技術研究院,西安 710100)
0 引言
由于固體沖壓發動機燃燒室等多種吸氣式發動機燃燒室入口來流流速遠高于火焰傳播速度,在不采取任何措施的情況下無法組織穩定燃燒,因此需要采用合理的火焰穩定手段使燃燒室能夠穩定工作[1-2]。
鈍體穩焰器作為一種結構簡單、性能穩定的火焰穩定裝置得到了廣泛應用[3]。其通過在下游產生局部低速尾流形成穩定持續的點燃燒條件,使燃燒室能夠穩定工作。鈍體穩焰器屬于典型的鈍體結構,其流場下游尾流低速區與高速主流之間存在不穩定的剪切層,具有本質非穩定特性[4-6]。同時,鈍體穩焰器尾流流場包含不同尺度的三維非定常渦結構,對流體動力學分析提出了較大的挑戰。
計算流體力學方法(CFD)具備對非定常流場進行精細定量求解的能力,能夠滿足鈍體穩焰器非定常流動研究需求,逐漸成為鈍體穩焰器流動研究的重要方法。從不同的研究目的出發,基于CFD方法的數值研究可大致分為鈍體穩焰器冷態流場研究[7-9]與燃燒場研究[10-11]。這些研究工作均需要以選取合理的湍流模擬方法為基礎獲取合理的鈍體穩焰器非定常尾流流場流動特征。
已有研究結果表明,傳統的雷諾平均湍流模擬方法(RANS)不適用于此類大范圍分離流動問題,需要采用合理的尺度解析湍流模擬方法(SRS)或者大渦模擬方法(LES)[12-13]。另一方面,考慮到壁面直接解析的大渦模擬方法在壁面附近的網格要求與直接模擬方法(DNS)相似,對計算要求較高,壁面模化的大渦模擬方法(WMLES)依然對近壁面網格有較高要求。基于分離渦思想發展而來的DES類方法則充分結合了RANS在近壁面網格處理方面的優勢與LES對自由剪切流動的解析能力,較好的平衡了計算效率與計算精度之間的矛盾,是一種適用于研究鈍體穩焰器尾流流動的湍流模擬方法。
獲取合理的非定常尾流流場計算結果的同時,鈍體穩焰器研究需采用合理的后處理手段對尾流動力學特性進行分析。傳統方法往往通過對鈍體穩焰器升阻力系數或尾流監測點速度壓力等物理量進行快速傅里葉變換獲取動力學特征頻率,但此類方法很難表征整個流場的動力學特征[14]。近年來以本征正交分解方法(POD)[15]以及動力學模態分解方法(DMD)[16]為代表的流場降維分析方法以非定常流場切片為輸入能夠充分考慮整個流場信息,能夠獲取更加豐富的流場動力學特征,是分析鈍體穩焰器尾流非定常流動問題一種很有潛力的方法。
本文選取Sjunnesson等[17]開展的Volvo試驗為基本構型,基于OpenFOAM開源計算力體力學平臺[18],采用改進延遲分離渦湍流模擬方法(IDDES)對其冷態試驗工況進行仿真計算。針對復雜的尾流渦結構,采取Omega渦識別方法對動態渦結構進行識別;進一步采用動力學模態分解方法提取流場主要特征,對尾流流體動力學特性進行詳細分析。
1 計算模型
Volvo流動試驗為Sjunnesson等[17]于1992年公開的的針對鈍體穩焰器開展的試驗研究,具有較詳細的冷熱態試驗結果。試驗結構可以簡化抽象為包含三棱柱鈍體穩焰器的長方體展向流場結構,具體鈍體穩焰器及流場結構尺寸如圖1所示。

圖1 Volvo試驗結構示意圖Fig.1 Volvo rig case configuration
鈍體穩焰器為橫切面為等邊三角形的實心三棱柱結構,另外由上下兩實體面確定流場范圍。展向抽象為無限長,僅截取部分展向長度,并通過周期性邊界進行模化。根據冷態試驗條件可以獲得詳細的計算物理模型邊界條件,見表1。

表1 冷態試驗具體邊界條件Table 1 Cold state boundary conditions
本文采用六面體網格對流場計算域進行網格劃分,對近壁面以及剪切層附近網格局部加密以滿足湍流模擬要求,保證壁面第一層網格特征高度y+<10,同時采用自適應的壁面函數,防止非定常計算過程中局部流場流速變化導致的y+變化。展向包含50層網格,整個計算域共劃分約140萬網格,具體展向橫切面網格如圖2所示。

圖2 展向橫切面網格Fig.2 Grid of the channel plane
參考Sjunnesson等[17]開展的試驗,流場中流體工質為當量比為0.65的丙烷/空氣預混氣體。由于只考慮冷流情況,可將勻混氣體作為符合理想氣體狀態方程的均勻混合物,具體熱物性設置見圖3。

圖3 熱物性具體設置Fig.3 The detailed thermo properties
2 數值模擬方法
2.1 大范圍分離流動模擬方法
本文基于OpenFOAM開源計算流體力學仿真平臺,對Volvo鈍體穩焰器冷態流場進行數值仿真。選取基于κ-ωSST的改進延遲分離渦湍流模型(IDDES)以滿足大范圍分離流動仿真要求。湍流模型具體為
(1)
ρβω2-ρ(F1-1)CDkω+Sω
(2)

(3)
由于湍流粘性由湍流模型提供,因此選取時間空間離散方法時除了保證數值穩定性以外,需要考慮數值粘性,以免得到非物理結果。參考相關文獻,綜合考慮穩定性與數值粘性,空間離散格式選取二階中心有界差分格式,時間離散格式選取二階隱式backward格式。同時選取壓力基PISO迭代方法以進一步減小非定常數值模擬中的數值粘性[20]。選取非定常時間步長為2.0×10-6以滿足CFL數小于1,并選取仿真物理時間為1 s。
2.2 Omega渦識別方法
鈍體穩焰器尾流流場包含復雜的三維渦結構,需選取合理的渦識別方法用于對其進行識別分析。Omega渦識別方法與渦量法以及速度梯度不變量等渦識別方法相比,能夠清晰識別不同強度的渦結構,并且具有較為一致的識別標準[21]。該方法通過定義渦識別變量:
(4)
a=tr(ATA)
(5)
b=tr(BTB)
(6)
式中A,B分別為速度梯度的對稱張量與反對稱張量;ε為一極小值以免出現分母為0,本文選取為0.001;根據相關文獻研究結果,選取Ω=0.52等值面作為渦識別判據。
2.3 動力學模態分解方法[22-24]
動力學模態分解方法(DMD)結合了主成分分析(PCA)與傅里葉變換(FT),可以將含有不同尺度的渦結構分解為不同頻率的主模態,有利于在大量的流場數據中提取主要流體動力學特性進行分析研究。
非定常流場作為一個復雜的非線性動力學系統可以通過線性化為時間離散系統:
xk+1=Axk
(7)
式中 下標表示不同時間步。
選取相同時間間隔的m個瞬態流場結果,基于式(7)可以構建如下動力學關系式:
X=[x1x2…xm-1]
(8)
X′=[x2x3…xm]
(9)
X′≈AX
(10)
可以通過奇異值分解(SVD)方法求得系統矩陣的具體形式:
X≈UΣV*
(11)
A=X′VΣU*
(12)

(13)


(14)
Φ=X′VΣ-1W
(15)
通過對角矩陣Λ中的離散特征值λk可以構建對應的連續特征值ωk=ln(λk)/Δt,其實數部分表征相應DMD模態的增長率,虛數部分表征相應DMD模態的頻率。
定義模態振幅b為不同DMD模態對流場序列X的貢獻,即b=Φ/X。進一步可以使用若干個DMD模態對不同時刻流場進行重構或者預測:
x(t)≈ΦeΩtb
(16)
式中Ω為由特征值ωk組成的對角矩陣。
綜上,采用DMD方法能夠獲得具有主成分特征的DMD模態,相較于傳統的傅里葉分解方法具有更強的可操作性。通過討論其連續特征值的性質能夠辨別各DMD模態的動力學穩定性,并且可以明確不同頻率模態的流動模式,具有較強的物理意義,對于流體動力學分析具有良好的指導意義。
3 計算結果驗證及分析
3.1 計算結果驗證
通過統計物理時間0.5~1.0 s 內時均速度與速度脈動量與試驗結果進行對比,驗證計算結果的準確性。
圖4為選取流場中軸線上軸向時均速度與試驗結果的對比圖。除了給出基于κ-ωSST IDDES湍流模型的計算結果外,也給出了基于κ-ωSST非穩態雷諾平均(URANS)湍流模型的計算結果。通過對比可以明顯看出,基于URANS湍流模型的計算結果與試驗結果相差較大,表明其無法對鈍體穩焰器尾流流場進行較合理地預示。其主要原因是κ-ωSST URANS模型基于線性渦黏假設,其中僅考慮了從大尺度渦向小尺度耗散渦能量級串過程,無法解析自由剪切運動中反向級串過程,導致流場自由剪切部分湍流黏性預示過高,低速回流區含能較大,導致對回流區速度預示過高。IDDES湍流模型在近壁面采用RANS模式能夠配合合理的壁面函數高效的模化附面層流動;在遠離壁面的自由剪切流動切換至適用于自由剪切流的LES模式,對自由剪切流進行合理模化。因此,基于IDDES湍流模型的計算結果與試驗結果較為吻合,速度形預示較為準確。
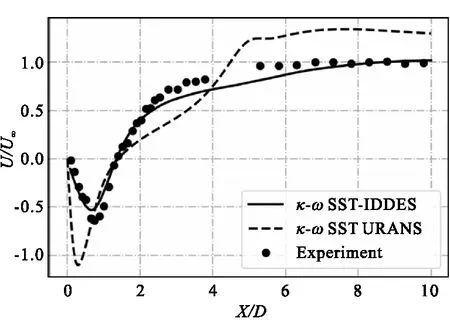
圖4 流場中軸線軸向時均速度形Fig.4 Time-average axial velocity profile along the centerline
為進一步驗證基于IDDES湍流模型計算結果的準確性,圖5與圖6分別給出了沿流場中軸線速度脈動量以及不同流場橫截面上軸向時均速度形的對比示意圖。通過對比分析,表明本文選取求解器、離散格式、流動模型能夠對鈍體穩焰器尾流流場進行較精確地預示。

圖5 流場中軸線速度脈動量分布圖Fig.5 Fluctuation velocity profile along the centerline

圖6 不同流場橫截面軸向時均速度形Fig.6 Time-average axial velocity profile at different cross section
3.2 計算結果分析
在計算過程中對非定常計算結果進行時間平均處理可以獲得相應物理量的時均值與時間脈動量。3.1節已經將時均化的計算結果與試驗結果進行了對比驗證,本節進一步給出軸向時均速度分布圖,如圖7所示。由圖可知,高速來流經過鈍體穩焰器在下游流場形成了典型的尾流結構;與無限大空間鈍體繞流不同的是,由于壁面限制流體在流經鈍體穩焰器的過程中流通面積減小,主流速度明顯高于入口來流速度。

圖7 流場軸向時均速度分布圖Fig.7 Time-average axial velocity profile of flow field
除可通過時均值獲得流場相關物理量的系綜平均結果,相關的脈動量能夠用于表征流場的非定常特性。圖8為流場壓強脈動量分布圖,由計算結果可得,非定常流動主要集中在鈍體穩焰器尾流低速回流區及剪切層部分,且強度沿流向減弱。

圖8 流場壓強脈動量分布圖Fig.8 Pressure fluctuation profile of flow field
在流場中軸線距穩焰器尾緣0.04 m 下游設置觀測點統計其非定常速度值,可通過快速傅里葉變換(FFT)得到單點湍動能隨波數的分布圖,如圖9所示。湍動能分布符合Kolmogorov湍動能 -5/3冪律分布假設[25],同時存在由尾流非定常渦脫落特征頻率為100 Hz左右的分峰值。

圖9 觀測點湍流譜分布圖Fig.9 Turbulence spectrum of the probe point
與時均化結果不同,瞬態流場包含復雜的三維非定常渦結構。由2.2節,選取單個周期不同時刻流場使用Omega渦識別方法進行處理,可以識別尾流流場中復雜的渦結構。
圖10為同一渦脫落周期內不同時刻尾流流場非定常渦結構示意圖。由圖10可知雖然流場具有準二維幾何特征,流體流經鈍體穩焰器除存在典型的非定常卡門渦結構,同時尾流渦存在復雜的三維結構。根據湍流理論,尾流復雜的渦結構是由鈍體穩焰器迎風面湍流附面層發展而來。湍流結構除沿壁面流向及法向二維平面隨時空發展外,同時沿展向發展,最終形成三維流場結構。

圖10 同一周期不同時刻渦結構示意圖Fig.10 Vortex structure of different moment during one periodic time
3.3 流體動力學分析
由3.2節可知,瞬態尾流流場存在復雜的非定常三維渦結構,使用如單點湍流譜等分析方法很難對整個流場進行動力學分析。本節采用DMD方法對非定常流場計算結果進行處理,對流場進行動力學分析。
選取0.05 s內共50個瞬態流場快照采用DMD方法進行處理,截取前45個流場DMD模態及特征值對流場動力學特性進行討論。本文以模態振幅b對DMD模態進行排序,可得不同模態振幅分布,如圖11所示。

圖11 不同DMD模態振幅分布Fig.11 Amplitudes of different DMD modes
根據2.3節,可由離散特征值確定不同DMD模態的穩定性:將復數特征值置于復平面單位圓,若在單位圓內,則相應的DMD模態收斂;在單位圓外,則對應模態發散;在單位圓上,則處于穩定極限環狀態。圖12為對應不同DMD模態的離散特征值在復平面上的分布。由于截取的瞬態流場經過充分發展已經趨于穩定,同時考慮到流場計算過程中的數值粘性因此各模態離散特征值均處于復平面單位圓內。其中,越接近單位圓,其對應模態穩定性越差,當存在相應頻率的流場擾動時相應DMD模態所代表的流動特征越容易被激發為發散狀態。本文選取其中10個接近于單位圓的DMD模態進行討論,如圖10中紅色特征值所示,同時給出其相應的DMD模態編號。其中,不同DMD模態的特征頻率與增長率見表2。由定量數據,除模態5以及模態41以外,其余8個模態為4對共軛模態,10個DMD模態共包含6種不同的特征頻率。

圖12 離散特征值分布Fig.12 Discrete eigenvalues of different DMD modes
可以通過DMD模態流向速度分布確定不同模態對應的具體流動特征。根據對比分析可以得出,其中模態5代表尾流穩定低速區流動,其速度云圖與圖7相似;模態41頻率較高,代表流向/橫向復合流動特性;模態31與39為一對共軛模態,代表剪切層失穩特性,其頻率為剪切層響應頻率;剩余模態特征頻率分別為剪切層響應頻率的1/2,1/4,1/8,即剪切層失穩特性發展成相應的諧波響應流動特性。參照3.2節湍流譜分析結果,卡門渦脫落頻率即為剪切層失穩發展形成,其形式對應于模態18與模態42。
圖13展示了模式5、模式31、模式18三個DMD模態的流向速度分布。三個DMD模態分別表征了穩態尾流流動、開爾文-亥姆霍茲(KH)不穩定流動以及貝納德-馮卡門(BVK)不穩定流動[6]。

表2 不同DMD模態特征頻率與增長率Table 2 Eigenfrequencies and growth rates of different DMD modes

(a) Mode 5

(b) Mode 31

(c) Mode 18圖13 部分DMD模態流向速度分布Fig.13 Axial velocity profile of some DMD modes
由圖13可知,DMD方法能夠獲得具有明確物理意義的流體動力學模態,對于鈍體穩焰器尾流流動特性的討論有很大幫助。
另外,表2所示模態基本位于復平面單位圓上,當存在相應特征頻率的擾動發生耦合時,相應動力學模態隨能量輸入有可能演變為不穩定狀態,因此需規避相應的特征頻率擾動以減小發生流動不穩定的概率。
4 結論
(1)OpenFOAM平臺具備開展鈍體繞流流動計算仿真的能力。選用的κ-ωSST IDDES湍流模型結合合理的離散格式及邊界條件能夠獲得較為準確的流場計算結果。采用該湍流模擬方法能夠兼顧計算效率與計算精度,是一種可用于鈍體穩焰器非定常尾流流場仿真計算的高效方法。
(2)Omega渦識別方法能夠準確直觀展示復雜的渦結構,有助于鈍體穩焰器尾流流場分析;與單流場監測點快速傅里葉變換處理獲得的湍流能譜分析方法相比,DMD方法可以將非定常流場分解為具有不同特征頻率的DMD模態,能夠對尾流流場進行細致的流體動力學分析,有利于從整體上把握流場流動特性。
(3)經由本文分析討論,Volvo冷態試驗條件下存在典型的鈍體尾流KH不穩定及BVK不穩定流動結構,其流動特征頻率分別為1405 Hz、135 Hz。其中,BVK不穩定流動由KH不穩定流動1/8諧波相應發展形成。以上流動模態在存在相應頻率擾動時可能會被激發為不穩定流動狀態,需在實際工程應用中進行合理規避。

