海雜波中基于可控虛警K近鄰的海面小目標檢測

郭子薰 水鵬朗 白曉惠 許述文 李東宸

①(西安電子科技大學雷達信號處理國家重點實驗室 西安 710071)②(中國船舶工業系統工程研究院 北京 100094)

1 引言

對于海面警戒雷達來說，在小擦地角下提高海面小目標的檢測能力是一項長期且困難的工作，這類小目標主要指浮冰、小船、蛙人和飛機殘骸等[1]。大致原因如下：第1，小目標具有很小的雷達截面積(Radar Cross Section, RCS)和較弱的雷達回波；第2，海雜波具有復雜且變化的特性，例如較寬的多普勒帶寬和較強的非高斯特性等[2]。為了檢測小目標，通常采取兩種方式：高分辨率和長觀測時間，其中前者可以降低雜波功率水平，后者可以增加目標回波的累積增益。但是在傳統雷達中，會面臨一個波位上長駐留時間和掃描效率上的矛盾。隨著雷達系統的不斷發展，2003年麻省理工(Massachusetts Institute of Technology, MIT)的林肯實驗室[3,4]提出了泛探雷達(ubiquitous radars)，其同時利用多個接收波束覆蓋整個觀測空域實現了在所有方向下的全時觀測。所以，在長觀測時間下提出一種有效的檢測小目標的方法是有必要的。但是，由于海雜波的長時非平穩特性和目標回波復雜的幅度和多普勒調制，海雜波和目標回波都很難被建模為簡單有效的參數模型[5]。隨著對海雜波和小目標回波的深入研究，研究者提出了時頻分析、分形特性和機器學習等方法[6—8]來解決這一類問題。總的來說，都是通過研究海雜波和目標回波在各個域上的不同特性來對二者進行區分。

在1993年，Haykin等人通過對海雜波時間序列的分形(fractal)特性進行研究，進一步發現分形維數可以被用作特征以幫助實現目標檢測。為了使用更多的特征來提高檢測性能，Shui等人[9]進一步提取了1個幅度特征和2個多普勒特征，并將3個特征聯合起來建立特征空間中的三維凸包以實現最終檢測。通過IPIX雷達數據集[10]的驗證，基于3特征的檢測器與基于單特征的檢測器相比，實現了更優的檢測性能。這可以歸功于多個來自不同域互補的有效特征的聯合使用。但是，目標回波有時會落入多普勒域的主雜波帶內，這大大影響了檢測結果。為了解決這一問題，另一種基于時頻3特征的檢測器被Shui等人[11]提出，大大改善了檢測器的性能。但是，通過對檢測結果的研究發現，兩個基于3特征的檢測器分別在不同的數據上表現優異。考慮到不同特征對不同數據的敏感性，聯合使用更多的互補特征來設計高維空間中的檢測器就成為了進一步提高檢測性能的有效途徑。

在機器學習領域中，有很多分類能力優異的算法，比如支撐矢量機(Support Vector Machine,SVM)、神經網絡(Neural Network, NN)等。我們嘗試將雷達目標檢測問題與機器學習算法結合起來，設計在高維特征空間中的檢測器。在本文中，為了獲得更好和更具有魯棒性的檢測結果，已有的來自不同域的7個有效特征被聯合使用，包括歸一化Hurst指數(Normalized Hurst Exponent,NHE)[12,13]、相對平均幅度(Relative Average Amplitude, RAA)、相對多普勒峰高(Relative Doppler Peak Height, RDPH)、相對向量熵(Relative Vector Entropy, RVE)[9]、脊累積(Ridge Integration,RI)、連通區域數目(Number of connected Regions,NR)和最大連通區域尺寸(Maximal Size of connected regions, MS)[11]。由于該多個特征使得雜波與目標都處于七維特征空間，從而一些已有的方法在高維(n＞3)空間中計算復雜度極高或者不再適用。例如，由于已有的基于3特征的檢測器[9,11]使用凸包來決定最終的判決區域，相繼通過收縮凸包實現虛警控制。但是，凸包只能在小于等于三維的空間中使用，一旦到四維或更高維，凸包的計算代價將會非常大，甚至無法計算，所以這就是其不能推廣到高維的原因。后來，本團隊為了突破維數限制的問題，提出了基于特征壓縮的檢測器[14,15]，可以將原本在高維空間中的特征壓縮至三維空間。與以往基于單特征或3特征的檢測器相比，基于特征壓縮的檢測器獲得了更加優異的性能。但是在特征壓縮的過程中，壓縮損失是不可避免的。本文不僅為了利用更多的已知特征使得對目標有更好的檢測，同時也為了避免壓縮來帶的性能損失，使用了機器學習中的K近鄰(K Nearest Neighbours, K-NN)算法。但是由于K-NN無法實現對虛警率的有效控制，所以本文提出了一種基于可控虛警的改進K-NN方法，有效地解決了問題。

本文的工作安排大致如下：第2部分先回顧所使用的特征，并介紹一種典型的仿真目標回波產生器；第3部分提出了基于可控虛警的改進K-NN檢測方法；第4部分利用實測數據對所提出的檢測器進行性能評估，并與其它基于特征的檢測器進行對比和分析；最后，第5部分會對本文的工作進行總結評價。

2 仿真目標回波產生器及7特征概述

雷達目標檢測問題可以歸結為以下2元假設檢驗問題[5,9,11,13—15]

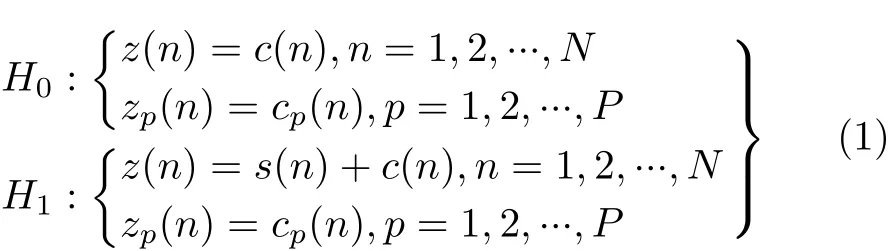
其中，z(n)和zp(n)分別表示待檢測單元和周圍參考單元所接收的復時間序列，c(n)和cp(n)分別表示待檢測單元和周圍參考單元的純雜波時間序列，s(n)表示目標回波時間序列，P為參考單元數目，N為脈沖長度。在零假設H0下，待檢測單元所接收的時間序列為純雜波，其具有與周圍參考單元的雜波序列相同的統計特性和多普勒特性。在備擇假設H1下，待檢測單元所接收的時間序列為帶有目標的回波時間序列。

2.1 7種有效特征概述

在檢測器的設計中，7種有效特征被使用，包括兩個幅度特征：NHE, RAA[9,12,13]，兩個多普勒特征：RDPH, RVE[9], 3個時頻特征：RI, NR,MS[11]。對于兩個幅度特征，若雷達回波數據包含目標，則其NHE和RAA的取值均大于純雜波。此外，我們對回波數據的多普勒幅度譜進行分析并提取有效特征RDPH和RVE，當發現待檢測單元包含目標時，RDPH較大，RVE較小；當待檢測單元為純雜波時，RDPH較小，RVE較大。但是，目標回波容易落在多普勒域的主雜波帶內，使得前4種特征不再適用，那么3個時頻特征就可以在這種情況發揮作用幫助完成目標檢測。當雷達回波包含目標時，RI和MS取值較大、NR取值較小；反之，當回波是純雜波時，RI和MS取值較小、NR取值較大。

通過提取7個有效的海雜波和目標的特征，目標檢測問題就可以近似地被轉化為一個在七維特征空間的二分類問題。由于不同的特征對不同的數據或者海態都有不同的敏感性，那么基于單個特征的檢測器就不會對任何情況都適用和有效。對目標檢測問題來說，聯合使用7個有效特征來構建高維特征空間中的檢測器無疑是一種綜合有效的方法。

2.2 仿真目標回波產生器

由于海面小目標的多樣性和目標與海表面之間復雜的相互運動，獲取所有種類的目標的有效信息是不可能的。考慮到雷達的工作模式，大量的雜波數據可以被快速地收集，相比之下，只有少量的目標數據被獲取，這就導致了兩類樣本數量的不均衡。在我們的工作中，使用已有的雜波信息對典型目標回波進行仿真以輔助完成后續檢測器的設計。具有勻速和勻加速運動狀態的典型小目標回波可以被表示為[15]

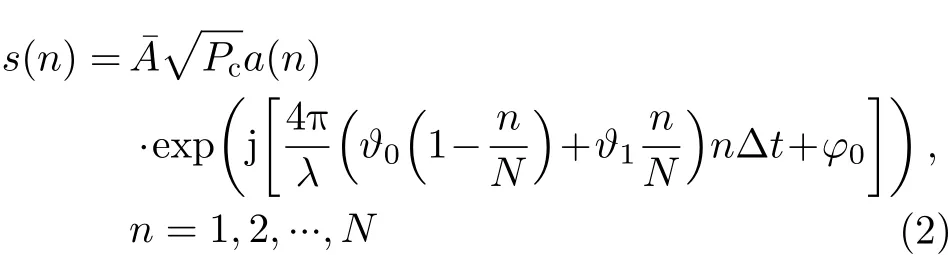
通過對公開IPIX數據集的研究發現，當信雜比低于—10 dB時，目標無法被檢測到；當信雜比高于20 dB時，目標一定可以被檢測到，所以將經驗參數 Aˉ設置為[—10 dB, 20 dB]的對應區間[10—1,101/2]上的均勻分布，用于調節信雜比，Pc是雜波的平均功率，a(n)是一個高度相關的取值為非負的隨機序列，被用于模擬小目標的幅度波動， λ是雷達的工作波長， ?0和 ?1分別是目標的初始和終止徑向速度， Δt是 雷達的脈沖重復周期， φ0是隨機分布于區間[0, 2π]上的初始相位，N是仿真目標回波信號的長度。

考慮到小目標幅度的物理特性，幅度序列a(n)被建模為一個非負的、高度相關的、單位功率的隨機序列，并具有可調動態范圍和去相關時間。序列a(n)的生成步驟分為如下4步：第1，生成一個獨立、同服從在區間[0, 1]上均勻分布的序列u(n)；第2，由于幅度序列具有高度的空時相關性，所以將隨機序列u(n)作為一個1階自回歸模型的輸入[15]

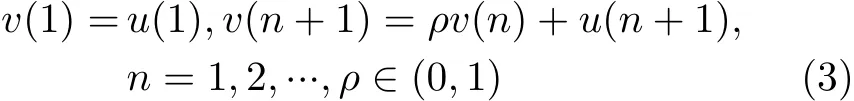
即可產生高度相關的序列v(n)，其中 ρ ∈[0.95,0.99]表示1階相關系數，經計算，此處序列v(n)的取值范圍在區間[—1/(1 -ρ ) , 1/(1 -ρ)]內；第3，由于目標的幅度為非負值，所以將序列v(n)轉化為一個非負的序列v+(n)

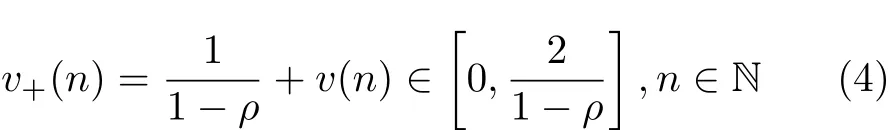
第4，由于剛開始產生的幅度序列不夠穩定，所以為了避免這種情況我們只選取后續產生的幅度序列v+(n+M)，其中M是一個足夠大的正數，再對序列進行功率歸一化，即可得到最終的幅度序列a(n)

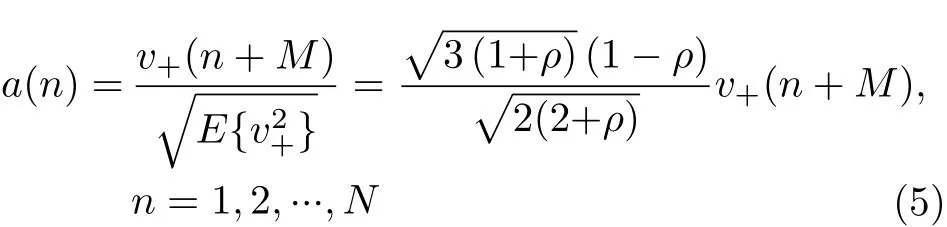
其中，E{v+2}是序列v+(n)的功率。

此外，初始徑向速度 ?0和 終止徑向速度 ?1可以被表示為[15]

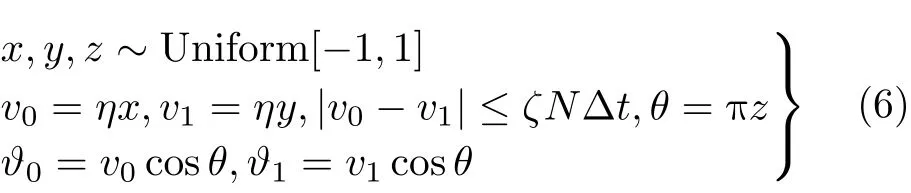
其中，θ為雷達視線與目標運動方向的夾角，服從[—π, π]上的均勻分布，v0和v1分別表示目標的初始速度和終止速度，隨機數x,y,z是相互獨立的。值得注意的是，當加速度的限制條件不滿足時，隨機數x和y需要重新產生。在目標回波仿真過程中，η的經驗取值為5 m/s, ζ的經驗取值為2 m/s2，其對應于小目標的速度在[—5 m/s, 5 m/s]之間，不超過10節，最大加速度為2 m/s2。通過上述步驟，一個典型的仿真目標回波產生器被構建。需要注意的是，該仿真目標回波產生器旨在生成足量的不完備的目標回波樣本，為后續檢測器的設計提供更多有效信息，而不是覆蓋各種各樣的目標回波。

圖1是在HV極化下第1組數據的真實目標回波和仿真目標回波的7個特征的對比圖，其中真實目標特征用藍色表示，仿真目標回波用紅色表示。由此可知仿真目標回波產生器的有效性，進一步仿真目標回波的特征與真實目標回波的特征也是十分接近的。

3 基于可控虛警的改進K-NN方法

很多機器學習算法可以有效地解決分類問題，比如SVM, K-NN, NN等。但是普通的二分類問題和目標檢測問題存在著兩點不同：第一，在普通的二分類問題中，兩類樣本的數量是均衡的，但是在目標檢測中，雜波數據遠遠多于目標數據；第二，普通的二分類問題中，兩類錯分概率是等價的，但是在目標檢測中，虛警概率比漏檢概率更重要(通常，虛警概率要低于10—3而漏檢概率可能達十分之幾)。這兩點不同導致機器學習中用于分類問題的算法不能直接使用在目標檢測問題中。其中，兩類樣本數量不均衡的問題已經被所提出的仿真目標回波產生器所解決，但是實現虛警可控仍是一個難題。

3.1 傳統K-NN算法概述

許多學者都在研究機器學習算法，用于分類和回歸問題。K-NN算法是一種簡單有效的非參數分類算法，其經常用于許多的模式識別問題。K-NN算法使用訓練數據本身直接對測試樣本進行分類[16,17]。首先尋找到與測試樣本最相似的k個訓練樣本(稱之為近鄰)，之后將k個近鄰中最主要的類別定為待測樣本的類別，其中樣本之間相似性度量以距離計算為準。為了獲得k個近鄰，測試樣本需與每個訓練樣本進行距離計算。

具體算法步驟可描述如下：

xtest ∈Rd

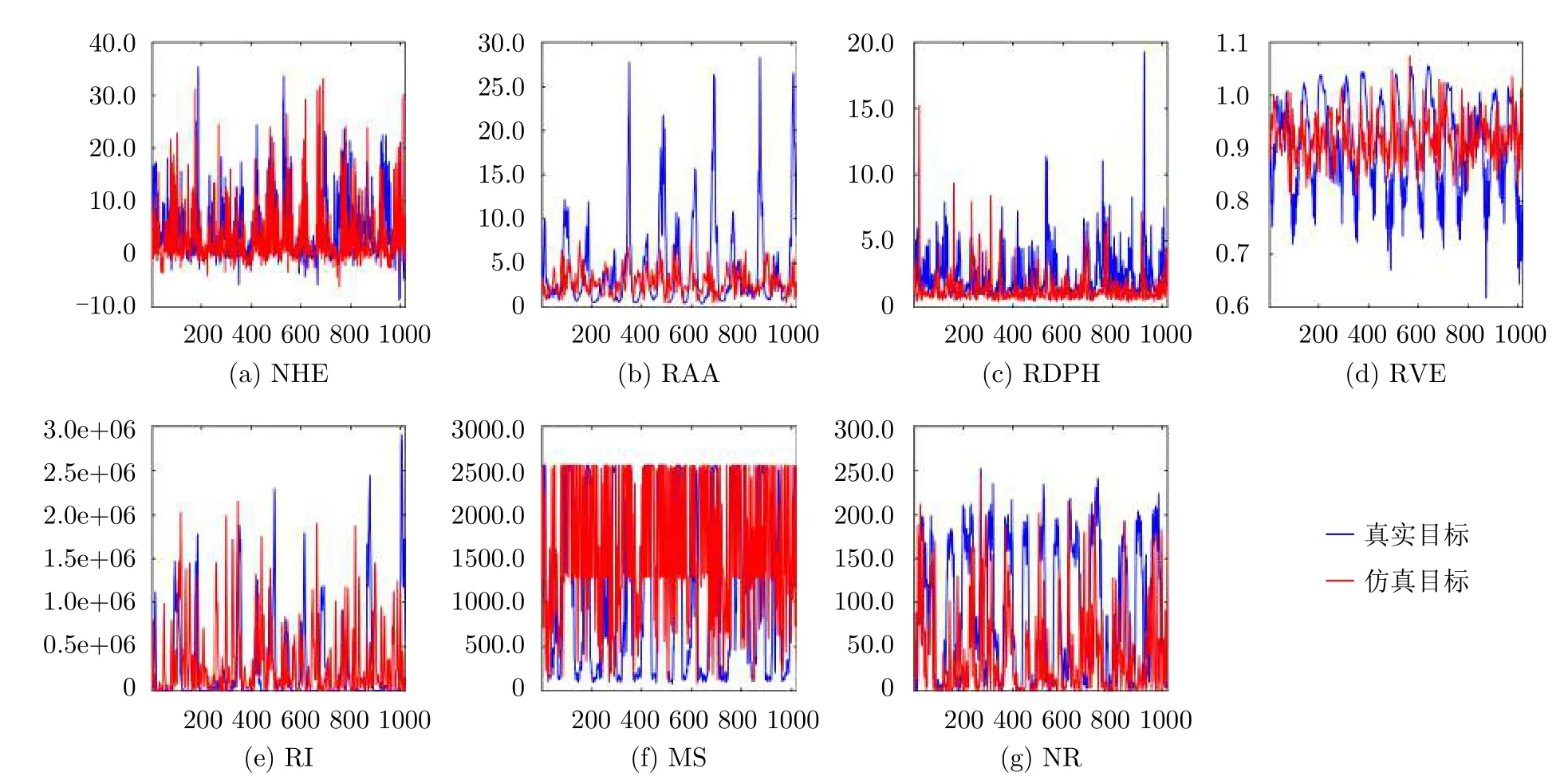
圖 1 仿真目標7特征與真實目標7特征對比圖Fig. 1 The comparisons of seven features of simulated targets returns and real targets returns

(1) 給出一個測試樣本 和訓練樣本集合Xset，其中，xi是訓練集合中第i個訓練樣本，計算測試樣本和每個訓練樣本之間的歐式距離

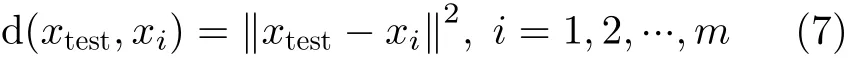
其中，m是訓練樣本的數目，d(x,y)表示計算x與y之間歐氏距離。

(2) 將所有距離{d(xtest,xi),i=1, 2, ··,m}從小到大進行排序，選取k個最小的距離值{d(xtest,xi1),d(xtest,xi2), ··, d(xtest,xik)}所對應的k個訓練樣本{xi1,xi2, ··,xik}，此處稱之為k個近鄰。

(3) 令 li為 訓練樣本 xi的類標(也可稱之為類別)，并認為k個近鄰中最主要的類標即為測試樣本的類標，即

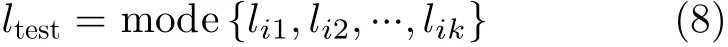
其中， ltest表 示測試樣本的類標，操作 m ode{·}表示計算集合中所有元素的眾數。

由于簡單的判決準則，即測試樣本的類標取決于k個近鄰中最主要的類標，K-NN算法被廣泛使用。但是，在目標檢測中，虛警概率和漏檢概率是不均等的，往往我們對虛警概率的控制要求更為嚴格。此外，機器學習算法通常要求兩類樣本的數目近似相等。所以，機器學習算法中可用于解決二分類問題的算法不可以直接使用在雷達目標檢測中。

3.2 基于可控虛警的改進K-NN海面小目標檢測

之前的很多關于K-NN算法的研究普遍集中于尋找最優的k值以提高檢測器的性能。如果要將KNN算法使用在雷達目標檢測問題中，準確地控制虛警概率則是重要而且必不可少的。雖然凸包學習算法[9,11]可以精準地控制虛警概率，但是它只能被用于單分類問題，以及只能在低維空間(n≤3)中使用。因此，凸包學習算法便不再適用于高維空間兩分類問題。一種改進的基于可控虛警的K-NN方法被提出，具體過程如下：

(1) 通過雷達接收機獲取海雜波時間序列c(n)；

(2) 仿真目標的產生：使用仿真目標回波產生器產生與海雜波數據等量的仿真目標回波數據s(n)；

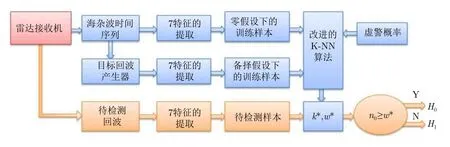
圖 2 所提檢測器的流程圖Fig. 2 The flowchart of the proposed detector

(3) 提取有效特征：對雜波序列c(n)和目標回波序列s(n)分別提取7個有效的特征，構成七維特征向量，并將其組成特征矩陣S0和S1，則訓練樣本集為S=S0∪S1，其中，S為m×n的矩陣，m=7是特征數量，n是海雜波和仿真目標樣本數目之和；

(4) 對于當前測試樣本集中的每一個測試樣本也提取同樣的7特征并構成特征向量，計算其與所有訓練樣本之間的歐式距離，得到距離向量D；

(5) 將距離向量D中的元素按照從小到大的順序進行排列，并取k個最小距離值所對應的k個訓練樣本，構成k近鄰；

(6) 計算k近鄰中，原本屬于海雜波樣本S0的數量n0和原本屬于目標樣本S1的數量n1，其中n0+n1=k；

(7) 設置一個閾值w，若n0≥w，則測試樣本被分類為海雜波，否則認為其是目標；

(8) 通過多次實驗，經驗地選取一個閾值w*，固定其保持不變，改變近鄰數目k的取值，使得實現的虛警概率Pfa和預設的虛警概率Pf之間差的絕對值小于一個極小值，將最終符合虛警要求的近鄰數記為k*；

(9) 對于每個測試樣本，在k*個近鄰中，若n0≥w*，測試樣本被分為海雜波，否則被分為目標。

圖2是所提檢測器的流程圖，主要分為兩個部分：用藍色表示的離線操作部分和用黃色表示的在線操作部分，紅色為共用部分。離線部分包括海雜波的獲取、仿真目標回波的產生、零假設和備擇假設下兩類特征向量的提取和根據虛警要求對應的改進K-NN算法中參數的計算；在線部分包括待檢測回波的獲取、待檢測的特征向量的構成以及判決部分。

4 實驗與分析

4.1 實驗數據

實驗所用數據為20組(4種極化)駐留模式下的實測IPIX[7]海雜波數據，其雷達工作在X波段，fr=1000 Hz，除了第18組和19組數據的距離分辨率為15 m和9 m以外，其余均為30 m。前10組數據采集于1993年加拿大東海岸，測試目標是一個用錨固定的漂浮的直徑為1 m的塑料小球，隨著海浪上下運動，每組數據的時間序列長度為217，距離單元數目為14；后10組數據采集于1998年在加拿大安大略湖，測試目標是一艘低速運動的小船，每組數據由28個連續距離單元構成，每個距離單元包含60000個脈沖序列。具體的數據信息，如風速(Wind Speed,WS)、有效浪高(Significant Wave Height, SWH)、雷達視線與風速夾角以及目標所在單元和周圍影響單元如表1所示。

4.2 檢測器性能與分析

在圖3中，分別畫出了在IPIX雷達數據集上，4種極化下、觀測時間為0.512 s的多種檢測器平均檢測概率對比圖。通過比較發現，所提檢測器在76組數據上呈現出最優的檢測結果，剩下4組也是接近于最優檢測結果。可以得出結論，所提檢測器具有良好的檢測性能和穩定性。在表2中，通過觀察各種基于特征的檢測器[9,11,12]的平均檢測概率可以得知，使用單一特征或少量特征的檢測器的性能遠差于聯合使用多個有效特征的檢測器的性能。在圖4中，分別畫出了在IPIX雷達數據集上，四種極化下、觀測時間為1.024 s的多種檢測器平均檢測概率對比圖。通過對比發現，當觀測時間從0.512 s提升至1.024 s時，所有檢測器的性能均有提升。其中，基于分形的檢測器的性能從0.329提升至0.435，它是所有檢測器中提升效果最明顯的。但是所提出的檢測器的性能只從0.851提升至0.892，這是由于天花板效應。因為在觀測時間為0.512 s時，所提出的檢測器的平均檢測概率已經接近于1，所以它只有很小的空間以供性能的提升。

更進一步，為了驗證所提方法在多種虛警概率下的更優性能，本文對比了所提檢測器和其余檢測器在虛警概率為0.01時的檢測結果。如表3所示，通過實驗表明，所提檢測器在更高虛警率下，表現仍舊優異。

除此之外，為了進一步的分析7個特征在檢測過程中的貢獻，本文設計了7個僅使用6個特征的基于KNN的檢測器，即每個檢測器分別去掉1個特征。通過這7個基于6特征的KNN檢測器與所提出檢測器的性能差值來評估這些特征的重要性。具體結果如表4。

其中，性能損失為在相同條件下，所提出的使用7個特征的檢測器的檢概率減去使用6個特征的檢測器的檢測概率。由表4的結果可知，當所有特征中去掉RDPH時，對檢測性能的影響最大(其中HH極化下性能損失高達5.14%)，其他依次是RI,MS, RAA, NHE, RVE和NR。缺失某個特征后，在4種極化下的性能損失均有不同，不存在某個特征在4種極化下的貢獻都最低的情況。當然，也不存在某個特征在每組數據下都表現最優的情況，即各個特征在不同情況下或多或少都對檢測結果做出了貢獻，所以聯合使用多個來自不同域的特征也是很有必要的。總的來說，該檢測方法為一個開放的理論框架，允許更多有效且互補的特征加入以提高檢測器的性能。

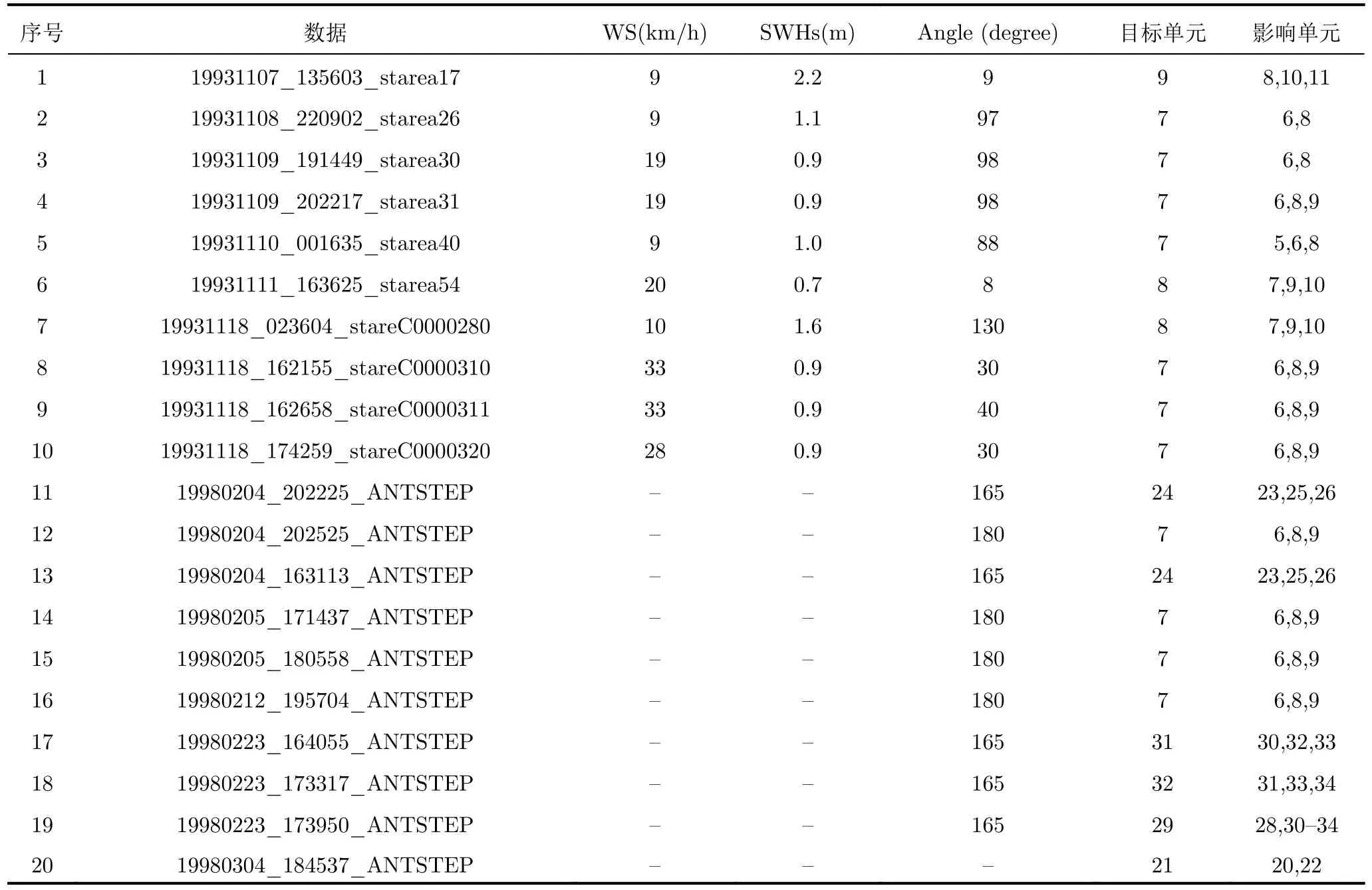
表 1 IPIX數據集描述[10]Tab. 1 Description of IPIX radar database[10]

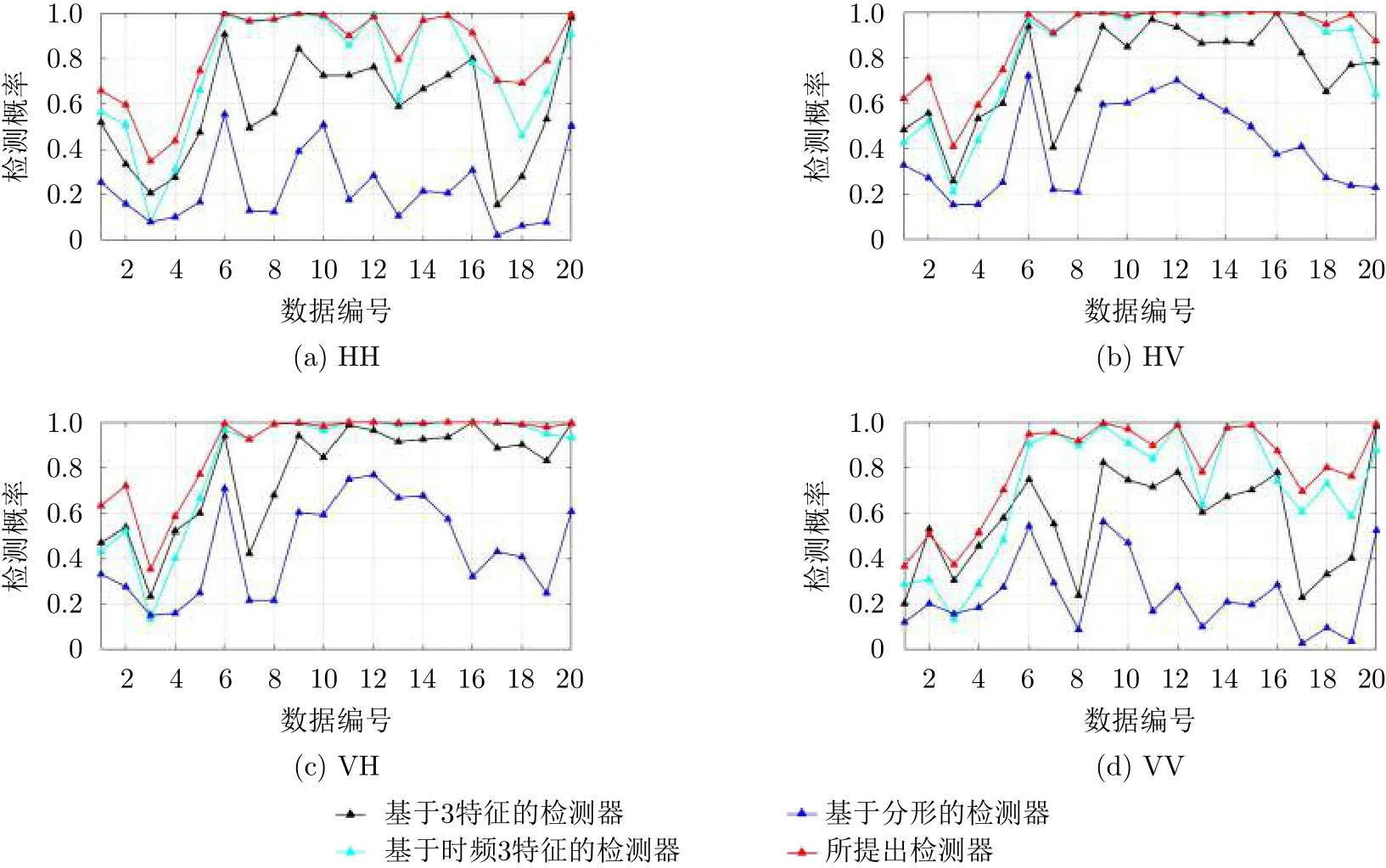
圖 3 所提檢測器與其余檢測器的檢測概率Fig. 3 Detection probabilities of the proposed detector and other detectors

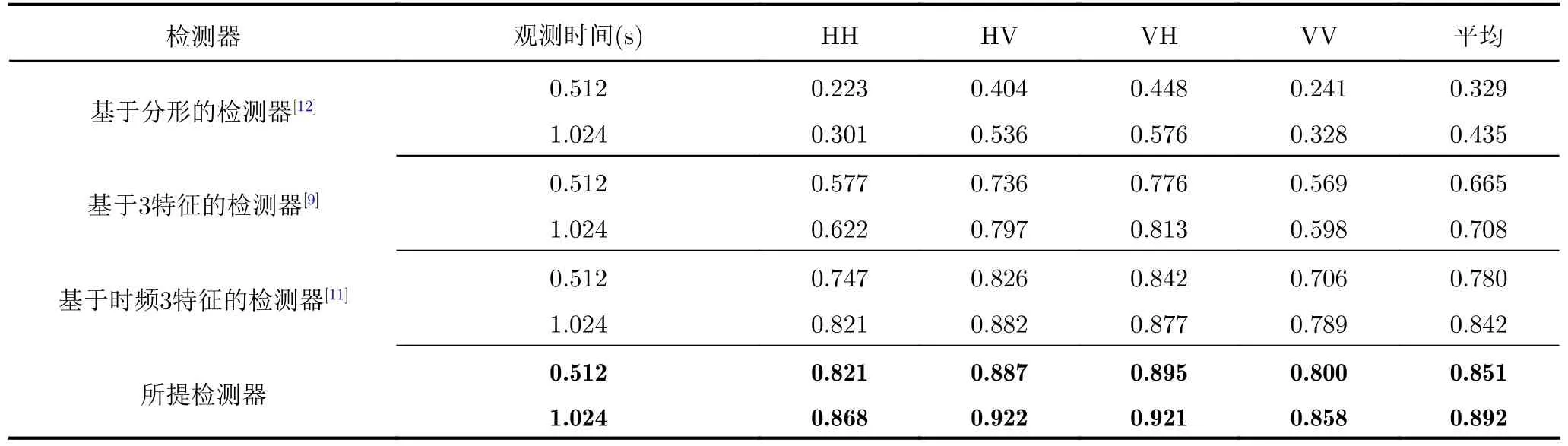
表 2 IPIX數據集上多種檢測器的平均檢測概率Tab. 2 The average detection probabilities of detectors on IPIX radar database

下面，為了印證本文所提方法對于虛警率的控制情況，圖5展示了k值的變化對虛警概率的影響。通過改變k的取值，就可以達到不同的虛警概率。本文中，當預設虛警率為0.01時，實際的虛警與預設的虛警之差的絕對值小于0.001即滿足要求；當預設虛警為0.001時，實際的虛警與預設的虛警之差的絕對值小于0.0001即滿足要求。最終所提出的檢測器在20組IPIX雷達數據集上實現的虛警如表5所示，其中4種極化的平均實現虛警率和所有極化的平均實現虛警率已列出，與預設虛警率相差甚微。由此可見，所提檢測器很好地控制了虛警率。

5 結論

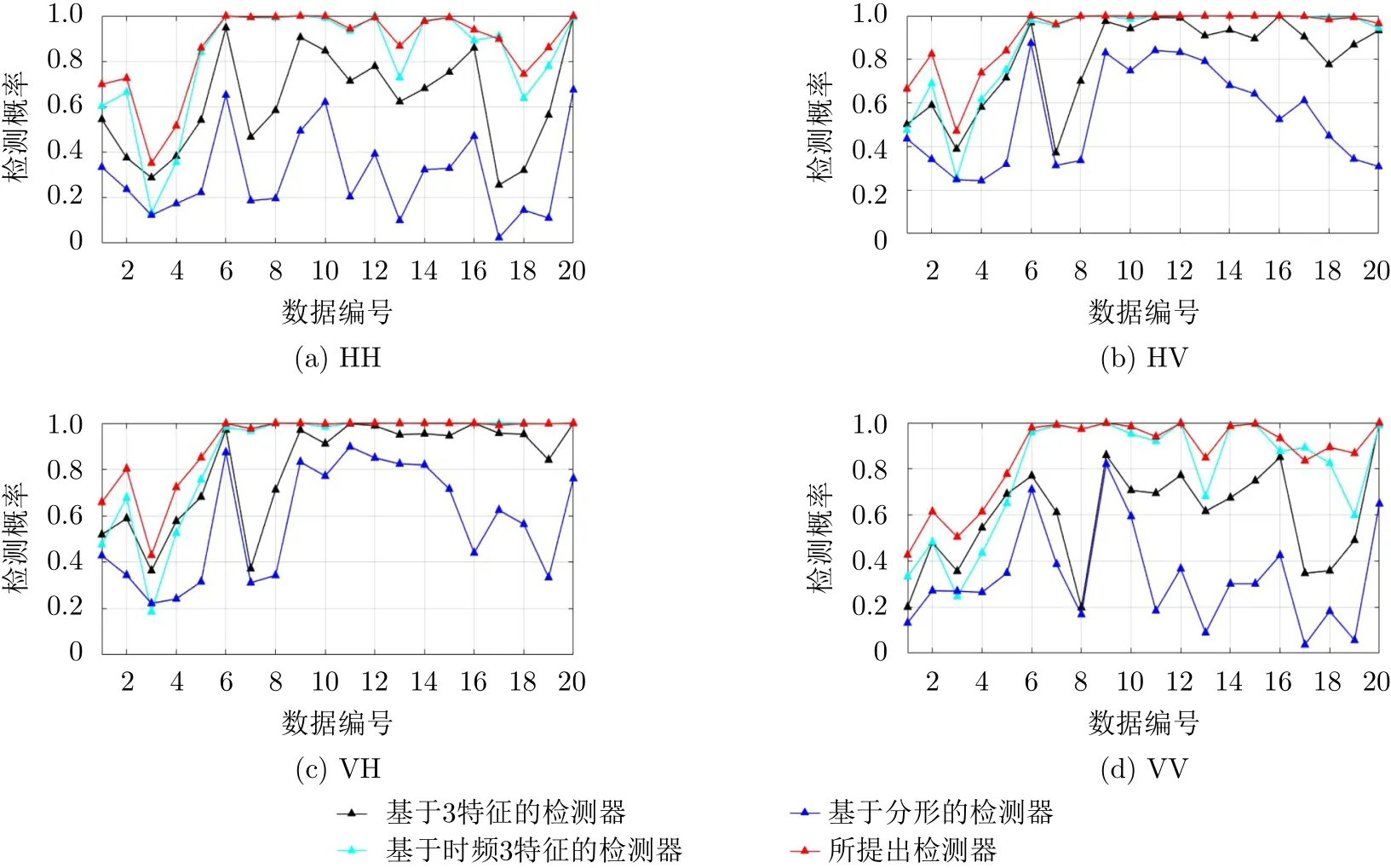
圖 4 所提檢測器與其余檢測器的檢測概率Fig. 4 Detection probabilities of the proposed detector and other detectors

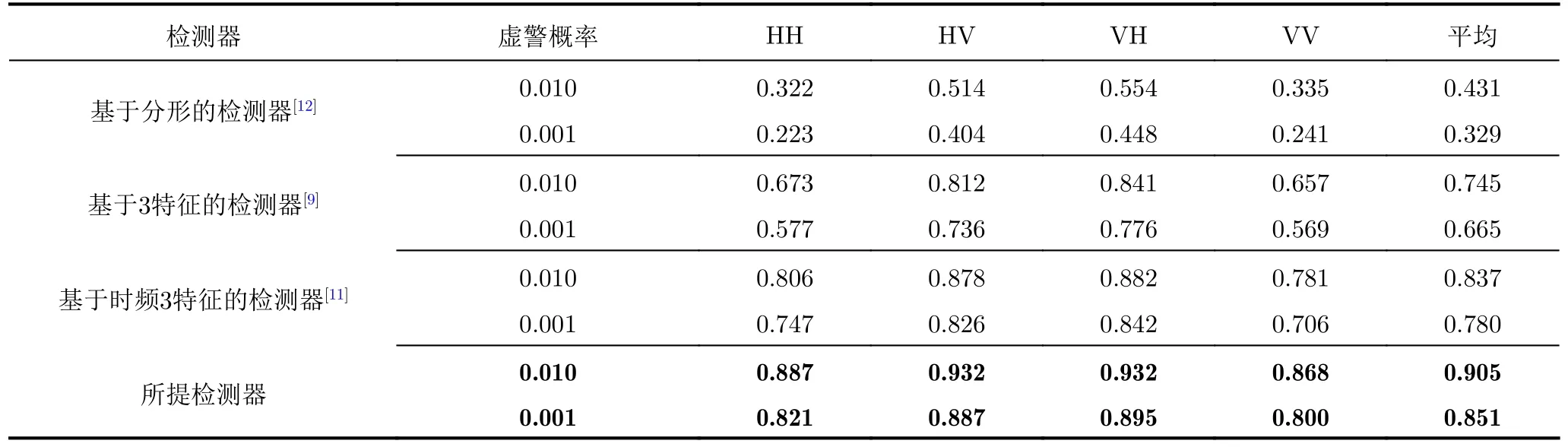
表 3 IPIX數據庫中20組數據的平均檢測結果對比Tab. 3 The comparisons of average detection results of 20 datasets on IPIX radar database

表 4 基于6特征的KNN檢測器在IPIX數據庫上20組數據的平均檢測結果對比 (%)Tab. 4 The average detection results comparisons of KNN-based detectors using six features at 20 datasets on IPIX radar database (%)

本文提出了一種高維空間中基于可控虛警K-NN的海面小目標檢測方法。現有的基于特征的檢測方法存在維數限制問題，維數限制問題嚴重地阻止了更多有效特征在目標檢測過程中的使用，更進一步限制了性能的提升。所提檢測器很好地解決了上述問題。考慮到普通的二分類算法中兩類樣本數目均衡的需求，使用一種典型的仿真目標回波產生器可產生與雜波等量的典型的仿真目標回波，為后續檢測器的設計起到輔佐的作用，使得目標信息被使用到訓練檢測器的過程。此外，通過改進機器學習中K-NN算法，實現了目標檢測問題中最重要的虛警率可控，即有效地將K-NN算法應用到了目標檢測中。最后通過公認的IPIX雷達數據集的驗證，本文所提檢測器與其余基于單特征或者3特征的檢測器相比，具有良好的檢測結果和魯棒性。

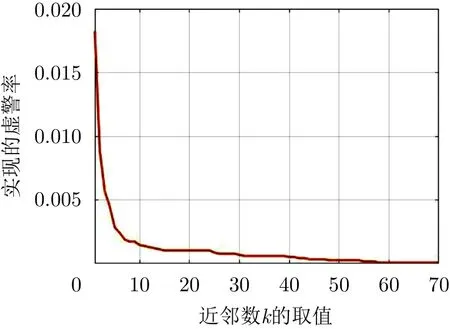
圖 5 k值不同時，所實現的虛警率變化圖，其中w*=3Fig. 5 Realized false alarm rate when k takes different values, where the w*=3

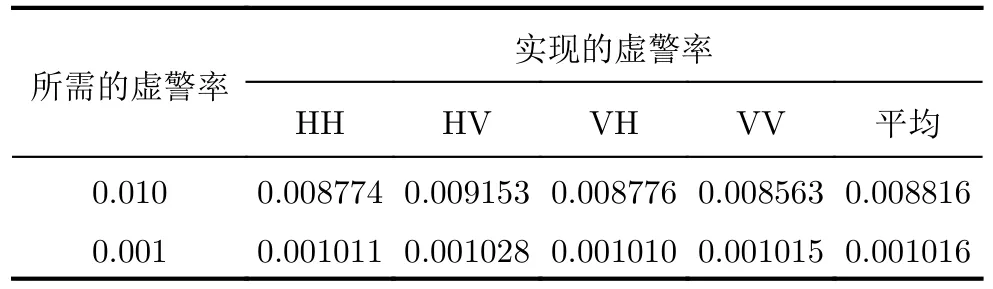
表 5 所提檢測器在20組IPIX雷達數據集上實現的虛警概率Tab. 5 The realized false alarm rate of the proposed detector of 20 datasets on the IPIX radar database