結合幅度信息的擴展目標隨機有限集跟蹤方法

柳 超 孫進平 陳小龍 張志國

①(北京航空航天大學電子信息工程學院 北京 100191)②(海軍92853部隊 葫蘆島 125106)③(海軍航空大學 煙臺 264001)

1 引言

多目標跟蹤的目的是從一系列被噪聲、漏檢和虛警污染的傳感器量測中估計出目標的數目和狀態[1]。解決此類問題的一個重要環節是建立量測和目標狀態之間的關系模型。傳統跟蹤方法[2]假設一個目標最多只能產生一個量測，所建立的模型稱為標準量測模型，目標被稱為點目標。這一模型顯著降低了多目標跟蹤的復雜度，因而獲得了廣泛應用。但是隨著傳感器技術的發展，標準量測模型在許多情況下已不再適用。一方面當傳感器的分辨率比較高或目標與傳感器之間的距離比較近時，目標可能會占據多個分辨單元，從而產生多個量測。例如，當采用車載雷達對車輛進行跟蹤和采用激光測距傳感器對行人進行跟蹤時，都可能引起一個目標產生多個量測的現象，且量測的分布往往能反映出目標的形狀特征。這種類型的目標稱為擴展目標[3]。另一方面，海上的艦船或空中的飛機等一些軍事目標經常以編隊的形式出現，當這些目標與傳感器之間的距離較遠時可能會出現一個“群”目標產生多個量測的情形。由于雷達分辨率的制約，群內的目標往往是不可分辨的，此時合理的處理方式是將這一群目標視為一個獨立的目標進行跟蹤，因而這類目標被稱為“群目標”。由于不滿足標準量測模型的要求，擴展/群目標的跟蹤需要采用非標準量測模型。

隨著信號處理以及計算機技術的發展，在過去的十多年間，對擴展/群目標跟蹤問題的研究已獲得越來越多的關注。由于群目標和擴展目標在量測過程上的相似性，許多文獻把它們作為一類目標進行研究。Gilholm和Salmond[3]假設每個時刻接收的量測數為泊松分布，在此前提下提出一種擴展目標跟蹤方法。Boers等人[4]采用類似的方法對具有一維擴展特性的“竿”形目標進行聯合檢測和跟蹤。Mahler[5]在文獻[3]所提模型的基礎上推導了一種擴展目標概率假設密度(Extended Target Probability Hypothesis Density, ET-PHD)濾波器，并指出ET-PHD實現的前提是對量測集進行合理劃分。Granstr?m等人[6,7]利用高斯混合(Gaussian Mixture,GM)實現了Mahler提出的ET-PHD濾波器，稱為ET-GM-PHD，并且提出了距離劃分和子劃分兩種量測劃分方法。但是在文獻[6,7]中，為降低算法的復雜度，作者只估計了目標中心的運動特性，而忽略了對目標擴展的估計。其后，為實現擴展目標數目的更準確估計，Orguner[8,9]用高斯混合實現了帶勢估計的PHD濾波器。Koch[10]在假設擴展目標具有橢圓形狀的前提下，提出了一種隨機矩陣模型[11–14]，對目標的運動狀態采用高斯分布建模，擴展狀態采用逆威沙特分布建模。Granstr?m[11]提出了基于該模型的高斯逆威沙特PHD(Gaussian Inverse Wishart PHD, GIW-PHD)濾波器，彌補了ETGM-PHD無法估計目標擴展狀態的不足，并且針對大小不同且空間鄰近的擴展目標分別提出了預測劃分和最大期望劃分方法。此外，一些學者還提出了其他量測劃分方法[15–17]。

目前，有關擴展目標跟蹤的文獻均直接或間接采用空間信息劃分量測，在雜波密集情況下一些雜波量測可能在某些劃分中被劃入目標單元，從而降低目標擴展狀態和運動狀態估計的準確度。為解決這一問題，將目標和雜波的幅度信息(Amplitude Information, AI)引入GIW-PHD濾波器，通過為量測單元疊加幅度似然，增大目標量測單元的權重，降低包含雜波的量測單元的權重，從而達到抑制雜波的目的。此外，為了降低雜波對計算中心量測的干擾，采用幅度加權的方法計算量測單元的質量中心，以取代文獻[11]中的幾何中心，從而可以獲得更準確的中心量測估計，并進一步提升對擴展目標的狀態估計準確度。

2 GIW-PHD濾波器

2.1 基本模型

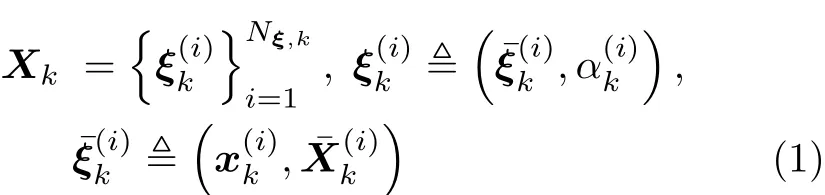
假設每個擴展目標的運動狀態服從線性高斯模型

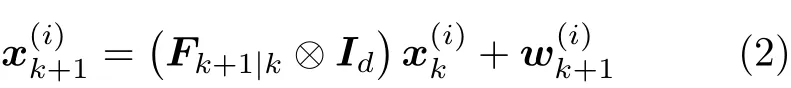
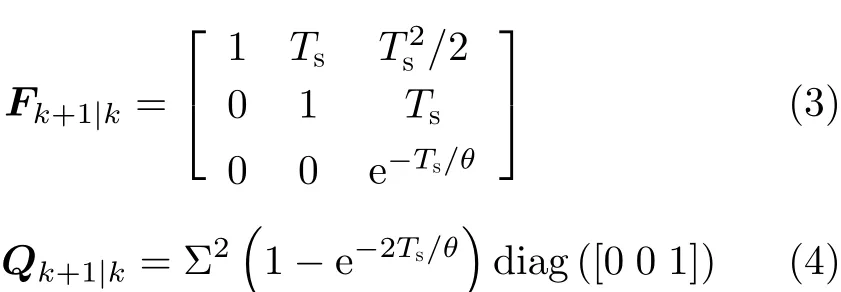
其中， Ts為 采樣間隔， Σ為 標量加速度標準差， θ為機動相關時間。

k時刻目標產生的量測集表示為

雜波量測數也采用泊松分布建模，單個時間單位體積內的泊松率為 βFA,k， 觀測區域的體積為 V，因此單位時間內雜波量測的均值為 βFA,kV。

2.2 GIW-PHD的具體實現

GIW-PHD濾波器[11]采用高斯逆威沙特分布的混合來近似 k時刻擴展目標的PHD

運動狀態的協方差和擴展狀態的估計為

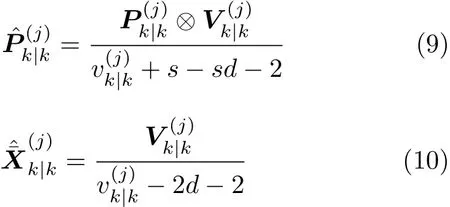
其中， s為目標運動狀態的維度。

GIW-PHD濾波器的具體濾波過程見文獻[11]，為節省篇幅，這里僅給出更新部分。

k時刻更新后的PHD為GIW的混合式

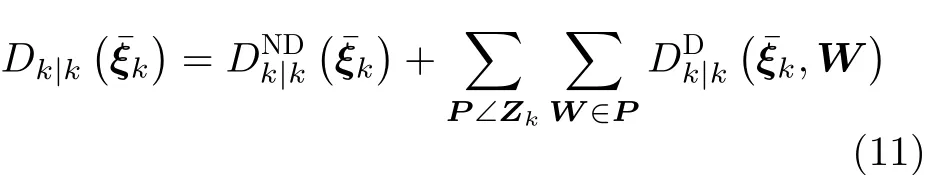
式(14)中的似然函數為

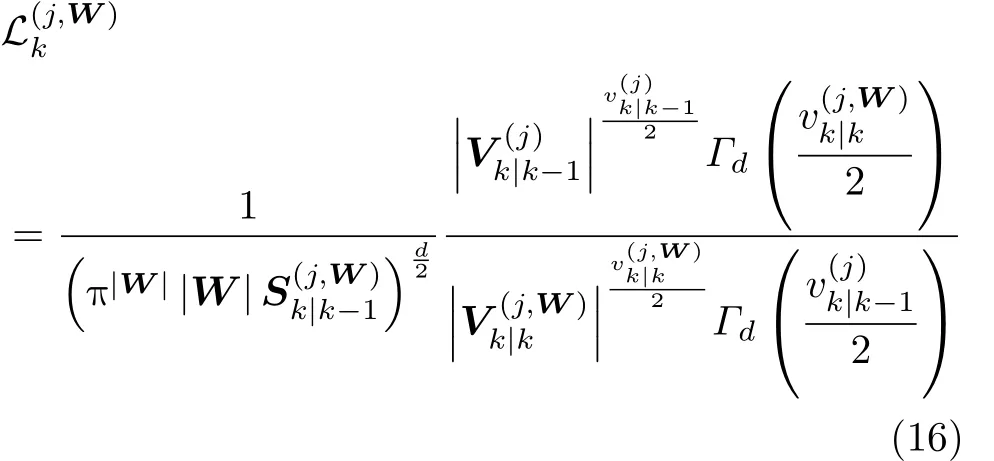
其中， |V|表 示 V 的 行列式，| W |表 示 W中的量測數。更新后GIW項的權重為

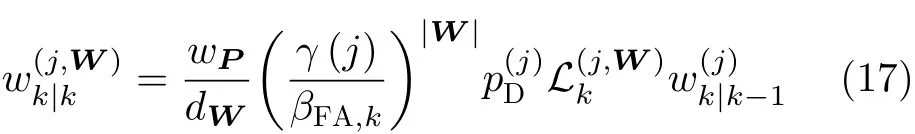
其中， wP為 某個劃分 P 的 權重， dW為某個量測單元 W 的權重[11]。式(13)～式(17)中下標為 k |k-1的量表示從 k -1時 刻到k 時刻的預測值。

3 基于幅度信息的GIW-PHD濾波器

圖1為擴展目標與量測的關系圖。其中，T1和T2為兩個大小不同的擴展目標，紅色圓點為擴展目標的量測，C1～C3為雜波。由圖中可見雜波C1距離目標量測較遠，容易劃入雜波單元；但是C2和C3距離目標量測較近，因而有可能在某種劃分下被劃入目標單元，導致目標擴展狀態的估計誤差，并影響運動狀態的估計效果。這種情況下，僅利用空間信息已經很難區分目標和雜波的量測，一種可能的途徑是利用目標和雜波的幅度信息。

圖 1 擴展目標量測Fig. 1 Measurements of the extended targets

Lerro[18]建立了幅度信息模型。Clark[19]將這一模型引入了標準PHD濾波器，并且用仿真證明利用目標的幅度信息可以更好的區分目標和雜波。但他所采用的標準PHD濾波器本身僅適用于標準量測模型即點目標，并不適用于擴展目標跟蹤場景[6]。本節給出結合幅度信息的GIW-PHD濾波器，稱為AI-GIW-PHD濾波器。通過將目標和雜波的幅度信息引入GIW-PHD濾波器，可以增大只包含目標量測的單元的幅度似然，而降低包含雜波量測的單元的幅度似然。由于GIW-PHD在濾波時需要考慮所有可能的量測劃分方法和量測子集，因此，這種操作的結果是估計目標擴展狀態和運動狀態時，僅包含目標量測的單元獲得的權重增大，而包含雜波量測的單元的權重降低，從而抑制了雜波對狀態估計的影響。

3.1 幅度信息建模

假定目標的幅度和運動狀態相互獨立，則 k時刻目標的量測似然函數 g (z|ξ)和雜波的量測似然函數 c (z)[19]可分別表示為

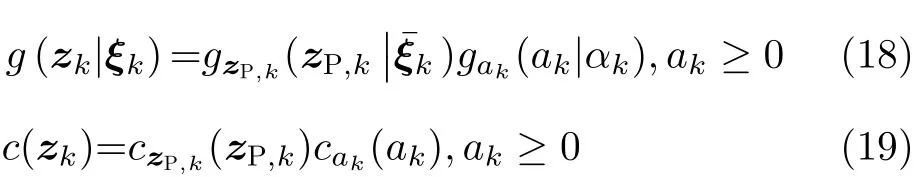
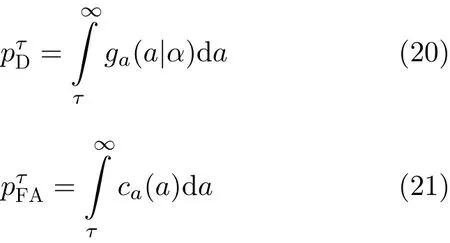
其中， τ為檢測門限。則過門限檢測后，目標和雜波的幅度似然函數分別為

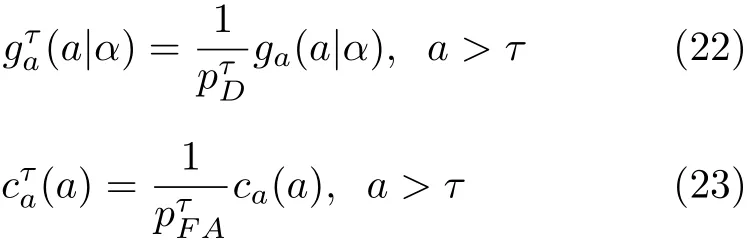
3.2 Rayleigh雜波下目標的幅度似然函數

當雜波為復高斯分布且幅度為Swerling 1型起伏時，雜波和目標的幅度為Rayleigh分布。雜波幅度的概率密度函數(Probability Density Function,PDF)為[19]

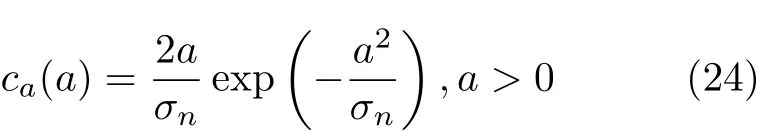
其中， σn為復高斯分布的協方差。目標幅度 Ak的PDF為

其中， σt為目標幅度的均方值。則目標加雜波的幅度的PDF為

由于信雜比的定義[19]為

將 σn和 α代入式(29)可得

3.3 AI-GIW-PHD濾波器

下面給出AI-GIW-PHD的具體算法。

由于AI-GIW-PHD只改進了GIW-PHD的更新部分，而預測部分保持不變，因此這里只給出AIGIW-PHD的更新步驟。

每個單元中所有量測的似然函數為

3.4 中心量測的計算

根據式(15(e))，當計算某個單元的中心量測時，對該單元中的所有量測取幾何平均值。然而，當該單元中混入了雜波量測時，采用這一方法將導致計算得到的中心量測偏離真實的中心量測，從而增大狀態估計誤差。為解決這一問題，計算中心量測時，采用幅度加權的方法來計算量測的質量中心，以取代式(15(e))中所用的幾何中心

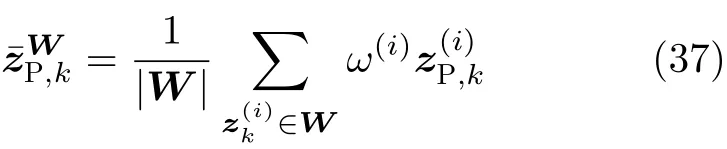
其中，幅度的加權因子 ω(i)為

其中， a(i)為 量測i的幅度。

通過幅度加權，當量測單元中包含了雜波時，由于通常情況下雜波的幅度小于目標量測的幅度，因此能夠更多地利用目標量測的信息，并減少雜波對中心量測的影響。

4 仿真

為檢驗所提AI-GIW-PHD算法的性能，通過仿真實驗將其與標準的GIW-PHD濾波器進行對比。

4.1 仿真設置

雷達觀測區域的面積為[–500, 500] × [–500,500] m。在總計31 s的觀測時間內有4個目標進入觀測區域。目標的真實航跡如圖2所示。圖中每種顏色的航跡代表一個目標，可以看到有2個擴展目標為勻速直線運動，另外2個目標為勻速轉彎運動，且目標的航跡之間出現了多次交叉。

目標的真實擴展為

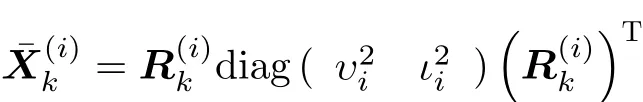
其中， R(i)為旋轉矩陣，用于保證目標的主軸平行

k于目標的運動方向， υi和 ιi分別為長軸和短軸的長度。本文仿真主要考察幅度對跟蹤性能的影響，因此4個目標的長短軸均為 (υi,ιi)=(20,5)。擴展目

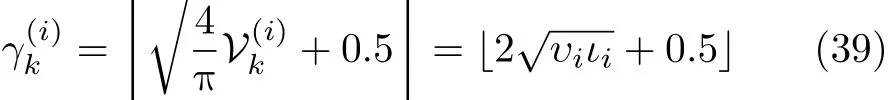
每個擴展目標產生的量測，在幅度上均獨立的服從參數為 σt的Rayleigh分布，且在幀間獨立的服從Swerling 1型起伏。

雜波在每一幀的總數服從均值為1000的泊松分布，虛警率為0.05，則理論上每一幀的虛警數服從均值為50的泊松分布。

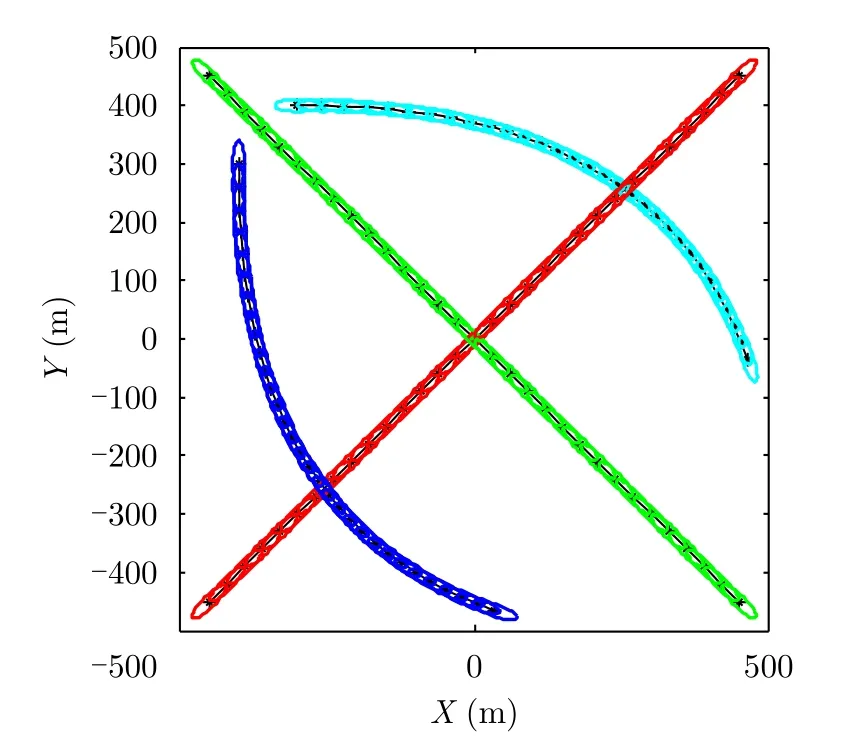
圖 2 擴展目標真實航跡(SCR=13 dB)Fig. 2 Real trajectories of the extended targets (SCR=13 dB)

設置目標的信雜比分別為SCR=13 dB和SCR= 6 dB。本文通過計算每種算法的OSPA誤差[20]來評價算法的跟蹤性能。

4.2 仿真結果

圖3，圖4為SCR=13 dB時未利用幅度信息的GIW-PHD和利用幅度信息的AI-GIW-PHD在某次仿真中的航跡濾波結果。圖3中，黑色“*”表示目標真實位置，紅色“O”表示狀態估計值。從該圖可以看到，GIW-PHD出現了比較明顯的航跡漏檢現象。這是因為當雜波率較高時，目標量測與雜波量測有可能相距很近，狀態估計容易受到雜波的干擾，導致一些GIW項權重降低，從而估計出的目標數目也會減少。圖4中，藍色“.”表示目標真實位置，黑色“O”表示狀態估計值。可以看到，利用了幅度信息的AI-GIW-PHD可以非常準確地估計出目標航跡，基本上沒有漏檢。這是因為，由于采用了幅度信息，相距較近的目標和雜波的量測能夠得到更好的區分，從而降低了雜波對目標GIW項的干擾。

圖5為GIW-PHD在該次仿真中的擴展狀態估計結果。圖5中綠色填充帶表示目標的真實擴展狀態，紅色橢圓表示GIW-PHD估計出的目標擴展狀態。可以看到，由于存在大量的航跡漏檢，GIW-PHD對目標擴展狀態的估計也出現了大量漏檢。當能夠估計出目標航跡時，GIW-PHD也能夠比較準確地估計出目標的擴展狀態，但在濾波開始時刻還存在比較明顯的估計錯誤。

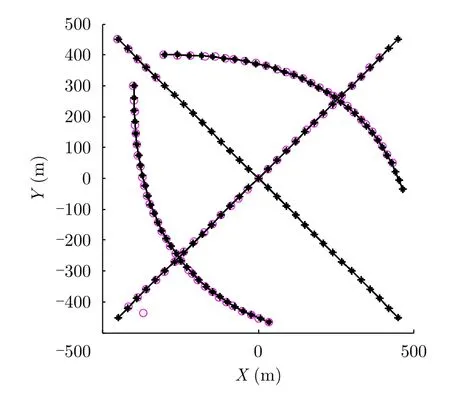
圖 3 GIW-PHD單次航跡估計結果(SCR=13 dB)Fig. 3 Track estimation of the GIW-PHD in a run (SCR=13 dB)

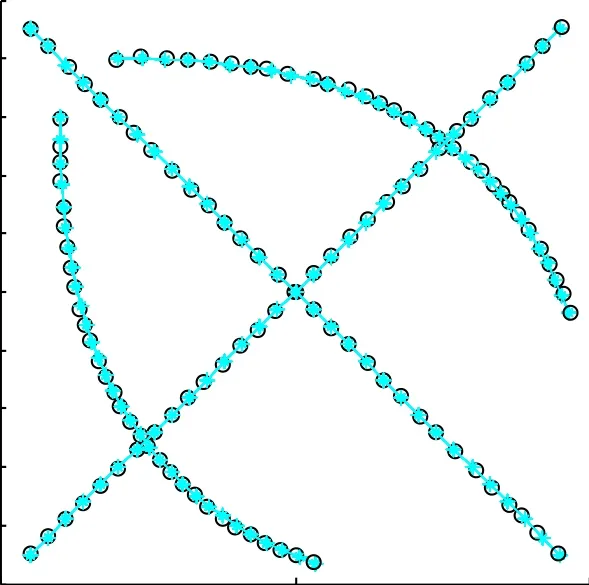
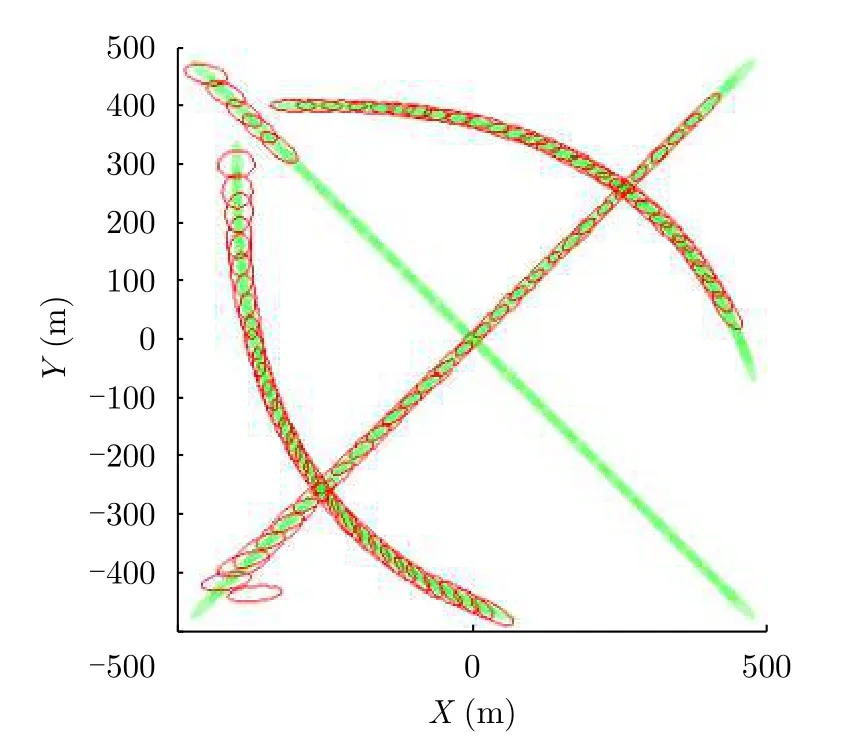
圖 5 GIW-PHD單次擴展狀態估計結果(SCR=13 dB)Fig. 5 Extended state estimation of the GIW-PHD in a run (SCR=13 dB)

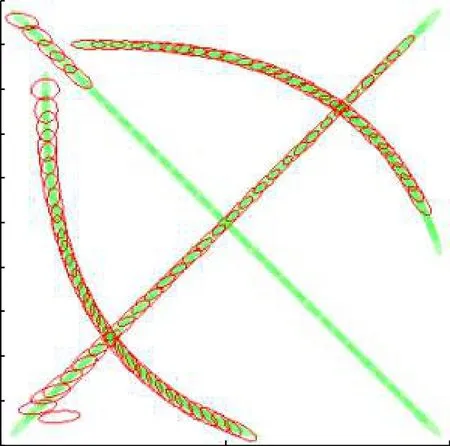
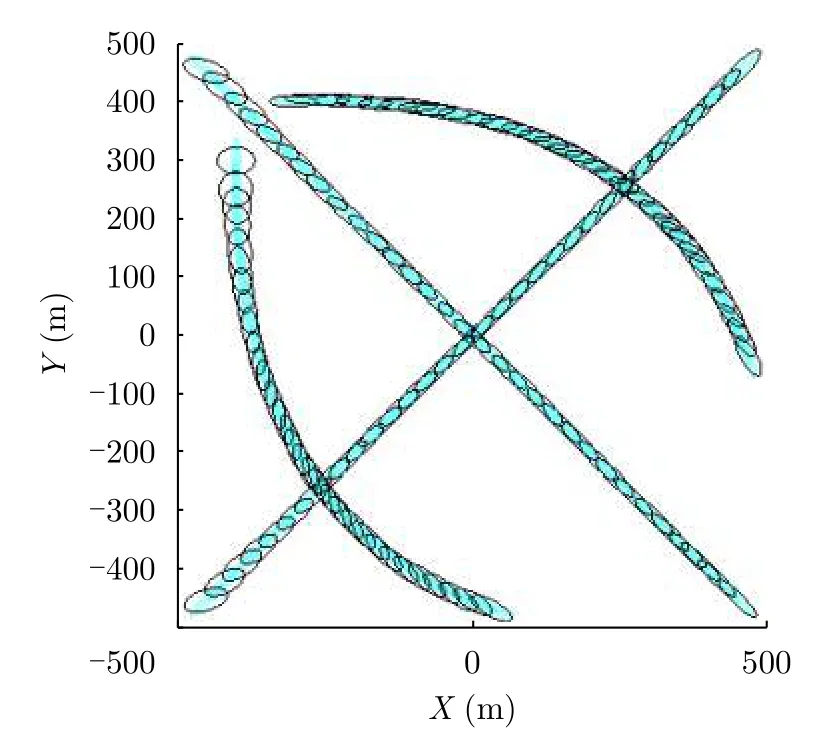
圖 6 AI-GIW-PHD單次擴展狀態估計結果(SCR=13 dB)Fig. 6 Extended state estimation of the AI-GIW-PHD in a run (SCR=13 dB)

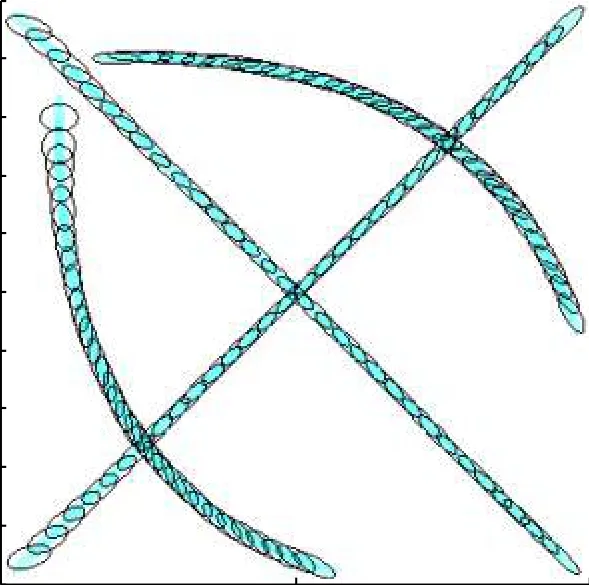
圖6為AI-GIW-PHD在該次仿真中的擴展狀態估計結果。圖6中藍色填充帶表示目標的真實擴展狀態，黑色橢圓表示AI-GIW-PHD估計出的目標擴展狀態。可以看到，AI-GIW-PHD始終能夠比較準確地估計出目標的擴展狀態，并且在濾波初始時刻也沒有出現明顯的錯誤估計。

圖7為SCR=13 dB時GIW-PHD和AI-GIW-PHD經過20次蒙特卡洛仿真后統計得到的平均OSPA位置誤差。可以看到，在大部分時刻AI-GIW-PHD的誤差比GIW-PHD稍大一些。但是，這并不能說明AI-GIW-PHD的濾波性能不如GIW-PHD。這是因為與單目標跟蹤時位置誤差的計算不同，多目標跟蹤時OSPA位置誤差的計算需要統計所有航跡的濾波誤差。由于GIW-PHD出現了明顯的航跡漏檢，用于誤差統計的航跡數少于AI-GIW-PHD，因而統計得到的OSPA位置誤差小于AI-GIW-PHD。當GIW-PHD不發生漏檢時，其位置誤差會更大。這與文獻[19]中的情況相似。雖然從圖7無法直接判定GIW-PHD和AI-GIW-PHD的濾波性能，但是根據圖3、圖4可以看到，當沒有漏檢時，這兩種算法都能夠準確地跟蹤目標。

圖8為SCR=13 dB時GIW-PHD和AI-GIW-PHD經過20次仿真后得到的平均目標數目估計值。可以看到，隨著濾波的進行，GIW-PHD總體上會出現越來越明顯的數目欠估計現象。這是因為雜波對GIW項的干擾越來越嚴重。相比之下，結合了幅度信息的AI-GIW-PHD始終保持了對目標數目的準確估計。這是因為，通過利用幅度信息，雜波與目標量測的區分會更加容易，從而使GIW項受到的雜波干擾顯著下降。

圖9為SCR=13 dB時GIW-PHD和AI-GIW-PHD經過20次仿真后得到的平均OSPA勢誤差。通過該圖，可以更加清楚地看到在目標數目估計方面，AI-GIW-PHD顯著優于GIW-PHD。這再次證明了幅度信息對擴展目標跟蹤的有效性。

圖10為SCR=6 dB時GIW-PHD和AI-GIW-PHD經過20次仿真后統計得到的平均OSPA位置誤差。結合圖10和圖7可以看到，隨著SCR從13 dB降到6 dB，未采用幅度信息的GIW-PHD的跟蹤誤差明顯增大，而采用了幅度信息的AI-GIW-PHD的跟蹤誤差變化不大。這是因為當SCR降低后目標的檢測概率也會下降，因而GIW-PHD算法中GIW項受到的雜波干擾會大大增加，導致狀態估計出現較大偏差。相比之下，AI-GIW-PHD由于利用了幅度信息從而能夠較好地區分目標和雜波，減輕了GIW項受到的雜波干擾，保持了狀態估計的準確度。

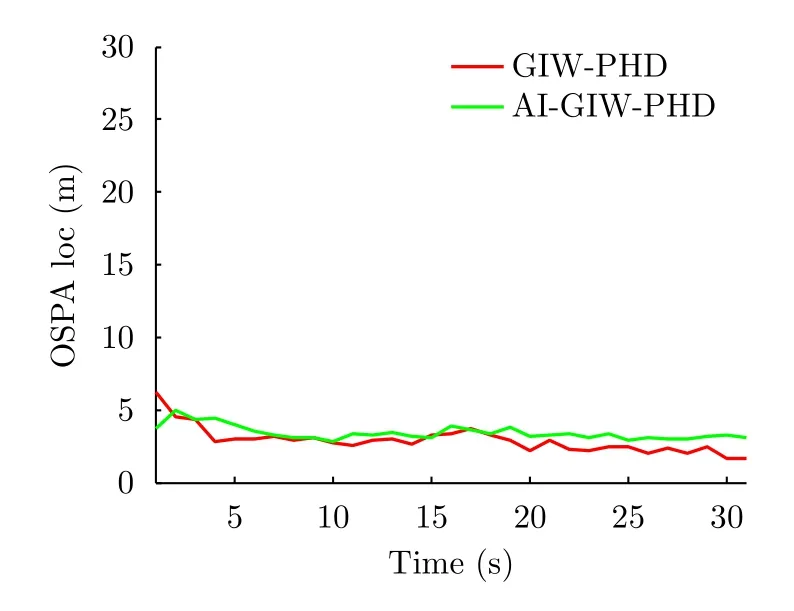
圖 7 平均OSPA位置誤差(SCR=13 dB)Fig. 7 Averaged OSPA location error (SCR=13 dB)

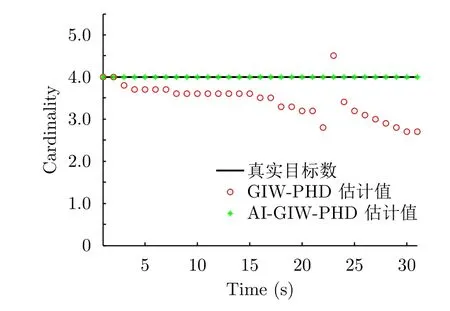
圖 8 平均勢估計結果(SCR=13 dB)Fig. 8 Averaged cardinality estimation (SCR=13 dB)

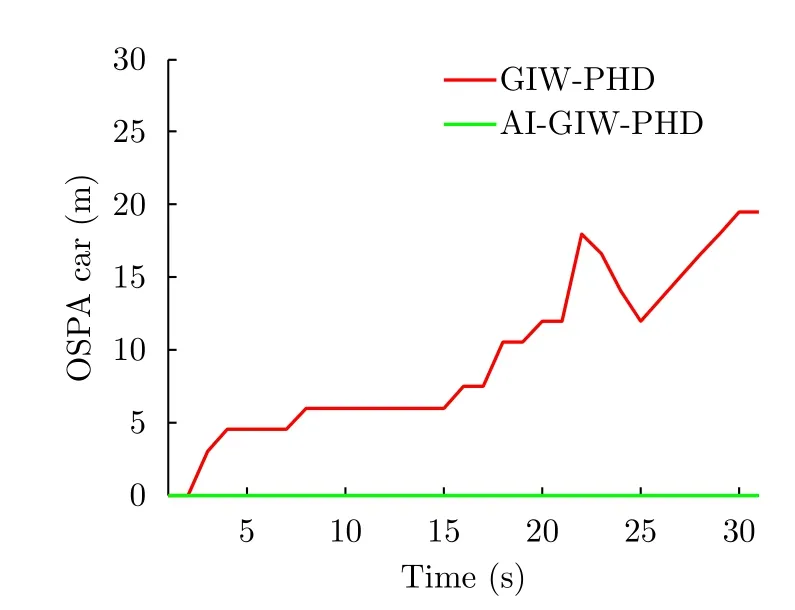
圖 9 平均OSPA勢誤差(SCR=13 dB)Fig. 9 Averaged OSPA cardinality error (SCR=13 dB)

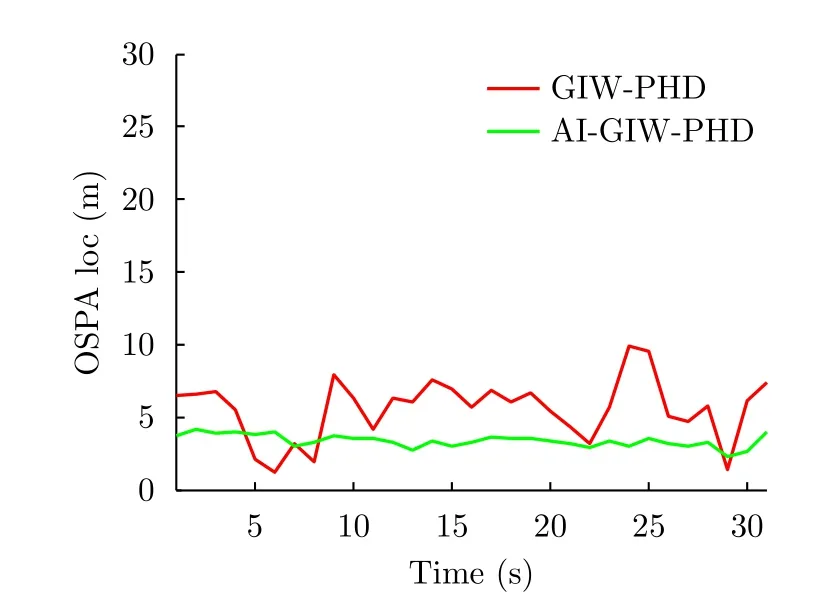
圖 10 平均OSPA位置誤差(SCR=6 dB)Fig. 10 Averaged OSPA location error (SCR=6 dB)

圖11 為SCR=6 dB時GIW-PHD和AI-GIW-PHD經過20次仿真后得到的平均目標數目估計值。可以看到，在低SCR條件下，GIW-PHD由于受到雜波的干擾導致目標數目估計始終存在很大的誤差，而AI-GIW-PHD在大部分時刻保持了對目標數目的準確估計，僅在倒數第2幀出現了比較明顯的偏差。

圖12為SCR=6 dB時GIW-PHD和AI-GIW-PHD經過20次仿真后得到的平均OSPA勢誤差。可以看到，與圖11顯示的結果一致，AI-GIW–PHD在目標數目估計方面顯著優于GIW-PHD。

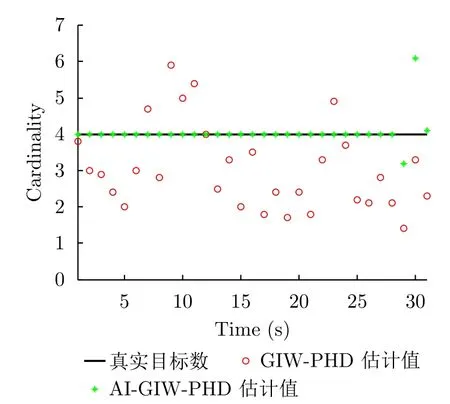
圖 11 平均勢估計結果(SCR=6 dB)Fig. 11 Averaged cardinality estimation (SCR=6 dB)

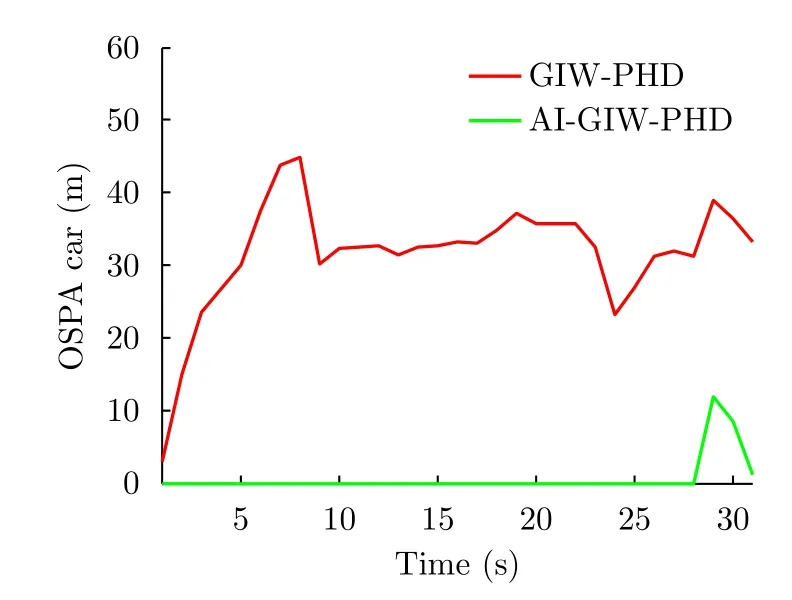
圖 12 平均OSPA勢誤差(SCR=6 dB)Fig. 12 Averaged OSPA cardinality error (SCR=6 dB)

5 結束語

GIW-PHD擴展目標濾波器在進行量測劃分和狀態估計時都只利用了量測的空間信息，在雜波密集環境下狀態估計和勢估計性能不佳。為解決這一問題，提出了結合幅度信息的GIW-PHD濾波器，利用量測的幅度信息來區分相距較近的目標和雜波量測，賦予目標量測單元更高的似然值，從而提升目標GIW項的權重，降低雜波的影響。在計算量測單元的中心時采用幅度加權的質量中心取代僅包含空間信息的幾何中心，從而進一步降低雜波的干擾。仿真結果表明，所提算法對擴展目標的勢估計性能顯著增強，在低信雜比環境下的狀態估計性能明顯優于GIW-PHD濾波器。但是，計算幅度似然會在一定程度上增加算法的運算成本。