危機下匯率市場與股市間的風險傳染效應研究

李逸卓 楊瀟

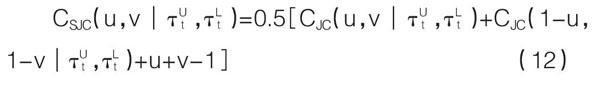
【摘 要】 當前各金融市場之間的聯系日益深入，使得他們之間發生風險傳染事件的概率顯著提高，因而有必要厘清各金融市場之間的相依關系，以防范金融風險在各金融市場之間的傳染，維護金融穩定。文章運用ARMA-GJR模型對市場風險因子進行濾波，針對風險因子的有偏胖尾分布特征，運用GPD的全參數極值模型對風險因子的尾部進行建模，隨后基于時變SJC-Copula模型，分析中國匯率市場與股票市場間的風險傳染。實證結果表明，中國股票市場與匯率市場之間更傾向于具有對稱的相依性;在尾部風險傳染上具有非對稱效應，且下尾的傳染效應強于上尾的傳染效應。

【關鍵詞】 風險傳染效應; 時變SJC-Copula; EVT; ARMA-GJR模型

【中圖分類號】 F830? 【文獻標識碼】 A? 【文章編號】 1004-5937（2020）18-0054-06

在經濟全球化的今天，國與國間的貿易往來日趨密切，各國之間的資本流動日益頻繁，使得各國外匯市場飛速發展。伴隨迅猛發展的信息科技，進一步深化金融市場間的聯系，大大提高了金融市場之間風險傳染概率。股票市場作為經濟的晴雨表、企業融資的重要渠道，不僅反映經濟的發展狀況，而且對推動經濟發展亦有舉足輕重的作用。因此，探究匯率市場與股市之間相依結構，考察兩者之間的風險傳染效應有著重要的經濟和現實意義。

目前，研究金融市場風險傳染效應的方法主要有四種：Granger因果檢驗理論、多元GARCH族模型檢驗、相關系數檢驗和Copula相依結構檢驗算法。前三種檢驗方法存在假定資產相關性服從線性相關和收益率服從正態分布等不足，在實際情形下，金融資產的特征主要為自相關、非對稱以及波動聚集等，通常為偏態分布，同時金融市場是十分復雜的動力系統，資產的相關結構具有顯著的非線性特征[ 1 ]。Copula函數具有不需要假定時間序列便能刻畫序列間非線性關系的優點，深受金融界學者的推崇。

不同的Copula函數具有不同的數學特征，因而對金融資產相關結構刻畫不盡相同。橢圓的Copula函數，如正態Copula函數和t-Copula函數能夠捕獲資產間的對稱性相關結構;阿基米德Copula函數，如Gumbel-Copula函數和Clayton-Copula函數分別能夠捕獲上尾相依結構和下尾相依結構;SJC-Copula函數能夠同時捕獲資產上尾相依結構和下尾相依結構，因而SJC-Copula函數通常被學者用來刻畫金融資產間的尾部相依結構。尾部相依結構之所以被投資者及金融風險管理者所重視，是由金融資產分布的尾部特性所決定的。金融資產分布的尾部，通常代表發生概率較小，然而一旦發生便會給投資者及風險管理者帶來巨大損失的風險事件[ 2 ]。于是，探究匯率市場與股市之間的尾部風險傳染就成為本文分析的重點所在。由于Copula函數均為靜態函數，換言之，即資產間的相依結構不隨時間的變化而變化，這顯然與復雜多變的金融資產間相依結構的實際情況不符，因而，學者提出時變的Copula函數來準確刻畫金融資產間時變的相依結構，以克服靜態Copula函數在刻畫相依結構上與實際不符的缺陷。如Wang等[ 3 ]運用時變Copula函數考察了中國股市與國際股市之間的動態相依結構;Zhu等[ 4 ]運用時變Copula函數考察了原油價格與亞洲太平洋地區股市之間的動態相依性。他們的研究得出時變SJC-Copula在捕獲金融資產尾部相關性方面具有良好的表現。因此，為考察危機背景下，匯率市場與股市之間的風險傳染效應，尤其是尾部風險傳染效應，本文選擇時變的SJC-Copula函數。

當前，基于時變SJC-Copula函數刻畫金融風險傳染效應已經展開了大量研究，并且取得較好成果[ 5-6 ]。但這些研究集中分析股票市場、原油市場和債券市場三者間的相依結構，對股票與外匯市場間相依性研究尚未開展。目前，有學者運用其他方法和理論，研究股票與外匯市場間的相關性。謝赤等[ 7 ]運用小波分析方法、張平等[ 8 ]運用Copula-AR-GJR-t模型、汪冬華和索園園[ 9 ]從多重分形理論角度、肖云湘和李星野[ 10 ]運用W-VAR-MGARCH-BEKK模型以及熊正德等[ 11 ]運用小波多分辨的多元BEKK-GARCH（1，1）模型深入研究了匯率與股市間的波動溢出效應。就目前來看，基于時變SJC-Copula函數分析股市與外匯市場間相依結構很少有人開展研究，因此將時變SJC-Copula函數運用于該領域將會得到一些新的結論。本文引入極值理論（EVT）刻畫市場風險因子的尾部特征，從而能夠更加準確地分析尾部風險傳染。

一、分析方法

（一）建立市場風險因子邊緣分布計算模型

研究外匯市場與股市之間的風險傳染效應，建立市場風險因子邊緣分布計算模型。一般情形下是基于對資產取對數的方法來計算收益率rt描述資產風險因子：

假設收益率rt服從式（2）：

式中，■t是資產收益率條件均值，■t是資產收益率條件標準差，zt是均值等于0、方差等于1的獨立同分布隨機變量。因此，對收益率rt的刻畫，就簡化成對條件均值■t以及條件標準差■t的刻畫。針對收益序列的波動聚集、自相關、“杠桿效應”和有偏胖尾分布等特征，基于ARMA模型刻畫收益率rt的條件均值，以刻畫收益率序列的自相關性;運用GJR模型來刻畫收益率的條件方差■2t，以刻畫收益率序列的波動聚集性及“杠桿效應”;同時引入EVT對收益率的尾部進行刻畫，以準確刻畫收益率尾部的有偏胖尾分布特征，進而為后續的尾部風險傳染效應分析提供良好的基礎。因此，本文運用ARMA（1，1）-GJR（1，1）對收益率rt進行建模分析，其形式如下：

同時，基于GPD的全參數極值模型刻畫收益率的尾部特征。rt只有近似在獨立同分布情況下，才能運用EVT刻畫收益率尾部特征，現實中，zt（■t=（rt-■t）/■t）滿足該要求[ 2 ]。因此，基于條件均值■t和條件方差■2，本文計算得到zt，基于GPD理論對zt建模，設為閾值，y為z-，則y為GPD分布，得到式（4）：

圖4為兩市場的尾部時變相依性用圖，能夠更加清晰地描述上證綜指及人民幣兌美元匯率間尾部相依結構。

由圖4可知，上證綜指和人民幣兌美元匯率間的上尾相關系數幾乎為0，屬于獨立分布，但是，與上尾相關系數相比，下尾相關性高于上尾，表明上證綜指和人民幣兌美元匯率同時出現暴跌事件概率要高于兩者同時出現上漲事件的概率，即人民幣兌美元匯率大幅下跌時，上證指數暴跌事件的概率要大大高于人民幣兌美元匯率大幅上升時上證指數暴漲事件概率。所以，提前做好預案，降低匯率市場風險傳染股票市場的概率十分重要，以保證股市穩定，促進經濟發展。

三、結論

為考察中國匯率市場與股票市場間的風險傳染效應，本文選取上證綜指和人民幣對美元匯率分別作為中國股票市場和中國匯率市場的代表，并運用ARMA-GJR模型對兩市場風險因子進行濾波，從而提取出標準收益率，并在此基礎上運用基于GPD的全參數極值模型對標準收益率的尾部進行建模，以刻畫風險因子的有偏胖尾分布特征，進而再運用時變SJC-Copula模型來考察兩市場間的風險傳染情況，所得結論主要有以下三點：

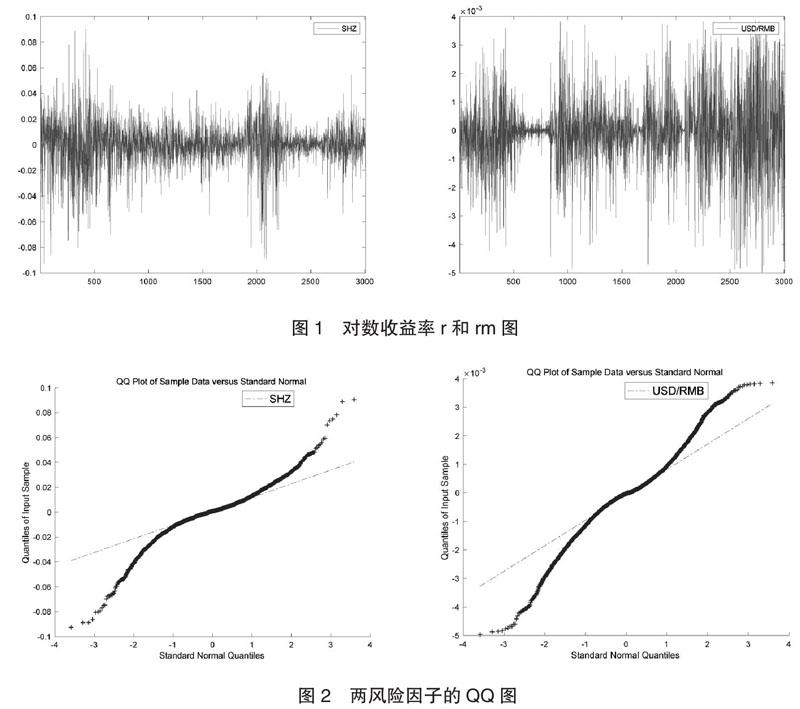
一是兩市風險因子具有非正態分布的偏胖尾特征，基于GPD模型的尾部建模可以較為準確地刻畫兩者間風險因子的尾部分布特征。

二是中國匯率市場與股市間存在著對稱的相依結構。在資料分析中，基于時變Copula模型（時變T-Copula模型和時變Frank-Copula模型），在刻畫市場間相依結構方面，明顯優于可以刻畫序列間非對稱相依結構的時變Copula模型。

三是中國匯率市場與股市間在尾部的風險傳染效應中存在非對稱性特征。基于SJC-Copula函數刻畫兩市尾部風險傳染效應的結果可知，匯率市場與股市間尾部風險具有非對稱效應。具體來說，兩市場任意一市劇烈下跌時，另一市場發生同樣事件概率也會增加。所以，應注意在一市暴跌時做好預案，防止市場間風險傳染，以保證市場穩定和經濟持續發展。

【參考文獻】

[1] 盧方元.中國股市收益率分布特征研究[J].中國管理科學，2004，12（6）：18-22.

[2] MCNEIL A J， FREY R. Estimation of tail-related risk measures for heteroscedastic financial time series：an extreme value approach[J].Journal of Empirical Finance，2000，7（3）：271-300.

[3] WANG K，CHEN Y H，HUANG S W. The dynamic dependence between the Chinese market and other international stock markets：a time-varying copula approach[J].International? ?Review? ?of? ?Economics? ?& Finance，2011，20（4）：654-664.

[4] ZHU H M， LI R， LI S. Modeling dynamic dependence between crude oil prices and Asia-Pacific stock market returns[J].International Review of Economics & Finance，2014，29：208-223.

[5] 肖利平.中國債券市場與股票市場間波動溢出效應：基于SJC-Copula模型的分析[J].證券市場導報，2011（9）：57-66.

[6] 鐘明，郭文偉.基于SJC Copula模型的銀行業與房地產業動態相依性及其結構突變[J].系統工程，2014（8）：32-43.

[7] 謝赤，張麗，孫柏.外匯市場與股票市場間波動溢出效應：基于匯改后數據的小波多分辨分析[J].系統管理學報，2012，21（1）：13-21.

[8] 張平，胡根華，孟曉.匯改后匯市與滬深股市動態相依結構分析[J].財會月刊，2013（22）：17-20.

[9] 汪冬華，索園園.金融危機前后中國股票市場和外匯市場的交叉相關性：基于多重分形理論的視角[J].系統管理學報，2013，22（3）：394-491.

[10] 肖云湘，李星野.外匯市場與股票市場之間的溢出效應研究：基于W-VAR-MGARCH-BEKK模型的分析[J]. 南方金融，2014（2）：59-64.

[11] 熊正德，文慧，熊一鵬.我國外匯市場與股票市場間波動溢出效應實證研究：基于小波多分辨的多元BEKK-GARCH（1，1）模型分析[J].中國管理科學，2015（4）：30-38.

[12] DANIELSSON? J， VRIES? C? G. Value-at-risk? and extreme returns[J].Annalesd' Economieet de Statistique，2000：239-270.

[13] PATTON A J. Modeling time varing exchange rate dependence using the conditional copula[Z].San Diego，Department of Economics，University of California，2001.

[14] 許祥云，廖佳.宏觀經濟環境、匯率政策目標和東亞貨幣與人民幣匯率波動關系的非對稱性：基于金融危機前后的比較分析[J].經濟經緯，2015（5）：43-48.