心動 手動 思動

周玉燕

思維是數學能力之“核”，思維也是數學素養(yǎng)之“魂”。開展深度教學，提升學生思維品質是數學教育工作者的共同目標。那么如何通過課堂教學，讓思維的種子在學生的心里悄悄扎根，并不斷生長呢？下面，以《真分數和假分數》的磨課經歷為例，談談自己的幾點看法：

一、心動——富有挑戰(zhàn)，直擊困惑

對于較高年級的孩子來說，真正能激發(fā)他們學習興趣，勾起他們求知欲望的往往不是有趣的童話故事，也不是各種兜圈子的文字游戲，而是能夠直擊他們困惑點的數學問題。

以《真分數和假分數》一課為例，最先設計的課堂導入是這樣的：

師：會數數嗎？

生：會，1、2、3、4……12，（師課件演示12根小棒）

師：12根小棒，既可以看做12個一，也可以看做1個十和2個一。

師：（出示一個圓）如果把這個圓平均分成4份，其中的一份是（ ），兩份是（ ）接著數 、 、 、 ……（學生數得熱熱鬧鬧卻一臉茫然）

反思：這樣的課堂導入讓學生動口，卻沒辦法讓學生動心。因為缺乏明確的問題導向，也缺乏足夠的挑戰(zhàn)性。

修改后的課堂導入：

師：這節(jié)課我們要一起學習《真分數和假分數》，你們聽說過真分數和假分數嗎？對它們有哪些了解？

生：我知道分子比分母小的叫真分數，分子和分母一樣大或分子比分母大的叫假分數。真分數小于1，假分數大于1……

師：你們知道的可真不少，對于真分數和假分數，還想知道什么？

生：假分數是分數嗎？為什么分數要分真假？假分數假在哪里？……

幾句談話就把學生已有的知識經驗和困惑點都呈現了出來，為后續(xù)的教學指明了方向。同時，因為后面的教學是基于學生提出的問題而展開的，學生的興趣高漲，心動是必然的。

二、手動——手腦并用，促進發(fā)展

我們重視直觀教學，重視動手操作能力的培養(yǎng)，但直觀不應以降低思維含量為前提，動手操作更不應等同于手工課。任何直觀教學都應有利于促進思維的發(fā)展，而不是拉思維的后腿。

仍以《真分數和假分數》一課為例，一開始的動手操作環(huán)節(jié)是這樣設計的：

師：同桌合作，把你們分到的扇形擺一擺，拼一拼，并用分數表示出來。

經過五六分鐘的拼接，學生拼出了 、 、 ……

反思：教具很精美，孩子們似乎也拼得很開心。他們輕而易舉就拼出了各種假分數，并能說出 是由8個 組成的， 是由13個 組成的……。但是，分數的組成是難點嗎？這樣的動手操作需要思考嗎？通過操作活動能促進學生對 的理解嗎？答案都是否定的。

修改后的動手操作環(huán)節(jié)：

師： 表示什么呢？

生： 表示把單位“1”平均分成4份，取其中的5份。（根據分數的意義很順溜地說出來了）

師：平均分成4份，取5份？（師假裝一臉困惑，學生也個個傻眼了）

師：到底是怎么回事呢？想一想，把你對 的理解用文字或者圖形的方式表達出來。

學生陷入了沉思，之后陸陸續(xù)續(xù)畫出了對于 的理解。

盡管沒有絢麗的學具，也沒有熱熱鬧鬧的小組合作，但我們明顯地感覺到：孩子動手前陷入了沉思，動手時全神貫注。之后組織的交流與辨析活動更充分暴露了他們思維的亮點和盲點。顯而易見，這樣的動手操作讓學生的腦子真正地動了起來，手腦并用使思考更深入，思維也得到了相應的發(fā)展。

三、思動——上通下達，提升品質

無論是激發(fā)學生學習興趣，還是借助幾何直觀加深學生對知識的理解，歸根結底都是為了更有效地促進學生思維的發(fā)展。因此，在解決完具體問題之后，教學不該戛然而止，而是應或溯本求源、或順流而下，進一步拓寬視野，提升思維品質。

如《真分數和假分數》最后一個環(huán)節(jié)原先的設計：

師：在數軸上標出 、 、 、 的位置。

學生找到各個分數在數軸上的大概位置（因0到1之間的線段難以平均分成3、4、5、6份）

師：看來每個分數都能在數軸上找到自己的家，數軸上的每個點都有一個與之對應的分數。

師：觀察數軸，你發(fā)現了什么？

學生的發(fā)現五花八門，有的發(fā)現分母各不相同，有的比較各分數的大小，有的比較各分數和1的關系……

反思：利用分數的意義在數軸上找出各個分數的位置，與之前的教學基本平行，學生的關注點很分散，既沒有挖掘知識的深度也沒有拓寬認識的廣度。

修改后的環(huán)節(jié)：

師：如果把 放在數軸上，應該放在哪里？

生：放在1和2之間，把1和2之間的線段平均分成4份， 在1右邊一份的位置。

師：你還能找到分母是4的其他分數嗎？

生：在0和1之間平均分成4份，一份是 ，兩份是 、 ……

師：觀察這些分數的位置，你發(fā)現了什么？

生：我發(fā)現真分數都在1的左邊，都小于1，假分數在1或者1的右邊，大于或等于1。

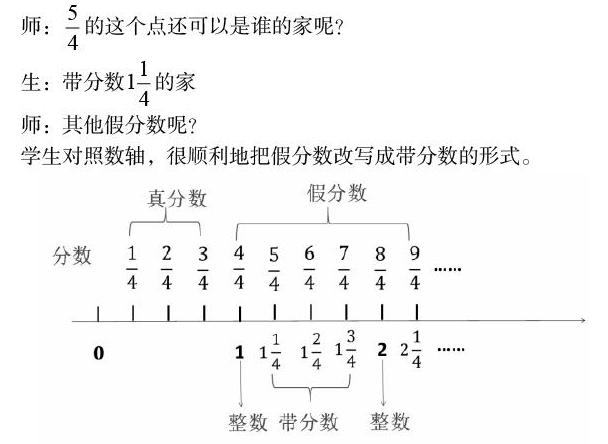
師： 的這個點還可以是誰的家呢？

生：帶分數 的家

師：其他假分數呢？

學生對照數軸，很順利地把假分數改寫成帶分數的形式。

兩次教學都用到數軸，第一次學生的思維仍停留在從分數的意義出發(fā)找到各分數位置的層次上，知識是分散、割裂的。第二次教學則利用數軸，聚焦分母是4的分數，引導學生自主發(fā)現真分數、假分數、帶分數和整數之間的聯(lián)系。學生站在“數”的高度上，把真分數、假分數、帶分數納入已有的數的體系內，擴充了對數系的建構，也提升了思維的深度和廣度。

通過此次磨課，我們真切地感受到：富有挑戰(zhàn)性的數學問題是激發(fā)學生求知欲，啟動思維引擎的首要前提;思而不得時的手腦并用、數形結合，是突破思維瓶頸的重要手段;解決完問題之后的上通下達，左顧右盼則是提升思維品質的必經之路。