抓關鍵 巧解題

王娟玲

“統計與概率”與我們的生活密不可分。如果我們在生活中學會用數學的眼光來分析問題，就會發現很多樂趣。不信，我們就一起來看看。

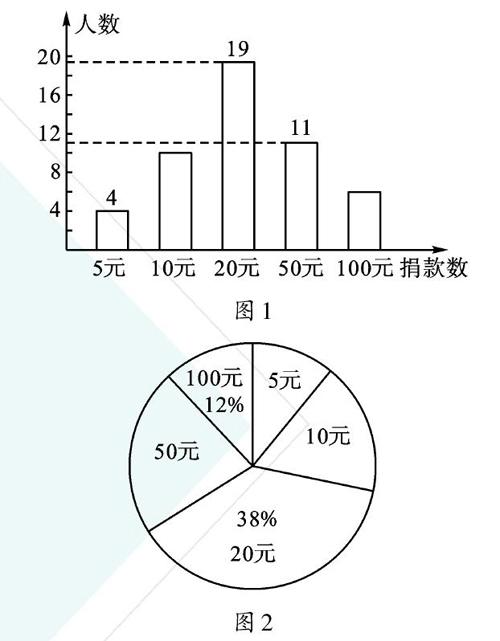
例1在一次捐款活動中，某班50名同學都拿出自己的零花錢，有捐5元、10元、20元的，還有捐50元和100元的，如圖所示的統計圖反映了不同捐款數的人數比例。那么根據圖中信息，該班同學平均每人捐款_____元，捐款的眾數是_____元，中位數是_____元。

【分析】本題的關鍵是：根據圖1中捐款20元的人數是19人和圖2中捐款20元人數占總人數的38%解決問題。求得總人數：19÷38%=50（人）。進而求得捐款100元的人數：50×12%=6（人）。最后求得捐款10元的人數：50-（4+19+11+6）=10（人）。平均每人捐款數=總金額÷總人數。同學們要避免將5個數的算術平均數認為平均每人捐款數。根據眾數的定義，捐款的眾數為20元。在求解中位數時，一定要牢記將數據先排序。總人數為50，中位數取的是第25和第26人捐款面值的平均數，這兩個同學捐款數均為20元，所以中位數也是20元。

答案：33，20，20。

例2一只不透明的袋子中裝有2個白球和3個紅球，這些球除顏色外其他都相同，攪勻后從中任意摸出1個球。

甲說：“摸出的球不是白球就是紅球，所以摸出白球和摸出紅球這兩個事件是等可能的。”

乙說：“白球有2個，紅球有3個，所以摸出白球和紅球這兩個事件不是等可能的。”

你認為誰的說法有道理，請說明理由。

【分析】本題關鍵在于對“等可能性事件”的理解。袋子里共有5個球，所以摸出每個球是等可能的。由于有2個白球和3個紅球，所以乙的說法正確。

解：乙有道理，摸到每一個白球和每一個紅球是等可能的，摸出白球的可能性比摸出紅球的可能性小。

例3甲、乙兩超市（大型商場）同時開業，為了吸引顧客，都舉行有獎酬賓活動：凡購物滿100元，均可得到一次摸獎的機會。在一個紙盒里裝有2個紅球和2個白球，除顏色外其他都相同，摸獎者一次從中摸出兩個球，根據球的顏色決定送禮金券的面值（在該超市使用時，與人民幣等值），如下表：

如果只考慮中獎因素，你將會選擇去哪個超市購物？請說明理由。

【分析】理清題意，選擇去某個超市購物的原因在于平均獲得的禮金券面值多，這就需要我們計算摸到各種球對應的概率。根據題意，每個人摸兩個球，關鍵是“無放回”，即第一次摸到的球，第二次不會再摸到，再根據獲得的禮金券計算平均收益即可。

解：根據題意畫出樹狀圖，如下：

所以我會選擇去甲超市購物，因為在甲超市獲得禮金券的平均收益多。

解決概率問題時，我們要從概率的意義出發，理解等可能性事件。畫樹狀圖或列表前更要讀懂題意，抓關鍵詞，從而巧妙地解決問題。

（作者單位：江蘇省無錫市東實驗學校）