一種基于聚類分析的二維激波模式識別算法

2020-09-10 03:25:34常思源白曉征劉君

航空學報 2020年8期

常思源，白曉征，劉君

大連理工大學航空航天學院，大連 116024

激波的探測與可視化是計算流體力學(CFD)領域中一個非常富有挑戰的問題。在某些流場參數的等值線云圖中，通常認為激波間斷位于大量等值線聚集處，但對于存在接觸間斷、膨脹波和旋渦等復雜波系干擾的流場，該方法很容易對激波產生誤判，因此有必要發展更加精準的激波探測(Shock Wave Detection)技術。

至今，很多學者[1-14]基于激波捕捉(Shock-Capturing)法計算出的流場提出了各種各樣激波探測的方法。1985年，Buning和Steger[1]首次提出將沿激波法向(近似用壓強梯度方向代替)馬赫數等于1的等值面視為激波面；該方法隨后被Darmofal[2]稱為基于正則馬赫數(Normal Mach Number)的激波探測法，并逐漸在流場可視化中被廣泛應用；Liou等[3]在此基礎上介紹了3種濾波技術，以剔除辨識出的偽激波；隨后，Lovely和Haimes[4]又成功將其推廣到非定常流動中用以探測運動激波。1993年，Pagendarm和Seitz[5]詳細地介紹了一種基于流場密度方向導數(Directional Derivative)來辨識激波的方法，即將密度二階方向導數為0的等值面視為激波陣面，并結合密度的一階方向導數(密度梯度在當地速度矢量上的投影)來過濾噪點；其后，Ma等[6]的數值算例表明基于正則馬赫數過濾噪點可能會獲得更好的結果。1994年，Van Rosendale[7]提出了一種針對二維非結構網格的激波擬合算法，通過比較網格節點之間的密度梯度來移動網格使其邊緣與激波線對齊；Ma等[6]認為該算法中局部加權密度梯度的策略可以用于識別出激波附近的網格節點，但可能需要結合其他流場特征來實現更準確的辨識。2011年，Kanamori和Suzuki[8]巧妙地將特征線理論(Theory of Characteristics)運用于二維激波探測中，并成功推廣到非定常[8]和三維流場[9]計算中，相比前述方法，該算法雖然較為復雜，但不需要人為設置一些經驗性的閾值參數進行濾波就可以獲得更加良好的結果。2017年，Akhlaghi等[10]通過分析數值紋影圖內某些流動參數的高斯分布(Gaussian Distribution)，提供了一種新的激波辨識方法，對連續流和稀薄流都比較適用。近年來還有學者[11-12]嘗試將深度學習(Deep Learning)融入大規模流場的激波識別中，取得了不錯的結果。

國內針對激波探測的研究報道相對較少，馬千里等[13]基于壓強梯度計算正則馬赫數，并利用激波物理特征，結合光線投射法提出了一種基于兩級采樣的多激波提取方法。2013年，Wu等[14]在其綜述中總結了以往激波辨識方法，并指出了對運動激波和弱激波的精確識別是非常有挑戰的研究方向。

整體來看，以上這些激波探測法具有一個共同的特征，即它們都是基于“當地標準(Local Criteria)”進行辨識的；也就是說，激波位置的識別僅通過分析局部一個網格節點/單元(最多考慮一層相鄰網格)上的流動參數來實現。Paciorri和Bonfiglioli[15]認為這些探測技術的當地性質正是其局限性和缺陷的根源。一方面，這些方法往往將探測到的一系列散點[6]或小線段[8-9]視為激波線/面，但由于數值耗散和振蕩，這些激波線/面處經常會出現噪聲、偽激波分支或空隙[14]。另一方面，所有這些算法都不能判斷出流場中是否存在激波干擾點，即不能清晰地給出流場中激波干擾的模式，如λ激波、異側激波相交、激波-壁面反射等。

近年來，有一批學者[16-19]重新開啟了激波裝配(Shock-Fitting)法的研究與應用，相比當前主流的激波捕捉法，該方法必須顯式地處理激波，因此在開始計算前，通常都需要從激波捕捉流場獲取相關信息，如合理的初始流動參數、激波的近似位置、激波的干擾結構等。然而，由于上述激波探測法的缺陷，其很難直接用于激波裝配的初始化中[15]，最終造成這些激波裝配算法難免需要依據先驗知識進行人工干預來設置初始激波及激波干擾點的位置。

針對上述問題，Paciorri和Bonfiglioli[15]于2012年介紹了一種二維激波模式識別技術，首先根據傳統基于當地密度二階方向導數的方法[6]提取出激波點云，隨后利用霍夫變換(Hough Transform)搜尋這些散點中的特征直線并去除噪點，再采用最小二乘(Least-Squares)法擬合得到各條激波曲線，最后通過一套模糊邏輯(Fuzzy Logic)算法識別出激波干擾的模式。然而，該方法實施起來比較繁瑣，對于流場中長度較短的激波分支容易產生誤判，且很難適用于非定常流場。

本文提出了一種面向全局(Global)的二維激波模式識別算法，對探測出的激波帶網格單元進一步處理，通過聚類分析(Cluster Analysis)方法將激波單元劃分成許多簇；分析各個簇的相鄰關系就可以清晰地判斷出激波干擾的模式，最終基于Bézier曲線擬合算法優化的激波線和數值捕捉的激波相比在形狀和位置上都較為吻合。該算法不僅邏輯簡單，且不受網格類型的限制，同時在非定常流動中也具有較高的可靠性。

1 二維激波模式識別算法

結合一個定常無黏激波反射算例(幾何模型和流場如圖1所示，其中p表示壓強，下標∞表示來流狀態)，從3個主要方面介紹了該二維激波模式識別算法的步驟和特點。在該算例中，來流馬赫數Ma∞=1.5，楔角θ為10°，入口和出口高度分別為2.17L和2L。入射斜激波S1在上壁面發生馬赫反射產生了強度較強的馬赫干擾S2，而反射激波S3經膨脹波異側干擾后強度下降，最后在下壁面產生了正規反射，次反射激波S4與出口邊界相交。此外，雖然該流場是基于均勻的非結構三角形網格(網格尺寸Δ=0.015L)計算的，但是該識別算法同樣適用于結構網格、混合網格和非均勻網格等，在2.2節有相關描述。

1.1 辨識激波單元

本文算法是針對網格單元而非網格散點實現的，因此首先需要從圖1所示流場提取出表征激波位置的網格單元，即圖2所示激波單元。考慮到引言所述若干激波探測方法的適用性和魯棒性，本文基于流場單元格心的壓強梯度，設計了一套針對激波的辨識準則，具體步驟為

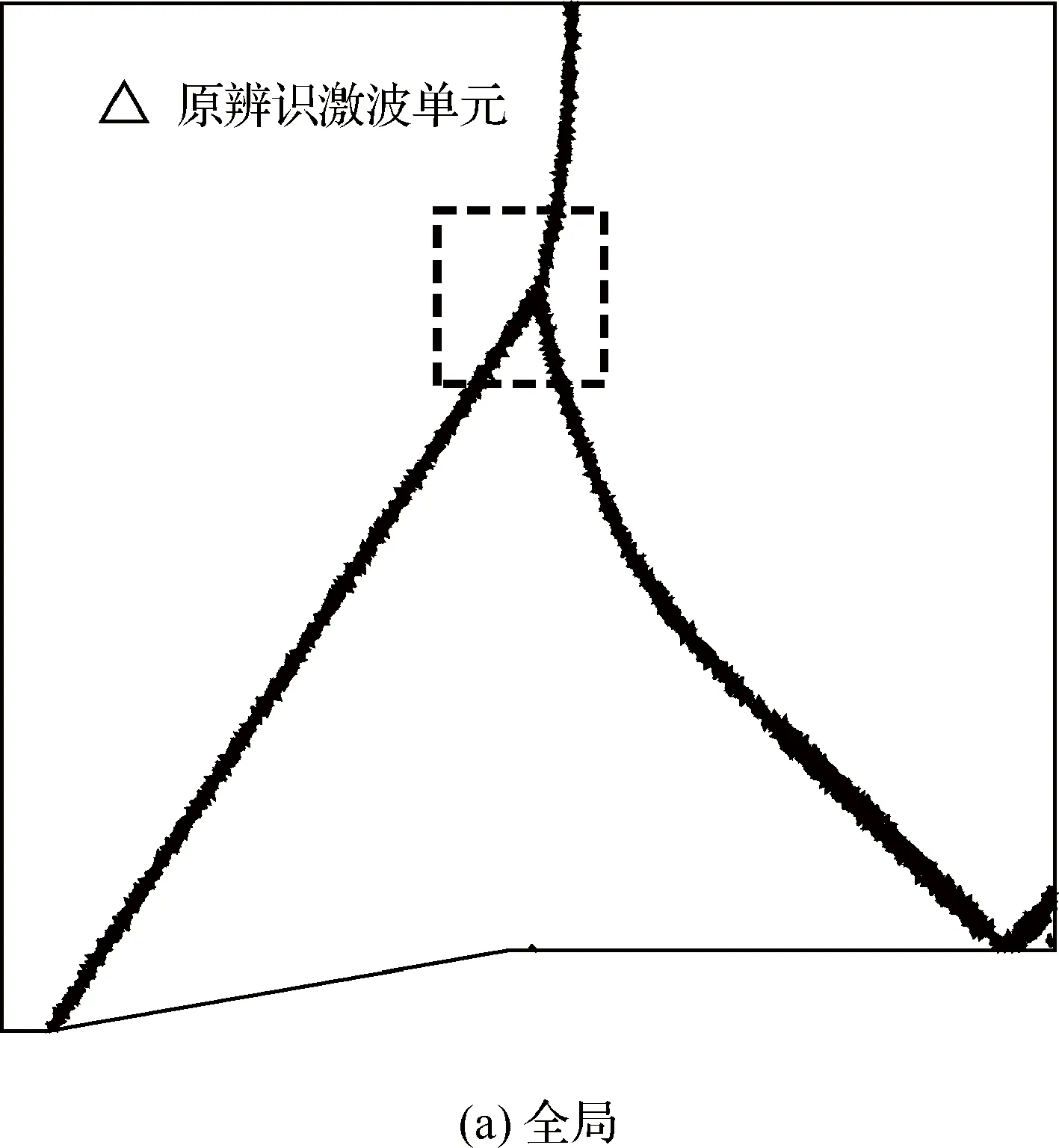
圖2 定常激波反射：初始辨識的激波單元

(1)

由于考慮了流向，δp的正、負號分別對應流體處于壓縮和膨脹的狀態，而激波處通常表現出很強的壓縮性，因此首先要過濾掉δp<0的單元。

2) 由于數值計算難免會存在耗散和誤差，會造成一些非激波區域的δp值為一個較小的正量，故過濾掉滿足式(2)的單元：

δp<ξ1δpmax

(2)

式中：δpmax為流向壓強梯度的全場最大值；ξ1為全局濾波系數，當流場中激波的強度比較懸殊時，該系數過大可能會濾掉某些弱激波而導致部分激波帶缺失，因此經大量數值試驗的調試，取ξ1=0.01。流場中除了激波間斷外可能還存在接觸間斷，由于數值捕捉出的接觸間斷兩側壓強近似相等，因此基于式(2)流向壓強梯度閾值法可以有效地過濾掉接觸間斷。

3) 然而幾乎不可能只通過設置滿意的ξ1，既能完整地辨識多激波又能去除全部噪聲。此外，因全局濾波強度不大，經第2步辨識的激波帶可能會出現一些偽激波單元，為了在一定程度上提高辨識方法的普適性，考慮局部特性對滿足式(3)的單元進行二次去噪：

(3)

定常激波反射算例經上述方法辨識出的具有一定厚度的“激波帶”如圖3所示，受激波強弱影響，激波帶的厚度并不均勻，通常有2～5層激波單元。由于數值誤差的存在，激波帶往往存在很多“毛刺”和“空穴”，為了使后續聚類分析更加準確，從兩方面對原始辨識的激波帶進行了光順優化。首先一方面標記“空穴單元”為激波單元，另一方面剔除“毛刺單元”。所謂空穴單元是指其所有節點均落在激波帶上的初始非激波單元(圖3中綠色單元)，而毛刺單元是指共面相鄰激波單元的個數小于2的初始激波單元(圖3中藍色單元)。

圖3 定常激波反射：激波帶的優化

1.2 激波單元的聚類分析

聚類分析是一種十分重要的統計數據分析方法，在數據挖掘、模式識別、圖像分析和機器學習等許多領域受到廣泛應用；它的目標是將數據集分成許多簇，使得同一簇內的數據點相似度盡可能大，而不同簇間的數據點相似度盡可能小[20]。本文采用經典的K-means聚類(K-Means Clustering)[21]算法對優化后的激波帶進行聚類處理，下面舉例簡要介紹該算法對圖4(a)數據點的聚類流程：

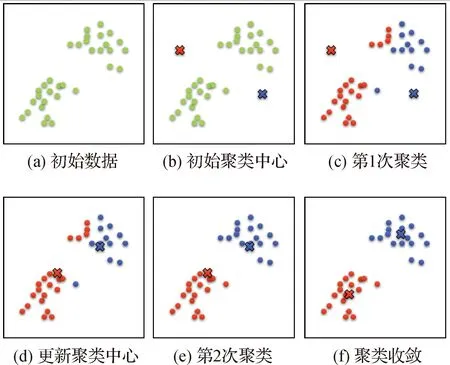
圖4 K-means聚類算法示意圖

1) 選擇K個初始“聚類中心”。在圖4(b)中，初始化選擇了兩個聚類中心，即圖中紅、藍“×”形點。

2) 對任意一個數據點，求其到K個聚類中心的“距離”(取歐氏距離)，將該數據點歸到距離其最近的聚類中心所在的“簇”。如圖4(c)所示，所有數據點在經過第一輪遍歷后被分為紅、藍標識的兩個簇。

3) 利用均值等方法更新K個簇的中心值。此時對當前標記為紅色和藍色的數據點分別求出其新的質心，作為新的聚類中心，如圖4(d)所示，紅色和藍色聚類中心的位置發生了變動。

4) 重復步驟2)～3)，若所有聚類中心在迭代更新后位置都保持不變，則迭代結束；否則繼續迭代。最終得到的兩個簇及其聚類中心如圖4(f)所示。

K-means聚類算法操作簡單，易于實現，且十分高效，一般僅需5～10次迭代即可收斂。但是研究表明，該算法對初始聚類中心的位置選取比較敏感，不同的隨機初始聚類中心得到的聚類結果可能差異顯著。因此，在對激波單元聚類時，合理的初始聚類中心位置顯得至關重要，其既不能偏離激波帶過遠，也不能分布的過密或過稀。下面介紹下針對激波帶初始聚類中心的選取方法。

首先任意選取一激波單元作為搜索起點，以該單元格心為圓心，n倍當地網格尺寸為半徑r作“搜索圓”(經大量算例評估，一般n取6～7即可獲得合理的結果)，如圖5所示；隨后將格心點落在該圓區域內且未被搜尋到的激波單元歸為一簇，計算該簇中所有激波單元格心坐標的平均值，作為新的搜索圓圓心坐標；反復迭代直到所有激波單元均被搜尋到，則所有搜索圓的圓心即為初始聚類中心。

圖5 定常激波反射：確定初始聚類中心

取所有激波單元的格心作為數據點集，對所有激波單元進行K-means聚類；經過若干次迭代后最終所有激波單元被劃分到不同的簇，如圖6所示，為方便顯示，緊鄰的簇用不同顏色加以區分。

圖6 定常激波反射：K-means聚類結果

為了后續便于分析激波拓撲結構及其干擾模式，根據每個簇的相鄰特征將簇進一步分成4類：

1) 終止簇。若流場內部某簇僅有1個相鄰簇，則該簇為終止簇；其一般位于流場內部激波起始/終止處，注意該簇不與邊界相鄰。

2) 普通簇。若流場內部某簇僅有2個相鄰簇，則該簇為普通簇；其一般呈“串狀”普遍分布于激波帶中，是數量最多的簇。

3) 分叉簇。若流場內部某簇有3個及以上相鄰簇，則該簇為分叉簇；其一般分布于厚度較大的激波帶處，如三波點、四波點和弱激波處等。

4) 邊界簇。若某簇直接與流場邊界相鄰，則該簇為邊界簇；其通常存在于激波-壁面反射處、壁面拐角處以及流場進出口邊界處等。

其中，終止簇、分叉簇和邊界簇統稱關鍵簇，其在流場中個數雖少，卻往往位于激波拓撲或形狀發生變化的關鍵位置處。

1.3 激波的模式識別與擬合

如何自動準確地辨識出流場中激波干擾點的位置是一個難題。下面通過對激波帶K-means聚類得到的各個簇進行“近鄰分析”，給出了一種激波模式識別和激波線擬合的策略：

1) 判斷是否存在需要進行合并的簇。具體分兩方面，若某分叉簇與其他分叉簇相鄰，則將這些分叉簇合并；若某邊界簇與其他邊界簇(注意它們必須對應同一個邊界)相鄰，則將這些邊界簇合并。

2) 若進行了簇合并的操作，需要重新對簇進行分類，并計算新簇的聚類中心。如圖6(a)無需進行簇合并，而圖6(b)經簇合并后變成圖7，即原4個相鄰分叉簇合并后形成1個新的普通簇，一同緊靠下壁面的2個相鄰邊界簇合并后形成1個新的邊界簇。

圖7 定常激波反射：簇合并后

3) 識別關鍵激波點。規定若某分叉簇與周邊3個簇(見圖6(a))或4個簇(見圖23)相鄰，則該分叉簇對應的聚類中心即為三波點或四波點；若某分叉簇僅與1個簇相鄰，則其聚類中心即為激波終止/起始點(見圖25)；若某邊界簇與2個簇相鄰(圖7下邊界處)，則取該邊界簇對應的邊界中心點作為激波-壁面反射點；同理，若某邊界簇僅與1個簇相鄰(圖7右邊界處)，則邊界中心點即為激波-邊界干擾點。通過以上近鄰分析，便可識別出激波-激波干擾或激波-邊界干擾等模式。

4) 記錄各條激波所包含的簇。從第3)步得到的某一關鍵簇開始搜索，依次記錄下該分支上兩兩相鄰的所有普通簇，直至搜索到另一關鍵簇停止，此時該一系列簇即對應一條激波；繼續搜索確定下一激波分支上的簇，直到遍歷完流場中所有的簇。

5) 擬合激波線。依次連接激波包含的一系列簇所對應的聚類中心，便可得到各條激波線；然而此時得到的激波線可能比較曲折(圖7中的白色實線)，為此，本文進一步采用著名的Bézier曲線擬合算法[22]獲取更加光滑的激波線，下面對其作簡要介紹。

當給定一系列有序散點P0、P1、…、Pn時，則其n階Bézier曲線的一般參數化形式為

(4)

如4個點對應的三階Bézier曲線表達式為

B3(λ)=P0(1-λ)3+3P1λ(1-λ)2+

3P2λ2(1-λ)+P3λ3λ∈[0,1]

(5)

式中：Pi稱為Bézier曲線的控制點，且該曲線開始于點P0(對應λ=0)并結束于點Pn(對應λ=1)。值得注意的是，Bézier曲線是有方向性的，控制點的次序不同會擬合得到不同的曲線；且Bézier曲線是直線的充分必要條件是所有控制點共線。

因此，根據Bézier曲線的特點，若第4)步記錄的某條激波包含n+1個簇，則將兩個關鍵簇的聚類中心分別作為起始點P0和終止點Pn，而將其余依次緊鄰的普通簇的聚類中心作為控制點P1～Pn-1，進行n階Bézier曲線擬合便得到更加光滑的激波線，如圖8所示。

圖8 定常激波反射：擬合的激波線

圖9對比了最終擬合的激波線與流場壓強云圖，4條激波線、三波點、激波-壁面反射點和激波-邊界干擾點的位置都比較準確，顯示出該算法具有良好的有效性和準確性。

圖9 定常激波反射：激波線擬合結果與云圖對比

1.4 算法小結

該二維激波模式識別算法的總體流程如圖10所示，主要包含激波辨識、聚類分析和識別擬合3方面內容；此三者層層遞進，激波辨識是基礎，聚類分析是核心，而識別擬合是關鍵。

圖10 算法流程圖

從激波捕捉流場出發，通過流向壓強梯度閾值法進行二級濾波辨識提取出具有一定厚度的激波帶，到最終準確識別出激波-激波干擾點和激波-邊界干擾點等關鍵位置，且擬合出的各條激波線的形狀和位置都具有較高的精度。總之，該算法的最大優勢是基本不需要人工參與，且算法簡單高效，可以準確實現從“激波帶”到“激波線”的擬合識別。

2 算例驗證

通過4個超聲速流動算例從多方面考察了該算法的準確性、適用性和可靠性。以下激波捕捉流場均基于格心型有限體積法[23]計算，空間對流項通量采用van Leer格式，時間推進采用顯式4步Runge-Kutta格式，保證在光滑流場中時空均具有二階精度，全場均不考慮黏性。

2.1 定常斜激波

首先，采用兩種條件下的定常斜激波算例，驗證本算法最終擬合出的激波線的準確性。計算區域為x∈[0,L]，y∈[0,0.9L]，在x=0.1L處存在楔角，均勻超聲速來流經過楔面會產生一道筆直的斜激波，上邊界為超聲速出口，激波不會反射。為了產生相對較弱和較強的斜激波，楔面角θw分別取3°和20°，對應的來流馬赫數Ma∞分別為1.469和1.959。計算網格尺寸均為0.02L，全場分別有5 257個和4 472個三角形網格。

兩種狀態下的斜激波經辨識和聚類分析的結果如圖11所示，弱激波辨識出的激波帶較寬，最終一共得到25個聚類中心；而強激波辨識出的激波帶更加銳利，最終一共得到了22個聚類中心。將這些聚類中心作為控制點按順序代入式(4)擬合得到Bézier曲線，并與相應的理論值進行對比(圖12)，可見擬合值具有較高的位置精度。表1進一步對比了激波角，可見無論是弱激波還是強激波，最終擬合出的激波線的激波角度和理論值的相對偏差都不到1%。

圖11 定常斜激波：聚類結果

圖12 定常斜激波：激波線擬合值與理論值對比

表1 定常斜激波：激波角擬合值和理論值對比

2.2 定常激波反射

仍考慮圖1所示的定常激波反射流動，測試本算法對不同類型網格的可靠性。首先分別基于全場均勻的四邊形結構網格和三角形/四邊形混合網格重新進行數值計算，平均網格尺寸均為0.015L。圖13給出了這兩種類型網格下局部流場壓強等值線云圖(圖例與圖1一致)。

圖13 定常激波反射：不同種類網格下的壓強云圖

根據1.1節所述的激波探測方法，采用相同的濾波系數，分別獲得滿足條件的激波帶。在對激波單元進行K-means聚類分析時，結構網格算例全場一共確定了64個初始聚類中心，而混合網格算例共搜尋到了82個，經若干步后得到收斂的簇及其聚類中心。此時，根據簇的類別和相鄰簇的個數判斷某些簇是否需要進行合并，圖14和圖15分別給出了兩種網格下壁面馬赫反射處和正規反射處聚類合并后的結果。

圖14(a)和圖15(a)中各存在一個分叉簇，因其與周圍3個激波帶分支中的3個普通簇相鄰，可以判定該分叉簇的聚類中心位于流場三波點附近。此外，反射激波S3在受到膨脹波干擾后，強度顯著減弱；觀察圖14(b)和圖15(b)壁面激波反射處的激波帶，其厚度要明顯大于三波點附近激波帶的厚度，相應地，各簇包含的單元個數也明顯增加，但并沒有存在錯誤的分叉簇，且下壁面和出口邊界處的兩個邊界簇都被準確地識別出來。值得注意的是，由于激波-壁面反射點比較靠近出口邊界，圖14(b)中存在兩個邊界簇直接相鄰的情況，但由于它們鄰近的邊界不同，因此在簇合并操作中并未錯誤地將它們合并。

圖14 定常激波反射：基于結構網格的聚類結果

圖15 定常激波反射：基于混合網格的聚類結果

以上采用的都是均勻網格，下面進一步考察了本算法在非均勻網格中的適用性。如圖16所示，在非結構網格的基礎上，沿入射激波的法向進行加密，第一層網格高度為0.002L，向激波兩側各推進5層四邊形網格，網格高度增長率取1.2，隨后將激波右側四邊形網格沿對角線剖分成三角形網格。圖17顯示了對辨識出的激波帶進行聚類分析后的結果，雖然激波帶厚度差異明顯，但并不影響分叉簇的位置識別。

圖16 定常激波反射：非均勻網格下的壓強云圖

圖17 定常激波反射：基于非均勻網格的聚類結果

最后對比了以上3種網格下最終的擬合結果(圖18)，4條擬合激波線的形狀和位置都與數值捕捉的激波吻合得很好；從局部放大圖看出，三者擬合出的三波點和邊界干擾點位置稍有不同，這是由于流場數值誤差和初始激波帶辨識差異造成的，難以完全根除，但偏差都在一個網格尺度左右，仍顯示出較好的一致性。

2.3 同側和異側激波干擾

對波系較為復雜的多激波干擾問題進行了數值驗證，幾何模型和流場壓強等值線如圖19所示，全場采用均勻的非結構Delaunay三角形網格離散，平均網格尺寸Δ1=0.015L。Ma∞=3.0的高超聲速均勻氣流在經過收縮管道時，經上壁面20°楔角壓縮產生了一道斜激波S1，與此同時，先后經下壁面10°和20°楔角二次壓縮產生了兩道斜激波S2和S3，隨后S2和S3發生了同側正規激波相交并匯聚成了一道新激波S4，最終激波S1與S4發生了異側正規相交并產生了兩條透射激波S5和S6。全場一共產生了六道激波，并存在一個三波點和一個四波點結構。

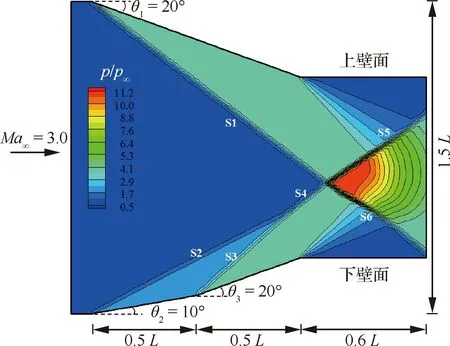
圖19 激波干擾：幾何模型與壓強云圖

根據流向壓強梯度過濾得到的激波帶分布如圖20所示，在兩個激波干擾處聚集了大量的激波單元。通過進一步增補原激波帶外緣兩側的空穴單元，優化后的激波帶更加光順。隨后對優化的激波帶進行K-means聚類，結果如圖21(a)所示，在每條激波帶分支中都分布著大量呈串狀依次排列的普通簇，而在分支交匯處卻聚集著若干分叉簇，這些分叉簇都至少與周圍3個簇直接相鄰，因此需要進行簇合并操作。

圖20 激波干擾：辨識出的激波帶

在將某些簇合并后(圖21(b))，清晰地存在兩個較大的分叉簇，分別與周邊3和4個普通簇相鄰，因此其聚類中心可以被視為三波點和四波點位置。最終分別將各個分支中的聚類中心進行擬合得到了所有6條激波線，結果如圖22所示。擬合的激波線、激波相交點均落在數值捕捉激波的過渡區內，顯示出該算法良好的精度。

圖22 激波干擾：擬合的激波線

實際上，激波(尤其是激波-激波干擾點)的探測精度在很大程度上取決于流場的分辨率。也就是說，捕捉得到的激波過渡區寬度越小，越有利于精確探測到激波及其干擾點的位置。下面考察了網格的疏密程度對激波探測的影響。

在其他相同計算條件下，僅僅改變流場網格的尺寸，分別設計疏(Δ2=0.02L)和密(Δ3=0.01L)兩套非結構網格，重新進行流場計算。經激波辨識、聚類分析和簇合并后的結果如圖23所示；網格越稀，劃分的簇越少，且聚類中心兩兩相距越遠。圖24對比了3種網格尺寸下最終擬合出的激波線，可以發現，三者大部分基本完全吻合，但激波干擾點處差異較大。對于同側激波干擾結構，由于三道激波的斜率都比較接近，因此當網格較稀時，數值捕捉激波的過渡區較寬，會造成兩條入射激波帶提前交匯(對比圖23中兩圖可見)，分叉簇的位置會發生較大改變，最終造成了辨識出的三波點位置出現較大差異。另一方面，對于異側激波干擾產生的四波點結構，雖然稀網格對應的分叉簇也較大，但其聚類中心的位置和密網格的結果偏差并不顯著。

圖23 激波干擾：不同網格尺寸下的聚類結果

圖24 激波干擾：3種網格尺寸下擬合的激波線對比

該算例表明，本文算法對同側激波干擾點的識別精度網格依賴性相對較強，即網格疏密對結果的影響較大；而對于異側激波干擾點，包括上文激波反射算例中的三波點結構，其識別精度受網格尺度的影響較小；而對于干擾點以外的激波線，擬合精度受網格尺度的影響最小，始終吻合得比較好。

2.4 前向臺階非定常流動

采用著名的前向臺階超聲速繞流算例[24]測試該算法在復雜非定常流動中的有效性。均勻自由來流馬赫數Ma∞=3.0，且初始流場取來流參數，通道入口和出口處的高度分別為L和0.8L，臺階高度及其上表面長度分別為0.2L和2.4L。全場采用均勻非結構三角形網格劃分，網格尺度為0.01L。本算例中的時間均為無量綱量。

在流場的發展歷程中，臺階前首先出現一道向左運動的弓形激波，因其強度較大，當受到上壁面干擾時會發生反射，并從運動正規反射逐漸過渡到馬赫反射；而反射激波又從下壁面反射回上壁面，最終在管道壁面形成了4次激波-壁面干擾(Shock-Wall Interaction，SWI)。此外，氣流在臺階拐角處發生過度膨脹，過膨脹氣流會與下壁面相撞形成一道相對較弱的孤立斜激波，該激波最終與第一道反射激波發生異側正規相交，相交后的弱激波又與第二道反射激波匯聚形成同側激波-激波干擾(Shock-Shock Interaction，SSI)結構。

圖25依次給出了5個關鍵時刻的辨識激波帶的聚類結果，通過二次濾波，在辨識出運動強激波的同時，那道較弱的孤立斜激波也被很好地提取出來；此外，圖25(d)和25(e)中并沒有錯誤地將三波點處的接觸間斷提取出來。隨后，通過聚類分析和簇合并操作，可以準確地定位分叉簇與邊界簇的位置，從而清晰地識別出各個時刻流場激波的總個數及相互干擾的模式(如SWI或SSI)。

圖25 前向臺階繞流：不同時刻激波帶的聚類結果

以兩時刻為例，圖26定性比較了最終擬合出的激波線與流場壓強云圖。可以發現，不僅各條近似直線的反射激波位置準確，而且臺階前的大曲率弓形激波也與捕捉激波吻合得很好，反映了該算法對各種形狀激波的擬合都具有較好的可靠性。在得到不同時刻的擬合激波線后，可以方便地將其在同一張圖中顯示出來，進而有利于分析激波的演化過程，深化對運動激波干擾的認識。從圖27可以看出，相比激波-上壁面干擾點，臺階后的激波-下壁面干擾點向左移動的速度更快；且弓形激波在上壁面反射形成的馬赫干擾的長度在迅速增大；而在t=1.5時刻后，弓形激波的位置變化比較緩慢，三波點近似沿弓形激波向下滑動。